DFS算法系列 回溯
DFS算法系列-回溯
文章目录
- DFS算法系列-回溯
- 1. 算法介绍
- 2. 算法应用
- 2.1 全排列
- 2.2 组合
- 2.3 子集
- 3. 总结
1. 算法介绍
回溯算法是一种经典的递归算法,通常被用来解决排列问题、组合问题和搜索问题
基本思想
从一个初始状态开始,按一定的规则向前搜索,当搜索遇到瓶颈无法再前进时,回到当前状态的上一个状态,按照新的要求/条件继续向前搜索,直至所有可用条件都遍历完成。
简单的说就是:不撞南墙不回头
对于回溯算法,其核心就在于不断的"试错",若选择正确则继续往下搜索,否则就"回头"选择另一个选项继续往下搜索。
下面提供一个回溯算法的模板(模板只是对算法理解的总结概况,相较于没有思考的套模板,理解其中的算法思想更加重要–>通过做题积累)
List<List<Integer>> ret;
List<Integer> path; void dfs(int[] nums, ...) {// 满⾜结束条件if (/* 满⾜结束条件 */) {// 将路径添加到结果集中ret.add(new ArrayList<>(path));return;}// 遍历所有选择for (int i = 0;i < nums.size();i++) {// 做出选择path.add(nums[i]); // 做出当前选择后继续搜索dfs(path, nums);// 恢复现场path.remove(path.size() - 1);}
}
其中path用来记录每次选择后改变的路径,nums[i]表示当前做出的选择,并且在当前选择满足递归结束条件后,将当前路径添加到结果集中,结束当前层递归并恢复现场,即恢复刚刚完成修改的路径到上一个状态,才能继续处理当前层的另一个选择,如下图所示:

了解完回溯算法,我们来做一些相关的算法题加深印象!
2. 算法应用
对于回溯(以及DFS相关的题),建议的解题步骤:
- 先画决策树;
- 根据决策树编写函数体,可设置
全局变量、添加剪枝提高效率; - 找到递归出口
2.1 全排列
题目链接:[全排列]
决策树:

代码示例
class Solution {List<List<Integer>> ret;List<Integer> path;boolean[] check;public List<List<Integer>> permute(int[] nums) {ret = new ArrayList<>();path = new ArrayList<>();check = new boolean[nums.length];dfs(nums);return ret;}void dfs(int[] nums) {if (path.size() == nums.length) {ret.add(new ArrayList(path));return;}for (int i = 0;i < nums.length;i++) { // 这里让i=0,使下一层选项依旧为所有情况(1,2,3,4)if (!check[i]) { // check数组用来记录当前数字是否被使用check[i] = true; path.add(nums[i]); // 将数字添加到路径中dfs(nums);check[i] = false;path.remove(path.size() - 1);}}}
}
2.2 组合
题目链接:[组合]
决策树:

代码示例
class Solution {List<List<Integer>> ret;List<Integer> path;boolean[] check;int len;int pre;public List<List<Integer>> combine(int n, int k) {ret = new ArrayList<>();path = new ArrayList<>();check = new boolean[n + 1];len = k;int[] nums = new int[n + 1];for (int i = 1;i <= n;i++) {nums[i] = i;}dfs(nums, 1);return ret;}public void dfs(int[] nums, int pos) {if (path.size() == len) { // 当路径长度和要求的组合数相等时返回ret.add(new ArrayList<>(path));return;}for (int i = pos;i <= nums.length - 1;i++) { // 这里让i=pos,使下一层选项不会出现当前数字,并且下层选项从pos+1开始if (!check[i]) { path.add(nums[i]); check[i] = true;dfs(nums, i + 1);path.remove(path.size() - 1);check[i] = false;}}}
}
注:这里让i=pos,使下一层选项不会出现当前数字,并且下层选项从pos+1开始;若为i = 0,则使下一层选项依旧为所有情况(1,2,3):

2.3 子集
题目链接:[子集]
决策树:

代码示例
class Solution {static List<List<Integer>> ret;static List<Integer> path;public List<List<Integer>> subsets(int[] nums) {ret = new ArrayList<>();path = new ArrayList<>();dfs(nums, 0);return ret;}public void dfs(int[] nums, int cur) {ret.add(new ArrayList<>(path)); // 此处不设出口目的是将每个节点路径都添加到ret中for (int i = cur;i < nums.length;i++) { // 这里让i=cur,使下一层选项不会出现当前数字,并且下层选项从cur+1开始path.add(nums[i]);dfs(nums, i + 1);path.remove(path.size() - 1); }}
}
3. 总结
总的来说,回溯就是不断的"试错"并回头进行新的选择,和回溯相关的题就要把决策树画出来,通过它来找到我们的递归出口并编写函数体(注意for循环中起始标的使用),注意记得恢复现场哦!
相关文章:

DFS算法系列 回溯
DFS算法系列-回溯 文章目录 DFS算法系列-回溯1. 算法介绍2. 算法应用2.1 全排列2.2 组合2.3 子集 3. 总结 1. 算法介绍 回溯算法是一种经典的递归算法,通常被用来解决排列问题、组合问题和搜索问题 基本思想 从一个初始状态开始,按一定的规则向前搜索&…...
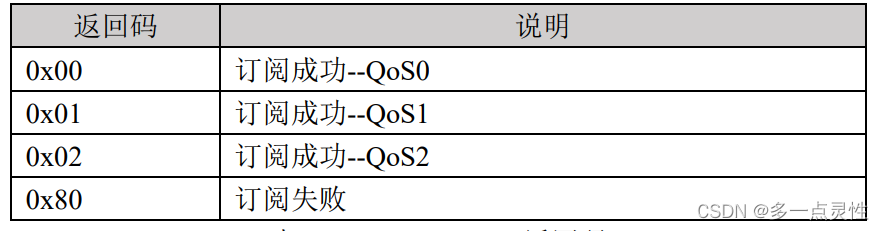
Linux C应用编程:MQTT物联网
1 MQTT通信协议 MQTT(Message Queuing Telemetry Transport,消息队列遥测传 输)是一种基于客户端-服务端架构的消息传输协议,如今,MQTT 成为了最受欢迎的物联网协议,已广泛应用于车联网、智能家居、即时聊…...
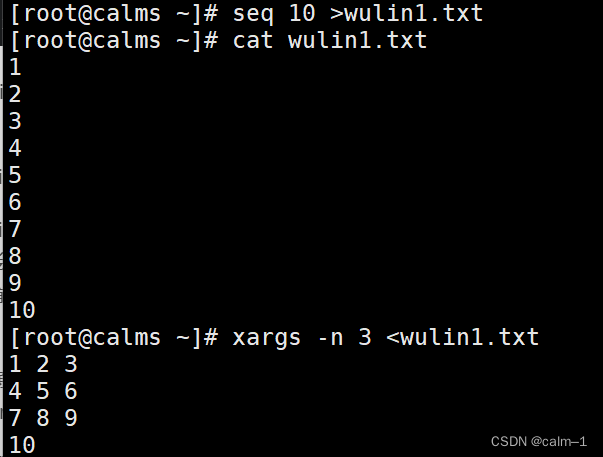
企业常用Linux文件命令相关知识+小案例
远程连接工具无法连接VMWARE: 如果发现连接工具有时连不上,ip存在,这时候我们查看网络编辑器,更多配置,看vnet8是不是10段,nat设置是否是正确的? 软件重启一下虚机还原一下网络编辑器 查看文件…...

Istio介绍
1.什么是Istio Istio是一个开源的服务网格(Service Mesh)框架,它提供了一种简单的方式来为部署在Kubernetes等容器编排平台上的微服务应用添加网络功能。Istio的核心功能包括: 服务治理:Istio能够帮助管理服务之间的…...

代码随想录算法训练营第四十七天|leetcode115、392题
一、leetcode第392题 本题要求判断s是否为t的子序列,因此设置dp数组,dp[i][j]的含义是下标为i-1的子串与下标为j-1的子串相同字符的个数,可得递推公式是通过s[i-1]和t[j-1]是否相等区分。 具体代码如下: class Solution { publ…...

将Ubuntu18.04默认的python3.6升级到python3.8
1、查看现有的 python3 版本 python3 --version 2、安装 python3.8 sudo apt install python3.8 3、将 python3.6 和 3.8 添加到 update-alternatives sudo update-alternatives --install /usr/bin/python3 python3 /usr/bin/python3.6 1 sudo update-alternatives --insta…...
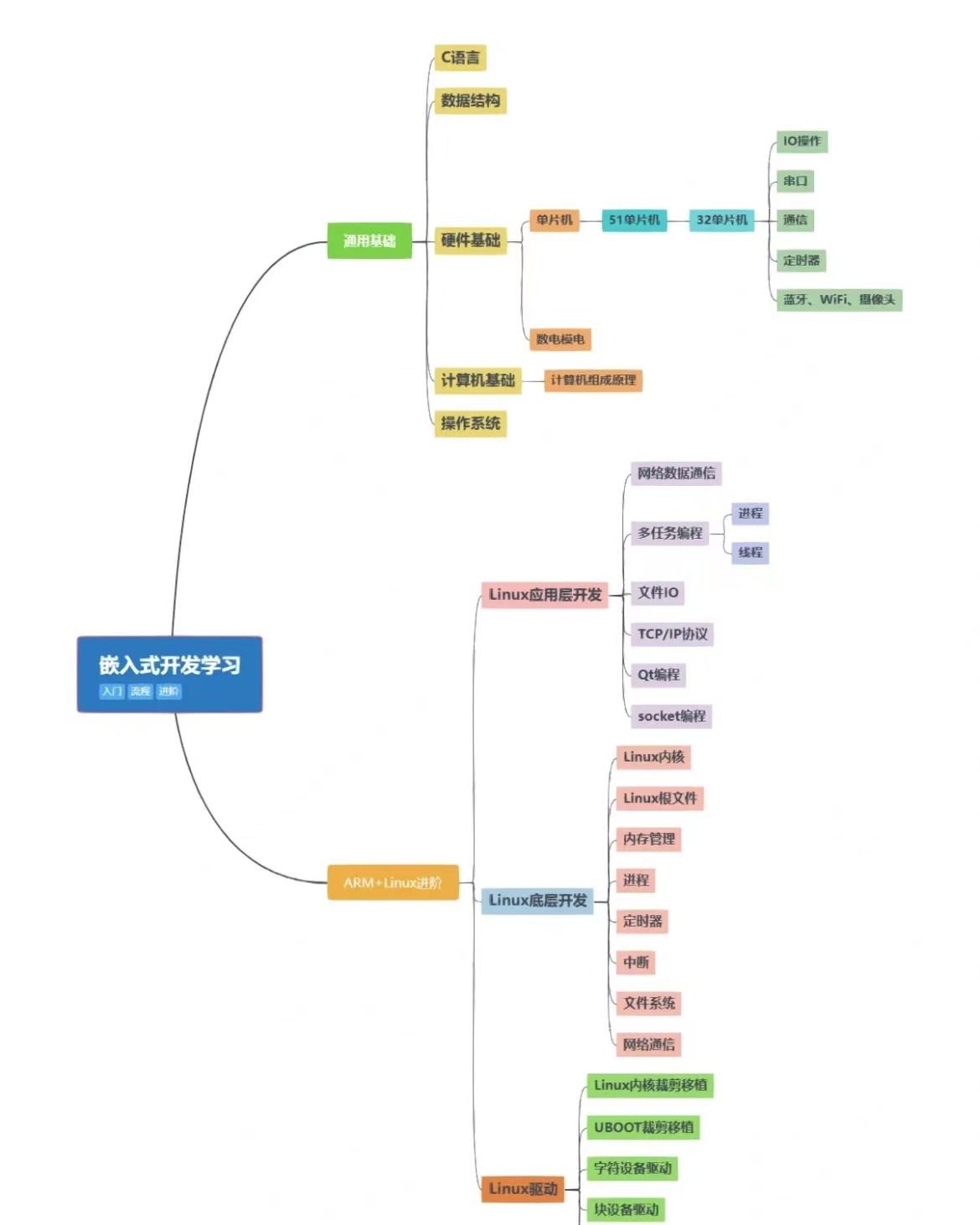
Python和Java哪个更适合后端开发?
Python和Java都是强大的后端开发语言,它们各自有鲜明的特点和适用场景。选择哪一个更适合后端开发,主要取决于具体的项目需求、团队技术栈、个人技能偏好以及长期发展考虑等因素。 下面是两者在后端开发中的优势和劣势: 「Python࿱…...

Python+pytest接口自动化之cookie绕过登录(保持登录状态)
前言 我们今天来聊聊pythonpytest接口自动化之cookie绕过登录(保持登录状态),在编写接口自动化测试用例或其他脚本的过程中,经常会遇到需要绕过用户名/密码或验证码登录,去请求接口的情况,一是因为有时验证…...

什么数据集成(Data Integration):如何将业务数据集成到云平台?
说到数据集成(Data Integration),简单地将所有数据倒入数据湖并不是解决办法。 在这篇文章中,我们将介绍如何轻松集成数据、链接不同来源的数据、将其置于合适的环境中,使其具有相关性并易于使用。 数据集成࿱…...

国外EDM邮件群发多少钱?哪个软件好?
在当今全球化市场环境下,电子邮件营销作为最有效的数字营销渠道之一,其影响力不容忽视。而高效精准的EDM(Electronic Direct Mail)邮件营销策略更是企业拓展海外市场、提升品牌知名度的关键手段。云衔科技以其创新的智能EDM邮件营…...

C语言入门算法——回文数
题目描述: 若一个数(首位不为零)从左向右读与从右向左读都一样,我们就将其称之为回文数。 例如:给定一个十进制数 56,将 56 加 65(即把 56 从右向左读),得到 121 是一个…...

OceanBase—操作实践
文档结构 1、概念简介2、核心设计3、操作实践3.3、数据同步 官方文档:https://www.oceanbase.com/docs/oceanbase-database-cn 1、概念简介 版本分为社区版和企业版,其中企业版兼容MySQL 和Oracle数据库语法; 2、核心设计 存储层 复制层 …...
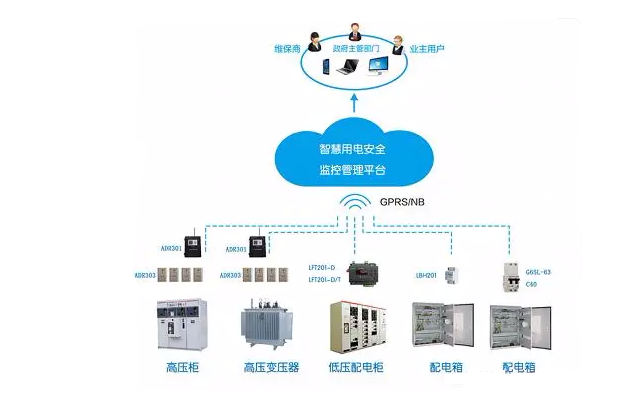
智慧用电安全管理系统
智慧用电安全管理系统 智慧用电安全管理系统是智能电网中客户侧关键的构成部分,是基本建设新型智慧城市的基本,将完成地区内各种各样用电设备的智能化系统监管,完成地区内日常生活与工作中安全性、舒服。 一、智慧用电安全管理系统介绍 …...

Rust语言入门第二篇-Cargo教程
文章目录 Rust语言入门第二篇-Cargo教程一,Cargo 是什么二,Cargo教程Cargo.toml文件src/main.rs 文件构建并运行Cargo项目 Rust语言入门第二篇-Cargo教程 本节提供对cargo命令行工具的快速了解。我们演示了它为我们生成新包的能力,它在包内编…...

测试用例的编写方式
学习目标 能对穷举场景设计测试点能对限定边界规则设计测试点能对多条件依赖关系进行设计测试点能对于项目业务进行设计测试点 目录 等价类划分法案例 等价类划分 说明:在所有测试数据中,具有某种共同特征的数据集合进行划分分类: 有效等…...

HarmonyOS实战开发-状态管理、通过使用页面级的状态变量 和应用级的状态变量 来实现应用的状态管理。
介绍 本示例通过使用页面级的状态变量 和应用级的状态变量 来实现应用的状态管理。 效果预览 使用说明 1.点击首页中的基本类型进入对应页面,点击按钮可以更改圆形的颜色;点击查看源码可以展示基本类型功能效果的源码。 2.点击首页中的数组类型进入对…...

【Java开发指南 | 第二篇】标识符、Java关键字及注释
专栏:Java开发指南 CSDN秋说 文章目录 标识符Java关键字Java注释 标识符 Java 所有的组成部分都需要名字。类名、变量名以及方法名都被称为标识符。 所有的标识符都应该以字母(A-Z 或者 a-z),美元符($)、或者下划线&…...

3D可视化技术:研发基地的科技新篇章
在科技日新月异的今天,我们生活在一个充满无限可能性的时代。而在这个时代中,3D可视化技术正以其独特的魅力,引领着科技领域的新一轮变革。 3D可视化技术通过三维图像的方式,将现实世界或虚拟世界中的物体、场景等以立体、逼真的形…...

蓝旭前端05:JavaScript进阶
蓝旭前端05:JavaScript进阶 基础简单复习 数据类型 基本数据类型:Number、String、Boolean、Null、Undefined等。引用数据类型:Object、Array、Function等。typeof操作符:返回数据类型的字符串形式。 变量 变量声明࿱…...

【docker-compose】安装及配置
目录 安装在线安装离线安装 配置mysql5.7bitnami/mysql8.3redisweb前后台分离部署前端https(SSL)配置nginx动态传参资源限制:内存、cpunacossentinelgateway 问题汇总iptables No chain/target/match by that namedocker-compose.yml修改mysql密码,重启后…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...
