代码随想录算法训练营第五十天|123.买卖股票的最佳时机III 188.买卖股票的最佳时机IV
123.买卖股票的最佳时机III
这道题一下子就难度上来了,关键在于至多买卖两次,这意味着可以买卖一次,可以买卖两次,也可以不买卖。
视频讲解:https://www.bilibili.com/video/BV1WG411K7AR
https://programmercarl.com/0123.%E4%B9%B0%E5%8D%96%E8%82%A1%E7%A5%A8%E7%9A%84%E6%9C%80%E4%BD%B3%E6%97%B6%E6%9C%BAIII.html
题目大意:给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
class Solution {
public:int maxProfit(vector<int>& prices) {if (prices.size() == 0) return 0;vector<vector<int>> dp(prices.size(), vector<int>(5, 0));dp[0][1] = -prices[0];dp[0][3] = -prices[0];for (int i = 1; i < prices.size(); i++) {dp[i][0] = dp[i - 1][0];dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);}return dp[prices.size() - 1][4];}
};
时间复杂度:O(n)
空间复杂度:O(n × 5)
188.买卖股票的最佳时机IV
本题是123.买卖股票的最佳时机III 的进阶版
视频讲解:https://www.bilibili.com/video/BV16M411U7XJ
https://programmercarl.com/0188.%E4%B9%B0%E5%8D%96%E8%82%A1%E7%A5%A8%E7%9A%84%E6%9C%80%E4%BD%B3%E6%97%B6%E6%9C%BAIV.html
题目大意:给定一个整数数组 prices ,它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
class Solution {
public:int maxProfit(int k, vector<int>& prices) {if (prices.size() == 0) return 0;vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));for (int j = 1; j < 2 * k; j += 2) {dp[0][j] = -prices[0];}for (int i = 1;i < prices.size(); i++) {for (int j = 0; j < 2 * k - 1; j += 2) {dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);}}return dp[prices.size() - 1][2 * k];}
};
时间复杂度: O(n * k),其中 n 为 prices 的长度
空间复杂度: O(n * k)
相关文章:

代码随想录算法训练营第五十天|123.买卖股票的最佳时机III 188.买卖股票的最佳时机IV
123.买卖股票的最佳时机III 这道题一下子就难度上来了,关键在于至多买卖两次,这意味着可以买卖一次,可以买卖两次,也可以不买卖。 视频讲解:https://www.bilibili.com/video/BV1WG411K7AR https://programmercarl.com…...
)
Composer安装与配置:简化PHP依赖管理的利器(包括加速镜像设置)
在现代的PHP开发中,我们经常会使用许多第三方库和工具来构建强大的应用程序。然而,手动管理这些依赖项可能会变得复杂和耗时。为了解决这个问题,Composer应运而生。Composer是一个PHP的依赖管理工具,它可以帮助我们轻松地安装、更…...

灯塔:抽象类和接口笔记
什么是构造方法 构造方法是一种特殊的方法,它是一个与类同名且没有返回值类型的方法。 构造方法的功能主要是完成对象的初始化。当类实例化一个对象时会自动调用构造方法,且构造方法和其他方法一样也可以重载 继承抽象类需要实现所有的抽象方法吗 继…...

mybatis 入门
MyBatis是一款持久层框架,免除了几乎所有的JDBC代码、参数及获取结果集工作。可以通过简单的XML或注解来配置和映射原始类型、接口和Java POJO为数据库中的记录。 1 无框架下的JDBC操作 1)加载驱动:Class.forName(“com.mysql.cj.jdbc.Driv…...

Spring-AI-上下文记忆
引入依赖 pom文件 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/P…...

内存函数memcpy、mommove、memset、memcmp
目录 1、memcpy函数 memcpy函数的模拟实现 2、memmove函数 memmove函数的模拟实现 3、memset函数 4、memcmp函数 1、memcpy函数 描述: C 库函数 void *memcpy(void *str1, const void *str2, size_t n) 从存储区 str2 复制 n 个字节到存储区 str1。 声明&…...

symfony框架介绍
Symfony是一个功能强大的PHP框架,它提供了丰富的组件和工具来简化Web开发过程。以下是一些关于Symfony的主要特点: 可重用性: Symfony提供了一系列可重用的PHP组件,这些组件可以用于任何PHP应用程序中。灵活性: Symfony允许开发者根据项目需求灵活选择使用哪些组件,而不是强…...
【计算机毕业设计】游戏售卖网站——后附源码
🎉**欢迎来到琛哥的技术世界!**🎉 📘 博主小档案: 琛哥,一名来自世界500强的资深程序猿,毕业于国内知名985高校。 🔧 技术专长: 琛哥在深度学习任务中展现出卓越的能力&a…...
LabVIEW电信号傅里叶分解合成实验
LabVIEW电信号傅里叶分解合成实验 电信号的分析与处理在科研和工业领域中起着越来越重要的作用。系统以LabVIEW软件为基础,开发了一个集电信号的傅里叶分解、合成、频率响应及频谱分析功能于一体的虚拟仿真实验系统。系统不仅能够模拟实际电路实验箱的全部功能&…...

Docker 学习笔记(六):挑战容器数据卷技术一文通,实战多个 MySQL 数据同步,能懂会用,初学必备
一、前言 记录时间 [2024-4-11] 系列文章简摘: Docker学习笔记(二):在Linux中部署Docker(Centos7下安装docker、环境配置,以及镜像简单使用) Docker 学习笔记(三)&#x…...

csdn怎么变得这么恶心,自动把一些好的文章分享改成了vip可见
刚刚发现以前发的一些文章未经过我同意,被csdn自动改成了VIP可见,这也太恶心了,第一你没分钱给我,第二我记录下一些问题也不是为了赚钱,而是为了提升自己和帮助别人,这样搞是想逼更多人走是吗?...

自然语言处理NLP:文本预处理Text Pre-Processing
大家好,自然语言处理(NLP)是计算机科学领域与人工智能领域中的一个重要方向,其研究能实现人与计算机之间用自然语言进行有效通信的各种理论和方法。本文将介绍文本预处理的本质、原理、应用等内容,助力自然语言处理和模型的生成使用。 1.文本…...
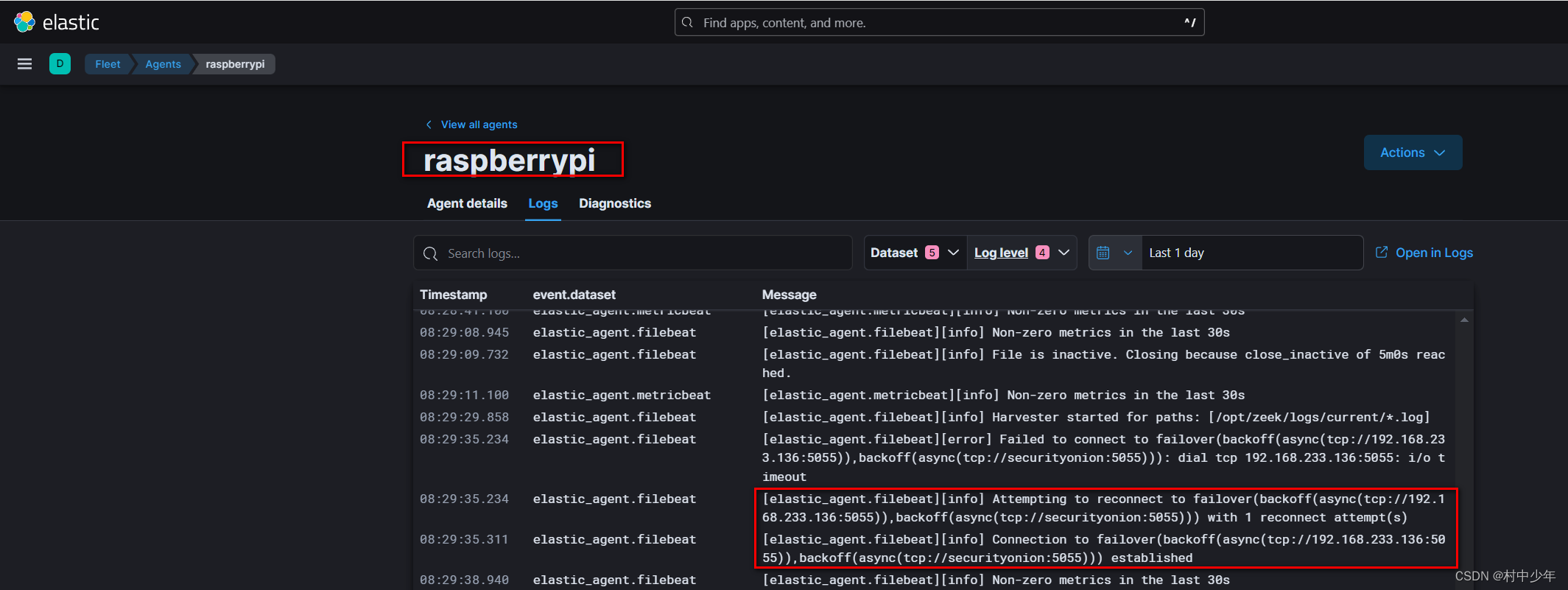
家庭网络防御系统搭建-虚拟机安装siem/securityonion网络连接问题汇总
由于我是在虚拟机中安装的security onion,在此过程中,遇到很多的网络访问不通的问题,通过该文章把网络连接问题做一下梳理。如果直接把securityonion 安装在物理机上,网络问题则会少很多。 NAT无法访问虚拟机 security onion虚拟…...
2024年外贸行业营销神器推荐
2024年外贸行业营销神器推荐:外贸人每天面对的不是国内客户,而是全球客户,相对于国内来说,会更加麻烦和繁琐,今天就码一篇2024年外贸行业营销神器的推荐文章,希望可以减轻各位外贸人的负担! 1、…...

k8s高可用集群部署介绍 -- 理论
部署官网参考文档 负载均衡参考 官网两种部署模式拓扑图和介绍 介绍两种高可用模式 堆叠 拓扑图如下(图片来自k8s官网): 特点:将etcd数据库作为控制平台的一员,由于etcd的共识算法,所以集群最少为3个&…...

【GDAL-Python】1-在Python中使用GDAL读写栅格文件
文章目录 1-概要2.代码实现 1-概要 提示:本教程介绍如何使用 Python 中的 GDAL 库将栅格数据读取为数组并将数组另存为GeoTiff 文件 视频地址:B站对应教程 目标: (1)读写GeoTiff影像; (2&…...

【C++】explicit关键字详解(explicit关键字是什么? 为什么需要explicit关键字? 如何使用explicit 关键字)
目录 一、前言 二、explicit关键字是什么? 三、构造函数还具有类型转换的作用 🍎单参构造函数 ✨引出 explicit 关键字 🍍多参构造函数 ✨为什么需要explicit关键字? ✨怎么使用explicit关键字? 四、总结 五…...
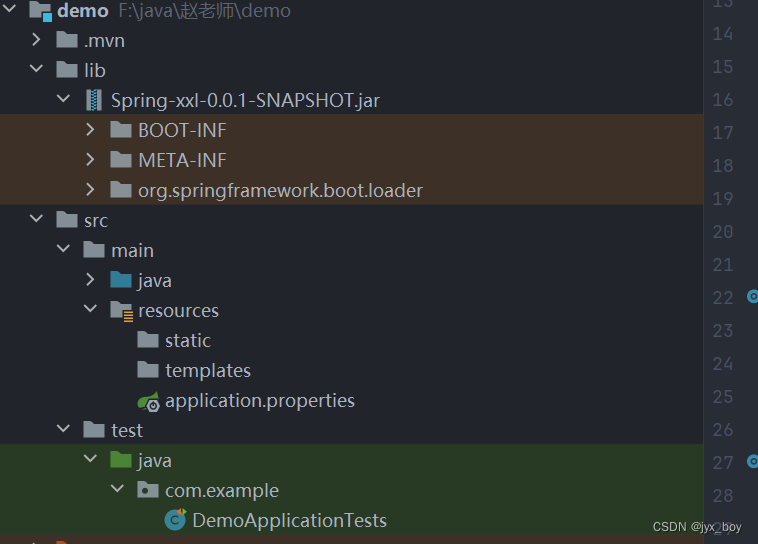
maven引入外部jar包
将jar包放入文件夹lib包中 pom文件 <dependency><groupId>com.jyx</groupId><artifactId>Spring-xxl</artifactId><version>1.0-SNAPSHOT</version><scope>system</scope><systemPath>${project.basedir}/lib/Spr…...

李沐37_微调——自学笔记
标注数据集很贵 网络架构 1.一般神经网络分为两块,一是特征抽取原始像素变成容易线性分割的特征,二是线性分类器来做分类 微调 1.原数据集不能直接使用,因为标号发生改变,通过微调可以仍然对我数据集做特征提取 2.pre-train源…...
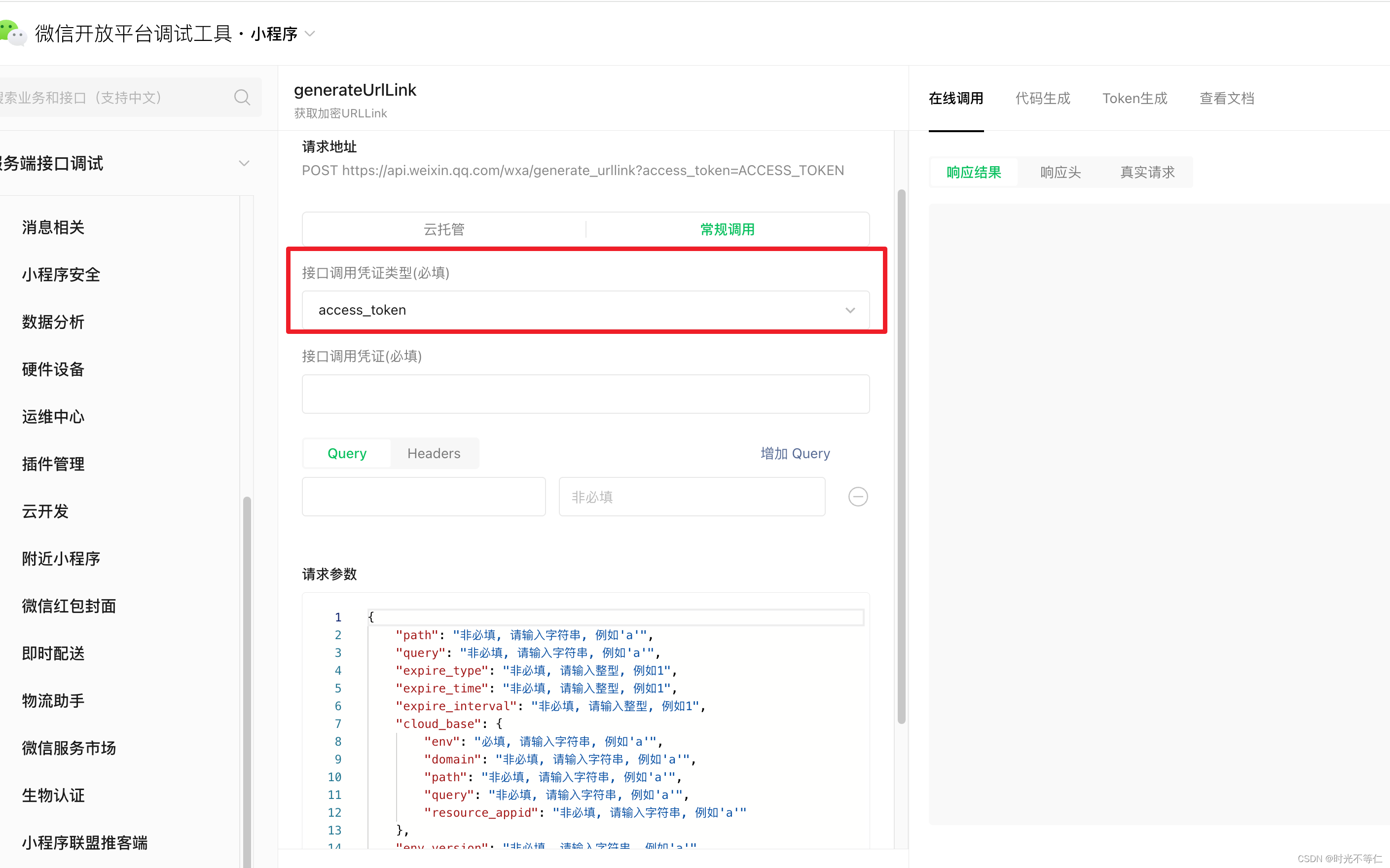
【小程序】生成短信中可点击的链接
文章目录 前言一、如何生成链接二、仔细拜读小程序开发文档文档说明1文档说明2 总结 前言 由于线上运营需求,需要给用户发送炮轰短信,用户通过短信点击链接直接跳转进入小程序 一、如何生成链接 先是找了一些三方的,生成的倒是快速…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...
数据挖掘是什么?数据挖掘技术有哪些?
目录 一、数据挖掘是什么 二、常见的数据挖掘技术 1. 关联规则挖掘 2. 分类算法 3. 聚类分析 4. 回归分析 三、数据挖掘的应用领域 1. 商业领域 2. 医疗领域 3. 金融领域 4. 其他领域 四、数据挖掘面临的挑战和未来趋势 1. 面临的挑战 2. 未来趋势 五、总结 数据…...
