代码随想录算法训练营第四十一天| 343. 整数拆分,96.不同的二叉搜索树
题目与题解
343. 整数拆分
题目链接:343. 整数拆分
代码随想录题解:343. 整数拆分
视频讲解:动态规划,本题关键在于理解递推公式!| LeetCode:343. 整数拆分_哔哩哔哩_bilibili
解题思路:
一眼懵,直接看答案了
看完代码随想录之后的想法
前一天的题是由dp[i-2]和dp[i-1],递推出当前结果dp[i]。这题更复杂一些,是要根据dp[0]到dp[i-1],推算dp[i]的结果。
对于数字i,可以分解为两个数字的和:j和i-j,因此求分解i的乘积,就是求j和分解i-j之后二者的乘积。那么如果dp[i]定义为数字i的最大乘积和,那么对于dp[i],遍历j from 1 to i - 1, 递推公式为求dp[i-j]*j和j * (i - j) 中的最大值。
为避免重复计算,j最多取到i的一半。
class Solution {public int integerBreak(int n) {int[] dp = new int[n+1];if (n >= 2) dp[2] = 1;for (int i = 3; i <= n; i++) {for (int j = 1; j <= i/2; j++) {dp[i] = Math.max(dp[i], Math.max(j*(i-j), dp[i-j]*j));}}return dp[n];}
}j怎么就不拆分呢?
j是从1开始遍历,拆分j的情况,在遍历j的过程中其实都计算过了。那么从1遍历j,比较(i - j) * j和dp[i - j] * j 取最大的。递推公式:dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
也可以这么理解,j * (i - j) 是单纯的把整数拆分为两个数相乘,而j * dp[i - j]是拆分成两个以及两个以上的个数相乘。
如果定义dp[i - j] * dp[j] 也是默认将一个数强制拆成4份以及4份以上了。
所以递推公式:dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j});
还需要注意,初始化的方式是跟着定义走的,如果求的是max(dp[i - j] * dp[j]),为了计算正确,初始化的结果会跟dp[i]定义不符,容易出错。
遇到的困难
第一次碰到这种题,想不到
96.不同的二叉搜索树
题目链接:96.不同的二叉搜索树
代码随想录题解:96.不同的二叉搜索树
视频讲解:动态规划找到子状态之间的关系很重要!| LeetCode:96.不同的二叉搜索树_哔哩哔哩_bilibili
解题思路:
这题跟上面一题有一点类似,同样是要用多个dp[i-j]的值推出dp[i]。
题目要求用1-n的数字构成不同的二叉搜索树,其实可以分解为,0-j-1的数字构成左子树,j为根节点,j到i构成右子树,那么
初始化dp[0]=dp[1]=0即可。
class Solution {public int numTrees(int n) {int[] dp = new int[n+1];dp[0] = 1;dp[1] = 1;for (int i = 2; i <= n; i++) {for (int j = 1; j <= i ; j++) {dp[i] += dp[j-1] * dp[i-j];}}return dp[n];}
}看完代码随想录之后的想法
以dp[3]为例
dp[3],就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量
元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量
关键是看如何去分解,分解后如何正确确定遍历的上下限。
遇到的困难
一开始写的时候没有想清楚遍历的边界,初始化的时候也有点糊涂,所以错了好几处。要记住按定义初始化dp,然后确定遍历上下界后,最好通过几个举例得到结果,保证边界正确。
今日收获
学会了如何用分解的方法使用dp,难度提升了很多。
相关文章:
代码随想录算法训练营第四十一天| 343. 整数拆分,96.不同的二叉搜索树
题目与题解 343. 整数拆分 题目链接:343. 整数拆分 代码随想录题解:343. 整数拆分 视频讲解:动态规划,本题关键在于理解递推公式!| LeetCode:343. 整数拆分_哔哩哔哩_bilibili 解题思路: 一眼懵…...
【MATLAB源码-第53期】m代码基于粒子群算法(PSO)的三维路径规划,显示最优路径和适应度曲线。
操作环境: MATLAB 2022a 1、算法描述 粒子群算法(Particle Swarm Optimization,简称PSO)是一种模拟鸟群觅食行为的启发式优化方法。以下是其详细描述: 基本思想: 鸟群在寻找食物时,每只鸟都…...

el-table多行合并
背景 前端统计列表,数据乱序。按日期、产品、阶段、DD项(所有header名称乱写)排序,列表如下。 示例 日期产品阶段DDEEFFGG20240414产品1阶段1场景1A01场景2B01其他A0120240410产品1阶段1场景2B01其他A0120240402产品2阶段1场景3…...

Vue3 + Element-Plus 使用 Table 插槽时数据未及时更新
Vue3 Element-Plus 使用 Table 插槽时数据未及时更新 问题重现解决方法最终效果 问题重现 这里我已经通过二级分类 id 查询到一级分类和二级分类,但是使用插槽和 v-for 渲染出来还是之前的分类 id,但是一点击表格或者保存代码他又能正常刷新出来。 <…...

vue 2 怎么把2024-04-13T17:42:19转换成短日期格式
我们在日常开发过程中,通常会将日期格式在entity中设置成LocalDateTime。这样就有一个麻烦,我们在前端展示这个日期的时候就会变成2024-04-13T17:42:19。这显然不是我们所要的效果,所以我们今天来解决这个问题,让前端展示正确的日…...
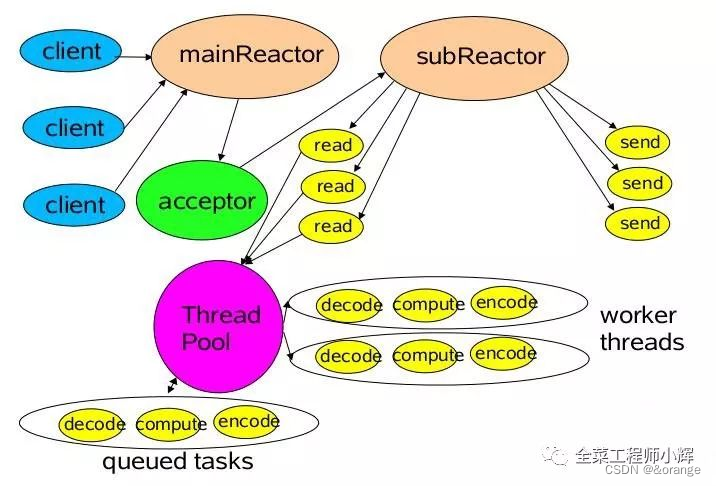
网络IO模型以及实际应用
网络IO模型 本文主要介绍了几种不同的网络IO模型,以及实际应用中使用到的Reactor模型等。 我们常说的网络IO模型,主要包含阻塞IO、非阻塞IO、多路复用IO、信号驱动IO、异步IO。 根据第一个阶段:是否需要阻塞,分为阻塞和非阻塞IO。…...
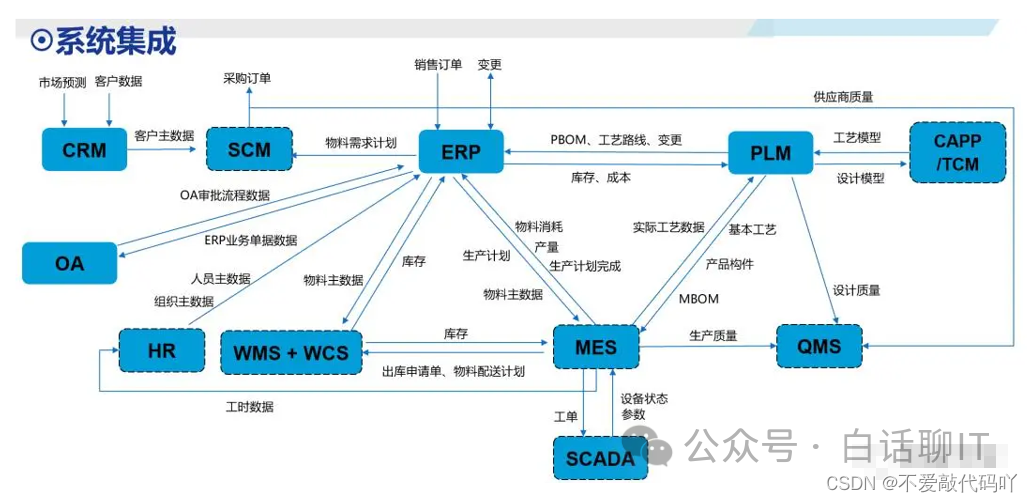
一文详解MES、ERP、SCM、WMS、APS、SCADA、PLM、QMS、CRM、EAM及其关系
经常遇到很多系统,比如:MES、ERP、SCM、WMS、APS、SCADA、PLM、QMS、CRM、EAM,这些都是什么系统?有什么功能和作用?它们之间的关系是怎样的? 今天就一文详细分享给大家。 10大系统之间的关系 ERP 和其他…...

《Kubernetes部署篇:基于Kylin V10+ARM架构CPU使用containerd部署K8S 1.26.15集群(一主多从)》
总结:整理不易,如果对你有帮助,可否点赞关注一下? 更多详细内容请参考:企业级K8s集群运维实战 1、在当前实验环境中安装K8S1.25.14版本,出现了一个问题,就是在pod中访问百度网站,大概时间有10s多,这个时间太长了,尝试了各种办法,都解决不了,后面尝试安装了了1.26.…...

maven命令
mvn archetype:generate 创建 Maven 项目 mvn compile 编译源代码 mvn deploy 发布项目 mvn test-compile 编译测试源代码 mvn test 运行应用程序中的单元测试 mvn site 生成项目相关信息的网站 mvn clean 清除项目目录中的生成结果 mvn package 根据项目生成的 jar mvn instal…...
jetson系列开发板使用虚拟机烧录系统时,遇见无法识别开发板的情况
在双系统中的ubuntu系统烧录没问题,但是电脑Ubuntu系统由于版本低,所以没有网络,烧录起来还的连网线,所以问了开发板的工程师,所幸,解决了问题,很感谢工程师的指导,特此记录一下&…...
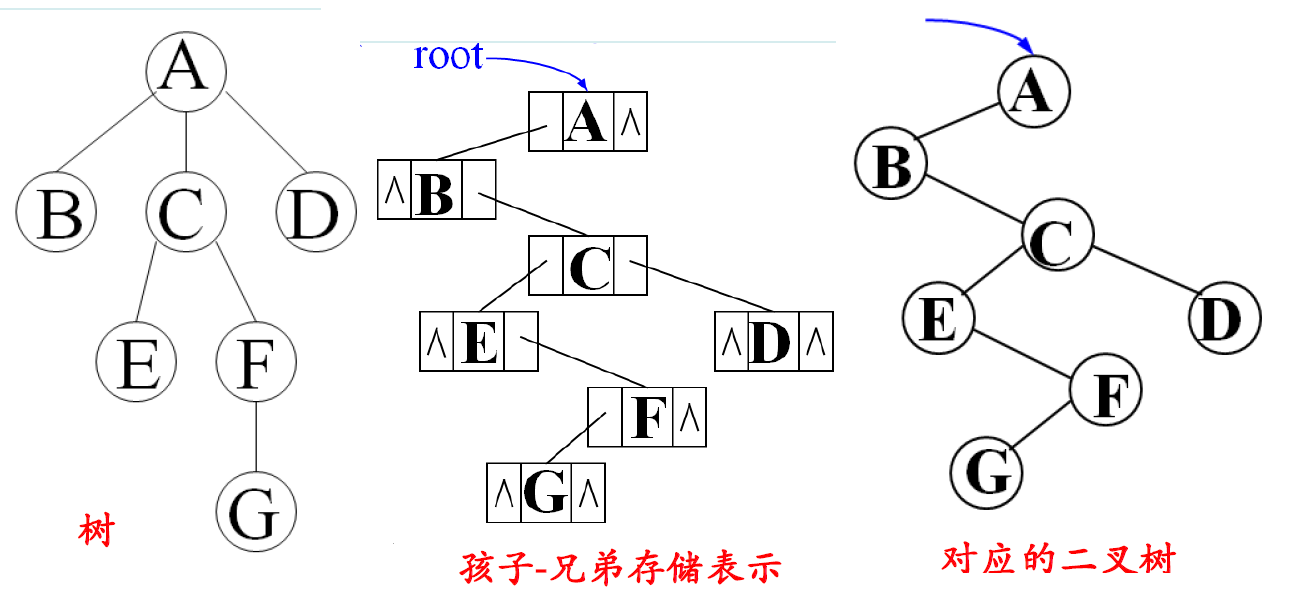
【数据结构】树与二叉树、树与森林部分习题以及算法设计例题 2
目录 【数据结构】树与二叉树、树与森林部分习题以及算法设计例题一、交换二叉树每个结点的左右孩子Swap 函数(先序遍历):Swap 函数(中序遍历) 不可行:Swap 函数(后序遍历)ÿ…...

Cesium之home键开关及相机位置设置
显隐控制 设置代码中的homeButton var TDT_IMG_C "https://{s}.tianditu.gov.cn/img_c/wmts?servicewmts&requestGetTile&version1.0.0" "&LAYERimg&tileMatrixSetc&TileMatrix{TileMatrix}&TileRow{TileRow}&TileCol{TileCol}…...
FreeRTOS_day1
1.总结keil5下载代码和编译代码需要注意的事项 下载代码前要对仿真进行设置 勾选后代码会立刻执行 勾选后会导致代码不能执行 写代码的时候要写在对应的begin和end之间,否则会被覆盖 2.总结STM32Cubemx的使用方法和需要注意的事项 ①打开软件,新建工程…...

Nginx日志格式化和追踪
背景 Nginx是一款功能强大的Web服务器,对于网络环境中的日志记录和配置至关重要。定制化Nginx日志格式可以帮助管理员更好地监控服务器性能、分析用户行为并做出相应优化。在本文中,我们将深入探讨Nginx日志格式的高级定制化策略,包括理解基…...

华为交换机配置telnet SSH登录步骤
这次项目中的交换机是华为 S5735-L24T4X 需要配置telnet和 SSH登录 在平时项目中发现,华为不同型号,不同版本的配置命令也是不同,(这不是脑子有问题吗? 干啥搞成不一样的) 本次型号:S5735-L2…...

市面上加密混淆软件的比较和推荐
引言 市面上有许多加密混淆软件可供开发者使用,但哪些软件是最好用的?哪些软件受到开发者的喜爱?本文将根据一次在CSDN上的投票结果,为大家介绍几款在程序员中普及度较高的加密软件。以下是投票结果,希望能对大家的选择…...

最新AI创作系统ChatGPT网站源码AI绘画,GPTs,AI换脸支持,GPT联网提问、DALL-E3文生图
一、前言 SparkAi创作系统是基于ChatGPT进行开发的Ai智能问答系统和Midjourney绘画系统,支持OpenAI-GPT全模型国内AI全模型。本期针对源码系统整体测试下来非常完美,那么如何搭建部署AI创作ChatGPT?小编这里写一个详细图文教程吧。已支持GPT…...

电视盒子哪个好?2024口碑网络电视盒子排行榜
多年来电视盒子始终占据重要地位,功能上并没有受到影响。在这么多品牌中哪些电视盒子的评价是最好的呢?小编根据各大电商平台的用户评价情况整理了口碑最好的网络电视盒子排行榜,跟着小编一起看看市面上的电视盒子哪个好吧。 TOP 1࿱…...

CookieSession
目录 什么是会话 一.Cookie 1.Cookie介绍 2.Cookie的作用 3.Cookie的基本使用 4.Cookie生命周期 5.Cookie有效路径 6.注意事项 二.Session 1.Session基本原理 2 Session的作用 3.Session的基本使用 4.Session底层实现机制 5.Session生命周期 什么是会话 Cookie和S…...
Nginx服务 重写功能与反向代理
六、重写功能 rewrite Nginx服务器利用 ngx_http_rewrite_module 模块解析和处理rewrite请求,此功能依靠 PCRE(perl compatible regular expression),因此编译之前要安装PCRE库,rewrite是nginx服务器的重要功能之一,用于实现URL的…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...
