致敬我的C++启蒙老师,跟着他学计算机编程就对了 (文末赠书5本)
致敬我的C++启蒙老师,跟着他学计算机编程就对了
摘要
讲述了一个故事,介绍了一位良师,一段因C++而续写的回忆,希望对各位看官有所帮助和启发。
文章目录
- 1 写在前面
- 2 我的C++启蒙老师
- 3 谈谈老师给我的启发
- 4 友情推荐
- 5 文末福利
1 写在前面
写这篇文章,其实是源于前些天我在C站认识了一个我在深大的师弟:曹无悔的博客_CSDN博客-深圳大学,算法与数据结构,C++程序设计领域博主
我也是无意中刷到他的,我印象中好像是在C站的blink里面刷到的,看到他的很多文章开头都是:深圳大学 xxx,这一下子就吸引了我的注意力。
其实我挺喜欢这种标题风格的,之前我也是偏向于这种风格,但是目前碍于流量,还是做了部分妥协,标题还是有些修饰的成分在里面。
聊到学校的师弟,自然勾起了不少在校时的回忆,仔细一想都已经过去10年+了。
看到师弟的博文,我一猜就是深大 计院 的,这让我想起了我在校的C++启蒙老师:深圳大学杜老师。
2 我的C++启蒙老师
聊起我的C++启蒙老师杜老师,必须要重起一个章节来重点讲一讲。
早前,我在某一篇文章中提及过,我在学校时学习C++的苦与泪,感兴趣的可以看看我这篇博文:含泪吐槽学C++的血与泪_架构师李肯的博客-CSDN博客
虽说当时学习C++,真的是脑子进水了,稀里糊涂因为崇拜杜老师就选上这门课了,尽管最后该门课的期末考试也不是很理想,但我觉得能从打心底里佩服一位老师,然后摆在他门下学习专业知识,我个人认为这是一种享受。
你崇拜一位老师,不单单可能是冲着他的专业技术,还可能是他待人处事,教风教纪等非专业的领域的某些亮点打动了你。而我这位杜老师,却是这亮点均占了,这也是我为何冒着挂科的危险,当时也义无反顾地选修了本不该我选修的C++课程。
3 谈谈老师给我的启发
上面也说了,对于杜老师,我是真的很崇拜的,其实主要也是上面提交的两点:
- 专业知识够硬,能够在深大做到计算机软件学院副教授的位置,必须是有两把刷子的;当年给我们这群大一的小白上《大学生计算机基础教程》时,吹下的牛逼:《就这一页PPT,我要是跟你讲起来,可以讲一天》。好吧,有这个实力,才敢说出这样的话。
- 时间理论哲学家,这是他从非技术领域打动我的一点,我印象很清楚,他在课上跟我们讲过一句话叫:“时间总是会过去的!” 我那时候基本都把这句话当座右铭了。理解起来也很简单,读大学那会,其实很多同学都是在虚度光阴,成天窝在宿舍打游戏,就算去上课了,也只是换个地方睡觉而已。而杜老师对这种态度的学生是非常痛斥的,于是就是有了前面那句话。一天的时间都是24小时,无论你选择学习,还是打游戏,它总是会过去的;而学到的东西终究全是你的,别人一点都抢不走。
当然,上面的时间理论,在大学那会我还用在非学习领域,比如遇到了一些很烦心、很痛苦的事,我也会这样来安慰自己,时间总是会过去的,慢慢地时间久了,也就不去想,也就不会痛了。
这个的确有点哲学的味道在里面。
4 友情推荐
回到之前跟师弟的聊天,我本来想问他有没有上过杜老师的课的,结果他说他选修的是另一位老师,然后他告诉我杜老师在B站讲课很火,这让我太惊讶了。
这次趁着有空,我感觉去B站找了一下他,由于我并没有问师弟老师的B站名称是什么,我只能尝试 C++、杜老师、**深大(深圳大学)**等字眼去查找,没想到真的被找到了。
在这里正是推荐一下,杜老师的B站:深圳大学杜老师
以下就是入驻B站的副教授杜老师,这么子说吧,跟着他学计算机编程,绝对没错。相信我,这可不是外部XXX培训班的讲课老师能比的。
对杜老师的视频感兴趣的,别忘了给他点个赞哦。
5 文末福利
为了应景,特意为了回馈粉丝朋友,搞了几本C++的专业书籍来,老规矩,戳这里到我的技术社区,了解赠书活动吧。

相关文章:

致敬我的C++启蒙老师,跟着他学计算机编程就对了 (文末赠书5本)
致敬我的C启蒙老师,跟着他学计算机编程就对了 摘要 讲述了一个故事,介绍了一位良师,一段因C而续写的回忆,希望对各位看官有所帮助和启发。 文章目录1 写在前面2 我的C启蒙老师3 谈谈老师给我的启发4 友情推荐5 文末福利1 写在前面…...

CSS中的伪元素和伪类
一直被伪类和伪元素所迷惑,以为是同一个属性名称,根据CSS动画,索性开始研究a:hover:after,a.hover:after的用法。 伪元素 是HTML中并不存在的元素,用于将特殊的效果添加到某些选择器。 对伪元素的描述 伪元素有两…...

逻辑优化基础-rewrite
简介 逻辑综合中的rewrite算法是一种常见的优化算法,其主要作用是通过对逻辑电路的布尔函数进行等效变换,从而达到优化电路面积、时序和功耗等目的。本文将对rewrite算法进行详细介绍,并附带Verilog代码示例。 一、算法原理 rewrite算法的…...
案例27-单表从9个更新语句调整为2个
目录 一:背景介绍 二:思路&方案 三:过程 1.项目结构 2.准备一个普通的maven项目,部署好mysql数据库 3.在项目中引入pom依赖 5.编写MyBitis配置文件 6.编写Mysql配置类 7.编写通用Update语句 8.项目启动类 四:总…...

Wordpress paid-memberships-pro plugins CVE-2023-23488未授权SQLi漏洞分析
目录 1.漏洞概述 2.漏洞等级 3.调试环境 4.漏洞代码 5 POC 1.漏洞概述 WordPress插件paid-memberships-pro版本<2.9.8中,容易受到REST路由“/pmpro/v1/order”的“code”参数中未验证的SQL注入漏洞的影响。攻击者可进行SQLi盲注,从而获取数据库权限。 CVE:...

【JavaWeb篇】JSTL相关知识点总结
目录 为什么会有JSTL? 什么是JSTL? 如何理解JSTL标准标签库呢? 如何使用JSTL? 第一步:引入JSTL标签库对应的jar包。 第二步:在JSP中引入要使用标签库。(使用taglib指令引入标签库。&#x…...

【蓝桥杯刷题】坑爹的负进制转换
【蓝桥杯刷题】——坑爹的负进制转换😎😎😎 目录 💡前言🌞: 💛坑爹的负进制转换题目💛 💪 解题思路的分享💪 😊题目源码的分享Ƕ…...

react+antdpro+ts实现企业级项目二:Strapi及认证登陆模块
在上一章节中,我们已经成功创建并登陆了系统,现在需要为系统添加权限和登录认证,以提高系统的安全性、数据保护、个性化服务和用户体验。此外,添加权限和登录认证还可以方便管理员进行用户和授权管理。为了快速开发前端࿰…...

Android ANR trace日志如何导出
什么是ANR ?上网搜索,一搜一大片,我就说个很容易识别的字眼,XXXAPP无响应 ANR trace日志如何导出?使用ADB命令: adb pull data/anr/trace.txt 你要存放的路径。查看ANR报错位置全局搜索你APP的包名&#x…...

Windows SSH 配置和SCP的使用
使用用户界面安装 ssh 功能 要在 Windows 10/11 上启用 SSH 服务器,请按照以下步骤操作: 按“Windows 键 I”打开“设置”菜单,然后选择“应用程序”。在左侧菜单栏中选择“应用和功能”。从列表中选择“可选功能”。 点击“添加功能”按钮…...

liunx 安装redsi和连接
liunx 安装redsi和连接 下载 (https://download.redis.io/releases/) 上传到 /usr/local目录 解压 tar -xvf redis-5.0.14.tar.gz 切换到 cd ./redis-5.0.14 编译 make 安装 make install 默认安装目录 /usr/local/bin/ 修改 ./redis-5.0.14/reds…...
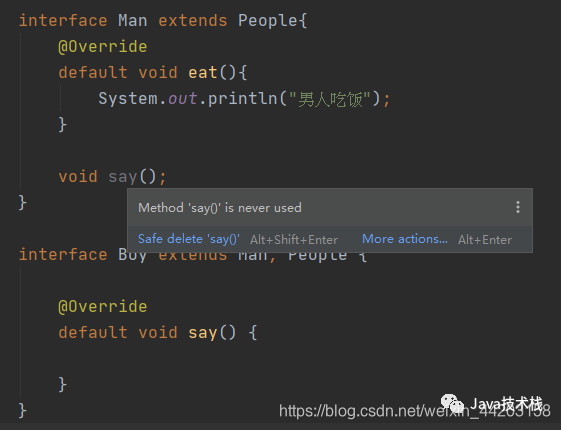
接口里面可以写实现方法吗【可以】 、接口可以多继承吗【可以】
比如下面这道题: 问: 接口里面可以写方法吗? 答: 当然可以啊,默认就是抽象方法。 . 问: 那接口里面可以写实现方法吗? 答: 不可以,所有方法必须是抽象的。 . 问: 你确定吗࿱…...
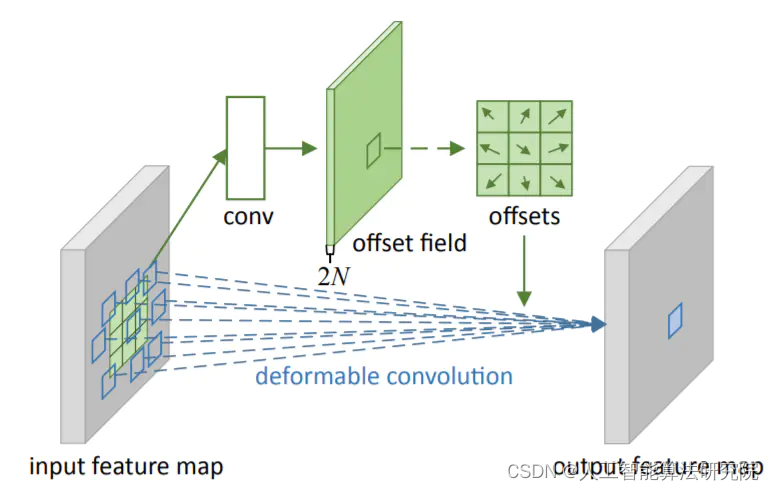
【YOLOv8/YOLOv7/YOLOv5/YOLOv4/Faster-rcnn系列算法改进NO.57】引入可形变卷积
文章目录前言一、解决问题二、基本原理三、添加方法四、总结前言 作为当前先进的深度学习目标检测算法YOLOv8,已经集合了大量的trick,但是还是有提高和改进的空间,针对具体应用场景下的检测难点,可以不同的改进方法。此后的系列…...
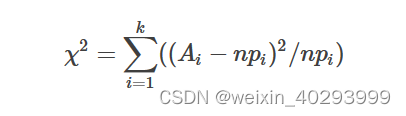
统计学习--三种常见的相关系数
1)Pearson积差相关系数:用于量度两个变量X和Y之间的线性相关。它具有1和-1之间的值,其中1是总正线性相关性,0是非线性相关性,并且-1是总负线性相关性。Pearson相关系数的一个关键数学特性是它在两个变量的位置和尺度的…...
基于Django4.1.4的入门学习记录
基于Django4.1.4的入门学习记录Django创建Django项目创建工程工程目录说明运行开发服务器settings.py配置文件应用的创建创建应用模块应用模块文件说明App应用配置注册安装子应用数据模型ORM概述定义模型类生成数据库表查看数据库文件Admin管理工具管理界面本地化创建管理员注册…...

C++ Butterworth N阶滤波器设计
介绍一个 Butterworth Nth 滤波器设计系数的函数,像 Matlab 函数一样的: [bl,al]butter(but_order,Ws); 和 [bh,ah]butter(but_order,2*bandwidth(1)/fs,high);rtfilter 在 Ububtu 中,容易找到: $ aptitude search ~dbutterwo…...

UXP下不用任何框架创建自己的插件并试运行
在上一篇文章中《Windows下vue框架下的UXP插件开发环境搭建及程序试运行》,搭建的是利用vue框架进行开发的UXP开发环境,而且是把官方的案例插件直接添加进UDT,下面要说的是不利用任何js的框架创建和试运行自己的UXP插件程序,这样来…...

mac修改国内源快速安装brew
我是参考了清华源官网,有任何困惑直接访问该网址即可。这里给出精简版。 1. 更改镜像到~/.zshrc 终端添加方式 echo export HOMEBREW_API_DOMAIN"https://mirrors.tuna.tsinghua.edu.cn/homebrew-bottles/api" >> ~/.zshrcecho export HOMEBREW_…...

Me-and-My-Girlfriend-1靶场通关
Me-and-My-Girlfriend-1靶场通关 靶机ip:192.168.112.135 信息收集 端口:22、80 还是从80WEB服务器端口入手 对服务器目录进行扫描,扫出以下目录 访问80端口WEB服务,显示一段文字只允许本地用户访问。 一眼伪造ip,查看页面…...

2.6 棋盘覆盖
在一个2*x2‘个方格组成的棋盘中,若怡有一个方格与其他方格不同,则称该方格为特殊方格,且称该棋盘为一特殊棋盘。显然,特殊方格在棋盘上出现的位置有 4种情形因而对任何k0,有4‘种特殊棋盘。图2-4 申的特殊棋益是12时 …...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
