2.6 棋盘覆盖

在一个2*x2‘个方格组成的棋盘中,若怡有一个方格与其他方格不同,则称该方格为
特殊方格,且称该棋盘为一特殊棋盘。显然,特殊方格在棋盘上出现的位置有 4种情形
因而对任何k=0,有4‘种特殊棋盘。图2-4 申的特殊棋益是1=2时 16个特殊棋盘中的一个
在棋盘複盖问题中,要用图2-5 所示的 4种不同形态的工 型骨牌覆盖一个给定的特殊棋
盘上除特殊方格以外的所有方格,且任何 2 个 L 型骨牌不得重叠覆盖。易知,在任何一个
2*x2*的棋盘覆盖中,用到的L 型骨牌个数恰为(45-1)/3。

用分治策咯,可以设计解棋盘復盖问题的一个简捷的算法。当心0时,将2'x2*棋盛分
割为 4个25-x25!子棋盛,如图 2-6(a)所示。特殊方格必位于 4 个较小子棋盘之一中,其余3
个子棋盘中无特殊方格。为了将这 了个无特殊方格的子棋盘转化为特殊棋盘,可以用一个山
型骨牌覆盖这了个较小棋盘的会合处,如图2-6(所示,这了个子棋盘上被L型骨牌覆盖的方
格就成为该棋盘上的特殊方格,从而将原问题转化为 4个较小规模的棋盘覆盖问题。递归地使用
这种分割,直至棋盘简化为 1×1 棋盘。
实现这种分治策略的算法 Chess Board 如下:
void ChessBoard (int tr, int tc, int dr, int dc, int size) {
if (size ==1
return;
int t=tilet+,
s=size/2;
1/後盖左上角子棋盘
if (dr ‹tr+s && de‹tc+s)
ChessBoard (tr, tc, dr, dc, s);
else {
Board[tr+s-1][tc+s-1]=t;
ChessBoard(tr, tc, tr+s-1, tc+s-1, s);
if (dr < tr+s&& de ›= tc+s)
ChessBoard(tr, tc+s, dr, dc, s);
else {
Board[tr+s-11 tc+s] = t;
ChessBoard(tr, tc+s, tr+s-1, tc+s, s);
if (dr ›= tr+s && dc < tc+s)
ChessBoard (tr+s, tc, dr, dc, s);
else {
Board[tr+s][tc+s-1] = t;
ChessBoard(tr+s, tc, tr+s, tc+s-1, s);
if (dr ›= tr+s && dc ›= tc+s)
//L型骨牌号
//分割棋盘
//特殊方格在此栱盘中
//此栱盘中无特殊方格
//用七号山型骨牌覆盖右下角
//覆盖其余方格
//爱盖右上角子棋盘
//特殊方格在此棋盘中
//此棋盘中无特殊方格
//用七号L型骨牌覆盖左下角
//覆盖其余方格
//覆盖左下角子棋盘
//特殊方格在此棋盘中
//用七号山型骨牌覆盖右上角
//覆盖其余方格
//爱盖右下角子棋盘上述算法中用一个二维整型数组 Board 表示棋甜。BoarcroIrO1是棋盘的左上角方格。
是算法中的一个全局性型交量,用表示工 型骨牌的编号,其初始值为 0。算法的输入珍数是
切:棋盘左上角方格的行号;
dc:特殊方格所在的列号;
tc:棋盘左上角方格的列号;
size: size=2%,棋盘规格为 2*x2%,
dr:特殊方格所在的行号。
设TK是算法 ChessBoard 覆盖
一个2*x2*棋盘所需的时间,则从算法的分治策略可知,
『满足如下递归方程
(O(1)
k= 0
T(k) ={AT(k -1) + O()
解此递归方程可得

7(=0(45。由于覆盖一个242%棋盘所需的L 型骨牌个数为(4'-1/3
故算法 ChessBoard 是一个在渐近意义下最优的算法。

相关文章:

2.6 棋盘覆盖
在一个2*x2‘个方格组成的棋盘中,若怡有一个方格与其他方格不同,则称该方格为特殊方格,且称该棋盘为一特殊棋盘。显然,特殊方格在棋盘上出现的位置有 4种情形因而对任何k0,有4‘种特殊棋盘。图2-4 申的特殊棋益是12时 …...

JMU软件20 大数据技术复习(只写了对比18提纲的变动部分)
原博主 博客主页:https://xiaojujiang.blog.csdn.net/ 原博客链接:https://blog.csdn.net/qq_43058685/article/details/117883940 本复习提纲只适用于JMU软件工程大数据课程(ckm授课) 具体内容参考老师提纲的考纲,18和…...

MySQL底层存储B-Tree和B+Tree原理分析
1.B-Tree的原理分析 (1)什么是B-Tree B-树,全称是 Balanced Tree,是一种多路平衡查找树。 一个节点包括多个key (数量看业务),具有M阶的B树,每个节点最多有M-1个Key。 节点的key元素个数就是指这个节点能…...

基于Vue+Vue-cli+webpack搭建渐进式高可维护性前端实战项目
本文是专栏《手把手带你做一套毕业设计毕业设计》的实战第一篇,将从Vue脚手架安装开始,逐步带你搭建起一套管理系统所需的架构。当然,在默认安装完成之后,会对文件目录进行初步的细化拆分,以便后续功能迭代和维护所用。…...

第十三章:Java反射机制
第十三章:Java反射机制 13.1:Java反射机制概述 Java Reflection Reflection(反射)是被视为动态语言的关键,反射机制允许程序在执行期借助于Reflection API取得任何类的内部信息,并能直接操作任意对象的内部属性及方法。 加…...

iLok USB不识别怎么办?
我的iLok USB坏了吗? 我的iLok USB没有被系统或软件识别。 如果您的iLok USB未被识别,问题可能出在iLok USB、iLok软件或受保护的软件。 提示如果您使用USB集线器,请确保您使用正确的集线器电源适配器。排除硬件:将iLok USB直接插…...
【LeetCode与《代码随想录》】二叉树篇:做题笔记与总结-JavaScript版
文章目录代码随想录144. 二叉树的前序遍历94. 二叉树的中序遍历145. 二叉树的后序遍历102.二叉树的层序遍历226.翻转二叉树101. 对称二叉树104.二叉树的最大深度111.二叉树的最小深度222.完全二叉树的节点个数110.平衡二叉树257. 二叉树的所有路径404.左叶子之和513.找树左下角…...

机器人运动|浅谈Time Elastic Band算法
前言在自主移动机器人路径规划的学习与开发过程中,我接触到Time Elastic Band算法,并将该算法应用于实际机器人,用于机器人的局部路径规划。在此期间,我也阅读了部分论文、官方文档以及多位大佬的文章,在此对各位大佬的…...

【Linux】网络基础(1)
前言 相信没有网络就没有现在丰富的世界。本篇笔记记录我在Linux系统下学习网络基础部分知识,从关于网络的各种概念和关系开始讲起,逐步架构起对网络的认识,对网络编程相关的认知。 我的上一篇Linux文章呀~ 【Linux】网络套接字编程_柒海啦的…...

限流算法详解
限流是我们经常会碰到的东西,顾名思义就是限制流量。它能保证我们的系统不会被突然的流量打爆,保证系统的稳定运行。像我们生活中,地铁就会有很多护栏,弯弯绕绕的,这个就是一种限流。像我们抢茅台,肯定大部…...
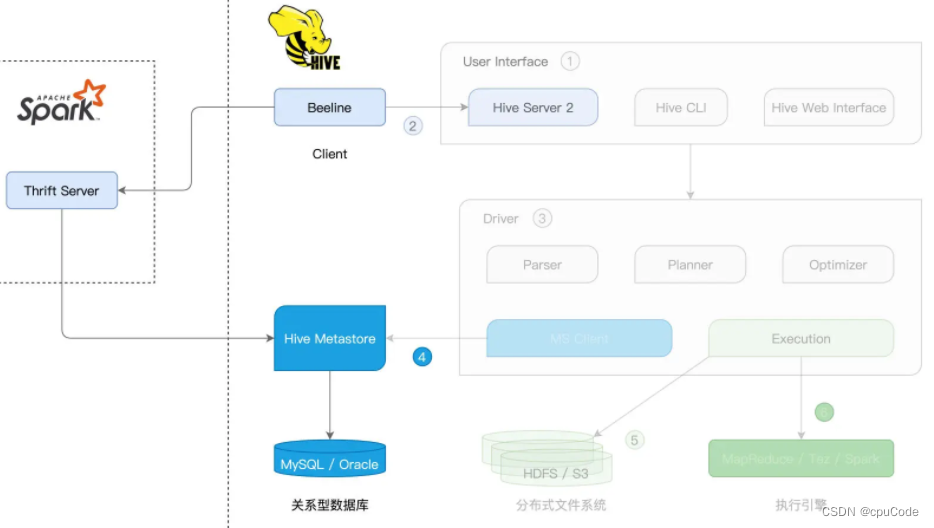
Spark/Hive
Spark/HiveHive 原理Spark with HiveSparkSession Hive Metastorespark-sql CLI Hive MetastoreBeeline Spark Thrift ServerHive on SparkHive 擅长元数据管理Spark 擅长高效的分布式计算 Spark Hive 集成 : Hive on Spark : Hive 用 Spark 作为底层的计算引擎时Spark w…...
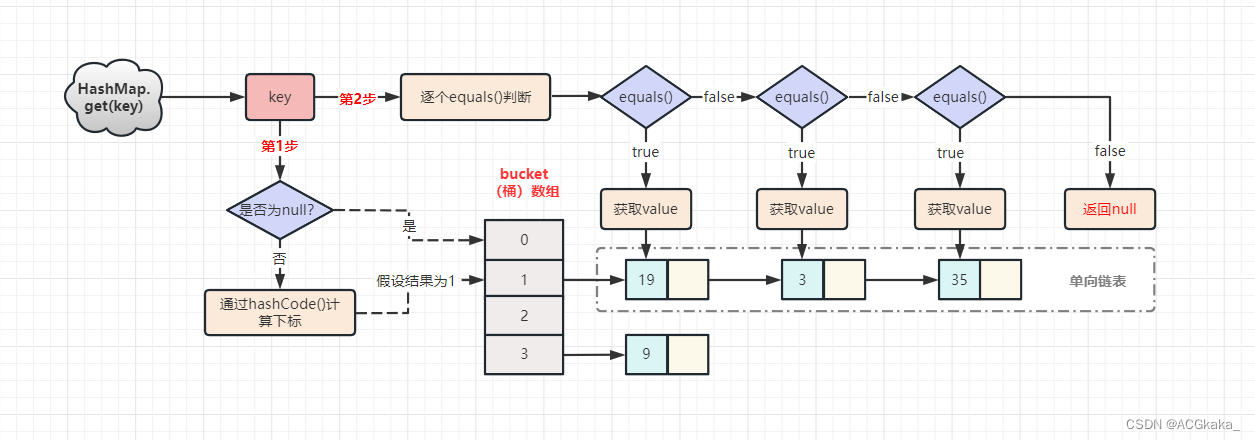
HashMap底层的实现原理(JDK8)
目录一、知识点回顾二、HashMap 的 put() 和 get() 的实现2.1 map.put(k, v) 实现原理2.2 map.get(k) 实现原理三、HashMap 的常见面试题3.1 为何随机增删、查询效率都很高?3.2 为什么放在 HashMap 集合 key 部分的元素需要重写 equals 方法?3.3 HashMap 的 key 为…...
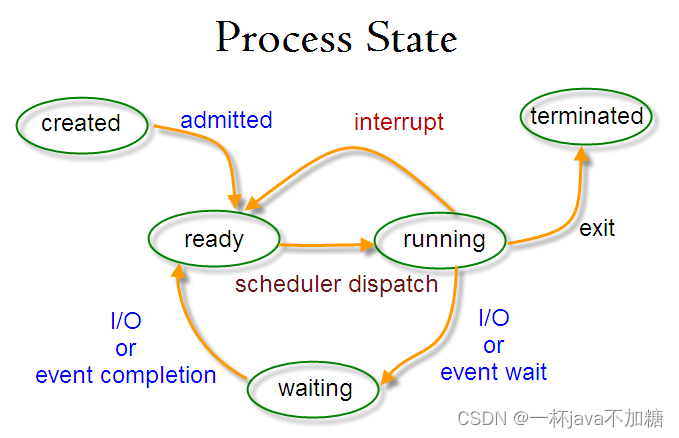
操作系统-整理
进程 介绍 进程是系统进行资源分配和调度的一个独立单位。每个进程都有自己的独立内存空间,不同进程通过进程间通信来通信。由于进程占据独立的内存,所以上下文进程间的切换开销(栈、寄存器、虚拟内存、文件句柄等)比较大&#…...
系统换行符的思考
各系统换行符 换行符,也即是回车换行,因为表示为Carriage-Return和Line-Feed。 回车用Return-Carrige表示,简写为CR,字符表示为\r。 换行用Line-Feed表示,简写为LF,字符表示为\n。 由于历史原因…...
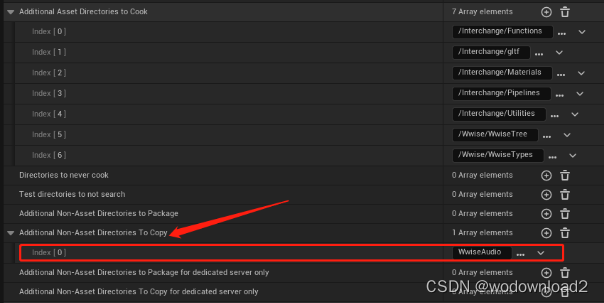
Wwise集成到unreal
1、Wwise集成到Unreal 1.1 安装必要的软件 安装unreal 5.1;安装Audiokinetic Launcher;集成版本是Wwise 2021.1.12.7973。Audiokinetic Launcher下载地址: https://www.audiokinetic.com/zh/thank-you/launcher/windows/?refdownload&pl…...

前端秘籍之=>八股文经卷=>(原生Js篇)【持续更新中...】
大家好,最近想了想,打算总结归纳一版前端八股文经卷,给大家提供学习参考,如果帮助到大家,请大家,一键三连支持一下,你们的支持会激励我更加努力的更新更多有用的知识,博主先在这里谢…...
【Python安装配置教程】
Python由荷兰数学和计算机科学研究学会的吉多范罗苏姆于1990年代初设计,作为一门叫做ABC语言的替代品。Python提供了高效的高级数据结构,还能简单有效地面向对象编程。Python语法和动态类型,以及解释型语言的本质,使它成为多数平台…...

Spring-Retry失败重试
文章目录 重试的场景引入依赖启动类serviceController@Retryable参数@Recover注意事项重试的场景 1、网络波动需要,导致请求失败,需要重发。 2、发送消息失败,需要重发,重发失败要记录日志 … 引入依赖 <!-- spring-retry--> <dependency><groupId>or…...
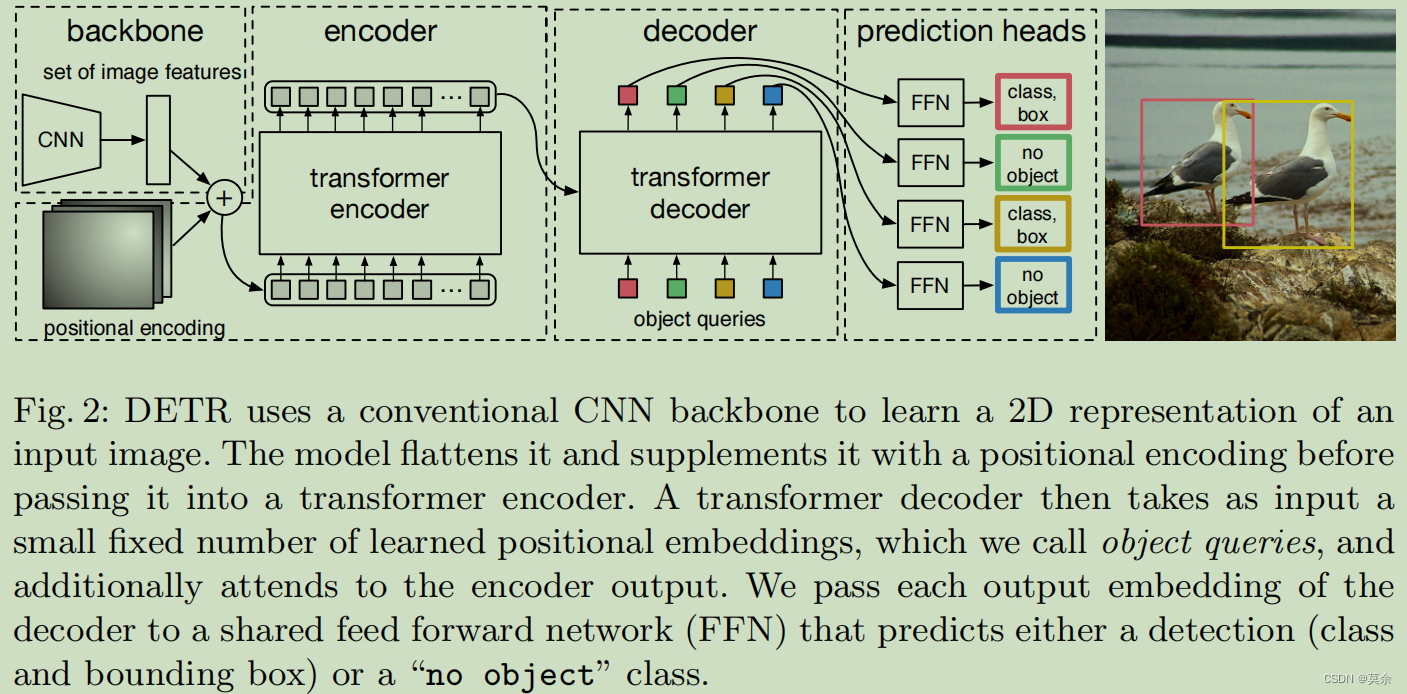
【目标检测 DETR】通俗理解 End-to-End Object Detection with Transformers,值得一品。
文章目录DETR1. 亮点工作1.1 E to E1.2 self-attention1.3 引入位置嵌入向量1.4 消除了候选框生成阶段2. Set Prediction2.1 N个对象2.2 Hungarian algorithm3. 实例剖析4. 代码4.1 配置文件4.1.1 数据集的类别数4.1.2 训练集和验证集的路径4.1.3 图片的大小4.1.4 训练时的批量…...

项目ER图和资料
常用的数据类型 模型类 一对多 from app import db import datetimeclass BaseModel(db.Model):__abstract__ Truecreate_time db.Column(db.DateTime,defaultdatetime.datetime.now())update_time db.Column(db.DateTime,defaultdatetime.datetime.now())class Role(db.M…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...
