MySQL底层存储B-Tree和B+Tree原理分析
1.B-Tree的原理分析
(1)什么是B-Tree
-
B-树,全称是 Balanced Tree,是一种多路平衡查找树。
-
一个节点包括多个key (数量看业务),具有M阶的B树,每个节点最多有M-1个Key。
-
节点的key元素个数就是指这个节点能够存储几个数据。
-
每个节点最多有m个子节点,最少有M/2个子节点,其中M>2。
-
数据集合分布在整个树里面,叶子节点和非叶子节点都存储数据;类似在整个树里面做一次二分查找。
-
B 树相对于平衡二叉树,每个节点存储了更多的键值(key)和数据(data)。
-
实际业务中B树的阶数一般大于100,存储大量数据,B树高度也会很低,查询效率会更高。
-
备注
-
每个节点拥有最多的子节点,子节点的个数一般称为阶。
-
阶:m阶是代表每个节点最多有m个分支(子树)。
-
树的度:这棵树里面节点最大的度。
-
节点的度:当前节点有几个子节点。
-

(2)B树插入原理
- 每个节点的数据都是顺序存储,具有M阶的B树,树的阶数表示每个结点最多可以有多少个子结点

(3)B树的应用场景
- 在数据库中,B树用来维护索引,用来提高查询效率,一个节点可以存储整个页(即磁盘块)
- 在文件系统中,B树用来存储文件的目录信息,提高文件的访问效率
- 在操作系统中,B树可以用来存储内存管理信息,提高内存的分配效率
(4)思考:3层的B树,阶数为1024,最多容纳多少个元素?
-
B树的阶数表示每个结点最多可以有多少个子结点,因此B树的阶数为1024,表示每个结点最多可以有1024个子结点
-
由于B树的3层,因此根结点可以有1024个子结点,每个子结点又可以有1024个子结点
-
因此一个3层的B树,阶数为1024,B树的每一层的节点数都是阶数的幂次方
-
计算总容量 把每一层的节点数相加 即10241+10242+1024^3 大约是 11亿个节点,假如每个节点放一个元素就是11亿个
-
所以在10亿个数据中找目标值,常规小于3次磁盘IO即可找到目标值,比平衡二叉树的30次提升了不少
-
平衡二叉树的高度就等于每次查询数据时磁盘 IO 操作的次数。
-
10亿的数据量,log2(N)约等于30次磁盘IO,
- log2(N) 相当于2的多少次方(立方)等于N,例:log2 (8)= 3
- 2的30次方=1073741824,所以就是30次磁盘IO
-
2.B+Tree的原理分析
(1)什么是B+Tree
- 是B树的一种变形形式,B+树上的叶子结点存储关键字以及相应记录的地址,同等存储空间下比B-Tree存储更多key
- 非叶子节点不对关键字记录的指针进行保存,只进行数据索引 , 树的层级会更少 , 所有叶子节点都在同一层,
- 叶子节点的关键字从小到大有序排列,叶子节点之间用指针连接, 构成有序链表(稠密索引)
- B+树上每个非叶子节点之间是一个双向链表进行链接,而叶子节点中的数据都是使用单向链表链接
- 查找特点
- 当索引部分某个结点的关键字与所查的关键字相等时,并不停止查找
- 继续沿着关键字的指针向下,每次查询必须到叶子节点才能真正获取到相关数据
- B+Tree叶子节点相连接,对树的遍历就是只需要 一次线性遍历叶子节点
- 由于叶子节点的数据是顺序排列,方便区间查找
- 在B+树完成范围查找,排序查找,分组查找,去重查找 比B树效率也比较高

(2)B+Tree插入流程解析

-
总结
-
B树和B+树的最大区别在于非叶子节点是否存储数据
-
B+树非叶子节点只是当索引使用,同等空间下B+树存储更多key
-
B树,非叶子节点和叶子节点都会存储数据,找到对应节点就有对应的数据
-
B+树, 只有叶子节点才会存储数据,存储的数据都是在一行上,找到非叶子节点的key,还需要继续找到叶子节点才可以获取数据
-
B树的节点包括了key-value,所以找到对应的key即可找到对应的value,不用在继续寻找
-
两种树各有优缺点和应用场景
-
3.B+Tree树应用之Mysql索引底层原理剖析
-
背景
-
Mysql数据库是大家用最多的,查询是最高频使用的操作
-
在多数数据库的设计里面,会用B-Tree或B+Tree做索引提高查询效率
-
-
基于一张数据库的表数据进行查询(类似mysql的user表)
-
构建索引:id用做key,然后data是数据的存储地址
| 内存地址 | id | phone | name | Age |
|---|---|---|---|---|
| 0xFS | 843 | 13820835467 | 张三 | 43 |
| 0xER | 984 | 15738235423 | 李四 | 20 |
| 0x32 | 4212 | 12152354223 | 王五 | 18 |
| 0x93 | 1000 | 12152356324 | 赵六 | 30 |
| 0xAP | 2341 | 18735622097 | 李祥 | 19 |
| 0xSQ | … 1千万条数据 | … | … | … |
-
精确查找 id=2341的数据
select * from user where id = 2341-
未使用索引
- 自上而下查找数据,一行行遍历,5次才找到数据
-
使用索引
- id建立主键索引(B+Tree结构),对应的数据存储数据的地址,2次找到数据,且数据量越多效果越明显
- 根节点是常驻内存的,不需要进行IO操作
-
-
范围查找 id>1000 和 id < 4212 的用户
-
未使用索引
- 自上而下查找数据,一行行遍历
-
使用索引
- id建立主键索引(B+Tree结构),由于本身是有序链表,所以顺序查找即可
-
-
Mysql的InnoDB中的索引结构与MyISAM的索引结构的区别
-
InnoDB引擎,表数据文件按B+Tree组织的,叶节点data域保存完整行数据, 树上的key就是主键, 以主键构建的B+树索引
-
这种索引叫做聚集索引(聚簇索引 clustered index)
-
聚簇索引一般为主键索引,而主键一个表中只能有一个,所以聚集索引一个表只能有一个
-
聚簇索引叶子节点存储的是行数据,而非聚簇索引叶子节点存储的是聚簇索引(通常是主键 ID)
-
-
MyISAM引擎:索引文件和数据文件是分开的,索引结构的叶子节点放的是指向数据的主键(或者是地址)构建的B+树索引
- 这种索引叫做非聚集索引、二级索引、辅助索引(非聚簇索引 nonclustered index)
- 非聚集索引一个表可以存在多个
- 叶子节点中保存的不是实际数据,而是主键,获得主键值后去聚簇索引中获得数据行
-
注意
-
非聚簇索引的叶子节点上存储的并不是真正的行数据,而是主键 ID或记录的地址
-
当使用非聚簇索引进行查询时,会得到一个主键 ID,再使用主键 ID 去聚簇索引上找真正的行数据,把这个过程称之为回表查询
-
所以聚簇索引查询效率更高,而非聚簇索引需要进行回表查询,性能不如聚簇索引
-
非聚簇索引的叶子节点上存储的并不是真正的行数据,而是主键 ID或记录的地址
-
当使用非聚簇索引进行查询时,会得到一个主键 ID,再使用主键 ID 去聚簇索引上找真正的行数据,把这个过程称之为回表查询
-
所以聚簇索引查询效率更高,而非聚簇索引需要进行回表查询,性能不如聚簇索引
-

相关文章:

MySQL底层存储B-Tree和B+Tree原理分析
1.B-Tree的原理分析 (1)什么是B-Tree B-树,全称是 Balanced Tree,是一种多路平衡查找树。 一个节点包括多个key (数量看业务),具有M阶的B树,每个节点最多有M-1个Key。 节点的key元素个数就是指这个节点能…...

基于Vue+Vue-cli+webpack搭建渐进式高可维护性前端实战项目
本文是专栏《手把手带你做一套毕业设计毕业设计》的实战第一篇,将从Vue脚手架安装开始,逐步带你搭建起一套管理系统所需的架构。当然,在默认安装完成之后,会对文件目录进行初步的细化拆分,以便后续功能迭代和维护所用。…...

第十三章:Java反射机制
第十三章:Java反射机制 13.1:Java反射机制概述 Java Reflection Reflection(反射)是被视为动态语言的关键,反射机制允许程序在执行期借助于Reflection API取得任何类的内部信息,并能直接操作任意对象的内部属性及方法。 加…...

iLok USB不识别怎么办?
我的iLok USB坏了吗? 我的iLok USB没有被系统或软件识别。 如果您的iLok USB未被识别,问题可能出在iLok USB、iLok软件或受保护的软件。 提示如果您使用USB集线器,请确保您使用正确的集线器电源适配器。排除硬件:将iLok USB直接插…...
【LeetCode与《代码随想录》】二叉树篇:做题笔记与总结-JavaScript版
文章目录代码随想录144. 二叉树的前序遍历94. 二叉树的中序遍历145. 二叉树的后序遍历102.二叉树的层序遍历226.翻转二叉树101. 对称二叉树104.二叉树的最大深度111.二叉树的最小深度222.完全二叉树的节点个数110.平衡二叉树257. 二叉树的所有路径404.左叶子之和513.找树左下角…...

机器人运动|浅谈Time Elastic Band算法
前言在自主移动机器人路径规划的学习与开发过程中,我接触到Time Elastic Band算法,并将该算法应用于实际机器人,用于机器人的局部路径规划。在此期间,我也阅读了部分论文、官方文档以及多位大佬的文章,在此对各位大佬的…...

【Linux】网络基础(1)
前言 相信没有网络就没有现在丰富的世界。本篇笔记记录我在Linux系统下学习网络基础部分知识,从关于网络的各种概念和关系开始讲起,逐步架构起对网络的认识,对网络编程相关的认知。 我的上一篇Linux文章呀~ 【Linux】网络套接字编程_柒海啦的…...

限流算法详解
限流是我们经常会碰到的东西,顾名思义就是限制流量。它能保证我们的系统不会被突然的流量打爆,保证系统的稳定运行。像我们生活中,地铁就会有很多护栏,弯弯绕绕的,这个就是一种限流。像我们抢茅台,肯定大部…...
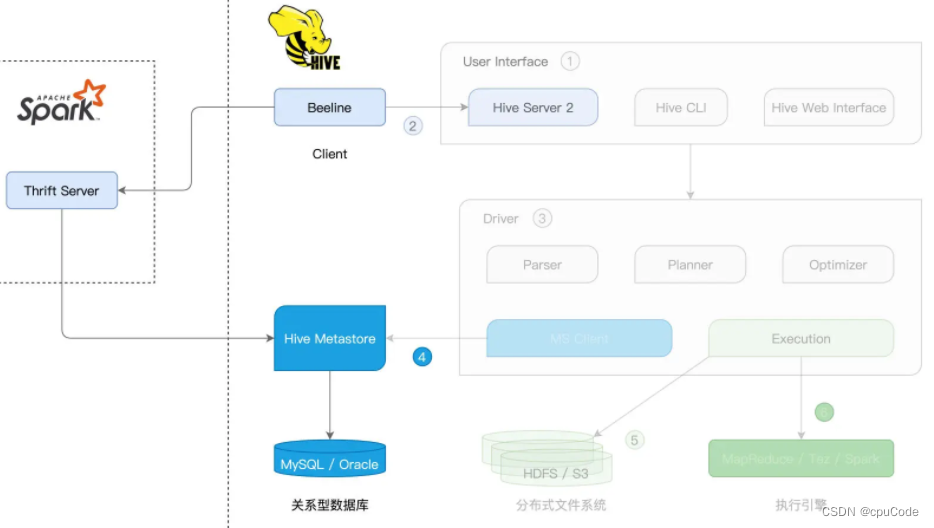
Spark/Hive
Spark/HiveHive 原理Spark with HiveSparkSession Hive Metastorespark-sql CLI Hive MetastoreBeeline Spark Thrift ServerHive on SparkHive 擅长元数据管理Spark 擅长高效的分布式计算 Spark Hive 集成 : Hive on Spark : Hive 用 Spark 作为底层的计算引擎时Spark w…...
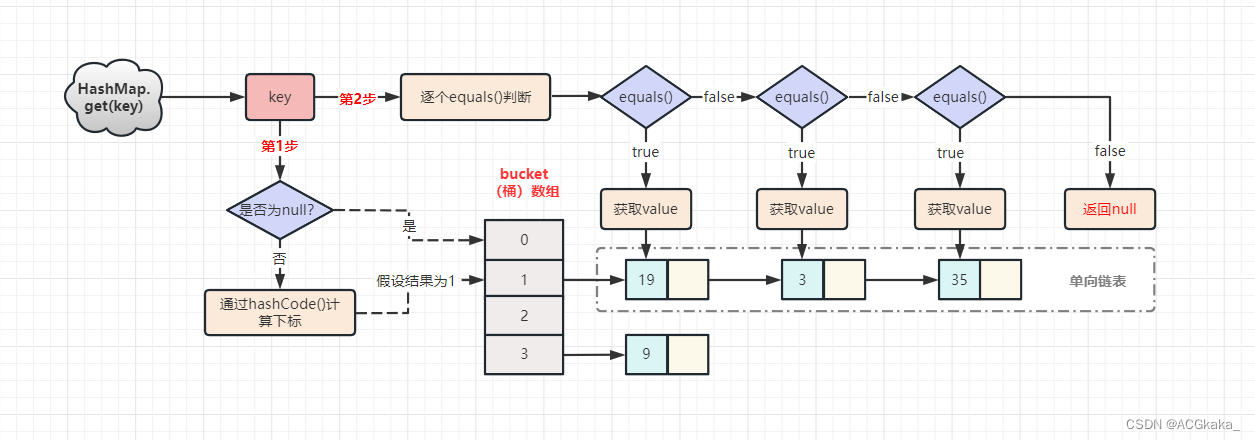
HashMap底层的实现原理(JDK8)
目录一、知识点回顾二、HashMap 的 put() 和 get() 的实现2.1 map.put(k, v) 实现原理2.2 map.get(k) 实现原理三、HashMap 的常见面试题3.1 为何随机增删、查询效率都很高?3.2 为什么放在 HashMap 集合 key 部分的元素需要重写 equals 方法?3.3 HashMap 的 key 为…...
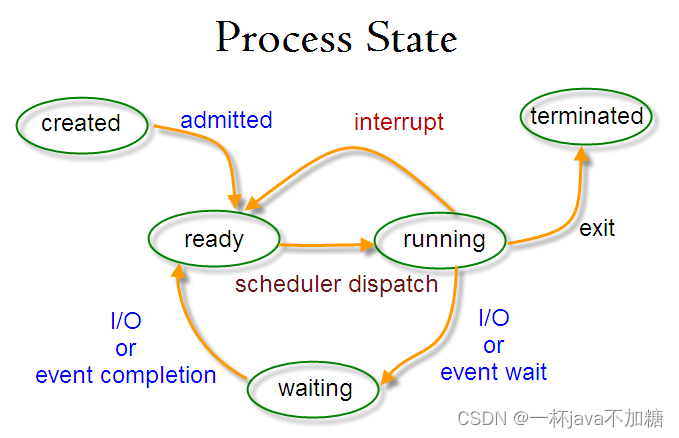
操作系统-整理
进程 介绍 进程是系统进行资源分配和调度的一个独立单位。每个进程都有自己的独立内存空间,不同进程通过进程间通信来通信。由于进程占据独立的内存,所以上下文进程间的切换开销(栈、寄存器、虚拟内存、文件句柄等)比较大&#…...
系统换行符的思考
各系统换行符 换行符,也即是回车换行,因为表示为Carriage-Return和Line-Feed。 回车用Return-Carrige表示,简写为CR,字符表示为\r。 换行用Line-Feed表示,简写为LF,字符表示为\n。 由于历史原因…...
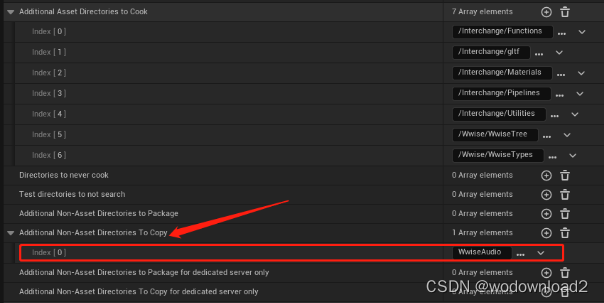
Wwise集成到unreal
1、Wwise集成到Unreal 1.1 安装必要的软件 安装unreal 5.1;安装Audiokinetic Launcher;集成版本是Wwise 2021.1.12.7973。Audiokinetic Launcher下载地址: https://www.audiokinetic.com/zh/thank-you/launcher/windows/?refdownload&pl…...

前端秘籍之=>八股文经卷=>(原生Js篇)【持续更新中...】
大家好,最近想了想,打算总结归纳一版前端八股文经卷,给大家提供学习参考,如果帮助到大家,请大家,一键三连支持一下,你们的支持会激励我更加努力的更新更多有用的知识,博主先在这里谢…...
【Python安装配置教程】
Python由荷兰数学和计算机科学研究学会的吉多范罗苏姆于1990年代初设计,作为一门叫做ABC语言的替代品。Python提供了高效的高级数据结构,还能简单有效地面向对象编程。Python语法和动态类型,以及解释型语言的本质,使它成为多数平台…...

Spring-Retry失败重试
文章目录 重试的场景引入依赖启动类serviceController@Retryable参数@Recover注意事项重试的场景 1、网络波动需要,导致请求失败,需要重发。 2、发送消息失败,需要重发,重发失败要记录日志 … 引入依赖 <!-- spring-retry--> <dependency><groupId>or…...
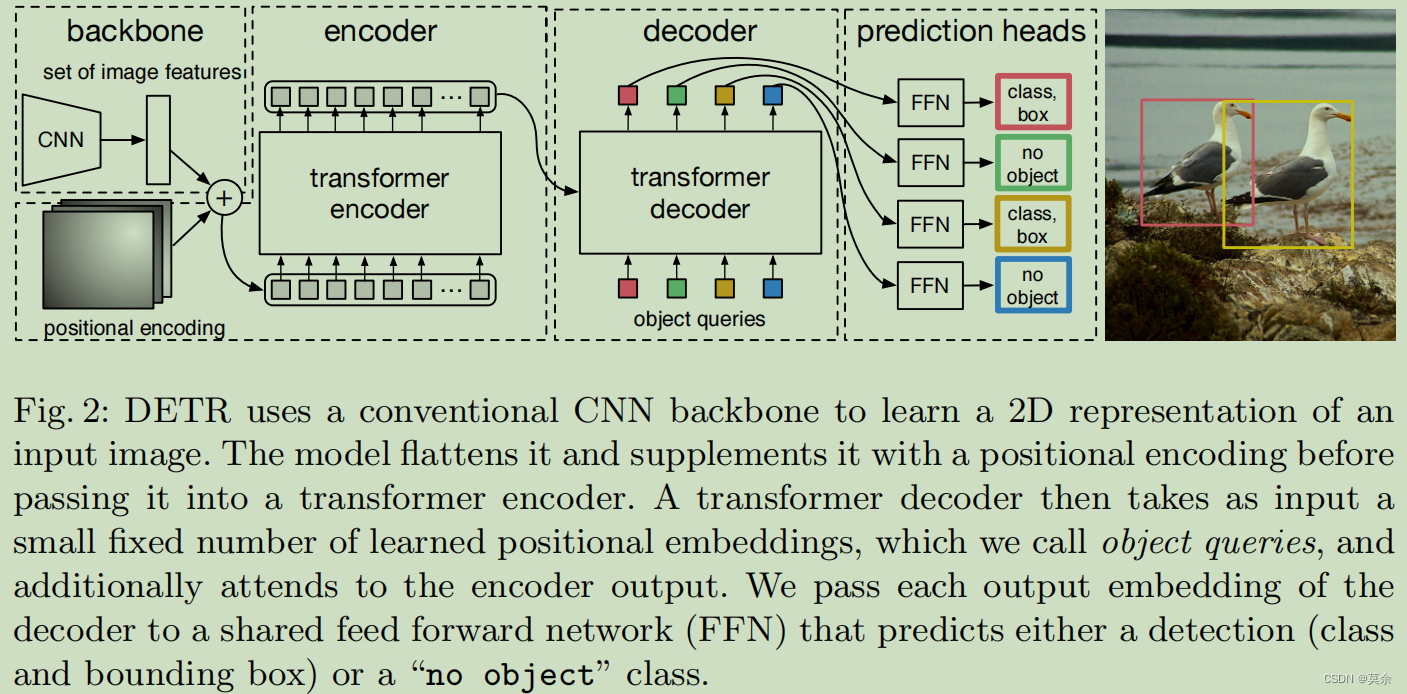
【目标检测 DETR】通俗理解 End-to-End Object Detection with Transformers,值得一品。
文章目录DETR1. 亮点工作1.1 E to E1.2 self-attention1.3 引入位置嵌入向量1.4 消除了候选框生成阶段2. Set Prediction2.1 N个对象2.2 Hungarian algorithm3. 实例剖析4. 代码4.1 配置文件4.1.1 数据集的类别数4.1.2 训练集和验证集的路径4.1.3 图片的大小4.1.4 训练时的批量…...

项目ER图和资料
常用的数据类型 模型类 一对多 from app import db import datetimeclass BaseModel(db.Model):__abstract__ Truecreate_time db.Column(db.DateTime,defaultdatetime.datetime.now())update_time db.Column(db.DateTime,defaultdatetime.datetime.now())class Role(db.M…...
)
剑指 Offer 20. 表示数值的字符串(java+python)
请实现一个函数用来判断字符串是否表示数值(包括整数和小数)。 数值(按顺序)可以分成以下几个部分: 若干空格 一个 小数 或者 整数 (可选)一个 ‘e’ 或 ‘E’ ,后面跟着一个 整数…...

程序员的逆向思维
前要: 为什么你读不懂面试官提问的真实意图,导致很难把问题回答到面试官心坎上? 为什么在面试结束时,你只知道问薪资待遇,不知道如何高质量反问? 作为一名程序员,思维和技能是我们职场生涯中最重要的两个方面。有时候…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...
