动态规划专练( 231.打家劫舍Ⅱ)
231.打家劫舍Ⅱ
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
示例 1:
输入:nums = [2,3,2]
输出:3
解释:你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。
示例 2:
输入:nums = [1,2,3,1]
输出:4
解释:你可以先偷窃 1 号房屋(金额 = 1),然后偷窃 3 号房屋(金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。
示例 3:
输入:nums = [1,2,3]
输出:3
提示:
1 <= nums.length <= 1000 <= nums[i] <= 1000
题解:
本题在198.打家劫舍的基础上进行了变化,将首尾两个元素连成了环,成环之后思考的难度提高了很多,因为如过要使用动态规划的话,不知道从哪个位置开始。
因此第一步是将本题进行转换。首尾成环相较于没有成环,其实是多了三种情况。
- 情况一:我不考虑首尾元素,只考虑中间部分
- 情况二:我不考虑尾元素,只考虑首元素和中间部分
- 情况三:我不考虑首元素,只考虑中间部分和尾元素
在这三种情况中,其实情况一的值一定是小于等于情况二和情况三的。因为情况二和三考虑的范围包括住了情况一,在一个更大的范围内求解最大值,一定是大于等于的关系。
因此可以将情况二和情况三分别拆分成两个数组,送入到198.打家劫舍的算法中,再取最大值即可.
package com.offer;/*** @author bwzfy* @create 2024/4/16**/
public class _213打家劫舍Ⅱ {public static void main(String[] args) {System.out.println(rob(new int[]{2, 3, 2}));}public static int rob(int[] nums) {if (nums.length == 1) {return nums[0];}// 三种选择// 两头都不考虑(这种情况其实包含在了下面两种情况中,因此只要考虑下面两种情况下的最大值就可以了)// 只考虑头// 只考虑尾return Math.max(rob(nums, 0, nums.length - 2), rob(nums, 1, nums.length - 1));}private static int rob(int[] nums, int left, int right) {if (right == left) {// 如果只有一个元素直接返回return nums[left];}int[] dp = new int[right - left + 1];// 只考虑一户人家的时候,最多能拿多少钱dp[0] = nums[left];// 只考虑两户人家的时候,最多能拿多少钱dp[1] = Math.max(nums[left], nums[left + 1]);for (int i = 2; i <= right - left; i++) {dp[i] = Math.max(dp[i - 1], nums[left + i] + dp[i - 2]);}return dp[right - left];}
}相关文章:
)
动态规划专练( 231.打家劫舍Ⅱ)
231.打家劫舍Ⅱ 你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间…...

K-means和逻辑回归
逻辑回归 一个事件的几率是该事件发生的概率/该事件不发生的概率:P/(1-P) 对数几率是:log(P/(1-P)) **考虑对输入x分类的模型:**log(P/(1-P))wx 则 Pexp(wx)/(exp(w*x)…...

3.2 iHRM人力资源 - 组织架构 - 编辑及删除
iHRM人力资源 - 组织架构 文章目录 iHRM人力资源 - 组织架构一、编辑功能1.1 表单弹层并数据回显1.2 编辑校验1.3 编辑 二、删除功能 一、编辑功能 编辑功能和新增功能用的组件其实是一个,结构几乎是一样的,其实是复用了组件,我们也省去了很…...
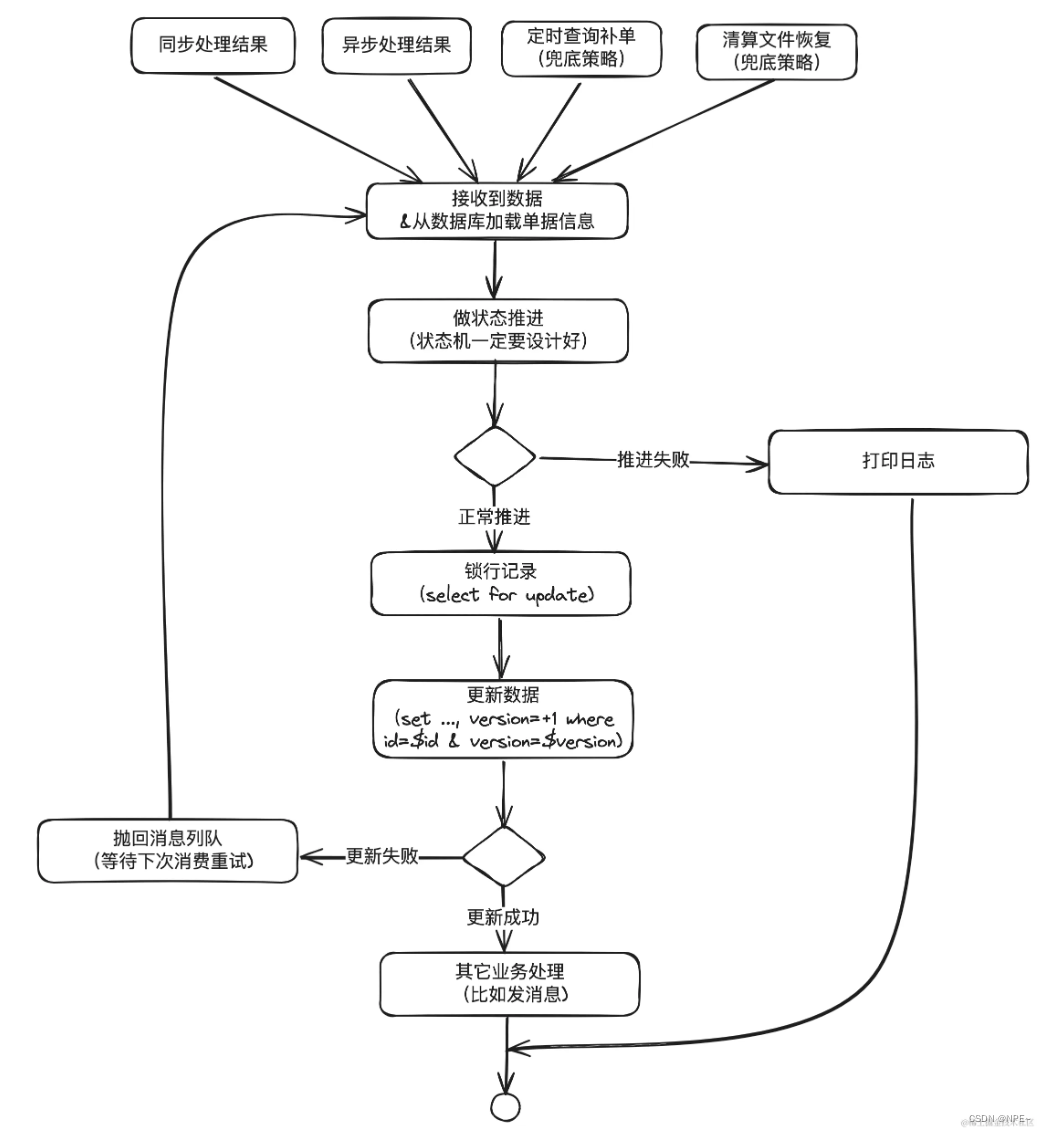
支付系统核心逻辑 — — 状态机(JavaGolang版本)
支付系统核心逻辑 — — 状态机 代码地址:https://github.com/ziyifast/ziyifast-code_instruction/tree/main/state_machine_demo 1 概念:FSM(有限状态机),模式之间转换 状态机,也叫有限状态机(…...

rest_framework_mongoengine实现后端的增删改查
rest_framework_mongoengine实现后端增删改查 一、增删改查 1. 继承ModelViewSet实现增删改查 父urls.py path("api/testapp/", include("apps.testapp.urls")), # 测试子urls.py # -*- coding: utf-8 -*- from django.urls import path from res…...

【精读文献】Scientific data|2017-2021年中国10米玉米农田变化制图
论文名称:Mapping annual 10-m maize cropland changes in China during 2017–2021 第一作者及通讯作者:Xingang Li, Ying Qu 第一作者单位及通讯作者单位:北京师范大学地理学部 文章发表期刊:《Scientific data》(…...

高光谱图像修复笔记
目录 RetinexFormer 也有MST-plus-plus代码,分辨率可以调 MST-plus-plus github地址: WACV2023 DSTrans RetinexFormer GitHub - caiyuanhao1998/Retinexformer: "Retinexformer: One-stage Retinex-based Transformer for Low-light Image E…...
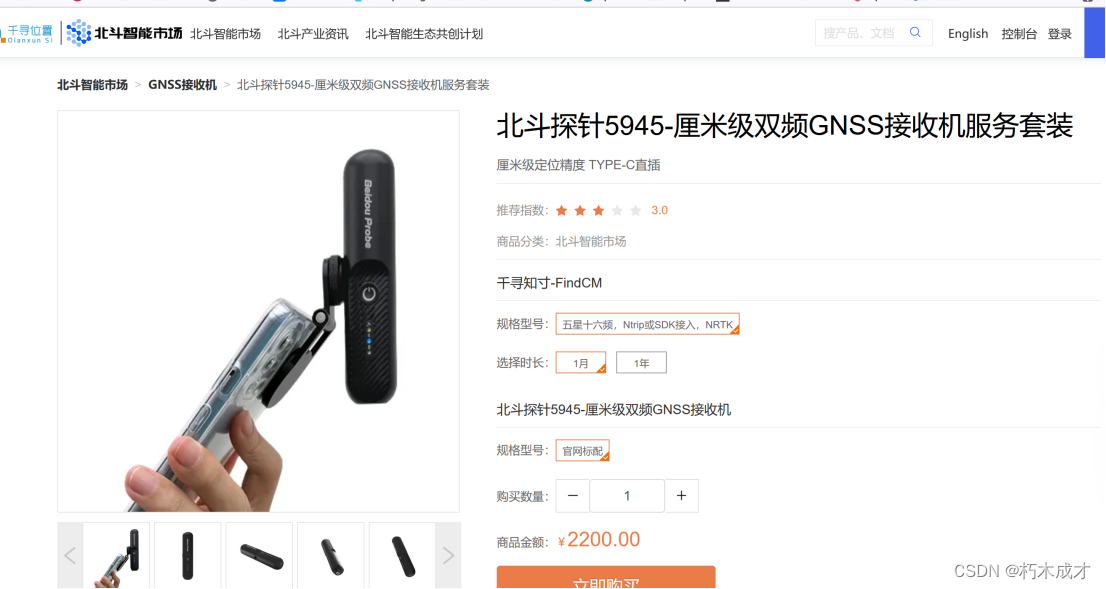
GPS定位原理及应用分析
一.定位原理 1.卫星定位(GPS,北斗导航) ①.硬件构成(24颗卫星,可构建一套导航系统) 为何是24颗卫星? 可以做到全球覆盖,同一地点地球上空可观测到4颗卫星。 …...

Java面试篇9——并发编程
并发编程知识梳理 提示,此仅为面试,若想对线程有跟完整了解,请点击这里 提示:直接翻到最后面看面试真题,上面的为详解 面试考点 文档说明 在文档中对所有的面试题都进行了难易程度和出现频率的等级说明 星数越多代表…...
[RK3399 Linux] 使用busybox 1.36.1制作rootfs
一、 编译、安装、配置 busybox 1.1 下载源码 根文件系统是根据busybox来制作的。 下载地址:https://busybox.net/downloads/。 这里就以1.36.1版本为例进行编译安装介绍: 注意:编译linux内核与文件系统中的所有程序要使用相同的交叉编译器。 下载完成后解压: mkdir …...

JavaScript入门--循环
JavaScript入门--循环 一、for循环二、for in语句三、break语句四、continue语句五、while循环六、do-while语句一、for循环 先来看一个循环案例: for (i = 0; i < 5; i++) {...
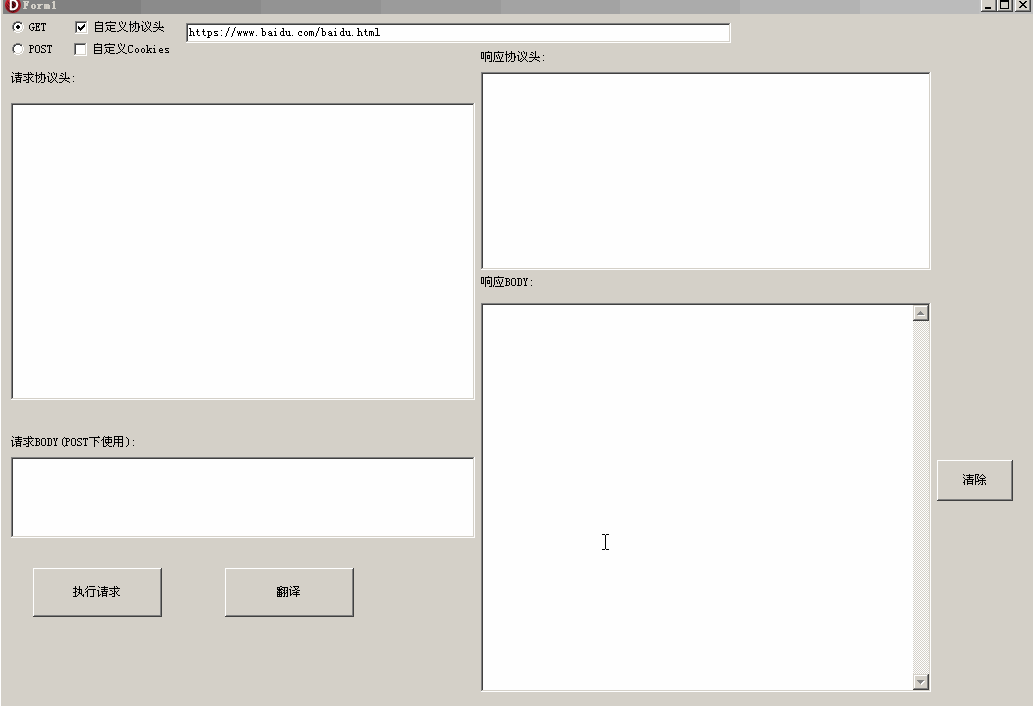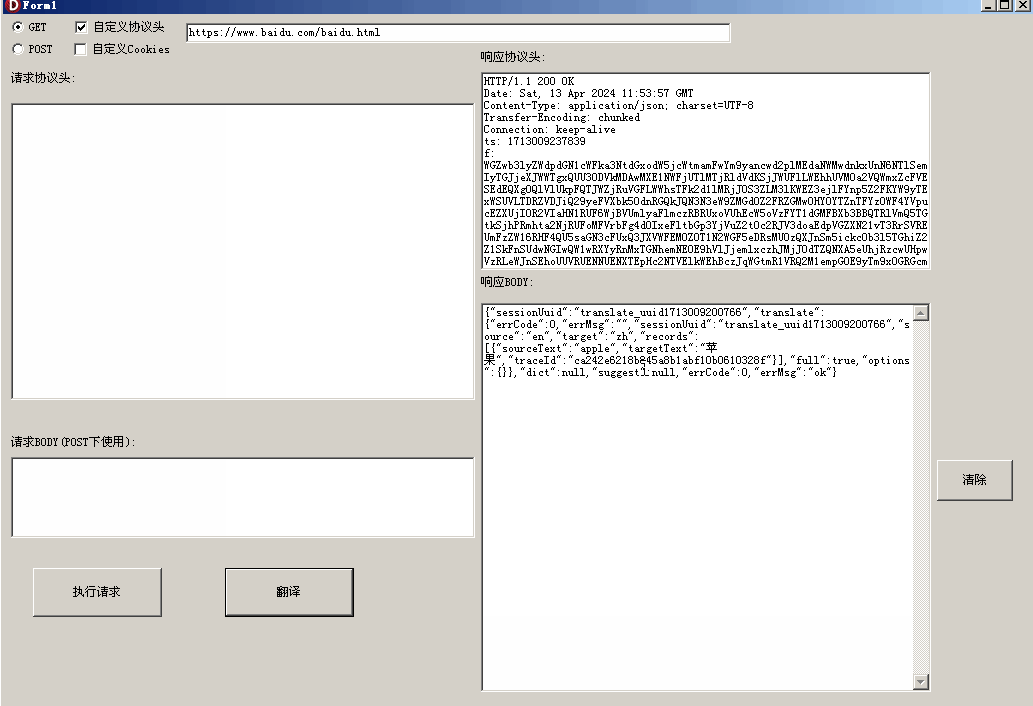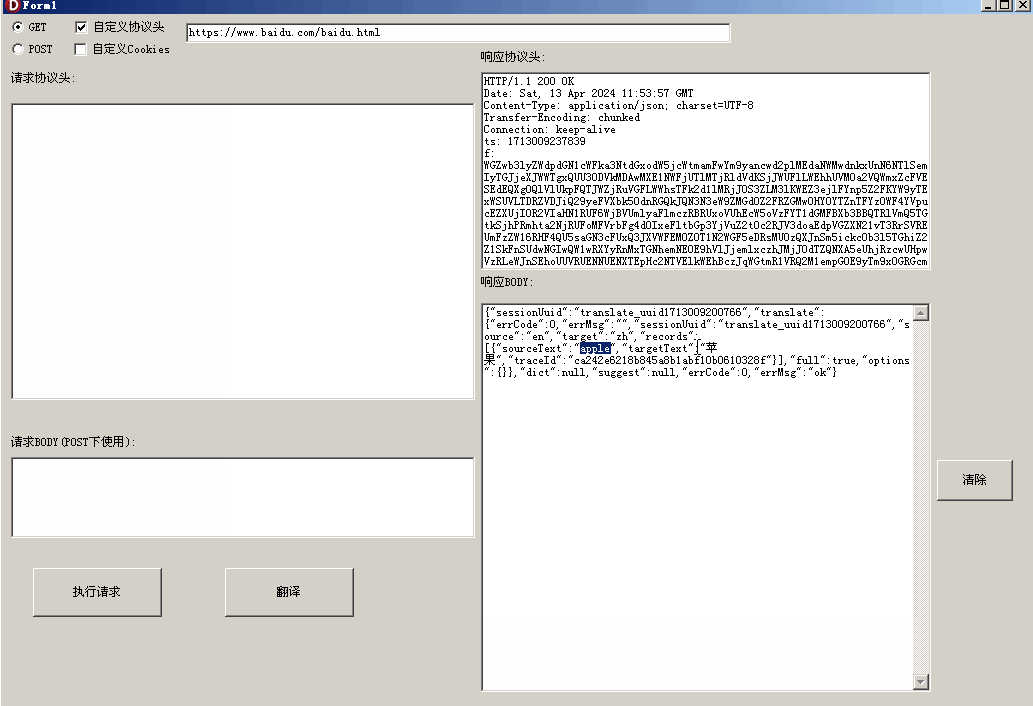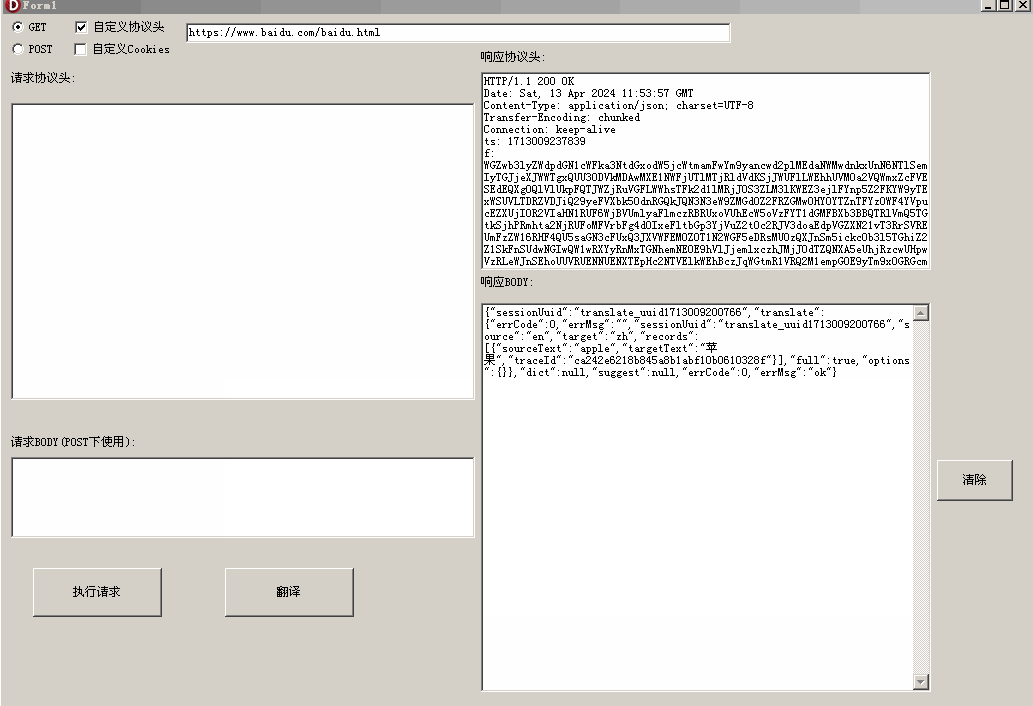
【Delphi 爬虫库 1】GET和POST方法
文章目录 1.最简单的Get方法实现2.可自定义请求头、自定义Cookie的Get方法实现3.提取响应协议头4.Post方法实现单词翻译 爬虫的基本原理是根据需求获取信息并返回。就像当我们感到饥饿时,可以选择自己烹饪食物、外出就餐,或者订外卖一样。在编程中&#…...

[leetcode] 快乐数 E
:::details 编写一个算法来判断一个数 n 是不是快乐数。 「快乐数」 定义为: 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。 然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。 如果这个过程 结果为 1…...
Lobe UI - 基于 AntDesign 开发的 AIGC Web 应用的开源 UI 组件库
今天推荐一个可以快速开发 ChatGPT UI 界面的组件库,质量很高,拿来就能用。 Lobe UI 是由 lobehub 团队开发的一套 web UI 组件库,和我之前推荐的很多通用型的 UI 组件库不同,Lobe UI 是专门为目前火热的 AIGC 应用开发而打造&am…...

Java常用类 -- Random类
该类实例用于生成伪随机数的流 伪随机数:通过算法算出来的数,是假的随机数 (一)具体使用 public static void main(String[] args) { Random r new Random(); System.out.println("随机出int类型的数据" r.nextIn…...

Docker安装Kong网关
文章目录 一、kong是什么?二、搭建步骤1.搭建PostgreSQL2.搭建Kong网关2.1、制作镜像2.2、数据库初始化2.3、启动Kong网关一、kong是什么? Github地址:https://github.com/Kong/kong Kong是一个可扩展、开源的云原生API网关,可以在分布式环境中管理、监控和安全地发布API…...

spispispi
SPI C.. & C.. logic是SPI的控制逻辑,芯片内部进行地址锁存、数据读写等操作,都是由控制逻辑自动完成。控制逻辑的左边是SPI的通信引脚,这些引脚和主控芯片相连,主控芯片通过SPI协议,把指令和数据发送给控制逻辑&a…...

MySQL——创建和插入
一、插入数据 INSERT 使用建议; 在任何情况下建议列出列名,在 VALUES 中插入值时,注意值和列的意义对应关系 values 指定的值顺序非常重要,决定了值是否被保存到正确的列中 在指定了列名的情况下,你可以仅对需要插入的列给到…...

【BUG】element-ui表格中使用video标签,数据翻页,video中的视频仍然显示第一页的视频,没有重新加载
BUG描述 遇到一个问题,使用element-ui构建的管理端后台,表格里面每一行都有一个video标签,里面有视频,当我翻页了以后,视频不会重新加载,仍然显示的是第一页的视频,代码如下: <e…...
【JavaSE】你真的了解内部类吗?
前言 本篇会详细讲解内部类的四种形式,让你掌握内部类~ 欢迎关注个人主页:逸狼 创造不易,可以点点赞吗~ 如有错误,欢迎指出~ 目录 前言 内部类介绍 实例内部类 定义 调用 静态内部类 定义 调用 匿名内部类 定义和调用1 调用方法2 …...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...
