R 格式(蓝桥杯)
文章目录
- R 格式
- 【问题描述】
- 解题思路
- 高精度乘法+高精度加法
R 格式
【问题描述】
小蓝最近在研究一种浮点数的表示方法:R 格式。对于一个大于 0 的浮点数 d,可以用 R 格式的整数来表示。给定一个转换参数 n,将浮点数转换为 R格式整数的做法是:
- 将浮点数乘以 2n;
- 四舍五入到最接近的整数。
【输入格式】
一行输入一个整数 n 和一个浮点数 d,分别表示转换参数,和待转换的浮点数。
【输出格式】
输出一行表示答案:d 用 R 格式表示出来的值。
【样例输入】
2 3.14
【样例输出】
13
【样例说明】
3.14 × 22 = 12.56,四舍五入后为 13。
【评测用例规模与约定】
对于 50% 的评测用例:1 ≤ n ≤ 10,1 ≤ 将 d 视为字符串时的长度 ≤ 15。
对于 100% 的评测用例:1 ≤ n ≤ 1000,1 ≤ 将 d 视为字符串时的长度≤ 1024;保证 d 是小数,即包含小数点。
解题思路
题意分析:
- 将浮点数乘以 2n;
- 四舍五入到最接近的整数。
根据题意将d * 2n分解为d * 2 * 2 * 2 * 2 * 2……(这里2的n次方不能使用pow函数,当n过大,会得不到答案),因为d长度小于等于1024,所以可以使用高精度乘法的算法来实现
然后该如何去乘?这里我先给出结论:
一个小数乘以一个大于0的整数时,小数点位数本身不会改变,但小数点后面的数字可能会发生变化。乘法操作并不改变数字中小数点的位置,它只是会影响小数点前后的数字值。 所以,我们先将小数看作一个整数相乘即可,例如:1.05 * 2=105 * 2=210=2.10
四舍五入:最后看小数点第一位是否大于等于5,如果大于等于5,前一位需要+1,需要注意的是这里可能存在连续进位,例如9999.5应该四舍五入为10000,所以这里因该使用高精度加法的算法
高精度乘法+高精度加法
#include<bits/stdc++.h>
using namespace std;// 乘法函数,用于将向量 a 中的每个元素乘以整数 n,并返回结果向量
vector<int> mul(vector<int> a,int n)
{vector<int> c; // 结果向量int t=0; // 用于累计进位for(int i=0;i<a.size()||t;i++){if(i<a.size()) t+=a[i]*n; // 计算当前位与 n 的乘积加上之前的进位c.push_back(t%10); // 将乘积的个位数加入结果向量t/=10; // 更新进位}return c; // 返回结果向量
} // 加法函数,用于将向量 b 的每个元素与整数 n 相加,并返回结果向量
vector<int> sum(vector<int> b,int n)
{vector<int> c; // 结果向量int t=0; // 用于累计进位for(int i=0;i<b.size();i++){t+=b[i]; // 加上当前位的值if(n) t+=n%10; // 如果 n 不为零,则加上 n 的当前位c.push_back(t%10); // 将和的个位数加入结果向量t/=10; // 更新进位n/=10; // 更新 n,移动到下一位}if(t) c.push_back(t); // 如果最后还有进位,加到结果向量的末尾return c; // 返回结果向量
}int main()
{int n; // 转换参数 nstring s; // 待转换的浮点数 d 作为字符串cin>>n>>s; // 从输入读取 n 和 sstring t; // 用于存储去掉小数点后的数字字符串int k=0; // 小数点后数字的个数// 移除小数点,并计算 kfor(int i=0;i<s.size();i++){if(s[i]!='.')t+=s[i];elsek=i; }k=t.size()-k; // 计算小数点后的位数vector<int> a; // 存储数字的向量,每个元素是一位数字// 将字符串 t 的数字转换为向量 afor(int i=t.size()-1;i>=0;i--)a.push_back(t[i]-'0'); // 将 a 乘以 2^nfor(int i=1;i<=n;i++)a=mul(a,2);reverse(a.begin(),a.end()); // 反转结果向量,以便从最高位开始处理int p=a[a.size()-k]; // 获取可能需要四舍五入的位if(p>=5) // 如果需要四舍五入{vector<int> b;// 构造需要增加 1 的向量 bfor(int i=a.size()-1-k;i>=0;i--){b.push_back(a[i]);}b=sum(b,1); // 对 b 加 1for(int i=b.size()-1;i>=0;i--)cout<<b[i]; // 输出结果}else // 如果不需要四舍五入{for(int i=0;i<a.size()-k;i++)cout<<a[i]; // 直接输出结果}return 0;
}
代码大致流程:
- 读取输入的转换参数
n和浮点数s。 - 去除
s中的小数点,并计算出小数点后的位数k。 - 将处理过的数字转换为一个由单个数字组成的向量
a,并对其进行n次乘以 2 的操作。 - 判断是否需要进行四舍五入,根据判断结果输出最终的整数值。
此代码通过数位分离和模拟手算乘法、加法的方式,精确地处理了大数问题,确保了在面对极大的 n 时仍能正确计算并避免浮点数精度问题。
相关文章:
)
R 格式(蓝桥杯)
文章目录 R 格式【问题描述】解题思路高精度乘法高精度加法 R 格式 【问题描述】 小蓝最近在研究一种浮点数的表示方法:R 格式。对于一个大于 0 的浮点数 d,可以用 R 格式的整数来表示。给定一个转换参数 n,将浮点数转换为 R格式整数的做法…...

Intellij idea的快速配置详细使用
IntelliJ IDEA是一款强大的集成开发环境(IDE),支持多种编程语言,包括Java、Kotlin、Scala等。以下是关于IntelliJ IDEA的快速配置和使用的详细步骤: 一、安装 前往IntelliJ IDEA的官方网站或可靠的软件下载平台&…...
JavaEE:JVM
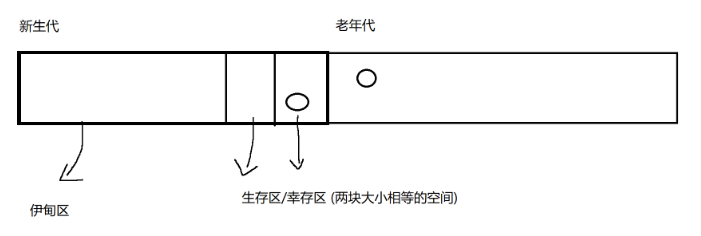
基本介绍 JVM:Java虚拟机,用于解释执行Java字节码 jdk:Java开发工具包 jre:Java运行时环境 C语言将写入的程序直接编译成二进制的机器语言,而java不想重新编译,希望能直接执行。Java先通过javac把.java…...
Linux基础|线程池Part.1|线程池的定义和运行逻辑
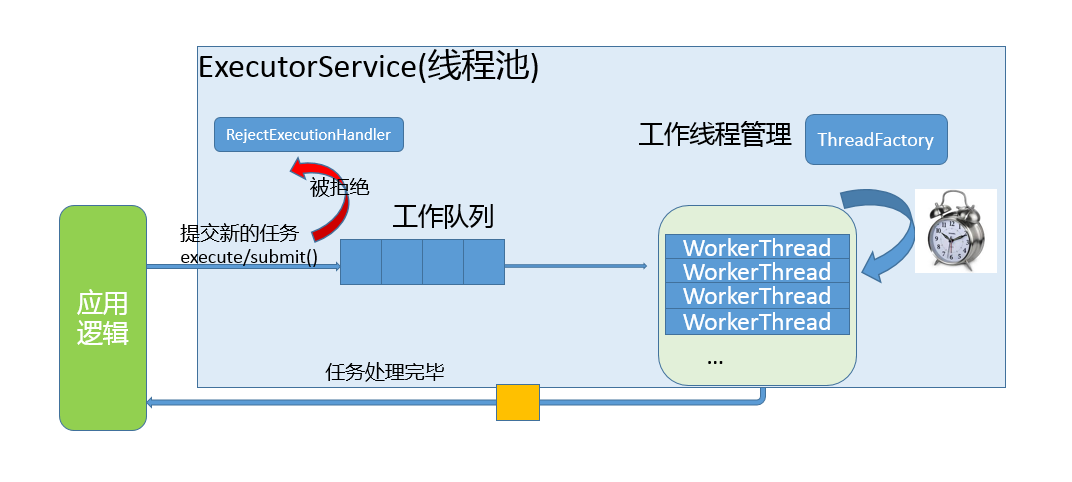
线程池的定义和运行逻辑 多线程的问题: 如果并发的线程数量很多,并且每个线程都是执行一个时间很短的任务就结束了,这样频繁创建线程就会大大降低系统的效率,因为频繁创建线程和销毁线程需要时间。 那么一个很自然的想法就出现了…...

蓝队面试经验总结
Sql注入 1、sql注入漏洞原理 开发者没有在网页传参点做好过滤,导致恶意 sql 语句拼接到数据库进行执行 2、sql注入分类 联合注入 、布尔盲注 、时间盲注 、堆叠注入 、宽字节注入 、报错注入 3、堆叠注入原理 在 mysql 中,分号 代表一个查询语句的…...

MySQL命令分类与大纲
一、数据库管理 创建与删除数据库 CREATE DATABASE:创建新数据库DROP DATABASE:删除已存在的数据库ALTER DATABASE:修改数据库属性 切换与查看数据库 USE:选择当前工作数据库SHOW DATABASES:列出所有可用数据库 二、…...

windows编译xlnt,获取Excel表里的数据
用git拉取项目 这个文件是空的 要用git拉下来,使用终端编译xlnt库 点击解决方案 运行生成 然后新建项目,配置好库, #include <iostream> #include <xlnt/xlnt.hpp>int main() {// 打开 Excel 文件xlnt::workbook workbook;workb…...

c#字段和属性的区别
在C#中,字段(fields)和属性(properties)都是类的成员,它们提供了类存储数据的方式,但它们在用途和功能上有着明显的区别。 字段 字段通常用来存储类或结构的状态信息。字段是类的数据成员&…...

微软正式发布Copilot for Security
微软公司近日宣布,其备受期待的安全自动化解决方案——Copilot for Security现已全面上市,面向全球用户开放。这一创新工具的推出标志着微软在提升企业安全防护能力方面迈出了重要一步,同时也为安全专业人士提供了强大的支持。 Copilot for …...

AI大模型日报#0416:李飞飞《2024年人工智能指数报告》、Sora加入Adobe、李彦宏聊百度大模型之路
导读: 欢迎阅读《AI大模型日报》,内容基于Python爬虫和LLM自动生成。目前采用“文心一言”生成了每条资讯的摘要。标题: 刚刚,李飞飞团队发布《2024年人工智能指数报告》:10大趋势,揭示AI大模型的“喜”与“忧” 摘…...
OpenCV轻松入门(八)——图片卷积
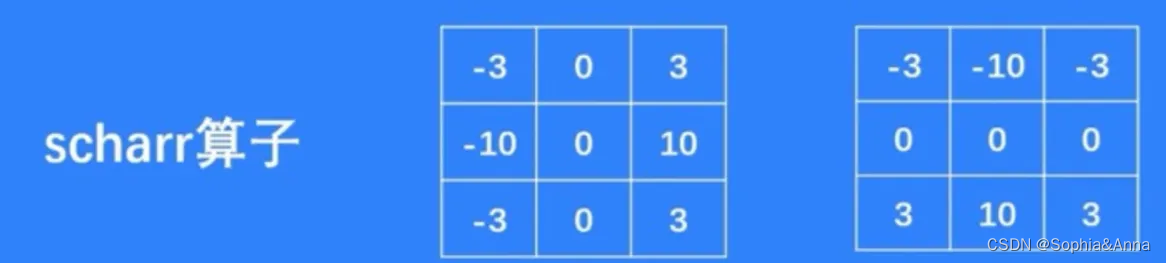
对图像和滤波矩阵进行逐个元素相乘再求和的操作就相当于将一个二维的函数移动到另一个二维函数的所有位置,这个操作就叫卷积。 卷积需要4个嵌套循环,所以它并不快,除非我们使用很小的卷积核。这里一般使用3x3或者5x5 图像滤波 图像滤波是尽…...

鸿蒙HarmonyOS开发规范-完善中
代码规范 所有文件,包括自动生成的编译文件package.json都要格式化(IDE快捷键CtrlAltL);函数命名,C大驼峰,TS、JS小驼峰,函数命名注意动宾结构;静态常量需使用全大写,文…...
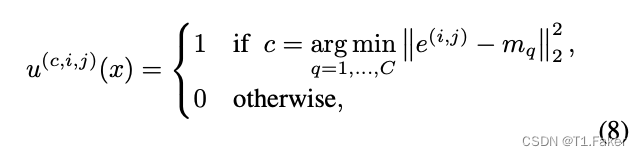
神经网络压缩图像
简介 典型的压缩管道由四个组件组成: 编码:输入图像 x x x通过编码器函数 ε \varepsilon ε,将其转换为潜在表示 z z z。 量化:截断 z z z以丢弃一些不重要的信息 熵编码:使用某种形式的熵编码(例如&…...
)
Catagory(rt)
继承(IMP融合):支持super命令码;继承推荐重写 分类(IMP替换):不支持super命令码;分类推荐组合 //替换(原来没了/破坏掉原来IMP/分类(替换特性)) 情况1: 自封装(组件化)开源库>分类推荐组合 情况2:逆向分析> 有意替换>分类IMP替换 #import "CatagoryViewContro…...
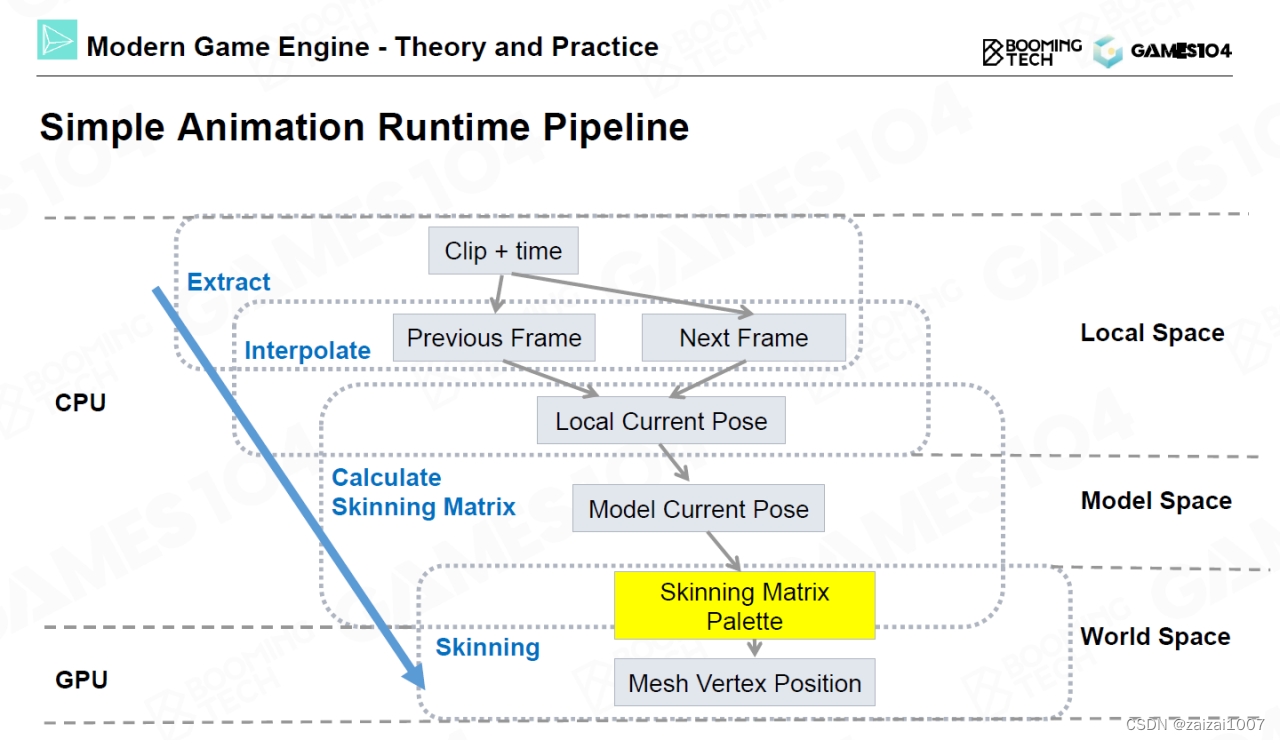
Games104 现代游戏引擎3
Sprite Animation 序列帧动画 自由度(degrees of freedom,DoF)对于刚体而言描述它的运动需要3个位移3个旋转,一共6个自由度 顶点动画(per-vertex animation)利用网格的顶点来控制运动。此时网格上的每个顶…...

【云计算】混合云分类
《混合云》系列,共包含以下 3 篇文章: 【云计算】混合云概述【云计算】混合云分类【云计算】混合云组成、应用场景、风险挑战 😊 如果您觉得这篇文章有用 ✔️ 的话,请给博主一个一键三连 🚀🚀Ὠ…...
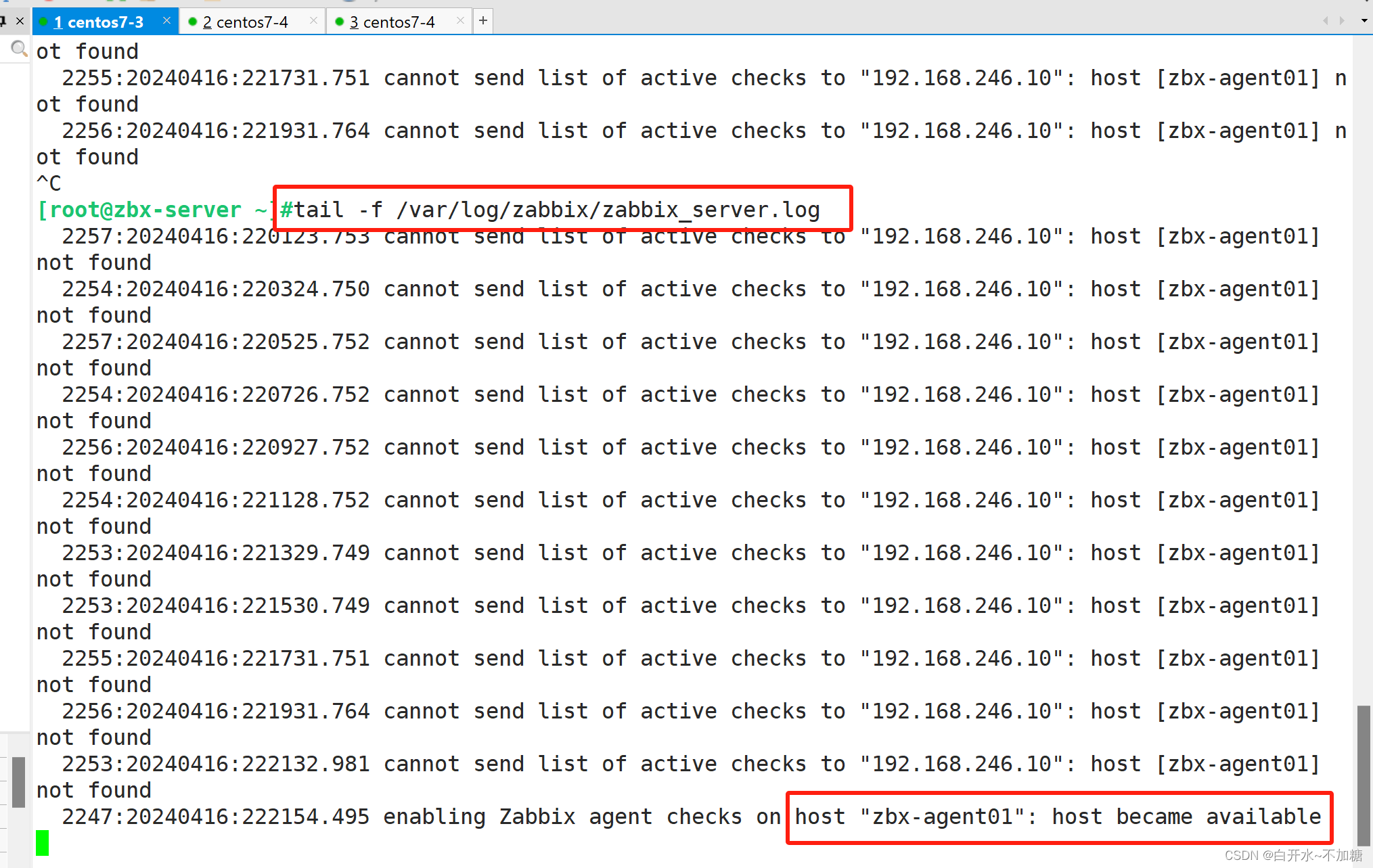
探索分布式系统监控zabbix------------自动发现与自动注册
目录 一、部署 zabbix 服务端 二、部署 zabbix 客户端 2.1环境准备 2.2服务端和客户端都配置时间同步 (ntp) 2.2.1服务端zbx-server 2.2.2服务端zabbix-agent01客户端 2.3客户端配置时区,与服务器保持一致 2.4设置 zabbix 的下载源&…...
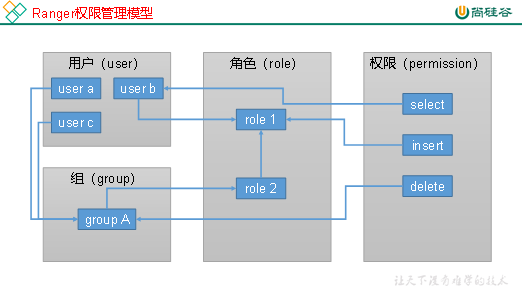
权限管理Ranger详解
文章目录 一、Ranger概述与安装1、Ranger概述1.1 Ranger介绍1.2 Ranger的目标1.3 Ranger支持的框架1.4 Ranger的架构1.5 Ranger的工作原理 2、Ranger安装2.1 创建系统用户和Kerberos主体2.2 数据库环境准备2.3 安装RangerAdmin2.4 启动RangerAdmin 二、Ranger简单使用1、安装 R…...
WPF Extended.Wpf.Toolkit 加载界面
1、NuGet 中安装 Extended.Wpf.Toolkit 。 2、在MainWindow.xaml中添加xmlns:tk"http://schemas.xceed.com/wpf/xaml/toolkit" 。 MainWindow.xaml 代码如下。 <Window x:Class"WPF_Extended_Wpf_Toolkit_Loading.MainWindow" xmlns"ht…...
【切换网络连接后】VMware虚拟机网络配置【局域网通信】
初次安装Linux虚拟机以及切换网络都需要配置虚拟机网络, 从而使得win主机内通过远程连接工具能够连接该虚拟机, 而不是在虚拟机内操作。 本片文章你将了解到网络切换后如何配置虚拟机网络的一些基础操作,以及局域网通信的一些基础知识。 …...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...
