C#面:泛型的主要约束和次要约束是什么
在 C# 中,泛型的约束是用来限制泛型类型参数的行为和能力的。
主要约束和次要约束是两种不同的约束方式。
主要约束(Primary Constraint):
主要约束指定了泛型类型参数必须满足的最基本的条件,它可以是一个类、一个接口或者一个特定的值类型。
主要约束使用 where T : 约束类型语法来定义,其中 T 是泛型类型参数,约束类型可以是类名、接口名或者值类型。
下面的代码定义了一个泛型方法,其中泛型类型参数 T 必须是实现了 IComparable 接口的类:
public void Compare<T>(T a, T b) where T : IComparable
{// 在这里可以使用IComparable接口的方法进行比较操作
}次要约束(Secondary Constraint):
次要约束是对泛型类型参数的额外限制,它可以是一个类、一个接口或者一个新的无参构造函数。
次要约束使用 where T : 约束类型语法来定义,其中T是泛型类型参数,约束类型可以是类名、口名或者无参构造函数。
下面的代码定义了一个泛型方法,其中泛型类型参数 T 必须是一个具有无参构造函数的类:
public T CreateInstance<T>() where T : new()
{return new T();
}官方文档:
where(泛型类型约束)- C# 参考 - C# | Microsoft Learn
相关文章:

C#面:泛型的主要约束和次要约束是什么
在 C# 中,泛型的约束是用来限制泛型类型参数的行为和能力的。 主要约束和次要约束是两种不同的约束方式。 主要约束(Primary Constraint): 主要约束指定了泛型类型参数必须满足的最基本的条件,它可以是一个类、一个接…...

Java使用documents4j将word和excel转pdf
pom.xml添加documents4j依赖 <!-- documents4j --> <dependency><groupId>com.documents4j</groupId><artifactId>documents4j-local</artifactId><version>1.0.3</version> </dependency> <!-- documents4j 转 wor…...

使用策略模式实现 Spring 分布式和单机限流
我们可以使用策略模式来统一单机限流和分布式限流的实现,提高代码的可扩展性和可维护性。 思路是定义一个 RateLimitStrategy 接口,并分别实现单机限流策略 LocalRateLimitStrategy 和分布式限流策略 DistributedRateLimitStrategy。在 AOP 切面中,根据配置决定使用哪种限流策…...

@CrossOrigin注解解决跨域问题
文章目录 一、什么是跨域二、CrossOrigin注解是干什么用的三、用法 一、什么是跨域 跨域,指的是浏览器不能执行其他网站的脚本。它是由浏览器的同源策略造成的,是浏览器对JavaScript施加的安全限制。 所谓同源是指,域名,协议&…...

【力扣】45. 跳跃游戏 II
Problem: 45. 跳跃游戏 II 文章目录 问题思路复杂度Code 问题 思路 核心思路,例如nums[i]5,那么最远能跳五步; //那么在这接下来1-5范围内,哪个能让我跳的最远,这个最远指的是 -------------------------------------…...

【Python基础】19.eval函数的使用
eval函数 eval()将字符串转变为有效的表达式来求值并返回对应的结果 基础数据计算 In [1]: eval("1 1") Out[1]: 2字符串重复 In [2]: eval (" * * 10") Out[2]: **********字符串转为列表 In [3]: type(eval("[1,2,3,4,5]")) Out[3]: lis…...

对装饰器模式的理解
目录 一、场景二、面对场景中的新需求,我们怎么办?1、暴力法:直接修改原有的代码。2、子类继承法:既然要增强行为,那我搞一个子类,覆写不就完事了?3、装饰器模式 三、对装饰器模式的思考1、从代…...

在替换微软AD的CA证书服务AD CS前,要先做哪些准备工作?
AD CS是什么 关于这个问题,有几个概念需要先弄明白:PKI、CA、数字证书。 PKI(Public Key Infrastructure,公钥基础设施)是提供公钥加密和数字签名服务的系统或平台,实现基于公钥密码体制的密钥和证书的产生…...

Java中的System
文章目录 概要小结 概要 在Java中,System类提供了一些静态方法来实现与系统相关的操作。以下是System类中常用的方法及其含义: System.currentTimeMillis():返回当前时间(以毫秒为单位)自1970年1月1日00:00:00 GMT以来…...

Mybites一对多collection
Goods实体属性: private List<GoodsImg> goodsImgList; private String id; private String name; GoodsImg实体属性: private String id; private String fid; private String imgpath; …...
基于springboot实现图书进销存管理系统项目【项目源码+论文说明】计算机毕业设计
基于springboot实现图书进销存管理系统演示 摘要 随着信息技术在管理上越来越深入而广泛的应用,管理信息系统的实施在技术上已逐步成熟。本文介绍了图书进销存管理系统的开发全过程。通过分析图书进销存管理系统管理的不足,创建了一个计算机管理图书进销…...

敏捷开发:想要快速交付就必须舍弃产品质量?
随着敏捷的推广与应用,如今已经成为了最有效的团队级别的方法论,越来越多的软件和 IT 团队正在采用敏捷,但是你在敏捷吗? 自从那一群充满影响力的软件从业者聚集在一起并发布了《敏捷宣言》以来,已经过去了 23 年。敏…...

SNMP-详解指南
目录 SNMP介绍 SNMP的工作机制轮询 SNMP的MIB(管理信息库) SNMP是基于UDP协议 SNMP介绍 SNMP(Simple Network Management Protocol,简单网络管理协议)是一种广泛应用于互联网上的网络管理协议。它提供了一种标准化…...
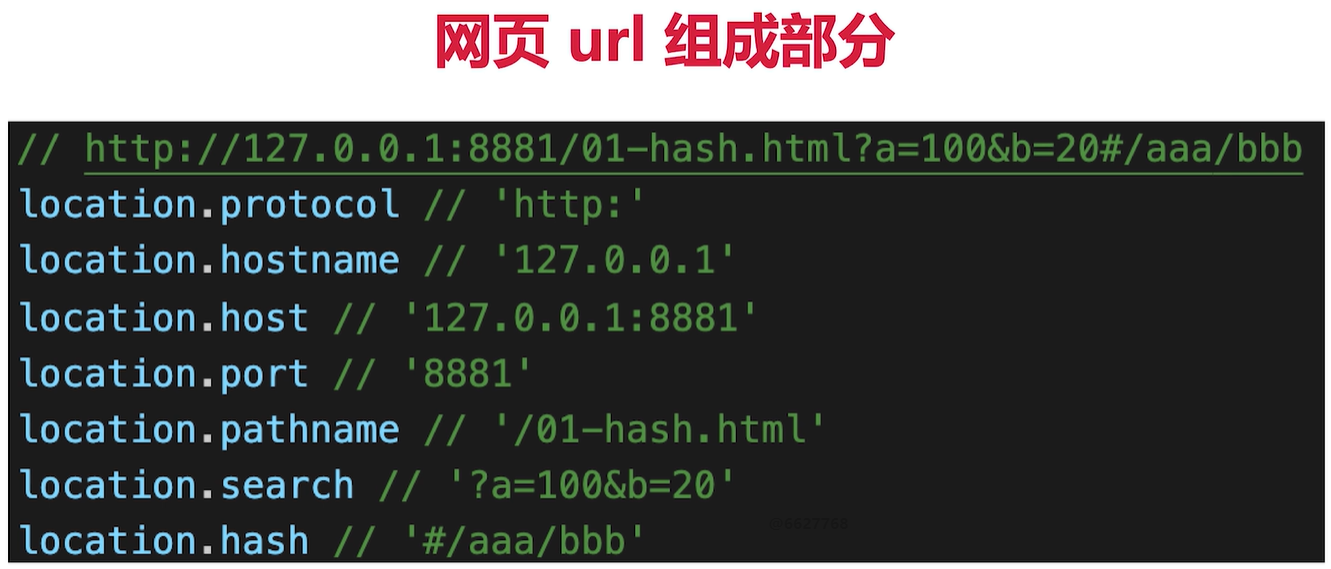
vue-router 原理【详解】hash模式 vs H5 history 模式
hash 模式 【推荐】 路由效果 在不刷新页面的前提下,根据 URL 中的 hash 值,渲染对应的页面 http://test.com/#/login 登录页http://test.com/#/index 首页 核心API – window.onhashchange 监听 hash 的变化,触发视图更新 window.onhas…...

WebGl/Three 粒子系统 人物破碎及还原运动
粒子 首先,加载模型,这是万千粒子的前身,模型对象由很多面构成,这些面又是由各个点构成的,所以可以将模型的几何体对象geometry赋给粒子对象,粒子物体用Points方式渲染 bloader.load("obj/female02/Fe…...

华为OD-C卷-分披萨[100分]
题目描述 "吃货"和"馋嘴"两人到披萨店点了一份铁盘(圆形)披萨,并嘱咐店员将披萨按放射状切成大小相同的偶数个小块。但是粗心的服务员将披萨切成了每块大小都完全不同奇数块,且肉眼能分辨出大小。 由于两人都想吃到最多的披萨,他们商量了一个他们认…...

uniapp 中video标签视频禁止快,拖拽快进
废话不多说,直接上代码 <video id"myVideo" :src"sectionInfo.type_config.video_url" timeupdate"bindtimeupdate"></video> <script>export default {data() {return {historyTime: 0,}},methods:{// 监听播放进…...
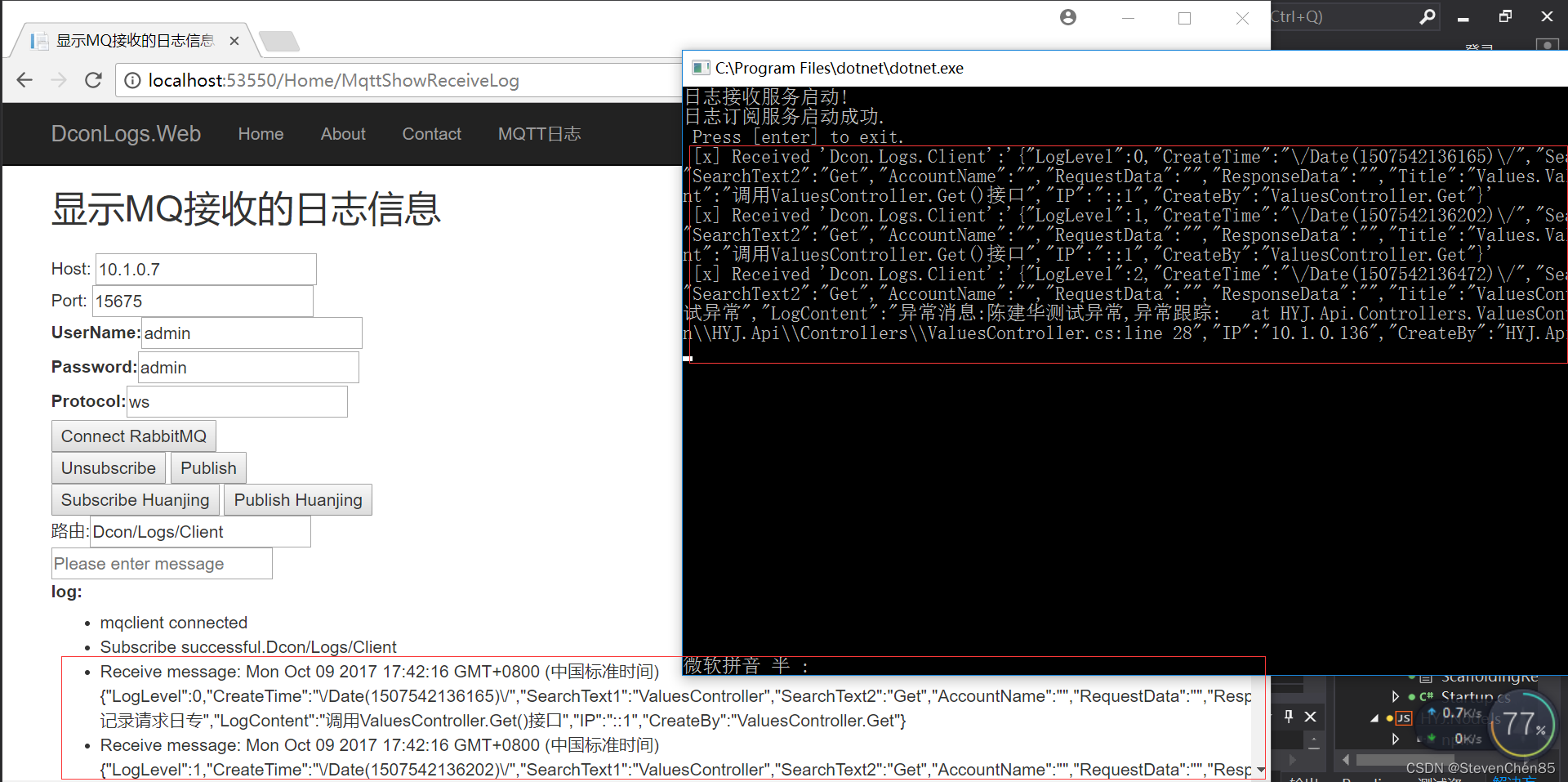
网页端HTML使用MQTTJs订阅RabbitMQ数据
最近在做一个公司的日志组件时有一个问题难住了我。今天问题终于解决了。由于在解决问题中,在网上也查了很多资料都没有一个完整的实例可以参考。所以本着无私分享的目的记录一下完整的解决过程和实例。 需求:做一个统一日志系统可以查看日志列表和一个可…...

课题学习(二十一)----姿态更新的四元数算法推导
声明:本人水平有限,博客可能存在部分错误的地方,请广大读者谅解并向本人反馈错误。 最近需要使用AEKF对姿态进行结算,所以又对四元数进了深入的学习,本篇博客仅对四元数进行推导,后续会对基于四元数的…...

NL2SQL进阶系列(5):论文解读业界前沿方案(DIN-SQL、C3-SQL、DAIL-SQL、SQL-PaLM)、新一代数据集BIRD-SQL解读
NL2SQL进阶系列(5):论文解读业界前沿方案(DIN-SQL、C3-SQL、DAIL-SQL)、新一代数据集BIRD-SQL解读 NL2SQL基础系列(1):业界顶尖排行榜、权威测评数据集及LLM大模型(Spider vs BIRD)全面对比优劣分析[Text2…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...
