如何在Python中使用matplotlib库进行数据可视化?
如何在Python中使用matplotlib库进行数据可视化?
在Python中使用matplotlib库进行数据可视化
数据可视化是将数据以图形或图像的形式展示出来的过程,它有助于我们更好地理解和分析数据。在Python中,matplotlib是一个非常受欢迎的数据可视化库,它提供了大量的函数和方法来绘制各种图表。
一、matplotlib的基本用法
在使用matplotlib进行数据可视化之前,需要先安装该库。可以通过pip命令进行安装:
bash复制代码
pip install matplotlib |
安装完成后,就可以在Python脚本中导入matplotlib库了:
python复制代码
import matplotlib.pyplot as plt |
matplotlib库的核心是pyplot模块,它提供了一套类似于MATLAB的命令式API,用于绘制各种图表。
二、绘制简单图表
- 绘制折线图
折线图通常用于展示数据随时间或其他连续变量的变化趋势。下面是一个简单的折线图绘制示例:
python复制代码
# 准备数据 | |
x = [1, 2, 3, 4, 5] | |
y = [2, 4, 6, 8, 10] | |
# 创建图表 | |
plt.plot(x, y) | |
# 设置标题和坐标轴标签 | |
plt.title('Simple Line Plot') | |
plt.xlabel('X-axis') | |
plt.ylabel('Y-axis') | |
# 显示图表 | |
plt.show() |
- 绘制柱状图
柱状图通常用于比较不同类别之间的数据大小。下面是一个柱状图绘制示例:
python复制代码
# 准备数据 | |
categories = ['A', 'B', 'C', 'D'] | |
values = [10, 15, 7, 10] | |
# 创建图表 | |
plt.bar(categories, values) | |
# 设置标题和坐标轴标签 | |
plt.title('Bar Chart') | |
plt.xlabel('Categories') | |
plt.ylabel('Values') | |
# 显示图表 | |
plt.show() |
三、自定义图表样式
matplotlib提供了丰富的选项来自定义图表的样式,包括线条样式、颜色、标记等。下面是一个自定义折线图的示例:
python复制代码
# 准备数据 | |
x = [1, 2, 3, 4, 5] | |
y = [2, 4, 1, 8, 10] | |
# 创建图表 | |
plt.plot(x, y, linestyle='--', color='red', marker='o') | |
# 设置标题和坐标轴标签 | |
plt.title('Customized Line Plot') | |
plt.xlabel('X-axis') | |
plt.ylabel('Y-axis') | |
# 显示网格 | |
plt.grid(True) | |
# 显示图例(如果使用了不同的线条样式、颜色或标记) | |
# plt.legend() | |
# 显示图表 | |
plt.show() |
在这个示例中,我们通过linestyle参数设置了线条样式为虚线,color参数设置了线条颜色为红色,marker参数设置了数据点的标记为圆圈。此外,我们还使用了plt.grid(True)来显示网格线,以便更好地观察数据的分布情况。
四、多图展示与子图布局
如果需要在一个窗口中展示多个图表,可以使用subplot函数来创建子图。下面是一个创建2x2子图布局的示例:
python复制代码
# 创建2x2的子图布局 | |
plt.subplot(2, 2, 1) # 第一个子图,位置(行, 列, 索引) | |
plt.plot(x, y) | |
plt.title('Plot 1') | |
plt.subplot(2, 2, 2) # 第二个子图 | |
plt.bar(categories, values) | |
plt.title('Plot 2') | |
plt.subplot(2, 2, 3) # 第三个子图 | |
plt.scatter(x, y) | |
plt.title('Plot 3') | |
plt.subplot(2, 2, 4) # 第四个子图 | |
plt.hist(y, bins=5) | |
plt.title('Plot 4') | |
# 显示所有子图 | |
plt.tight_layout() # 调整子图间的间距,防止重叠 | |
plt.show() |
在这个示例中,我们使用plt.subplot函数来创建子图,并指定每个子图的位置和索引。然后,在每个子图上绘制不同的图表类型。最后,使用plt.tight_layout函数来调整子图之间的间距,防止它们重叠。
相关文章:

如何在Python中使用matplotlib库进行数据可视化?
如何在Python中使用matplotlib库进行数据可视化? 在Python中使用matplotlib库进行数据可视化 数据可视化是将数据以图形或图像的形式展示出来的过程,它有助于我们更好地理解和分析数据。在Python中,matplotlib是一个非常受欢迎的数据可视化…...

网工基础协议——TCP/UDP协议
TCP和UDP的不同点: TCP(Transmission Control Protocol,传输控制协议); UDP(User Data Protocol,用户数据报协议); TCP:传输控制协议,面向连接可靠的协议,只能适用于单播通信&…...
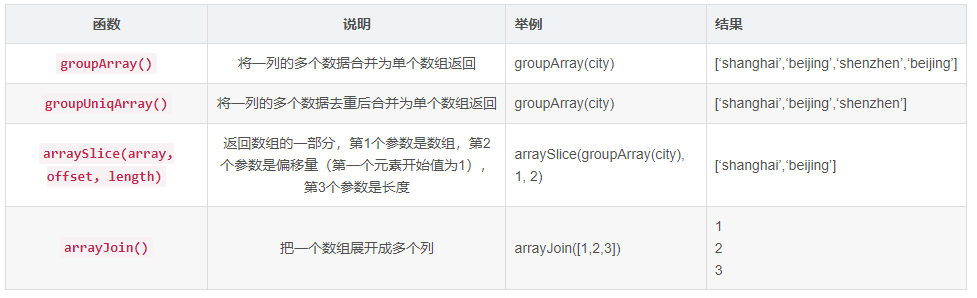
ClickHouse--16--普通函数
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 一、日期函数1、时间或日期截取函数(返回非日期)2、时间或日期截取函数(返回日期)3、日期或时间日期生成函数 二、类…...

03-JAVA设计模式-组合模式
组合模式 什么是组合模式 组合模式(Composite Pattern)允许你将对象组合成树形结构以表示“部分-整体”的层次结构,使得客户端以统一的方式处理单个对象和对象的组合。组合模式让你可以将对象组合成树形结构,并且能像单独对象一…...

C++发票识别、发票查验接口示例,您的“发票管理专家”
发票识别发票查验接口。当财务人员在进行发票的数字化管理时,仅需一键上传发票图片,翔云发票识别接口即可快速、精准对发票的全票面信息进行提取,翔云发票查验接口可根据识别接口提取的发票信息实时联网进行真伪查验。助财务工作者从发票海洋…...

【电控笔记6.2】拉式转换与转移函数
概要 laplace:单输入单输出,线性系统 laplace 传递函数 总结...

第十五届蓝桥杯题解-数字接龙
题意:经过所有格子,并且不能进行交叉,走的下一个格子必须是当前格子值1%k,输出路径最小的那一条(有8个方向,一会粘图) 思路:按照8个方向设置偏移量进行dfs,第一个到达终…...
【vue】绑定事件 v-on
v-on 简写: clickkeyupkeydownkeyup.wkeyup.ctrl.a <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><…...
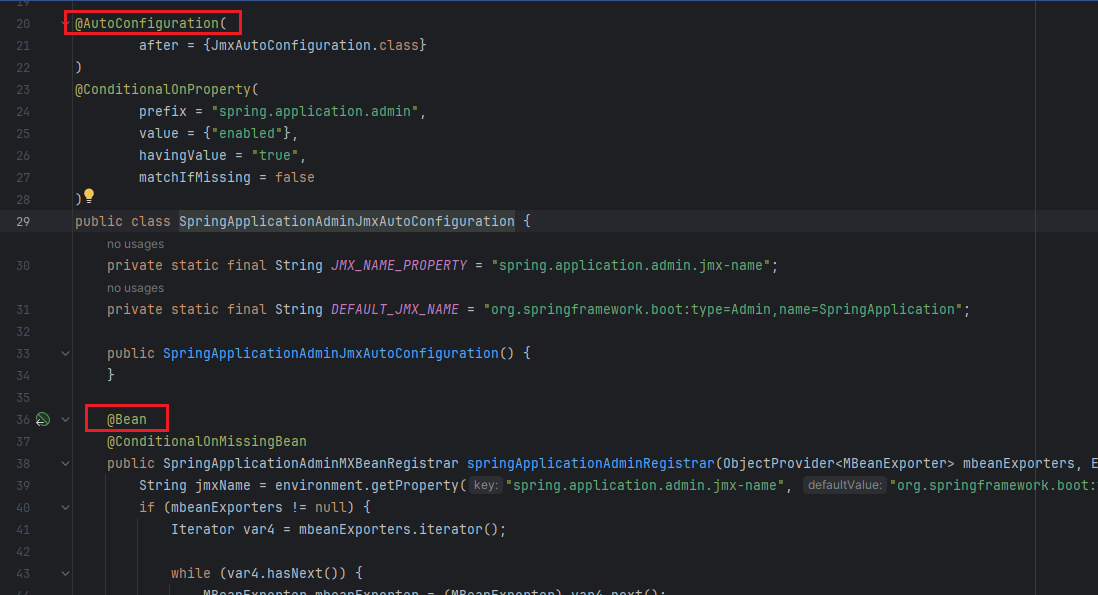
【应用】SpringBoot-自动配置原理
前言 本文简要介绍SpringBoot的自动配置原理。 本文讲述的SpringBoot版本为:3.1.2。 前置知识 在看原理介绍之前,需要知道Import注解的作用: 可以导入Configuration注解的配置类、声明Bean注解的bean方法;可以导入ImportSele…...

中文编程入门(Lua5.4.6中文版)第十二章 Lua 协程 参考《愿神》游戏
在《愿神》的提瓦特大陆上,每一位冒险者都拥有自己的独特力量——“神之眼”,他们借助元素之力探索广袤的世界,解决谜题,战胜敌人。而在提瓦特的科技树中,存在着一项名为“协同程序”的高级秘术,它使冒险者…...

C++笔记之注册回调函数常见的5种情况对比
C++笔记之注册回调函数常见的5种情况对比 —— 2024-04-10 code review! 文章目录 C++笔记之注册回调函数常见的5种情况对比1.五种情况2.示例2.1. `RegisterCallback` 和 `Callback` 都是普通函数2.2. `RegisterCallback` 是成员函数,`Callback` 是普通函数2.3. `RegisterC…...

人工智能揭示矩阵乘法的新可能性
人工智能揭示矩阵乘法的新可能性 数学家酷爱漂亮的谜题。当你尝试找到最有效的方法时,即使像乘法矩阵(二维数字表)这样抽象的东西也会感觉像玩一场游戏。这有点像尝试用尽可能少的步骤解开魔方——具有挑战性,但也很诱人。除了魔方…...

实在智能携手长江新零售俱乐部:探秘实在Agent数字员工,开启零售品牌增长新篇章
近日,实在智能携手长江新零售俱乐部成功举办了“AIGC:数字员工助力零售品牌新增长”主题活动,成功吸引了二十余家企业中高层管理精英的踊跃参与。在此次活动中,与会者围绕零售业数字化转型的当前态势、面临的挑战及其重要性进行了…...

计算机科学与导论 第十七 十八章 计算理论,人工智能
文章预览: 计算理论17.1 引言17.2 简单语言17.3 图灵机邱奇 -图灵 论题 人工智能引言18.1.1 什么是人工智能18.1.2 智能体18.1.3 编程语言 18.2 知识的表示18.2.1 语义网18.2.2 框架18.2.3 谓词逻辑18.2.4 基于规则的系统 18.2 专家系统18.3 语言理解18.4 搜索18.5 …...
linux 设置定时任务---学习
1、设置定时任务 crontab -e 设置格式参考:【Linux】Linux crontab 命令定时任务设置_crontab 设置每天10:30执行-CSDN博客 测试过程: */1 * * * * /root/cronjob.sh 脚本内容: echo "hell0 cronjob" >> /root/test/hello.txt 实现…...

钡铼IOy系列模块深挖工业场景需求提供丰富多样的I/O解决方案
钡铼IOy系列模块以其灵活性和多样性,在工业场景中提供了丰富多样的I/O解决方案,满足了不同行业、不同应用场景的需求。以下是一些常见的工业场景需求及钡铼IOy系列模块提供的解决方案: 1. 工厂自动化 需求:工厂自动化需要对生产线…...

【刷题笔记】第三天
两道简单题 文章目录 [2923. 找到冠军 I](https://leetcode.cn/problems/find-champion-i/description/)[3095. 或值至少 K 的最短子数组 I](https://leetcode.cn/problems/shortest-subarray-with-or-at-least-k-i/description/) 2923. 找到冠军 I 方法1: 如果 i …...
开源模型应用落地-LangChain试炼-CPU调用QWen1.5(一)
一、前言 尽管现在的大语言模型已经非常强大,可以解决许多问题,但在处理复杂情况时,仍然需要进行多个步骤或整合不同的流程才能达到最终的目标。然而,现在可以利用langchain来使得模型的应用变得更加直接和简单。 通过langchain框…...
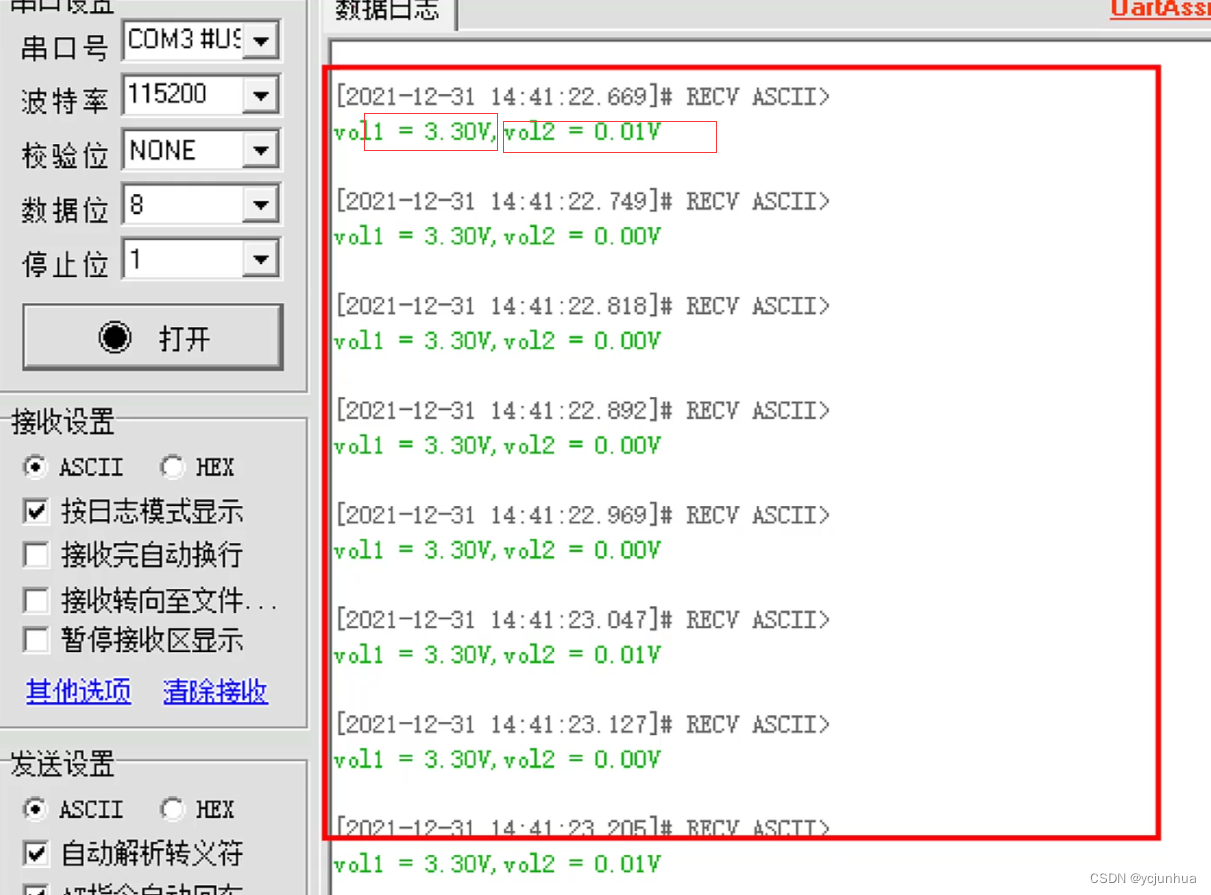
STM32-模数转化器
ADC(Analog-to-Digital Converter) 指模数转换器。是指将连续变化的模拟信号转换 为离散的数字信号的器件。 ADC相关参数说明: 分辨率: 分辨率以二进制(或十进制)数的位数来表示,一般有 8 位、10 位、12 位、16 位…...

算法刷题记录2
4.图 4.1.被围绕的区域 思路:图中只有与边界上联通的O才不算是被X包围。因此本题就是从边界上的O开始递归,找与边界O联通的O,并标记为#(代表已遍历),最后图中剩下的O就是:被X包围的O。图中所有…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...

跨平台商品数据接口的标准化与规范化发展路径:淘宝京东拼多多的最新实践
在电商行业蓬勃发展的当下,多平台运营已成为众多商家的必然选择。然而,不同电商平台在商品数据接口方面存在差异,导致商家在跨平台运营时面临诸多挑战,如数据对接困难、运营效率低下、用户体验不一致等。跨平台商品数据接口的标准…...
