基于SpringBoot+Vue的装饰工程管理系统(源码+文档+包运行)
一.系统概述
如今社会上各行各业,都喜欢用自己行业的专属软件工作,互联网发展到这个时候,人们已经发现离不开了互联网。新技术的产生,往往能解决一些老技术的弊端问题。因为传统装饰工程项目信息管理难度大,容错率低,管理人员处理数据费工费时,所以专门为解决这个难题开发了一个装饰工程管理系统——项目立项子系统,可以解决许多问题。
装饰工程管理系统——项目立项子系统可以实现合同信息管理,合同报价管理,客户管理,立项项目管理,公告信息管理,员工管理,预算报价管理,装饰材料总计划管理,装修进度管理等功能。该系统采用了Mysql数据库,Java语言,Spring Boot框架等技术进行编程实现。
装饰工程管理系统——项目立项子系统可以提高装饰工程项目信息管理问题的解决效率,优化装饰工程项目信息处理流程,保证装饰工程项目信息数据的安全,它是一个非常可靠,非常安全的应用程序。
二.技术环境
jdk版本:1.8 及以上
ide工具:Eclipse或者 IDEA
数据库: mysql5.7
编程语言: Java
java框架:SpringBoot
maven: 3.6.1
详细技术:HTML+CSS+JAVA+SpringBoot+MYSQL+VUE+MAVEN
三.功能设计
装饰工程管理系统——项目立项子系统可以实现合同信息管理,合同报价管理,客户管理,立项项目管理,公告信息管理,员工管理,预算报价管理,装饰材料总计划管理,装修进度管理等功能。
下图即为管理员用例图,管理员权限操作的功能包括管理合同信息,管理合同报价,管理立项项目,管理预算报价,管理装修进度,管理员工,管理客户等信息。

下图即为员工用例图,员工权限操作的功能包括对合同信息,合同报价信息,立项项目信息,预算报价信息,装饰材料总计划信息,装修进度信息等进行新增并管理。

下图即为客户用例图,客户权限操作的功能包括查看合同报价,查看合同信息,查看立项项目,查看预算报价,查看装修进度,查看公告信息等。

下图即为设计的管理员功能结构,管理员权限操作的功能包括管理合同信息,管理合同报价,管理立项项目,管理预算报价,管理装修进度,管理员工,管理客户等信息。

下图即为设计的员工功能结构,员工权限操作的功能包括对合同信息,合同报价信息,立项项目信息,预算报价信息,装饰材料总计划信息,装修进度信息等进行新增并管理。

下图即为设计的客户功能结构,客户权限操作的功能包括查看合同报价,查看合同信息,查看立项项目,查看预算报价,查看装修进度,查看公告信息等。

本程序在设计结构选择上首选B/S,也是为了满足程序今后升级便利,以及程序低维护成本的要求。本程序的网络拓扑设计也会在下图展示,通过图形的方式来描述更容易理解。

四.系统实现效果
管理员功能实现
下图即为编码实现的立项项目管理界面,立项项目信息包括项目名称,项目文件,项目类型等信息,管理员审核立项项目信息,下载立项项目文件,查询立项项目信息等。

下图即为编码实现的合同报价管理界面,合同报价信息包括合同详情,报价金额,合同标题等信息,管理员可以修改合同报价信息,删除需要删除的合同报价信息等。

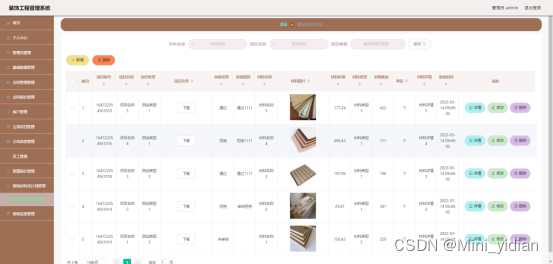
下图即为编码实现的装饰材料总计划管理界面,装饰材料总计划信息包括材料名称,材料价格,材料采购数量,材料详情等信息,管理员可以修改装饰材料总计划信息,可以查询装饰材料总计划信息,可以删除装饰材料总计划信息等。
下图即为编码实现的客户管理界面,客户信息包括联系方式,姓名,性别等信息,管理员可以删除需要删除的客户信息,可以查询客户等。

员工功能实现
下图即为编码实现的新增立项项目界面,员工在新增立项项目界面中登记立项项目信息,主要包括客户姓名,联系方式,项目类型,项目文件等信息,登记完成立项项目信息之后,直接提交。

下图即为编码实现的预算报价管理界面,员工可以新增预算报价信息,可以查看预算报价详细信息。
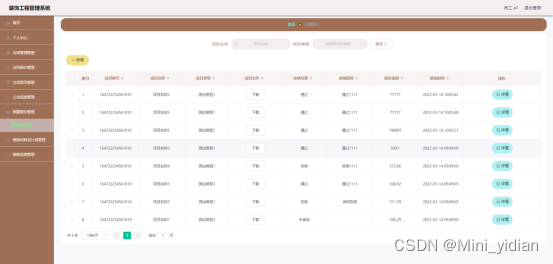
下图即为编码实现的合同信息管理界面,员工新增项目合同信息,下载项目文件,下载合同文件,查看合同详细信息等。

客户功能实现
下图即为编码实现的装修进度查看界面,客户自己在装修进度查看界面查看装修进度图片,装修进度详情信息,可以通过装修进度标题查询装修进度信息,也能根据项目名称查询装修进度信息等。

下图即为编码实现的合同报价查看界面,客户查看合同报价金额,查看合同详情,下载合同文件。

下图即为编码实现的装饰材料总计划查看界面,客户查看材料价格,材料图片,采购数量,材料详情,材料名称等信息,可以查看装饰材料总计划详情信息,同时可以根据材料名称或项目名称来查询装饰材料总计划信息等。

论文目录
目 录
摘 要 I
Abstract II
第1章 绪论 1
1.1 课题背景 1
1.2 课题意义 1
1.3 研究内容 1
第2章 开发环境与技术 3
2.1 Java语言 3
2.2 MYSQL数据库 3
2.3 IDEA开发工具 4
2.4 Spring Boot框架 4
第3章 系统分析 5
3.1 可行性分析 5
3.1.1 技术可行性 5
3.1.2 经济可行性 5
3.1.3 操作可行性 5
3.2 系统流程 5
3.2.1 操作流程 6
3.2.2 登录流程 6
3.2.3 删除信息流程 7
3.2.4 添加信息流程 7
3.3 性能需求 8
3.4 功能需求 9
第4章 系统设计 13
4.1 功能结构设计 13
4.2 数据库设计 15
4.2.1 数据库概念设计 15
4.2.2 数据库物理设计 18
第5章 系统实现 23
5.1 管理员功能实现 23
5.1.1 立项项目管理 23
5.1.2 合同报价管理 23
5.1.3 装饰材料总计划管理 24
5.1.4 客户管理 24
5.2 员工功能实现 25
5.2.1 新增立项项目 25
5.2.2 预算报价管理 25
5.2.3 合同信息管理 26
5.3 客户功能实现 26
5.3.1 装修进度查看 26
5.3.2 合同报价查看 27
5.3.3 装饰材料总计划查看 27
第6章 系统测试 29
6.1 功能测试 29
6.1.1 登录功能测试 29
6.1.2 修改密码功能测试 30
6.2 系统测试结果 31
结 论 32
参考文献 33
致 谢 34
此源码非开源,若需要此源码可扫码添加微信进行咨询!

相关文章:

基于SpringBoot+Vue的装饰工程管理系统(源码+文档+包运行)
一.系统概述 如今社会上各行各业,都喜欢用自己行业的专属软件工作,互联网发展到这个时候,人们已经发现离不开了互联网。新技术的产生,往往能解决一些老技术的弊端问题。因为传统装饰工程项目信息管理难度大,容错率低&a…...

vue3中axios添加请求和响应的拦截器
本章主要是以记录为主。 在src创建一个utils文件夹,并在utils中创建一个request.js文件。 // 引入axios import axios from "axios"; // import qs from "qs"; // 创建axios实例 const instance axios.create(); // 请求拦截器 instance.int…...
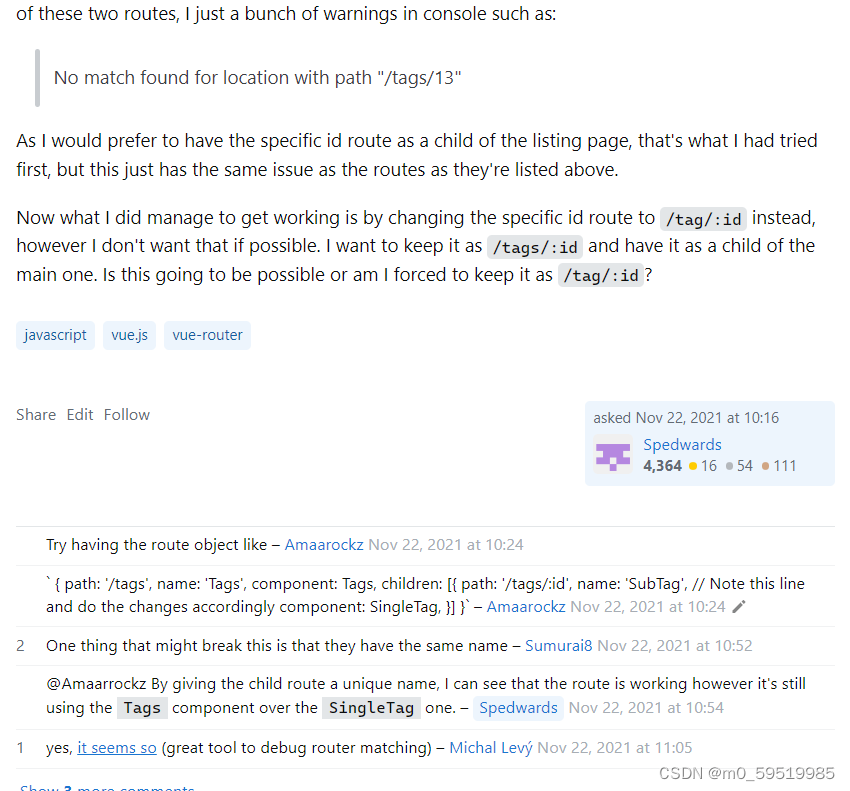
<router-link>出现Error: No match for {“name“:“home“,“params“:{}}
在将<a></a>标签换到<router-link></router-link>的时候出现No match for {"name":"home","params":{}}这样的错误,其中格式并无错误, <router-link class"navbar-brand active" …...
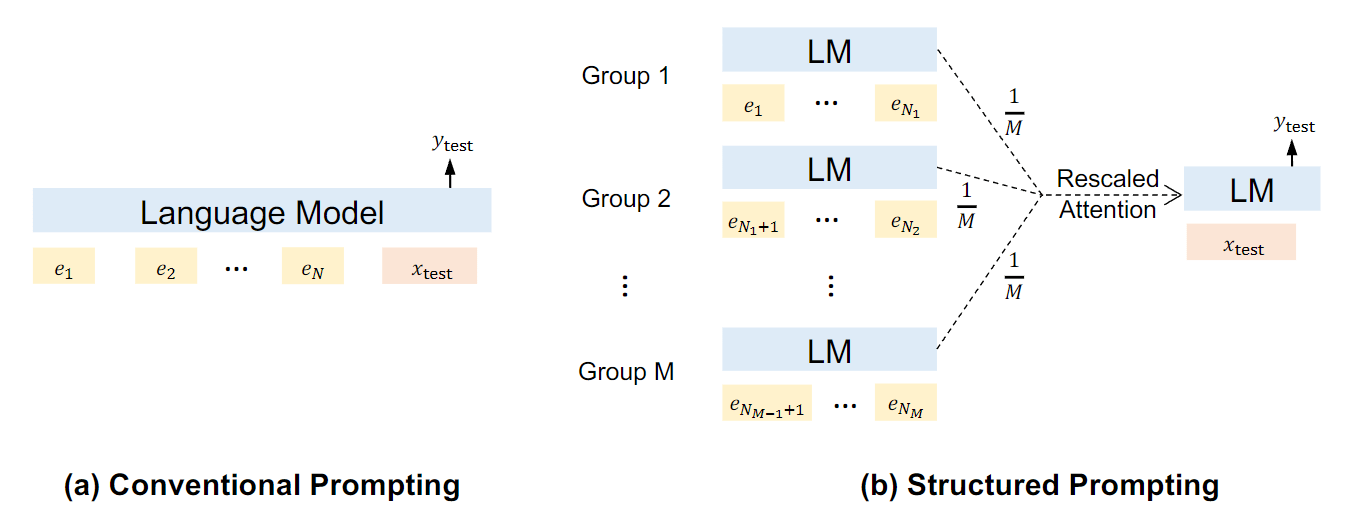
prompt 工程整理(未完、持续更新)
工作期间会将阅读的论文、一些个人的理解整理到个人的文档中,久而久之就积累了不少“个人”能够看懂的脉络和提纲,于是近几日准备将这部分略显杂乱的内容重新进行梳理。论文部分以我个人的理解对其做了一些分类,并附上一些简短的理解…...

兼容性测试用例
备注:本文为博主原创文章,未经博主允许禁止转载。如有问题,欢迎指正。 个人笔记(整理不易,有帮助,收藏+点赞+评论,爱你们!!!你的支持是我写作的动力) 笔记目录:学习笔记目录_pytest和unittest、airtest_weixin_42717928的博客-CSDN博客 个人随笔:工作总结随笔_8、…...
阿里云4核8G云服务器价格多少钱?700元1年
阿里云4核8G云服务器价格多少钱?700元1年。阿里云4核8G服务器租用优惠价格700元1年,配置为ECS通用算力型u1实例(ecs.u1-c1m2.xlarge)4核8G配置、1M到3M带宽可选、ESSD Entry系统盘20G到40G可选,CPU采用Intel(R) Xeon(R…...

ts 中的keyof 和typeof
作用: keyof:用于获取对象类型的所有键的联合类型。typeof:用于获取变量或表达式的类型。 返回类型: keyof:返回的是一个对象类型的所有键组成的联合类型。typeof:返回的是一个值的类型。 使用场景…...

每日一题:买卖股票的最佳时机II
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。 在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。 返回 你能获得的 最大 利润 。 示例 1&a…...
nginx安装在linux上
nginx主要用于反向代理和负载均衡,现在简单的说说如何在linux操作系统上安装nginx 第一步:安装依赖 yum install -y gcc-c pcre pcre-devel zlib zlib-devel openssl openssl-devel 第二步: 下载nginx,访问官网,ngin…...
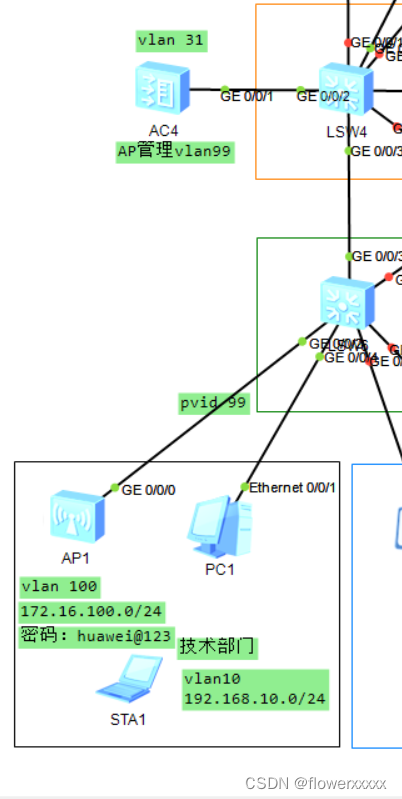
ENSP-旁挂式AC
提醒:如果AC不能成功上线AP,一般问题不会出在AC上,优先关注AC-AP线路上的二层或三层组网的三层交换机 拓扑图 管理VLAN:99 | 业务VLAN:100 注意点: 1.连接AP的接口需要打上pvid为管理vlan的标签 2.AC和…...

如何获取手机root权限?
获取手机的 root 权限通常是指在 Android 设备上获取超级用户权限,这样用户就可以访问和修改系统文件、安装定制的 ROM、管理应用权限等。然而,需要注意的是,获取 root 权限可能会导致手机失去保修、安全性降低以及使系统变得不稳定。在获取 …...
海南赛区复赛真题)
2023年全国青少年信息素养大赛(Python)海南赛区复赛真题
2023年全国青少年信息素养大赛(Python)海南赛区复赛真题第1题,整数加8 题目描述: 输入一个整数,输出这个整数加8 的结果。 输入描述: 输入一行一个正整数。 输出描述: 输出求和的结果。 样例1: 输入: 5 输出: 13 x= int(input()) print(x+8) 第2题,哼哈二将 题目描…...

node.js服务器动态资源处理
一、node.js服务器动态资源处理与静态资源处理的区别? 静态与动态服务器主要区别于是否读取数据库,若然在数据库中的资料处理中将数据转换成可取用格式的结构,也就是说把对象转化为可传输的字节序列过程称为序列化,反之则为反序列…...

DNS是TCP还是UDP
既使用TCP也使用UDP 1. 域名解析时用UDP 在大多数情况下,DNS请求使用UDP协议,因为UDP协议可以提供较高的效率和安全性,尤其是在查询的响应大小较小(通常不超过512字节)时。非可靠连接,因为传输的数据量小…...
)
Redis魔法:解锁高性能缓存的神奇之门(二)
本系列文章简介: 在现代的软件开发中,高性能和高可用性是每个开发者都追求的目标。然而,随着数据量和访问频率的不断增长,传统的数据库存储方案往往难以应对这种挑战。这就引出了一个问题:如何在保证数据的高效访问和持…...
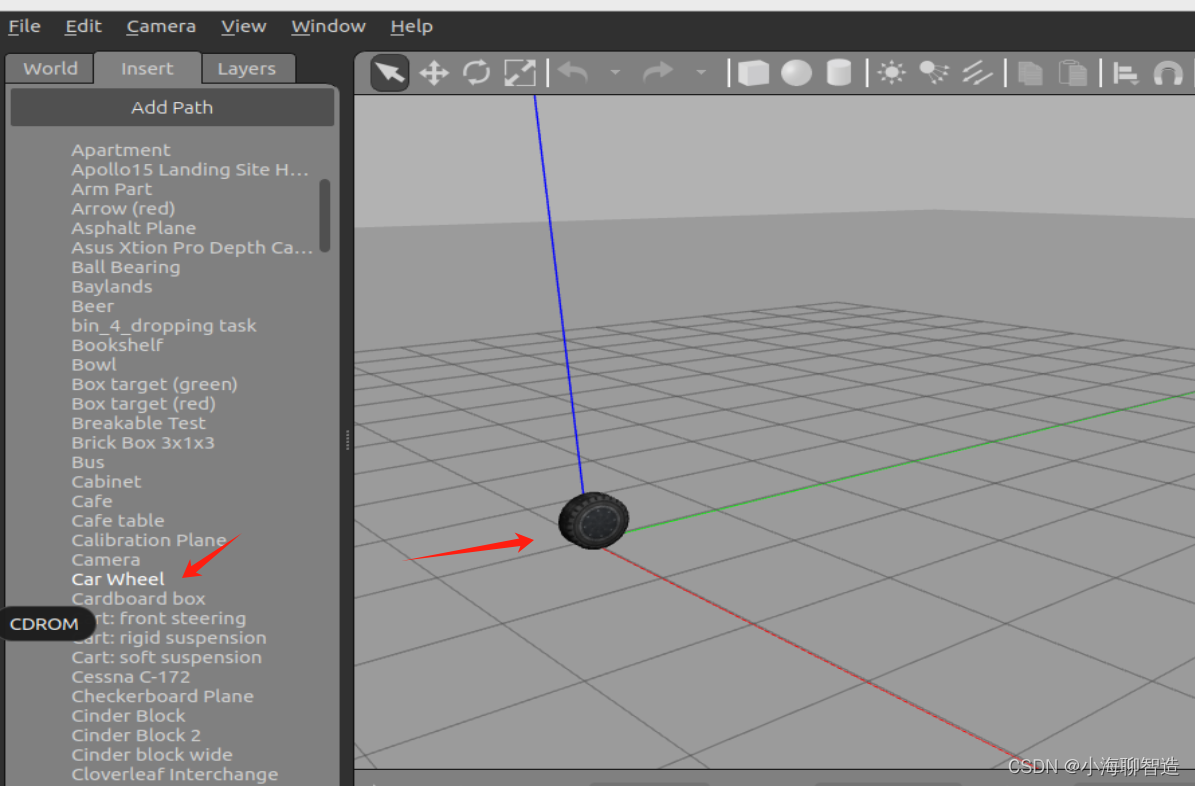
ROS2 仿真学习02 Gazebo导入官方示例模型
1.下载模型 git clone https://gitee.com/bingda-robot/gazebo_models.git将gazebo_models拖到到.gazebo当中(如果没看到.gazebo文件请按住CTRLh) 2.添加模型到gazebo的Insert 这就将官方示例的模型都导入到Gazebo 了 随便试试一个模型...

echarts图表按需导入
引入核心包引入图表类型引入使用组件引入渲染器注册所有引入 在项目中引入 Apache ECharts // 引入 echarts 核心模块,核心模块提供了 echarts 使用必须要的接口。 import * as echarts from echarts/core; // 引入柱状图图表,图表后缀都为 Chart impo…...

蓝桥杯(基础题)
试题 C: 好数 时间限制 : 1.0s 内存限制: 256.0MB 本题总分:10 分 【问题描述】 一个整数如果按从低位到高位的顺序,奇数位(个位、百位、万位 )上 的数字是奇数,偶数位(十位、千位、十万位 &…...
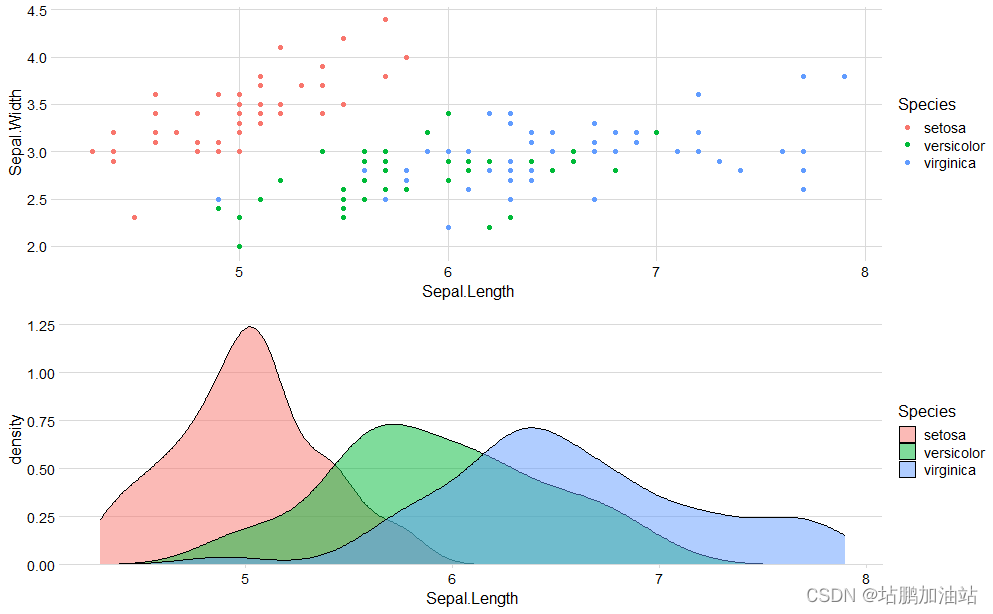
【R语言】概率密度图
概率密度图是用来表示连续型数据的分布情况的一种图形化方法。它通过在数据的取值范围内绘制一条曲线来描述数据的分布情况,曲线下的面积代表了在该范围内观察到某一数值的概率。具体来说,对于给定的连续型数据,概率密度图会使用核密度估计&a…...

【学习】软件测试需求分析要从哪些方面入手
软件测试需求分析是软件测试过程中非常重要的一个环节,它是为了明确软件测试的目标、范围、资源和时间等要素,以确保软件测试的有效性和全面性。本文将从以下几个方面对软件测试需求分析进行详细的阐述: 一、软件测试目标 软件测试目标是指…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...
