【机器学习300问】74、如何理解深度学习中L2正则化技术?
深度学习过程中,若模型出现了过拟合问题体现为高方差。有两种解决方法:
- 增加训练样本的数量
- 采用正则化技术
增加训练样本的数量是一种非常可靠的方法,但有时候你没办法获得足够多的训练数据或者获取数据的成本很高,这时候正则化技术就可以有效的帮助你避免模型过拟合。接下来本文就来讲解一下深度学习中的正则化起作用的原理(文中以L2正则化为例)。
有关正则化的基础知识,可以回看我之前的文章哦:
【机器学习300问】18、正则化是如何解决过拟合问题的?![]() http://t.csdnimg.cn/vX2mP
http://t.csdnimg.cn/vX2mP
一、包括L2正则化项的损失函数长什么样
在损失函数(如均方误差、交叉熵误差等)的基础上,L2正则化引入了一个与权重向量W相关的正则化项,通常表示为:
| 符号 | 解释 |
| 包含正则化项的总损失函数 | |
| 代表未加正则化项的原始损失函数,这通常是对每个样本的损失的平均值,如交叉熵损失或均方误差损失 | |
| 分别表示网络中的权重和偏置参数 | |
| 正则化项的系数,这是一个超参数,用于控制正则化的强度 | |
| 训练样本的数量 | |
| L2正则化项,通常称为权重衰减项。是所有权重矩阵的Frobenius范数的平方的和。Frobenius范数是一个矩阵范数,等同于矩阵元素的平方和的平方根 | |
表示第 |
二、L2正则化的作用机制
(1)权重缩小
在优化过程中,由于L2正则化项的存在,当模型试图降低原始损失时,同时需要考虑减小权重的平方和。这会促使模型在训练过程中选择较小的权重值,避免权重值过大导致模型对训练数据的过度敏感。
(2)防止过拟合
较小的权重值意味着模型对单个特征的影响不会过于突出,减少了模型对训练数据中噪声和个别样本特性的过度学习,有利于提高模型在未见过数据上的泛化能力。
三、L2正则化到底是怎么起作用的嘛!
(1)微观上,对激活函数的影响
激活函数tanh(双曲正切函数)的输出范围在-1到1之间,形状类似于Sigmoid函数但更为平缓,且在两端饱和区的梯度更接近于0。公式就不赘述了之前的文章详细介绍过了,我们在这里只关注函数的图像,从图像上理解就可以了。

用表示,那么我们发现,只要
非常小,如果
只涉及少量参数,我们就只利用了双曲正切函数的线性状态,如下图所示:

当L2正则化惩罚过大时,模型的权重被迫保持较小的值,也就是说也会很小。对于tanh激活函数意味着:
- tanh函数接近线性(斜率为1),较小的权重导致输入信号大部分位于tanh函数的线性区域内,使得模型的非线性表达能力减弱,趋向于线性模型。
- 过强的L2正则化可能会限制tanh激活函数充分发挥其非线性变换的能力,尤其是对于需要捕捉复杂非线性关系的任务,模型可能无法有效学习数据的深层次结构。
在之前的文章中讲到过,如果激活函数都是线性函数,那么无论你的神经网络有多深,节点有很多,都相当于一个简单的线性模型。这就是为什么L2正则化通过约束权重的大小,间接降低了模型的复杂度。
(2)宏观上,对神经网络结构的影响
现在我们假设一种很极端的情况,正则化参数非常大,因此对权重的惩罚非常大,导致权重很小,小到约等于0。因为公式
,我们如果不考虑偏置。就会得到
,这样一来从神经网络的在该节点的输出
。意味着这个神经元死亡了。如果用图来表示的话就是:
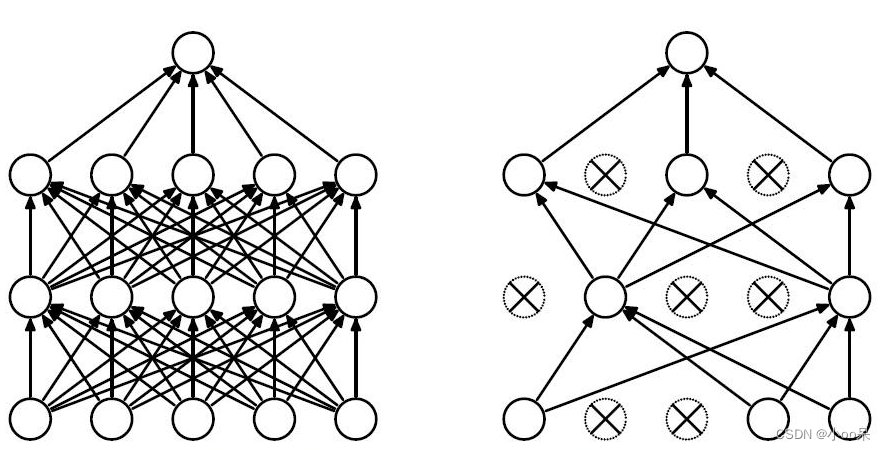
显然,模型的复杂度被降低了,提高模型的泛化能力。
相关文章:

【机器学习300问】74、如何理解深度学习中L2正则化技术?
深度学习过程中,若模型出现了过拟合问题体现为高方差。有两种解决方法: 增加训练样本的数量采用正则化技术 增加训练样本的数量是一种非常可靠的方法,但有时候你没办法获得足够多的训练数据或者获取数据的成本很高,这时候正则化技…...
)
C语言程序设计每日一练(4)
完全平方数 首先,我们需要明确什么是完全平方数。完全平方数是指一个整数,它可以表示为另一个整数的平方。例如,1、4、9、16等都是完全平方数,因为它们分别是1、2、3、4的平方。 现在,让我们回到这个问题。我们知道这…...

m4p转换mp3格式怎么转?3个Mac端应用~
M4P文件格式的诞生伴随着苹果公司引入FairPlay版权管理系统,该系统旨在保护音频的内容。M4P因此而生,成为受到FairPlay系统保护的音频格式,常见于苹果设备的iTunes等平台。 MP3文件格式的多个优点 MP3格式的优点显而易见。首先,其…...
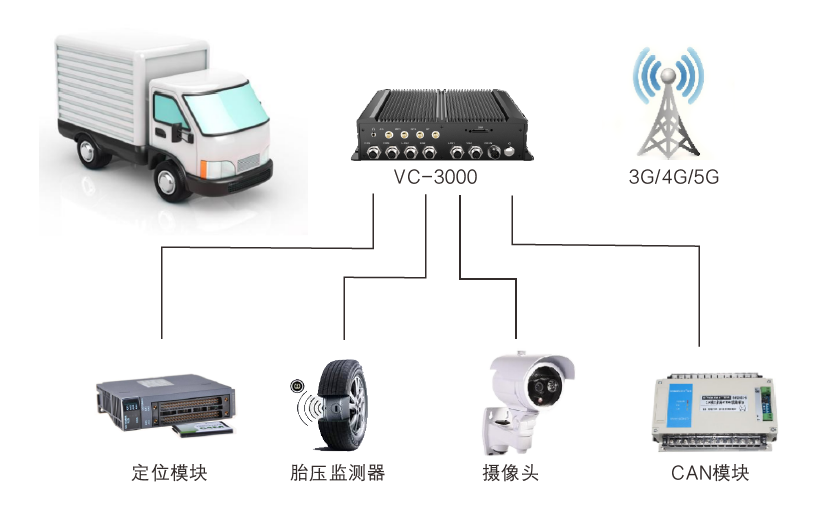
全国产化无风扇嵌入式车载电脑在车队管理嵌入式车载行业应用
车队管理嵌入式车载行业应用 车队管理方案能有效解决车辆繁多管理困难问题,配合调度系统让命令更加精确有效执行。实时监控车辆状况、行驶路线和位置,指导驾驶员安全有序行驶,有效降低保险成本、事故概率以及轮胎和零部件的磨损与损坏。 方…...

爬虫入门——Request请求
目录 前言 一、Requests是什么? 二、使用步骤 1.引入库 2.请求 3.响应 三.总结 前言 上一篇爬虫我们已经提及到了urllib库的使用,为了方便大家的使用过程,这里为大家介绍新的库来实现请求获取响应的库。 一、Requests是什么࿱…...
创建一个javascript公共方法的npm包,js-tool-big-box,发布到npm上,一劳永逸
前端javascript的公共方法太多了,时间日期的,数值的,字符串的,搞复制的,搞网络请求的,搞数据转换的,几乎就是每个新项目,有的拷一拷,没有的继续写,放个utils目…...
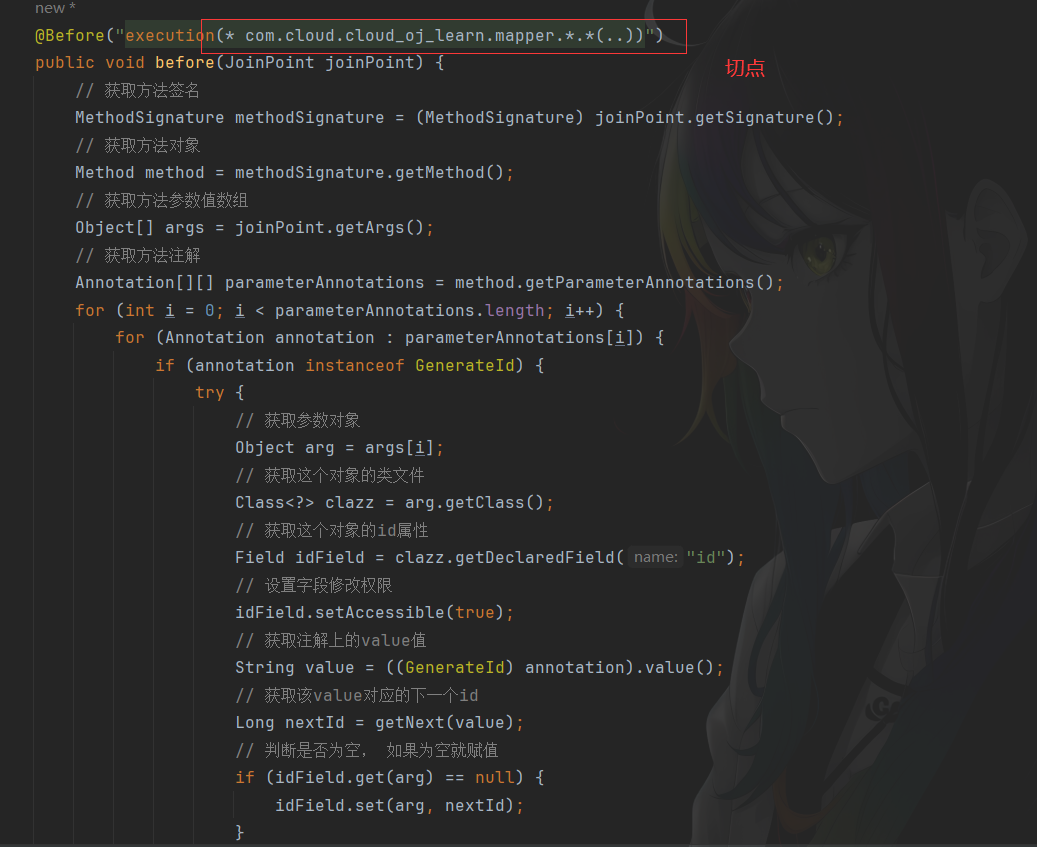
【在线OJ系统】自定义注解实现分布式ID无感自增
实现思路 首先自定义参数注解,然后根据AOP思想,找到该注解作用的切点,也就是mapper层对于mapper层的接口在执行前都会执行该aop操作:获取到对于的方法对象,根据方法对象获取参数列表,根据参数列表判断某个…...
35. UE5 RPG制作火球术技能
接下来,我们将制作技能了,总算迈进了一大步。首先回顾一下之前是如何实现技能触发的,然后再进入正题。 如果想实现我之前的触发方式的,请看此栏目的31-33篇文章,讲解了实现逻辑,这里总结一下: …...
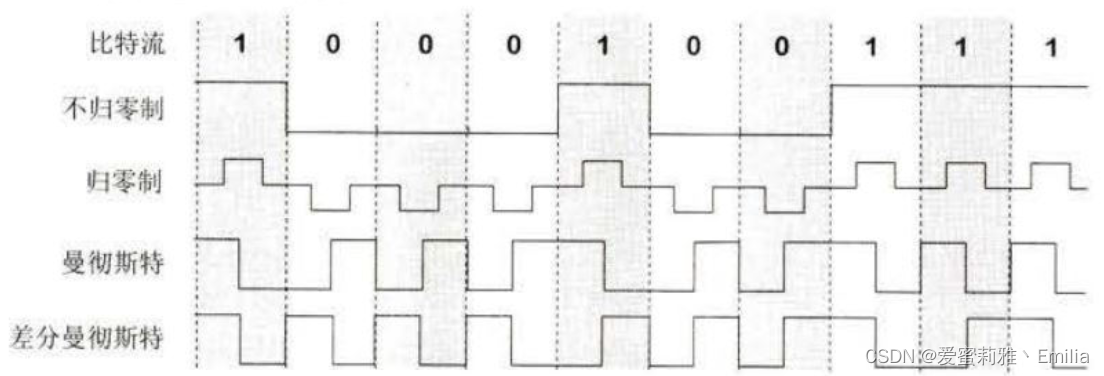
计算机网络 TCP/IP体系 物理层
一. TCP/IP体系 物理层 1.1 物理层的基本概念 物理层作为TCP/IP网络模型的最低层,负责直接与传输介质交互,实现比特流的传输。 要完成物理层的主要任务,需要确定以下特性: 机械特性:物理层的机械特性主要涉及网络…...
微服务相关
1. 微服务主要七个模块 中央管理平台:生产者、消费者注册,服务发现,服务治理,调用关系生产者消费者权限管理流量管理自定义传输协议序列化反序列化 2. 中央管理平台 生产者A在中央管理平台注册后,中央管理平台会给他…...
虚拟机下如何使用Docker(完整版)
Docker详细介绍: Docker 是一款开源的应用容器引擎,由Docker公司最初开发并在2013年发布。Docker的核心理念源自于操作系统级别的虚拟化技术,尤其是Linux上的容器技术(如LXC),它为开发人员和系统管理员提供…...

asp.net core 依赖注入后的服务生命周期
ASP.NET Core 依赖注入(DI)容器支持三种服务的生命周期选项,它们定义了服务实例的创建和销毁的时机。理解这三种生命周期对于设计健壯且高效的应用程序非常重要: 瞬时(Transient): 瞬时服务每次…...

交换排序:冒泡排序和快速排序
冒泡排序 思路 通过多次遍历数组,比较相邻的元素,并交换它们,使得每次遍历结束后,最大(或最小)的元素都“冒泡”到数组的末尾 实现 public class Main {public static void main(String[] args) {int[] …...

聊天机器人ChatGPT指导下的论文写作
ChatGPT无限次数:点击直达 聊天机器人ChatGPT指导下的论文写作 引言 随着人工智能技术的不断发展,聊天机器人在各个领域得到了广泛应用。其中,ChatGPT作为一个先进的自然语言处理模型,为各种文本生成任务提供了强大的支持。在学术界…...
康谋技术 | 深入探讨:自动驾驶中的相机标定技术
随着自动驾驶技术的快速发展,多传感器的数据采集和融合可以显著提高系统的冗余度和容错性,进而保证决策的快速性和正确性。在项目开发迭代过程中,传感器标定扮演着至关重要的角色,它位于数据采集平台与感知融合算法之间࿰…...

如何在 Ubuntu 上启用 IPv6
一、前提条件 一台安装了 Ubuntu 22.04 的计算机具有 sudo 权限的用户账户已连接到支持 IPv6 的网络 二、检查系统是否支持 IPv6 在启用 IPv6 之前,首先要确保您的系统支持 IPv6。要检查内核是否启用了 IPv6,可以运行以下命令: cat /proc/…...

Mac电脑上有什么好玩的格斗游戏 《真人快打1》可以在苹果电脑上玩吗
你是不是喜欢玩格斗游戏?你是不是想在你的Mac电脑上体验一些刺激和激烈的对战?在这篇文章中,我们将介绍Mac电脑上有什么好玩的格斗游戏,以及《真人快打1》可以在苹果电脑上玩吗。 一、Mac电脑上有什么好玩的格斗游戏 格斗游戏是…...
)
【leetcode面试经典150题】55. 逆波兰表达式求值(C++)
【leetcode面试经典150题】专栏系列将为准备暑期实习生以及秋招的同学们提高在面试时的经典面试算法题的思路和想法。本专栏将以一题多解和精简算法思路为主,题解使用C语言。(若有使用其他语言的同学也可了解题解思路,本质上语法内容一致&…...

云轴科技ZStack入选中国信通院《高质量数字化转型产品及服务全景图(2023年度)》
近日,由中国互联网协会主办、中国信通院承办的“2024高质量数字化转型创新发展大会”暨“铸基计划”年度会议在北京成功召开。 本次大会发布了2024年度行业数字化转型趋势,总结并展望了“铸基计划”2023年取得的工作成果及2024年的工作规划。同时&#…...

Workerman开启ssl方法如下
参考地址 Workerman开启ssl方法如下-遇见你与你分享 准备工作: 1、Workerman版本不小于3.3.7 2、PHP安装了openssl扩展 3、已经申请了证书(pem/crt文件及key文件)放在了/etc/nginx/conf.d/ssl下 4、配置文件 location /wss { proxy_set…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...

Vue3 PC端 UI组件库我更推荐Naive UI
一、Vue3生态现状与UI库选择的重要性 随着Vue3的稳定发布和Composition API的广泛采用,前端开发者面临着UI组件库的重新选择。一个好的UI库不仅能提升开发效率,还能确保项目的长期可维护性。本文将对比三大主流Vue3 UI库(Naive UI、Element …...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...

python打卡day49@浙大疏锦行
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 一、通道注意力模块复习 & CBAM实现 import torch import torch.nn as nnclass CBAM(nn.Module):def __init__…...
