python实现k_means聚类
K-Means算法是将一组N个样本的特征矩阵X划分为K个无交集的簇,直观上来看是簇是一组一组聚集在一起的数据,在一个簇中的数据就认为是同一类。簇就是聚类的结果表现。
簇中所有数据的均值通常被称为这个簇的“质心”(Centroids)。在一个二维平面中,一簇数据点的质心的横坐标就是这一簇数据点的横坐标的均值,质心的纵坐标就是这一簇数据点的纵坐标的均值。同理可推广至高维空间。
算法实现:
一、随机取n个点,即想要分类数目
二、将当前数据每个点都与取到的n个点进行作差,将差值最小的分为一类
三、将分好类的结果取出计算均值,取出每个类中和均值距离最小的值,将其做为新的中心点
四、重复上述步骤,直到最终分成的簇内结果不再发生变化(在当前的算法里,我们连续验证三次,即在三次内,结果不再发生变化,迭代就会停止)
#k均值计算
import numpy as np
import pandas as pd
import random
import math
def data():
rand_value = [random.randint(1,10000) for i in range(10000)]
# print(rand_value)
# rand_value = [63, 23, 93, 52, 33, 84, 34, 91, 52, 68, 64, 4, 3, 58, 37, 76, 75, 52, 49, 34, 91, 29, 67, 42, 97, 69, 99, 9, 15,
# 44, 12, 46, 86, 92, 10, 67, 46, 93, 49, 29, 93, 95, 60, 33, 30, 63, 24, 45, 26, 47, 12, 62, 50, 54, 13, 62, 40, 39,
# 32, 2, 92, 34, 20, 72, 68, 37, 88, 32, 84, 28, 88, 85, 5, 88, 56, 30, 5, 3, 43, 9, 13, 62, 44, 11, 90, 97, 80, 34,
# 12, 90, 56, 54, 87, 59, 20, 51, 58, 54, 29, 32]
return rand_value
#进行计算,并返回质心及详细信息
def k_mean(data_list,k,rand_choice):
# rand_choice = [random.choice(data_list) for i in range(k)]
temp_dict = {}
for i in range(len(data_list)):
temp_list = []
for j in range(len(rand_choice)):
#解决符号差异带来的影响
temp_list.append(abs(abs(data_list[i]) - abs(rand_choice[j])))
insert_index = temp_list.index(min(temp_list))
if temp_dict.get(rand_choice[insert_index]):
temp_dict[rand_choice[insert_index]].append(data_list[i])
else:
temp_dict[rand_choice[insert_index]] = [data_list[i]]
return temp_dict
#输出距离均值最近的点,返回新的质心及中心点
def min_distince(data_dict):
k_list = []
k_keys = list(data_dict.keys())
for j in range(len(k_keys)):
data_list = data_dict[k_keys[j]]
mean_value = sum(data_list)/len(data_list)
for i in range(len(data_list)):
if i == 0:
distance_value = abs(data_list[i] - mean_value)
s = 0
# distance_list.append(distance_value)
else:
if distance_value > abs(data_list[i] - mean_value):
s = i
distance_value = min(distance_value,abs(data_list[i] - mean_value))
k_list.append(data_list[s])
# distance_list.append(distance_value)
return k_list
def iteration(source_data,k):
iter_num = 0
end_list = []
if len(source_data) < k:
print('需要计算的数据量少于要分类的数据量,请检查数据源\n')
else:
while True:
iter_num += 1
print('迭代次数%d'%iter_num)
if iter_num == 1:
data_dict = k_mean(source_data,k,[random.choice(source_data) for i in range(k)])
end_list.append(data_dict)
# print(data_dict)
result = min_distince(data_dict)
# result = min_distince(k_mean(source_data,k,[random.choice(source_data) for i in range(k)]))
else:
data_dict = k_mean(source_data,k,result)
end_list.append(data_dict)
# print(data_dict)
result = min_distince(data_dict)
if len(end_list) == 4:
del end_list[0]
if end_list[0] == end_list[1] and end_list[1] == end_list[2]:
print(data_dict)
break
if __name__ == '__main__':
source_data = data()
iteration(source_data,5)
相关文章:

python实现k_means聚类
K-Means算法是将一组N个样本的特征矩阵X划分为K个无交集的簇,直观上来看是簇是一组一组聚集在一起的数据,在一个簇中的数据就认为是同一类。簇就是聚类的结果表现。簇中所有数据的均值通常被称为这个簇的“质心”(Centroids)。在一个二维平面中ÿ…...

【批处理脚本】-3.3-exit命令详解
"><--点击返回「批处理BAT从入门到精通」总目录--> 共3页精讲(列举了所有exit的用法,图文并茂,通俗易懂) 在从事“嵌入式软件开发”和“Autosar工具开发软件”过程中,经常会在其集成开发环境IDE(CodeWarrior,S32K DS,Davinci,EB Tresos,ETAS…)中,…...

如果读了我2011年求职前端开发的酸爽经历,希望你可以鼓起勇气继续向前
今年是2023年,如果你觉得今年找工作很难,狗哥回忆了一下2011年求职前端开发工作的酸爽经历,希望你读了以后可以鼓起勇气,不要迷茫,简历投出去石沉大海的,需要改简历的就赶紧改,刷题不到位的就赶…...
)
PTA:L1-016 查验身份证、L1-017 到底有多二、L1-018 大笨钟(C++)
目录 PTA:L1-016 查验身份证 问题描述: 实现代码: L1-017 到底有多二 问题描述: 实现代码: L1-018 大笨钟 问题描述: 实现代码: 都是简单模拟题,不再写题解。 PTA…...

springboot工厂模式解决if_else流程和问题点解决
一、主要问题点 spring中的Bean由IOC容器进行管理,和普通工厂的区别就是springboot中的类不能通过自己New出来使用,如果通过new写入到工厂,涉及到相关实现类调用其他Service(该service在正确情况下正常注入)ÿ…...

如何避免缓存击穿?使用GO语言实现sliglefight
前言 在缓存系统中,如果发生了缓存未命中,通常会向数据库或者其他的缓存系统来请求数据。 想象这样一种情况,缓存系统中某个热点值被删除了,随后一大批请求到来,造成大量的cache miss,如果这些请求全部都…...
【浅学Java】MySQL索引七连炮
MySQL索引面试七连炮0. 谈一下你对索引的理解1. MySQL索引原理和数据结构能介绍一下吗2. B树和B树的区别3. MySQL聚簇索引和非聚簇索引的区别4. 使用MySQL索引都有什么原则4.1 回表4.2 索引覆盖4.3 最左匹配4.4 索引下推5. 不同的存储引擎是如何进行数据的存储的6. MySQL组合索…...

扬帆优配|昔日白马股濒临退市,却6天5涨停!ST股突然集体爆发
尽管再度重申“公司股票将被停止上市”,但3月8日早间,*ST辅仁股价仍是在开盘后快速封住涨停板。这已是该公司近6个买卖日来,第5次呈现涨停。 无独有偶,8日早间ST东瀛也在此前多次涨停后,再度呈现近4%的涨幅。而就在7日…...

Git 基础(一)—— Git 的安装及其配置
目录 一、Git 的下载与安装 1、Linux 环境 2、Windows 环境 (1) 下载 Git 安装包 (2) 安装 Git 二、Git 配置 1、配置用户信息 2、查看配置信息 3、Windows 环境下配置文件的位置 一、Git 的下载与安装 1、Linux 环境 在保证网络环境畅通的情况下,直接输…...

什么是信息安全风险评估?企业如何做?
什么是信息安全风险评估? 信息安全风险评估是参照风险评估标准和管理规范,对信息系统的资产价值、潜在威胁、薄弱环节、已采取的防护措施等进行分析,判断安全事件发生的概率以及可能造成的损失,提出风险管理措施的过程。当风险评…...
HBase---idea操作Hbase数据库并且映射到Hive
idea操作Hbase数据库并且映射到Hive 文章目录idea操作Hbase数据库并且映射到Hiveidea操作Hbase数据库环境准备启动服务创建Maven工程在测试类中编写初始化方法在测试类中编写关闭方法在测试类中编写创建命名空间方法在测试类中编写创建表方法在测试类中编写查看表结构方法在测试…...
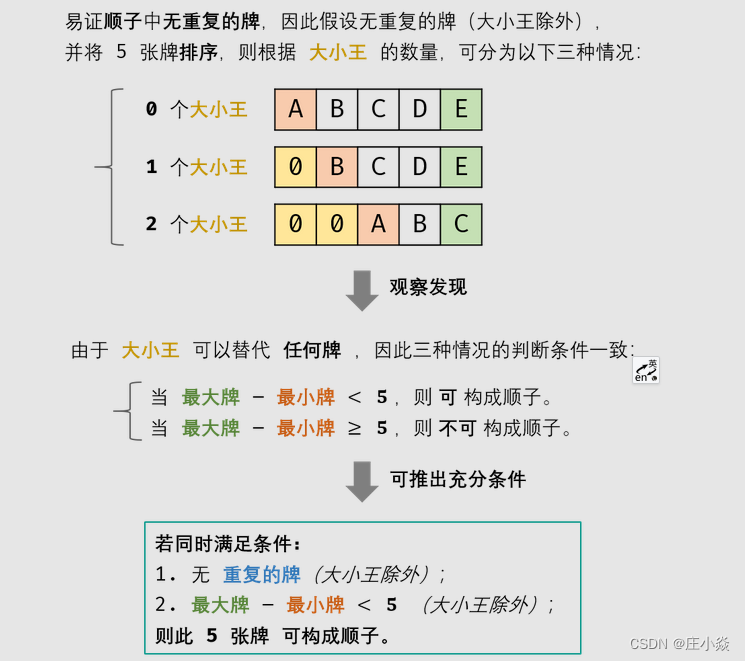
剑指 Offer 61 扑克牌中的顺子
摘要 扑克牌中的顺子 一、集合 Set 遍历 根据题意,此5张牌是顺子的 充分条件 如下: 除大小王外,所有牌 无重复 ;设此5张牌中最大的牌为max,最小的牌为min(大小王除外),则需满足…...
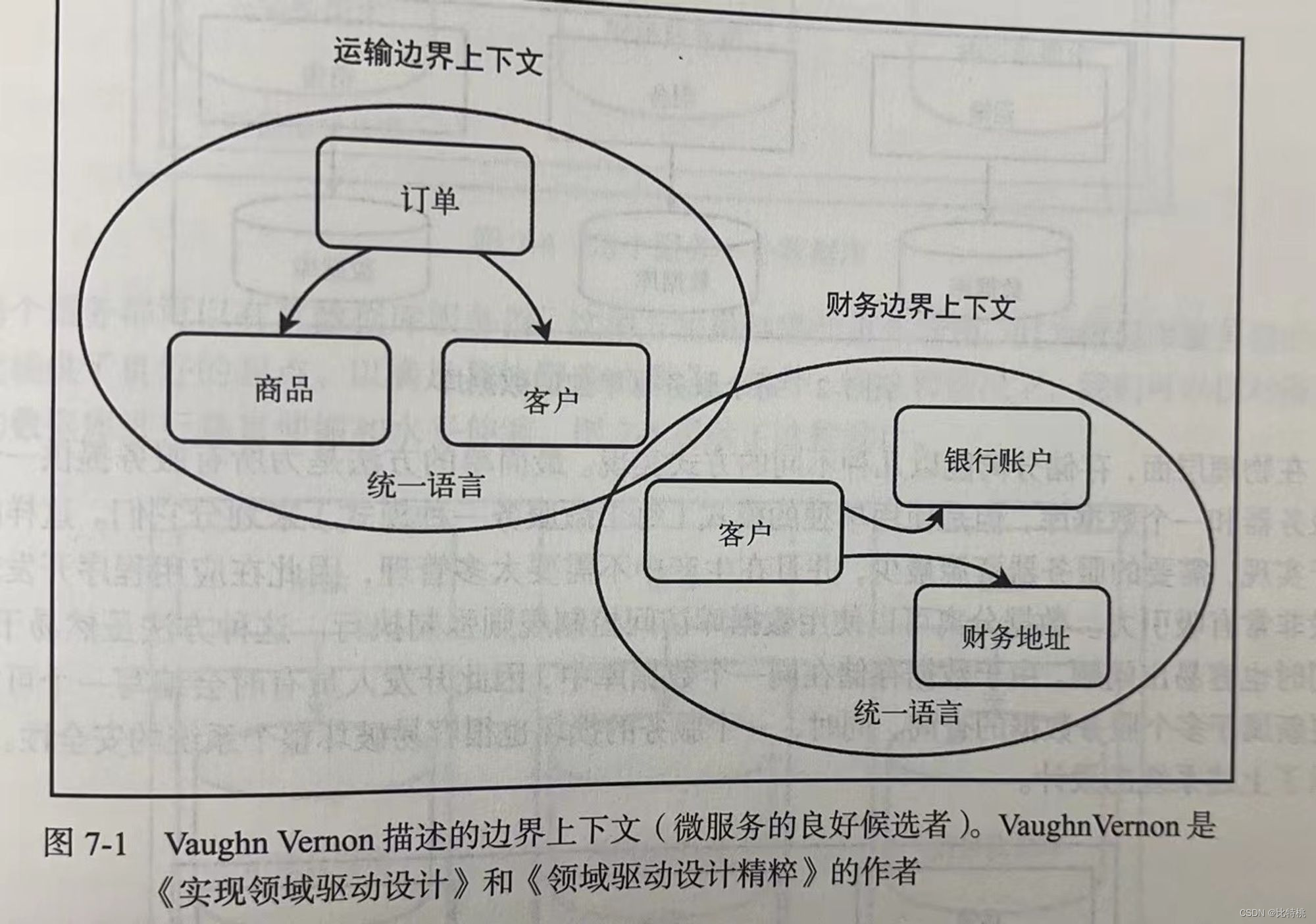
Spring 响应式编程-读书笔记
序言 大家好,我是比特桃。本文为《Spring 响应式编程》的读书笔记,响应式技术栈可以创建极其高效、易于获取且具有回弹性的端点,同时响应式可以容忍网络延迟,并以影响较小的方式处理故障。响应式微服务还可以隔离慢速事务并加速速…...
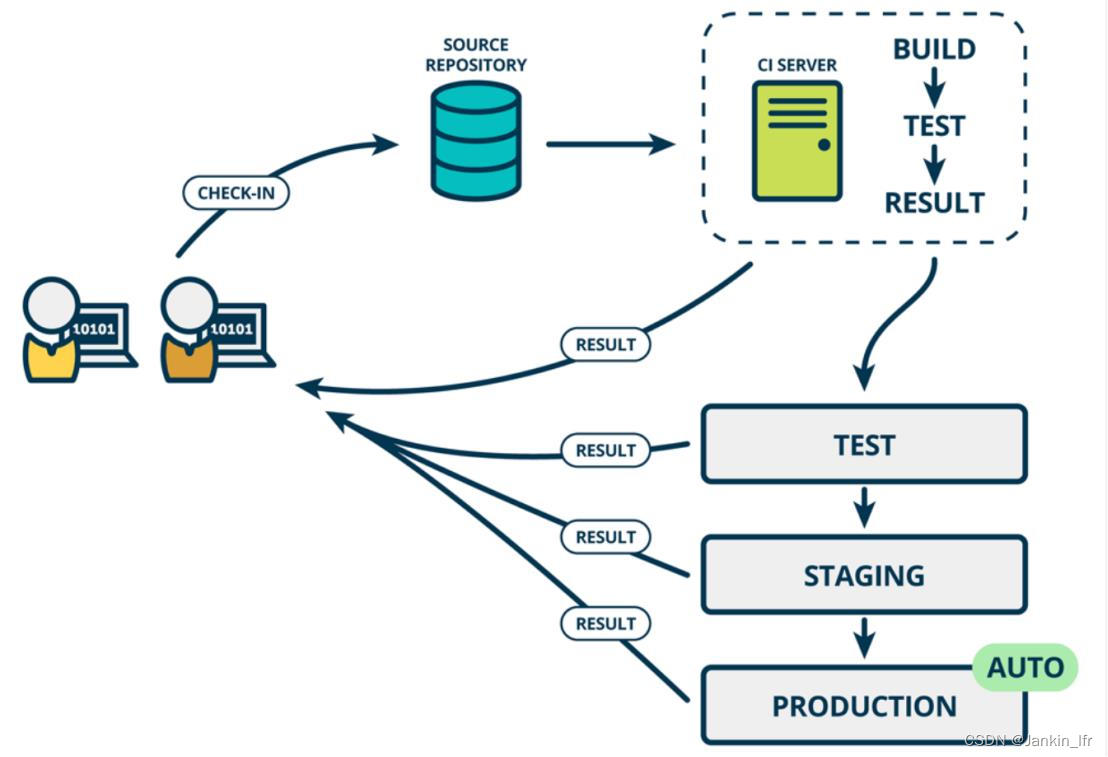
CI流水线的理解
一、概念 单元测试:针对软件的基本单元(如:类、函数)所做的测试。 集成测试:将软件代码单元集成起来后,以组件、模块和子系统为单位进行的测试,主要测试接口间的交互关系。也称组件测试…...
OpenStack手动分布式部署Nova【Queens版】
目录 Nove简介: 1、登录数据库配置(在controller执行) 1.1登录数据库 1.2数据库里创建nova-api 1.3数据库登录授权 1.4创建nova用户 1.5添加admin用户为nova用户 1.6创建nova服务端点 1.7创建compute API 服务端点 1.8创建一个placement服务…...

centos7 oracle19c安装 ORA-01012: not logged on
总共分三步 1.下载安装包:里面有一份详细的安装教程 链接:https://pan.baidu.com/s/1Of2a72pNLZ-DDIWKrTQfLw?pwd8NAx 提取码:8NAx 2.安装后,执行初始化:时间较长 /etc/init.d/oracledb_ORCLCDB-19c configure 3.配置环境变量,不配置环境变量,sq…...

山东小巨人申报条件
国家专精特新小巨人特点1、经济效益:上年度企业营业收入在1亿元至4亿元之间,近2年主营业务收入或净利润的平均增长率达到10%以上,企业资产负债率不高于70%。2、专业化程度:(1)企业从事特定细分市场时间达到…...

手写中实现并学习ahooks——useRequest
前言 最近业务没有之前紧张了,也是消失了一段时间,也总结了一些之前业务上的问题。 和同事沟通也是发现普通的async await 封装api在复杂业务场景下针对于请求的业务逻辑比较多,也是推荐我去学习一波ahooks,由于问题起源于请求…...

[手写OS]动手实现一个OS 之 准备工作以及引导扇区
[手写OS]动手实现一个OS之第一步-环境以及引导扇区 环境准备 一台可用计算机(linux我不知道,我用的Windows)汇编编译器NASM一个方便的软盘读写工具VirtualBox 汇编编译器NASM 官网地址:https://www.nasm.us/pub/nasm/snapshot…...

JVM实战OutOfMemoryError异常
目录 Java堆溢出 常见原因: 虚拟机栈和本地方法栈溢出 实验1:虚拟机栈和本地方法栈测试(作为第1点测试程序) 实验2:(作为第1点测试程序) 运行时常量池和方法区溢出 运行时常量池内存溢出 …...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...
