【深度探讨】公共部门在选择区块链平台时要考虑的6个方面

发表时间:2022年8月17日
信息来源:bsvblockchain.org
与私营企业相比,全球的公共部门组织在考虑升级软件解决方案时面临着一系列的全新挑战。公共部门的决策流程冗长而复杂,他们要不惜一切代价避免对现有业务造成干扰,最重要的是,公共部门必须向公众证明,花费这些成本的目的是为大众服务。但如果被摆上台面的是一种区块链解决方案,那么尽职调查的过程往往会更加漫长且复杂。
公共部门的决策方法论
公共部门的方法论与私营部门不同,因为如果要实施像BSV区块链这样的新型软件平台,所有的公共支出都必须被证明是合理的。
仅仅因为一种产品似乎非常适合某一企业(或任意企业),也并不意味着同样的解决方案就适合公共部门。引入区块链技术等新型解决方案需要有一个令人信服的商业案例,并且解决方案需要适合这项业务。
商业案例的合理性必须得到证明,要确定优先事项并进行权衡,以确保初始项目对现有用户体验的影响最小,并且那些会影响组织日常运作的变动不能对性能产生影响。
在公共部门组织中实施复杂的解决方案是一项庞大的任务,往往涉及整个部门,且需要耗时多年。这不是一项信手拈来的任务。
在对基础设施进行改动之前需要考虑的6个要素
当发起人和决策者团队坐在一起考虑一个新平台时,在将现有的数据库解决方案更改为区块链平台之前,应该考虑以下几个方面。
1.物有所值
要提供物有所值的最佳性价比解决方案。引入区块链后,能否通过其技术优势和相关活动为社会带来最大的社会价值?
2.商业可行性
所选择的解决方案必须能够满足客户的各种需求,并在各个商业领域进行交付。它必须考虑到关键的成功因素,并且所选的入围方案都应该可以实现最后交付。
3.即时可用
任何解决方案都必须符合可及性的要求,以便网站或应用能够被尽可能多的人使用。它必须是非歧视性的,不得以任何方式进行歧视。任何决策都应该关注由数据驱动且稳定的解决方案,并满足决策者对性能、速度、效率和成本节约的要求。
4.成功交付
通过可扩容且交易费用较低的现成区块链,公共部门组织能够使用有效的现有技术,而无需面临协议变动或修改的情况。
5.战略价值
区块链解决方案必须与公共部门的短期和长期规划目标相匹配,并通过提供转型变革的需求来解决客户的痛点。这一解决方案必须支持国家和地方的政策、目标和指标。
6.解决方案的后续管理
区块链必须能够符合组织要求,以便在交付后对平台进行监测、管理和评估。任何设计问题都应被细致考虑,并制定相应的应急计划,从而可根据最初的用户测试来对解决方案进行调整。
在公共项目中实施区块链方案
在公共部门组织中,确定哪些基础设施领域适合使用区块链解决方案是一项复杂的任务。公共部门的项目往往是严重孤立的,而区块链解决方案则可以解决公共部门各部门间的一系列问题。通常而言,一个团队可通过一系列的功能来对潜在机会进行评估,从而得到一个组合的视角。这需要大量的时间和跨团队协调,并需要落实一个矩阵管理组织。
然而,实施一种新型的解决方案也是有风险的。如果没有充分的规划,所有的项目都有失败的风险。幸运的是,BSV区块链已经正常运行了很多年,不容易因为开发者或管理人员的心血来潮就改动协议或更新代码。
其稳定性使得它对那些希望实施长期解决方案的部门具有吸引力,而这些部门也希望解决方案不会因成本过高或服务变更而被修改、废弃或取消。在考虑新的解决方案是否能够满足或超越项目的服务级别协议(SLA)要求并有效优化现有解决方案时,这种稳定性正是着眼于大局的团队所欣赏的。
BSV区块链如何对公共部门进行超级充能
BSV区块链具备无限容量,既能满足当前的业务需求,又能为未来任意时间的任何计划或设想之中的用量爆发场景提供足够的空间。对于实施团队来说,最大的挑战则是:如何说服众多的政府部门相信这一解决方案将超越他们的预期。
目前,全球已有超过400个项目构建于BSV区块链之上。凭借坚如磐石的协议及超高的网络性能,BSV生态系统迅猛发展,我们期待未来出现更多前所未有的商业应用。
- 对BSV区块链开发感兴趣的朋友,可以前往我们的中文开发者专区:BSV区块链
相关文章:

【深度探讨】公共部门在选择区块链平台时要考虑的6个方面
发表时间:2022年8月17日 信息来源:bsvblockchain.org 与私营企业相比,全球的公共部门组织在考虑升级软件解决方案时面临着一系列的全新挑战。公共部门的决策流程冗长而复杂,他们要不惜一切代价避免对现有业务造成干扰,…...
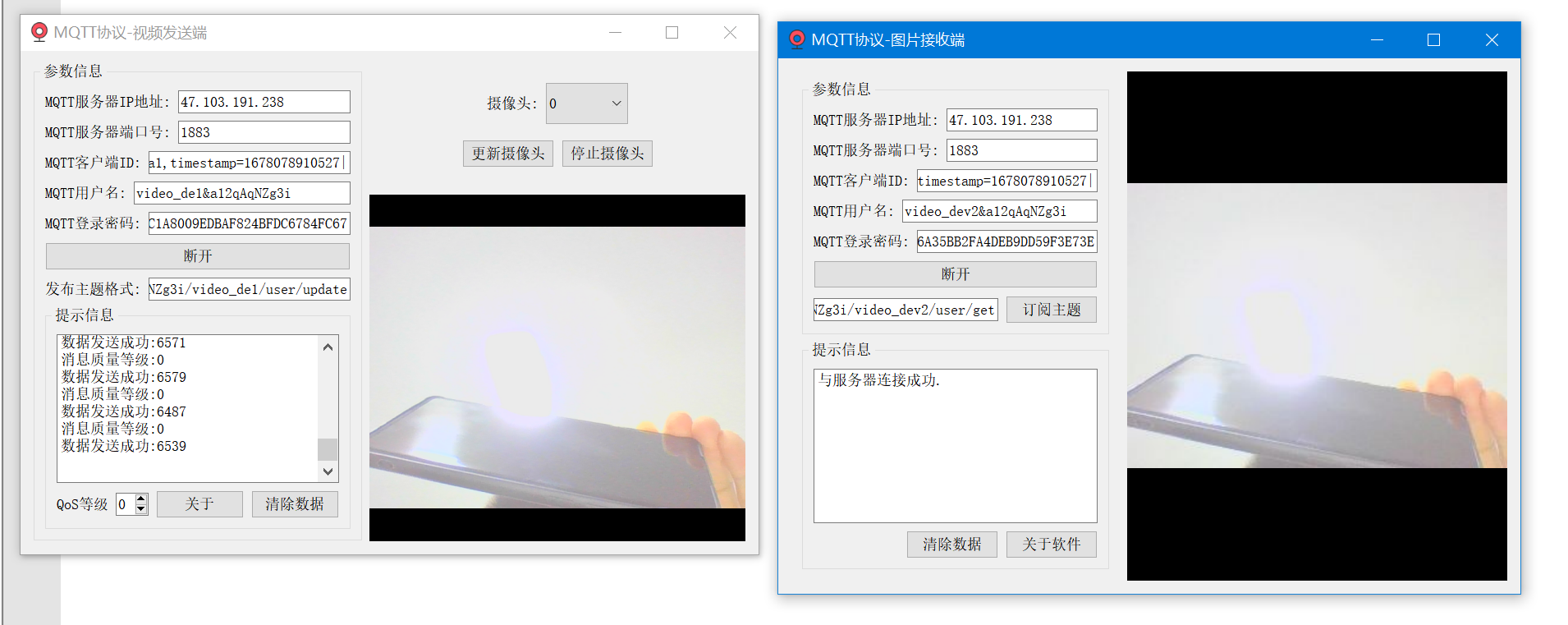
基于阿里云物联网平台设计的实时图传系统_采用MQTT协议传输图像
一、项目功能介绍 当前基于MQTT协议设计了一个实时图传系统,通过这个项目来演示,两个MQTT设备如何互相订阅,进行消息流转。 在阿里云服务器上创建2个设备,分为为设备A和设备B;设备A负责采集本地摄像头画面上传,设备B负责接收设备A上传的数据然后解析显示出来。在阿里云服…...
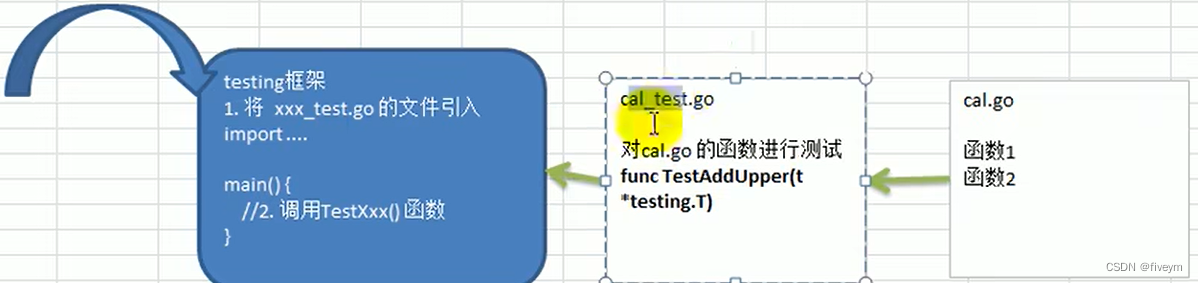
42-Golang中的单元测试
Golang中的单元测试需求传统方法基本介绍单元测试快速入门总结综合案例需求 在工作中,我们会遇到这样的情况,就是去确认一个函数,或者一个模块的结果是否正确 传统方法 在main函数中,调用addUpper函数,看看实际输出…...

python实现k_means聚类
K-Means算法是将一组N个样本的特征矩阵X划分为K个无交集的簇,直观上来看是簇是一组一组聚集在一起的数据,在一个簇中的数据就认为是同一类。簇就是聚类的结果表现。簇中所有数据的均值通常被称为这个簇的“质心”(Centroids)。在一个二维平面中ÿ…...

【批处理脚本】-3.3-exit命令详解
"><--点击返回「批处理BAT从入门到精通」总目录--> 共3页精讲(列举了所有exit的用法,图文并茂,通俗易懂) 在从事“嵌入式软件开发”和“Autosar工具开发软件”过程中,经常会在其集成开发环境IDE(CodeWarrior,S32K DS,Davinci,EB Tresos,ETAS…)中,…...

如果读了我2011年求职前端开发的酸爽经历,希望你可以鼓起勇气继续向前
今年是2023年,如果你觉得今年找工作很难,狗哥回忆了一下2011年求职前端开发工作的酸爽经历,希望你读了以后可以鼓起勇气,不要迷茫,简历投出去石沉大海的,需要改简历的就赶紧改,刷题不到位的就赶…...
)
PTA:L1-016 查验身份证、L1-017 到底有多二、L1-018 大笨钟(C++)
目录 PTA:L1-016 查验身份证 问题描述: 实现代码: L1-017 到底有多二 问题描述: 实现代码: L1-018 大笨钟 问题描述: 实现代码: 都是简单模拟题,不再写题解。 PTA…...

springboot工厂模式解决if_else流程和问题点解决
一、主要问题点 spring中的Bean由IOC容器进行管理,和普通工厂的区别就是springboot中的类不能通过自己New出来使用,如果通过new写入到工厂,涉及到相关实现类调用其他Service(该service在正确情况下正常注入)ÿ…...

如何避免缓存击穿?使用GO语言实现sliglefight
前言 在缓存系统中,如果发生了缓存未命中,通常会向数据库或者其他的缓存系统来请求数据。 想象这样一种情况,缓存系统中某个热点值被删除了,随后一大批请求到来,造成大量的cache miss,如果这些请求全部都…...
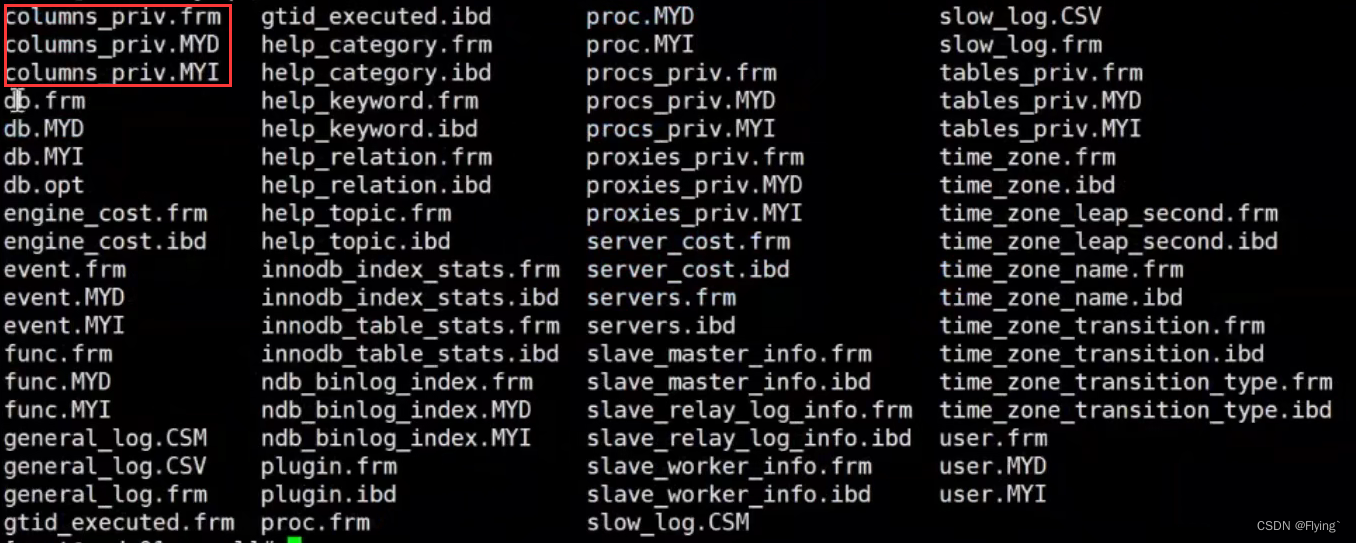
【浅学Java】MySQL索引七连炮
MySQL索引面试七连炮0. 谈一下你对索引的理解1. MySQL索引原理和数据结构能介绍一下吗2. B树和B树的区别3. MySQL聚簇索引和非聚簇索引的区别4. 使用MySQL索引都有什么原则4.1 回表4.2 索引覆盖4.3 最左匹配4.4 索引下推5. 不同的存储引擎是如何进行数据的存储的6. MySQL组合索…...

扬帆优配|昔日白马股濒临退市,却6天5涨停!ST股突然集体爆发
尽管再度重申“公司股票将被停止上市”,但3月8日早间,*ST辅仁股价仍是在开盘后快速封住涨停板。这已是该公司近6个买卖日来,第5次呈现涨停。 无独有偶,8日早间ST东瀛也在此前多次涨停后,再度呈现近4%的涨幅。而就在7日…...

Git 基础(一)—— Git 的安装及其配置
目录 一、Git 的下载与安装 1、Linux 环境 2、Windows 环境 (1) 下载 Git 安装包 (2) 安装 Git 二、Git 配置 1、配置用户信息 2、查看配置信息 3、Windows 环境下配置文件的位置 一、Git 的下载与安装 1、Linux 环境 在保证网络环境畅通的情况下,直接输…...

什么是信息安全风险评估?企业如何做?
什么是信息安全风险评估? 信息安全风险评估是参照风险评估标准和管理规范,对信息系统的资产价值、潜在威胁、薄弱环节、已采取的防护措施等进行分析,判断安全事件发生的概率以及可能造成的损失,提出风险管理措施的过程。当风险评…...
HBase---idea操作Hbase数据库并且映射到Hive
idea操作Hbase数据库并且映射到Hive 文章目录idea操作Hbase数据库并且映射到Hiveidea操作Hbase数据库环境准备启动服务创建Maven工程在测试类中编写初始化方法在测试类中编写关闭方法在测试类中编写创建命名空间方法在测试类中编写创建表方法在测试类中编写查看表结构方法在测试…...
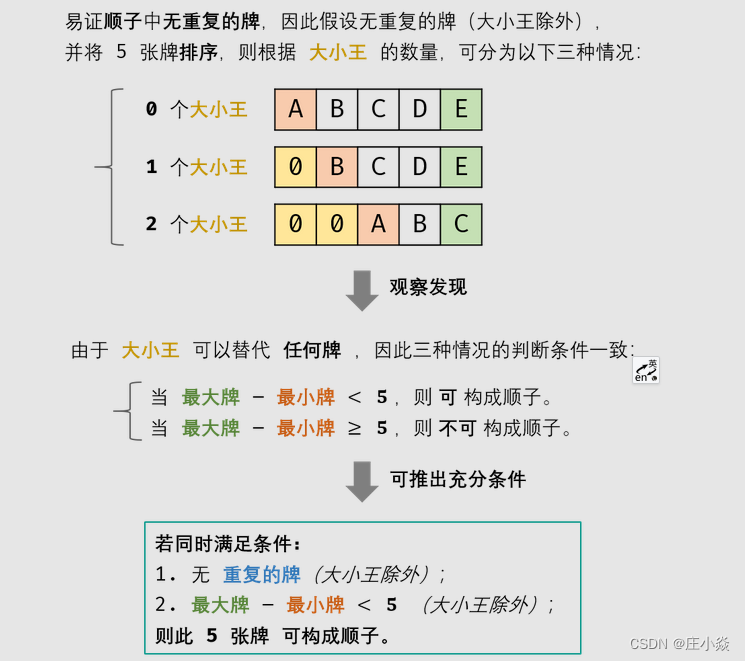
剑指 Offer 61 扑克牌中的顺子
摘要 扑克牌中的顺子 一、集合 Set 遍历 根据题意,此5张牌是顺子的 充分条件 如下: 除大小王外,所有牌 无重复 ;设此5张牌中最大的牌为max,最小的牌为min(大小王除外),则需满足…...
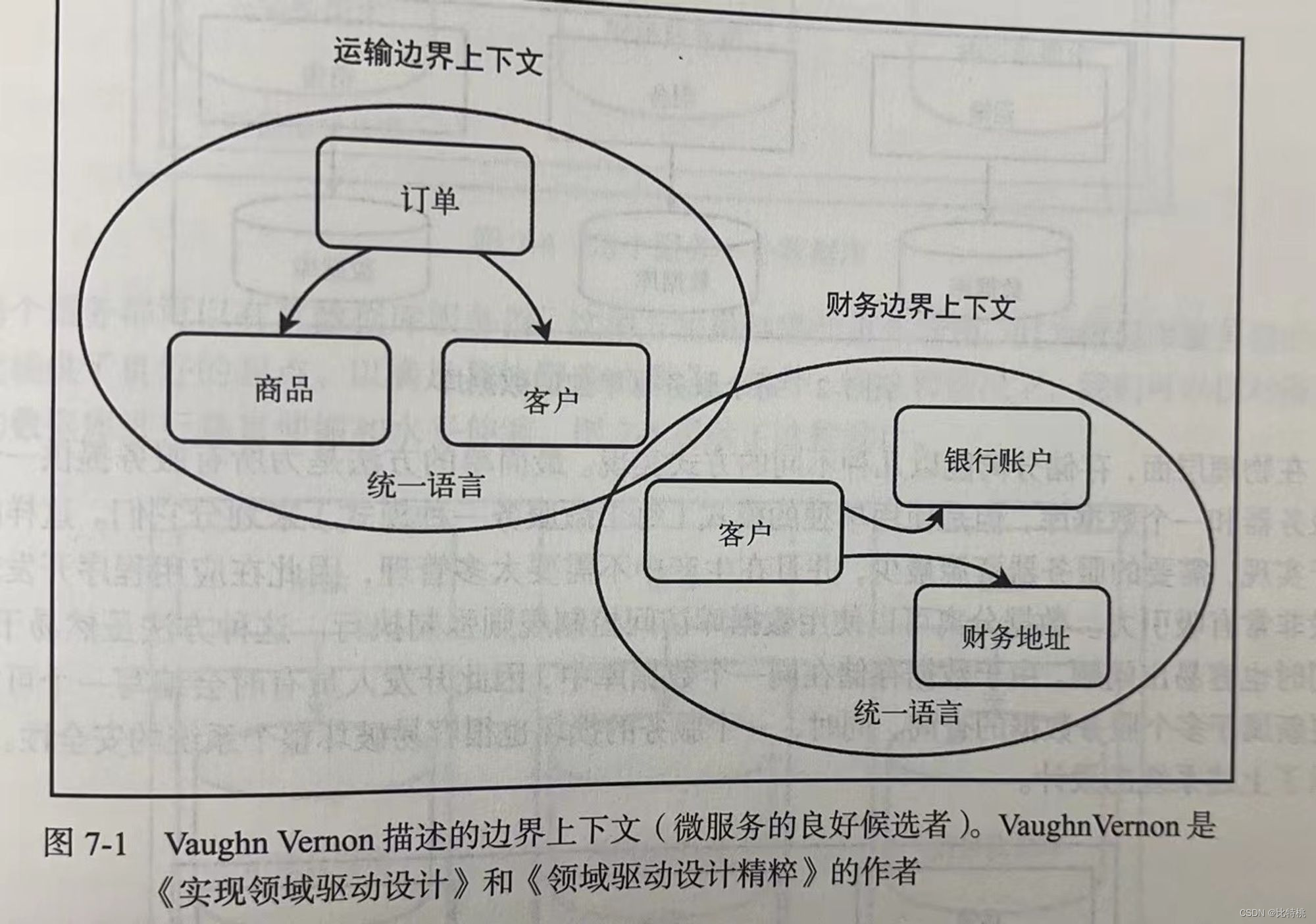
Spring 响应式编程-读书笔记
序言 大家好,我是比特桃。本文为《Spring 响应式编程》的读书笔记,响应式技术栈可以创建极其高效、易于获取且具有回弹性的端点,同时响应式可以容忍网络延迟,并以影响较小的方式处理故障。响应式微服务还可以隔离慢速事务并加速速…...
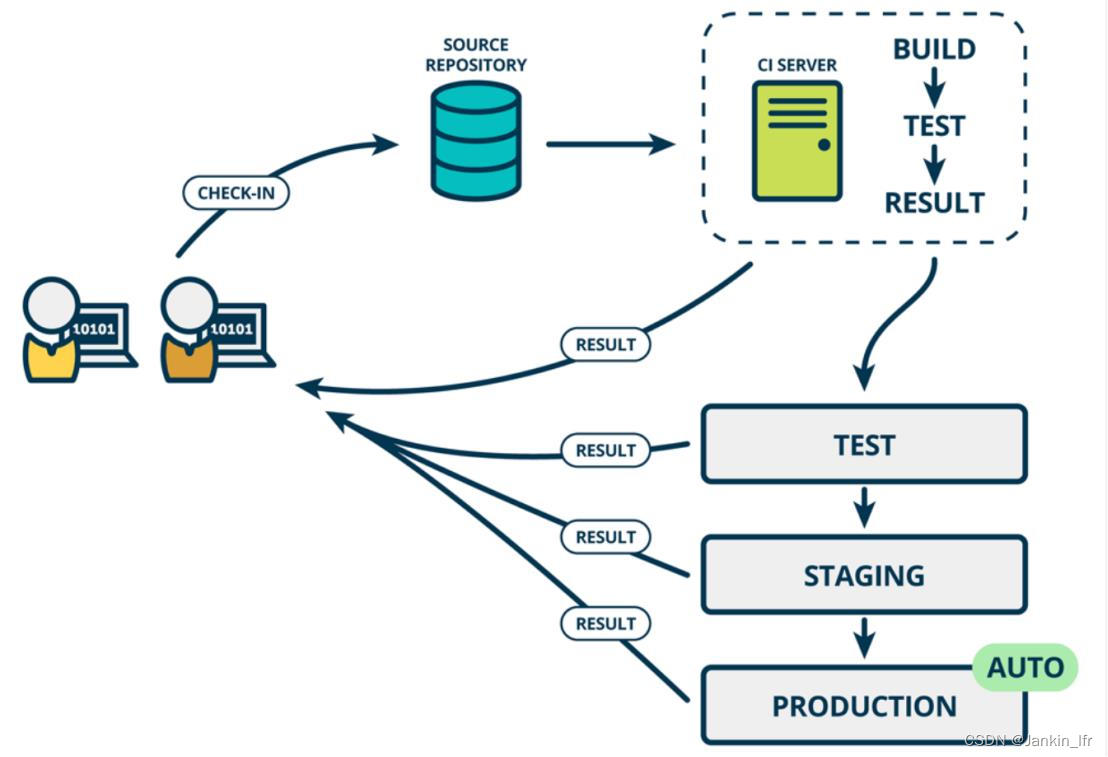
CI流水线的理解
一、概念 单元测试:针对软件的基本单元(如:类、函数)所做的测试。 集成测试:将软件代码单元集成起来后,以组件、模块和子系统为单位进行的测试,主要测试接口间的交互关系。也称组件测试…...
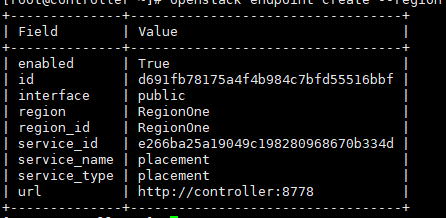
OpenStack手动分布式部署Nova【Queens版】
目录 Nove简介: 1、登录数据库配置(在controller执行) 1.1登录数据库 1.2数据库里创建nova-api 1.3数据库登录授权 1.4创建nova用户 1.5添加admin用户为nova用户 1.6创建nova服务端点 1.7创建compute API 服务端点 1.8创建一个placement服务…...

centos7 oracle19c安装 ORA-01012: not logged on
总共分三步 1.下载安装包:里面有一份详细的安装教程 链接:https://pan.baidu.com/s/1Of2a72pNLZ-DDIWKrTQfLw?pwd8NAx 提取码:8NAx 2.安装后,执行初始化:时间较长 /etc/init.d/oracledb_ORCLCDB-19c configure 3.配置环境变量,不配置环境变量,sq…...

山东小巨人申报条件
国家专精特新小巨人特点1、经济效益:上年度企业营业收入在1亿元至4亿元之间,近2年主营业务收入或净利润的平均增长率达到10%以上,企业资产负债率不高于70%。2、专业化程度:(1)企业从事特定细分市场时间达到…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

goreplay
1.github地址 https://github.com/buger/goreplay 2.简单介绍 GoReplay 是一个开源的网络监控工具,可以记录用户的实时流量并将其用于镜像、负载测试、监控和详细分析。 3.出现背景 随着应用程序的增长,测试它所需的工作量也会呈指数级增长。GoRepl…...
