Apache Seata基于改良版雪花算法的分布式UUID生成器分析2
title: 关于新版雪花算法的答疑
author: selfishlover
keywords: [Seata, snowflake, UUID, page split]
date: 2021/06/21
本文来自 Apache Seata官方文档,欢迎访问官网,查看更多深度文章。
关于新版雪花算法的答疑
在上一篇关于新版雪花算法的解析中,我们提到新版算法所做出的2点改变:
- 时间戳不再时刻追随系统时钟。
- 节点ID和时间戳互换位置。由原版的:

改成:
有细心的同学提出了一个问题:新版算法在单节点内部确实是单调递增的,但是在多实例部署时,它就不再是全局单调递增了啊!因为显而易见,节点ID排在高位,那么节点ID大的,生成的ID一定大于节点ID小的,不管时间上谁先谁后。而原版算法,时间戳在高位,并且始终追随系统时钟,可以保证早生成的ID小于晚生成的ID,只有当2个节点恰好在同一时间戳生成ID时,2个ID的大小才由节点ID决定。这样看来,新版算法是不是错的?
这是一个很好的问题!能提出这个问题的同学,说明已经深入思考了标准版雪花算法和新版雪花算法的本质区别,这点值得鼓励!在这里,我们先说结论:新版算法的确不具备全局的单调递增性,但这不影响我们的初衷(减少数据库的页分裂)。这个结论看起来有点违反直觉,但可以被证明。
在证明之前,我们先简单回顾一下数据库关于页分裂的知识。以经典的mysql innodb为例,innodb使用B+树索引,其中,主键索引的叶子节点还保存了数据行的完整记录,叶子节点之间以双向链表的形式串联起来。叶子节点的物理存储形式为数据页,一个数据页内最多可以存储N条行记录(N与行的大小成反比)。如图所示:
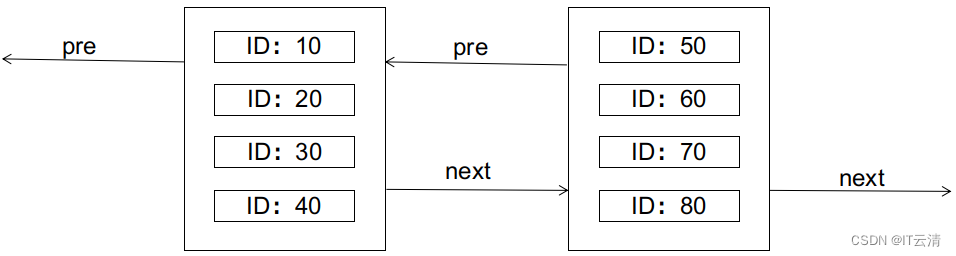
B+树的特性要求,左边的节点应小于右边的节点。如果此时要插入一条ID为25的记录,会怎样呢(假设每个数据页只够存放4条记录)?答案是会引起页分裂,如图:
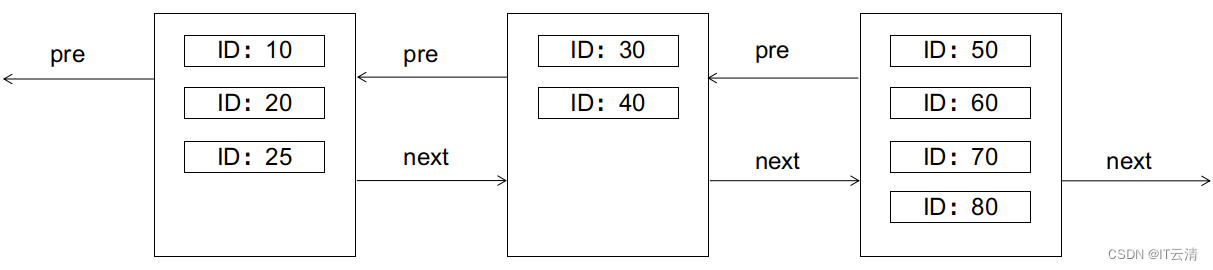
页分裂是IO不友好的,需要新建数据页,拷贝转移旧数据页的部分记录等,我们应尽量避免。
理想的情况下,主键ID最好是顺序递增的(例如把主键设置为auto_increment),这样就只会在当前数据页放满了的时候,才需要新建下一页,双向链表永远是顺序尾部增长的,不会有中间的节点发生分裂的情况。
最糟糕的情况下,主键ID是随机无序生成的(例如java中一个UUID字符串),这种情况下,新插入的记录会随机分配到任何一个数据页,如果该页已满,就会触发页分裂。
如果主键ID由标准版雪花算法生成,最好的情况下,是每个时间戳内只有一个节点在生成ID,这时候算法的效果等同于理想情况的顺序递增,即跟auto_increment无差。最坏的情况下,是每个时间戳内所有节点都在生成ID,这时候算法的效果接近于无序(但仍比UUID的完全无序要好得多,因为workerId只有10位决定了最多只有1024个节点)。实际生产中,算法的效果取决于业务流量,并发度越低,算法越接近理想情况。
那么,换成新版算法又会如何呢?
新版算法从全局角度来看,ID是无序的,但对于每一个workerId,它生成的ID都是严格单调递增的,又因为workerId是有限的,所以最多可划分出1024个子序列,每个子序列都是单调递增的。
对于数据库而言,也许它初期接收的ID都是无序的,来自各个子序列的ID都混在一起,就像这样:
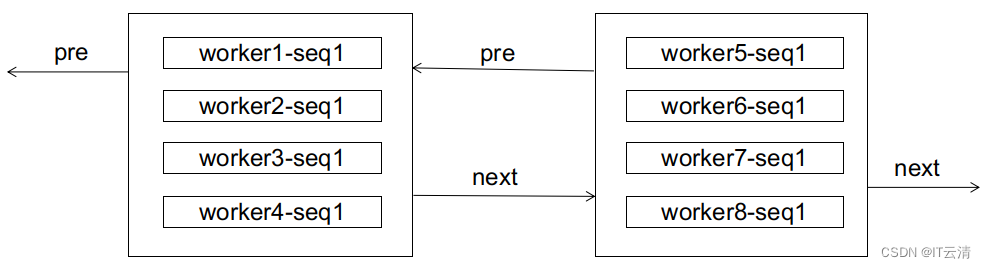
如果这时候来了个worker1-seq2,显然会造成页分裂:

但分裂之后,有趣的事情发生了,对于worker1而言,后续的seq3,seq4不会再造成页分裂(因为还装得下),seq5也只需要像顺序增长那样新建页进行链接(区别是这个新页不是在双向链表的尾部)。注意,worker1的后续ID,不会排到worker2及之后的任意节点(因而不会造成后边节点的页分裂),因为它们总比worker2的ID小;也不会排到worker1当前节点的前边(因而不会造成前边节点的页分裂),因为worker1的子序列总是单调递增的。在这里,我们称worker1这样的子序列达到了稳态,意为这条子序列已经"稳定"了,它的后续增长只会出现在子序列的尾部,而不会造成其它节点的页分裂。
同样的事情,可以推广到各个子序列上。无论前期数据库接收到的ID有多乱,经过有限次的页分裂后,双向链表总能达到这样一个稳定的终态:
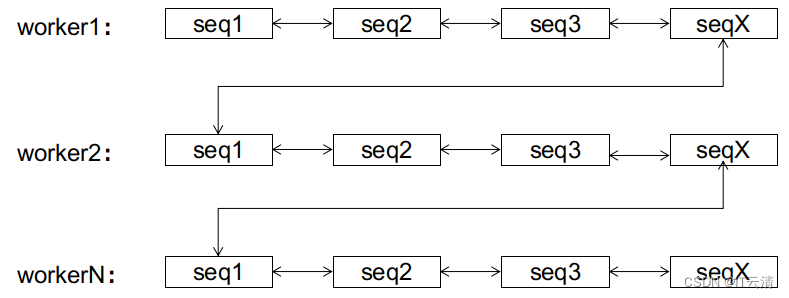
到达终态后,后续的ID只会在该ID所属的子序列上进行顺序增长,而不会造成页分裂。该状态下的顺序增长与auto_increment的顺序增长的区别是,前者有1024个增长位点(各个子序列的尾部),后者只有尾部一个。
到这里,我们可以回答开头所提出的问题了:新算法从全局来看的确不是全局递增的,但该算法是收敛的,达到稳态后,新算法同样能达成像全局顺序递增一样的效果。
扩展思考
以上只提到了序列不停增长的情况,而实践生产中,不光有新数据的插入,也有旧数据的删除。而数据的删除有可能会导致页合并(innodb若发现相邻2个数据页的空间利用率都不到50%,就会把它俩合并),这对新算法的影响如何呢?
经过上面的流程,我们可以发现,新算法的本质是利用前期的页分裂,把不同的子序列逐渐分离开来,让算法不断收敛到稳态。而页合并则恰好相反,它有可能会把不同的子序列又合并回同一个数据页里,妨碍算法的收敛。尤其是在收敛的前期,频繁的页合并甚至可以让算法永远无法收敛(你刚分离出来我就又把它们合并回去,一夜回到解放前~)!但在收敛之后,只有在各个子序列的尾节点进行的页合并,才有可能破坏稳态(一个子序列的尾节点和下一个子序列的头节点进行合并)。而在子序列其余节点上的页合并,不影响稳态,因为子序列仍然是有序的,只不过长度变短了而已。
以seata的服务端为例,服务端那3张表的数据的生命周期都是比较短的,一个全局事务结束之后,它们就会被清除了,这对于新算法是不友好的,没有给时间它进行收敛。不过已经有延迟删除的PR在review中,搭配这个PR,效果会好很多。比如定期每周清理一次,前期就有足够的时间给算法进行收敛,其余的大部分时间,数据库就能从中受益了。到期清理时,最坏的结果也不过是表被清空,算法从头再来。
如果您希望把新算法应用到业务系统当中,请务必确保算法有时间进行收敛。比如用户表之类的,数据本就打算长期保存的,算法可以自然收敛。或者也做了延迟删除的机制,给算法足够的时间进行收敛。
如果您有更好的意见和建议,也欢迎跟seata社区联系!
相关文章:

Apache Seata基于改良版雪花算法的分布式UUID生成器分析2
title: 关于新版雪花算法的答疑 author: selfishlover keywords: [Seata, snowflake, UUID, page split] date: 2021/06/21 本文来自 Apache Seata官方文档,欢迎访问官网,查看更多深度文章。 关于新版雪花算法的答疑 在上一篇关于新版雪花算法的解析中…...

13、揭秘JVM垃圾回收器:面试必备知识,你掌握了吗?
13.1、前文回顾 在上一篇文章中,我们详细分析了触发Minor GC的时机,以及对象何时会从新生代迁移到老年代。我们还讨论了为了确保新生代向老年代的内存迁移安全,需要在Minor GC之前如何检查老年代的内存空间,以及在什么情况下会触发老年代的Full GC,以及老年代的垃圾回收算…...
治疗耳鸣患者案例分享第二期
“患者耳鸣20年了,目前耳朵没有堵或者胀的感觉,但是偶尔有点痒,平时会有头晕头胀这种情况,然后头晕是稍微晕炫一下。然后头疼是经常有的,头胀不经常。” 患者耳鸣持续20年,虽然耳朵没有堵或胀的感觉&#x…...

数据加密的方法
这些方法可以单独或结合使用,以提高数据的安全性和保护隐私。 对称加密:使用相同的密钥对数据进行加密和解密。常见的对称加密算法包括DES、AES和RC4。 非对称加密:使用一对密钥(公钥和私钥)对数据进行加密和解密。发…...

Android BINDER是干嘛的?
1.系统架构 2.binder 源码位置: 与LINUX传统IPC对比...
)
运维各种中间件的手动安装(非常详细)
压缩文件夹 tar -zcvf newFolder.tar.gz oldFolder 把oldFolder文件夹压缩成newFolder.tar.gz解压文件夹 tar -zxvf 压缩文件名.tar.gzlinux安装jdk (参考 https://blog.csdn.net/qq_42269466/article/details/124079963 ) 1、创建目录存放jdk包 mkd…...

【Android】Android应用性能优化总结
AndroidApp应用性能优化总结 最近大半年的时间里,大部分投在了某国内新能源汽车的某款AndroidApp开发上。 由于该App是该款车上,常用重点应用。所以车厂对应用性能的要求比较高。 主要包括: 应用冷启动达到***ms。应用热(温)启动达到***ms应…...

FBA头程海运发货流程是怎样的?
FBA头程发货作为整个FBA流程的关键一环,更是直接影响到商品从起点到终点的流通效率和成本。其中,海运作为一种经济、稳定的运输方式,在FBA头程发货中扮演着举足轻重的角色。那么,FBA头程海运发货流程究竟是怎样的呢? 1、装箱与发…...
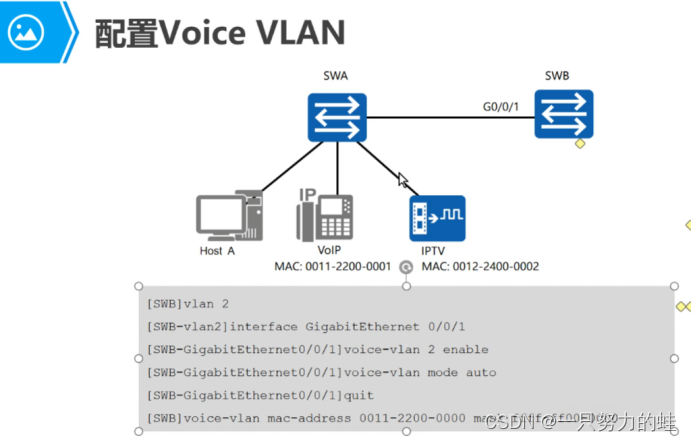
二、VLAN原理和配置
vlan不是协议,是一个技术,虚拟局域网技术,基于802.1q协议。 vlan(虚拟局域网),将一个物理的局域网在逻辑上划分成多个广播域的技术。 目录 1.冲突域和广播域 概念 范围 2.以太网帧格式 3.以太网帧封装…...
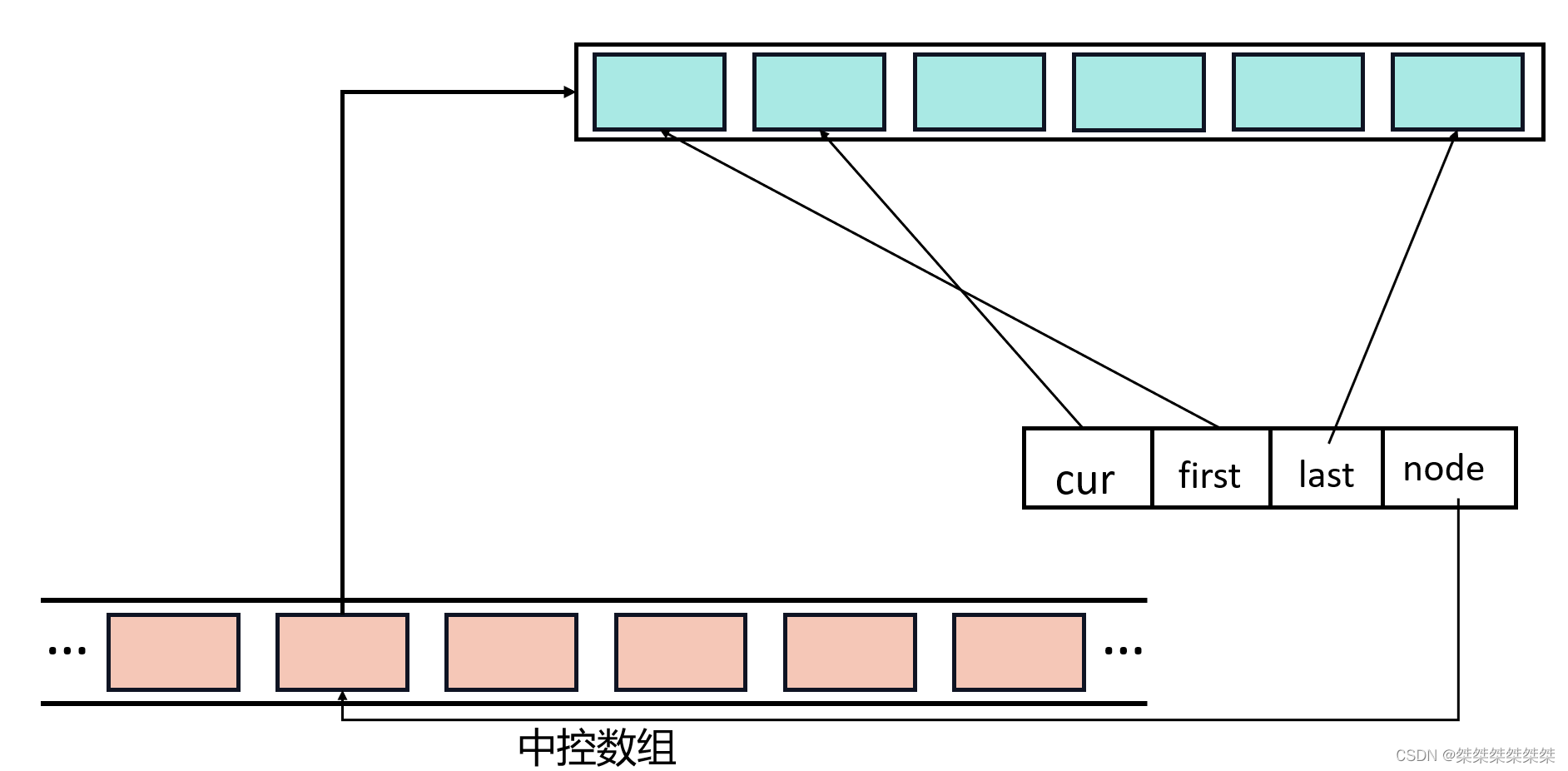
stackqueue类——适配器模式 双端队列deque(C++)
接下来我们将实现 stack、queue 类的常用函数,其实对于 stack 和 queue 的常用函数实现可以说得上是非常简单,若想详细了解可以看这篇:栈和队列&循环队列(C/C)_栈和循环队列-CSDN博客;在本篇中我们将使…...

SpringCloud知识点梳理
1. Spring Cloud 综述 1.1 Spring Cloud 是什么 [百度百科]Spring Cloud是⼀系列框架的有序集合。它利⽤Spring Boot的开发便利性巧妙地简化了分布式系统基础设施的开发,如服务发现注册、配置中⼼、消息总线、负载均衡、断路器、数据监控等,都可以⽤ Spring Boot的开发⻛格…...

【NOI】C++程序结构入门之分支结构二
文章目录 前言一、逻辑运算符1.导入2.逻辑与(&&)3.逻辑或(||)4.逻辑非(!) 二、例题讲解问题:1656. 是两位的偶数吗问题:1658. 游乐设施问题:1659. 是否含有数字5…...

web自动化系列-使用普通模式编写测试用例以及存在问题(十六)
前面已经把selenium的主要操作介绍完毕 ,接下来我们通过编写几条测试用例感受下selenium的用法 。 1.用例需求 还是以登录为例 ,需要实现的测试用例为 : case1:输入正确的用户名和密码进行登录case2 : 输入正确的用户名和错误的…...

VSCode 配置 Qt 开发环境
文章目录 1. 环境说明2. 配置系统环境变量 1. 环境说明 操作系统:Windows 11VSCode版本:1.88.1CMake版本:3.27.7Qt6版本:6.7.0(MinGW 11.2.0 64-bit) 2. 配置系统环境变量 自行根据自己的Qt安装路径配置 配置 MinGW 和 CMake C…...
:Gitlab添加组、创建用户、创建项目和源码上传到Gitlab仓库)
【Jenkins】持续集成与交付 (七):Gitlab添加组、创建用户、创建项目和源码上传到Gitlab仓库
🟣【Jenkins】持续集成与交付 (七):Gitlab添加组、创建用户、创建项目和源码上传到Gitlab仓库 1、创建组2、创建用户3、将用户添加到组中4、在用户组中创建项目5、源码上传到Gitlab仓库5.1 初始化版本控制5.2 将文件添加到暂存区5.3 提交代码到本地仓库5.4 推送代码到 Git…...
L1-017 到底有多二
一个整数“犯二的程度”定义为该数字中包含2的个数与其位数的比值。如果这个数是负数,则程度增加0.5倍;如果还是个偶数,则再增加1倍。例如数字-13142223336是个11位数,其中有3个2,并且是负数,也是偶数&…...
常用语音识别开源四大工具:Kaldi,PaddleSpeech,WeNet,EspNet
无论是基于成本效益还是社区支持,我都坚决认为开源才是推动一切应用的动力源泉。下面推荐语音识别开源工具:Kaldi,Paddle,WeNet,EspNet。 1、最成熟的Kaldi 一个广受欢迎的开源语音识别工具,由Daniel Pove…...
python笔记 | 哥德巴赫猜想
哥德巴赫猜想:每个不小于6的偶数都可以表示成两个素数之和。 素数:只能被1和自身整除的正整数。就是大于1且除了1和它本身之外没有其他因数的数。例如,2、3、5、7、11等都是素数,而4、6、8、9等则不是素数。 下面这段Python代码…...

IO基础-IO多路复用基础
Java的Selector封装了底层epoll和poll的API,可以通过指定如下参数来调用执行的内核调用, 在Linux平台,如果指定 -Djava.nio.channels.spi.SelectorProvidersun.nio.ch.PollSelectorProvider 则底层调用poll, -Djava.nio.channels.spi.Selec…...

Python机器学习项目开发实战:如何进行人脸识别
注意:本文的下载教程,与以下文章的思路有相同点,也有不同点,最终目标只是让读者从多维度去熟练掌握本知识点。 下载教程: Python机器学习项目开发实战_人脸识别_编程案例解析实例详解课程教程.pdf 人脸识别是一个复杂但…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...
