python笔记 | 哥德巴赫猜想
哥德巴赫猜想:每个不小于6的偶数都可以表示成两个素数之和。
素数:只能被1和自身整除的正整数。就是大于1且除了1和它本身之外没有其他因数的数。例如,2、3、5、7、11等都是素数,而4、6、8、9等则不是素数。
下面这段Python代码验证6到1000以内的情况:
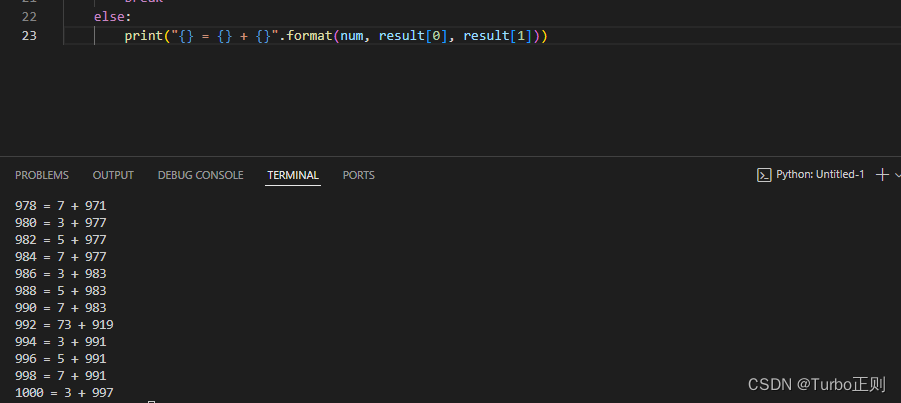
def is_prime(n):if n < 2:return Falsefor i in range(2, int(n ** 0.5) + 1):if n % i == 0:return Falsereturn Truedef goldbach_conjecture(num):for i in range(2, num):if is_prime(i):for j in range(i, num):if is_prime(j) and i + j == num:return (i, j)return Nonefor num in range(6, 1001, 2):result = goldbach_conjecture(num)if result is None:print("Goldbach conjecture is wrong.")breakelse:print("{} = {} + {}".format(num, result[0], result[1]))
先定义了一个判断素数的函数is_prime,然后定义了一个验证哥德巴赫猜想的函数goldbach_conjecture。goldbach_conjecture函数接受一个偶数作为参数,然后在2到这个偶数之间寻找两个素数,使它们的和等于这个偶数。如果找到了这样的两个素数,就返回它们;否则返回None。
最后,在6到1000之间的所有偶数上调用goldbach_conjecture函数,并输出结果。
相关文章:

python笔记 | 哥德巴赫猜想
哥德巴赫猜想:每个不小于6的偶数都可以表示成两个素数之和。 素数:只能被1和自身整除的正整数。就是大于1且除了1和它本身之外没有其他因数的数。例如,2、3、5、7、11等都是素数,而4、6、8、9等则不是素数。 下面这段Python代码…...

IO基础-IO多路复用基础
Java的Selector封装了底层epoll和poll的API,可以通过指定如下参数来调用执行的内核调用, 在Linux平台,如果指定 -Djava.nio.channels.spi.SelectorProvidersun.nio.ch.PollSelectorProvider 则底层调用poll, -Djava.nio.channels.spi.Selec…...

Python机器学习项目开发实战:如何进行人脸识别
注意:本文的下载教程,与以下文章的思路有相同点,也有不同点,最终目标只是让读者从多维度去熟练掌握本知识点。 下载教程: Python机器学习项目开发实战_人脸识别_编程案例解析实例详解课程教程.pdf 人脸识别是一个复杂但…...
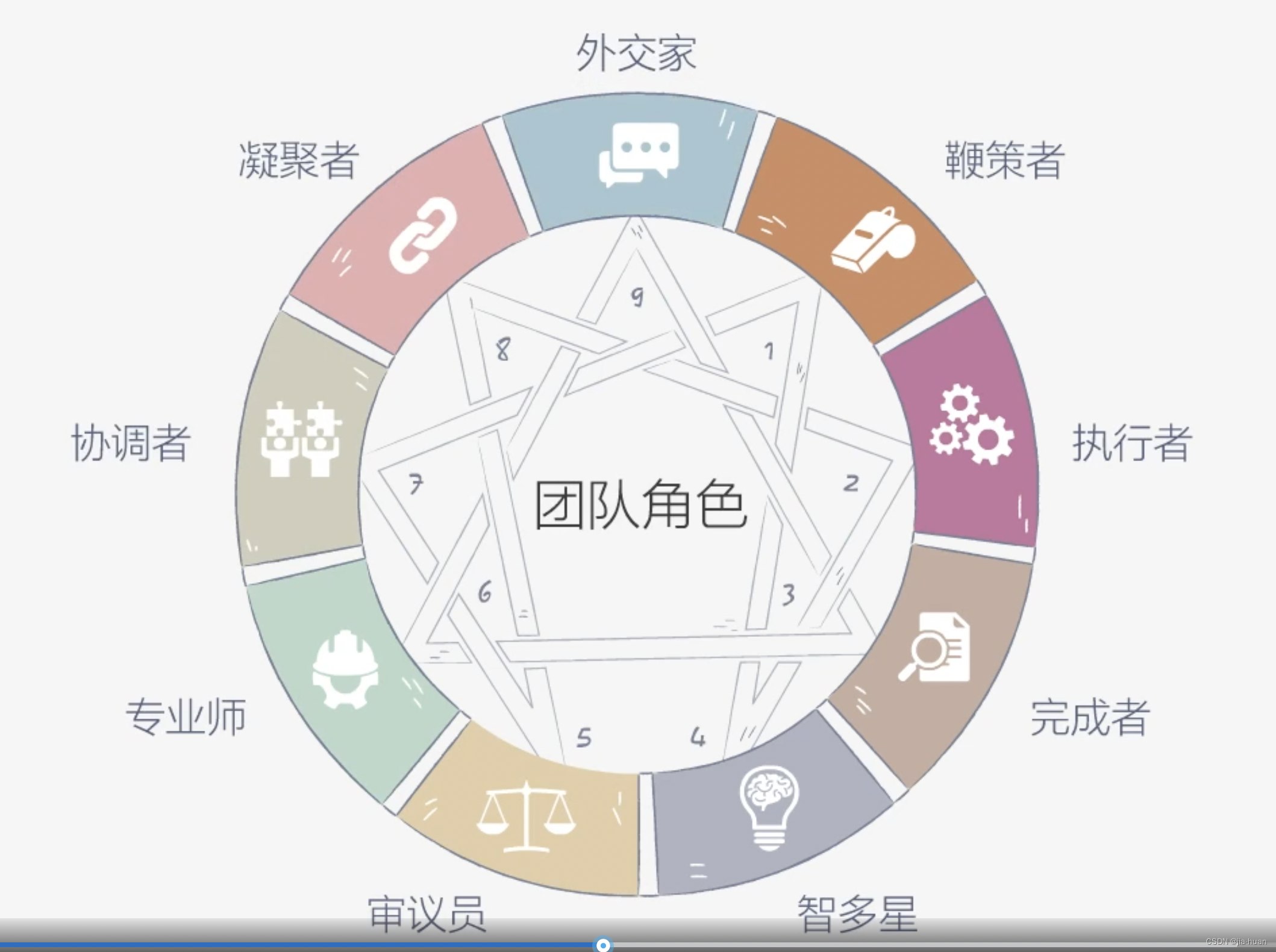
管理能力学习笔记五:识别团队角色,因才施用
识别团队角色,因才施用,需要做到以下三点 扬长避短 管理者要学会问自己员工能把什么做好,而不是想方设法改造他们的短处 。 – 彼得德鲁克 人岗匹配 将合适的人放在合适的位置 人才多样化 团队需要各式各样的人才,才能高效配合…...
Real3DPortrait照片对口型,数字人,音频/视频驱动数字人
先看效果 上传一张图片和一段音频,照片如下: 合成后效果如下: 照片对口型-音频驱动 支持音频驱动和视频驱动,视频可以使照片有参照视频中的口型和和动作。 项目地址 https://github.com/yerfor/Real3DPortrait 我的环境 win…...
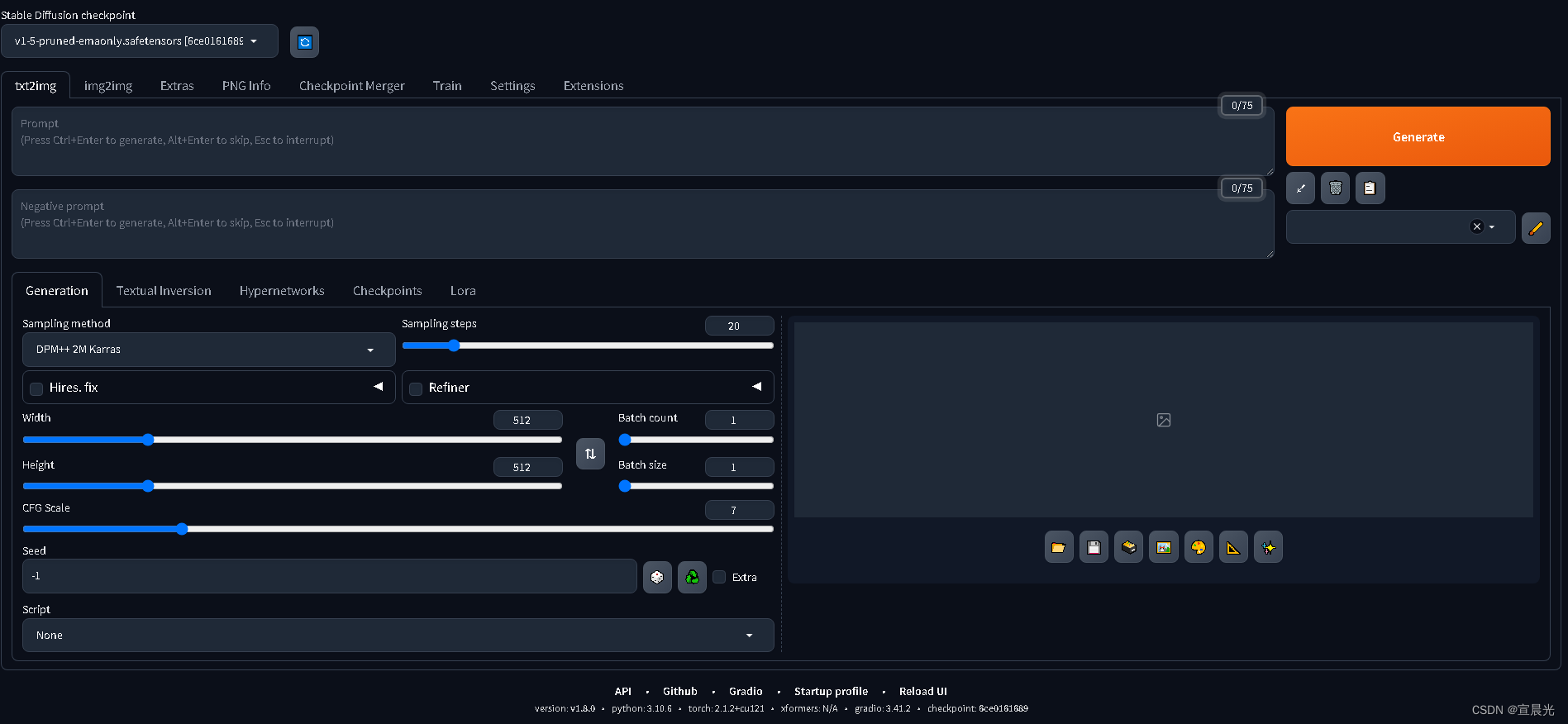
Stable Diffusion之Ubuntu下部署
1、安装conda环境 conda create -n webui python3.10.6 2、激活环境 每次使用都要激活 conda activate webui 注意开始位置的变换 关闭环境 conda deactivate webui 3、离线下载SD 代码 https://github.com/AUTOMATIC1111/stable-diffusion-webui https://github.com/Stabilit…...

LeetCode-15-三数之和问题
题目说明 给定一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a b c 0 ?找出所有满足条件且不重复的三元组。 注意:答案中不可以包含重复的三元组。 给定数组 nums [-1, 0,…...
springboot2集成东方通tongweb嵌入式版
由于最近项目需要国产化信创改造,引入东方通tongweb 联系东方通厂家 ,将依赖导入到maven仓库,并获取嵌入式版license文件修改pom.xml,引入依赖,注意springboot版本,这里以springboot2举例 首先移除springb…...

【二分查找】Leetcode 33. 搜索旋转排序数组【中等】
搜索旋转排序数组 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], num…...

Zephyr Windows开发环境搭建
Zephyr 如果有错误或未及时更新,请以官网文档为主 官网:https://docs.zephyrproject.org/latest/develop/getting_started/index.htm 下载安装 Chocolatey 这是一个类似于在Linux系统下 yum 和 apt 那样的包管理器 官网:https://chocolat…...

如何安全地设置MySQL数据库的IP白名单
设置MySQL数据库的IP白名单是一种关键的安全措施,可以确保只有来自特定IP地址的请求被允许访问数据库服务器。这里是如何安全地配置这些设置的分步指南。 步骤1: 登录到MySQL服务器 首先,使用管理员权限登录到你的MySQL服务器。如果你使用的是命令行&a…...

Chatgpt掘金之旅—有爱AI商业实战篇|品牌故事业务|(十六)
演示站点: https://ai.uaai.cn 对话模块 官方论坛: www.jingyuai.com 京娱AI 一、AI技术创业在品牌故事业务有哪些机会? 人工智能(AI)技术作为当今科技创新的前沿领域,为创业者提供了广阔的机会和挑战。随…...
为什么要部署IP SSL证书?怎么申请?
我们需要知道什么是IP SSL证书。SSL,全称为Secure Sockets Layer,即安全套接层,是为网络通信提供安全及数据完整性的一种安全协议。而IP SSL证书就是基于SSL协议的一种证书,它能够为网站和用户的数据传输提供加密处理,…...
最新免费 ChatGPT、GPTs、AI换脸(Suno-AI音乐生成大模型)
🔥博客主页:只恨天高 ❤️感谢大家点赞👍收藏⭐评论✍️ ChatGPT3.5、GPT4.0、GPTs、AI绘画相信对大家应该不感到陌生吧?简单来说,GPT-4技术比之前的GPT-3.5相对来说更加智能,会根据用户的要求生成多种内容…...

前端的未来已然到来
随着整个软件行业正逐渐转向以打包、托管与抽象解决方案为主体的新形态,后端与基础设施带来的麻烦正越来越少,而立足堆栈顶部的前端工程师开始成为施展空间最大的时代宠儿。甚至不只是他们,如今无论是前端、后端还是运维开发者,他…...

Open CASCADE学习|gp_XYZ与gp_Mat
gp_XYZ和gp_Mat是Open CASCADE Technology (OCCT)中的类,用于处理3D几何和变换。 gp_XYZ gp_XYZ类代表了一个三维空间中的点或向量。它通过三个坐标值(X, Y, Z)来定义位置或方向。这个类提供了多种操作,比如计算两点之间的距离、…...

BMS绝缘电阻检测原理【转】
...
优秀的测试开发工程师需要掌握哪些技能?
科技的发展与网络技术的广泛应用,让测试开发已成为软件开发过程中不可或缺的一环。测试开发工程师是为确保软件程序的质量和稳定性而工作的专业人士。但是成为一名合格的测试开发工程师需要具备哪些技能呢?一起来看看吧! 优秀的测试开发工程…...
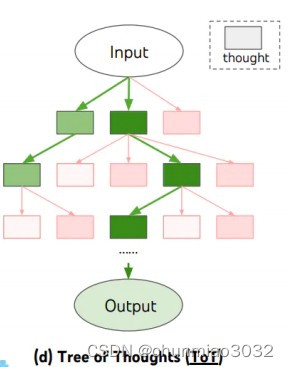
思维树(Tree of Thoughts)的概念
思维树(Tree of Thoughts,简称ToT)是一种利用大型语言模型进行问题解决的框架。这个框架借鉴了人类认知研究的成果,特别是关于人类在做决策时的两种思维方式:快速、自动、无意识的模式(称为“系统1”&#…...
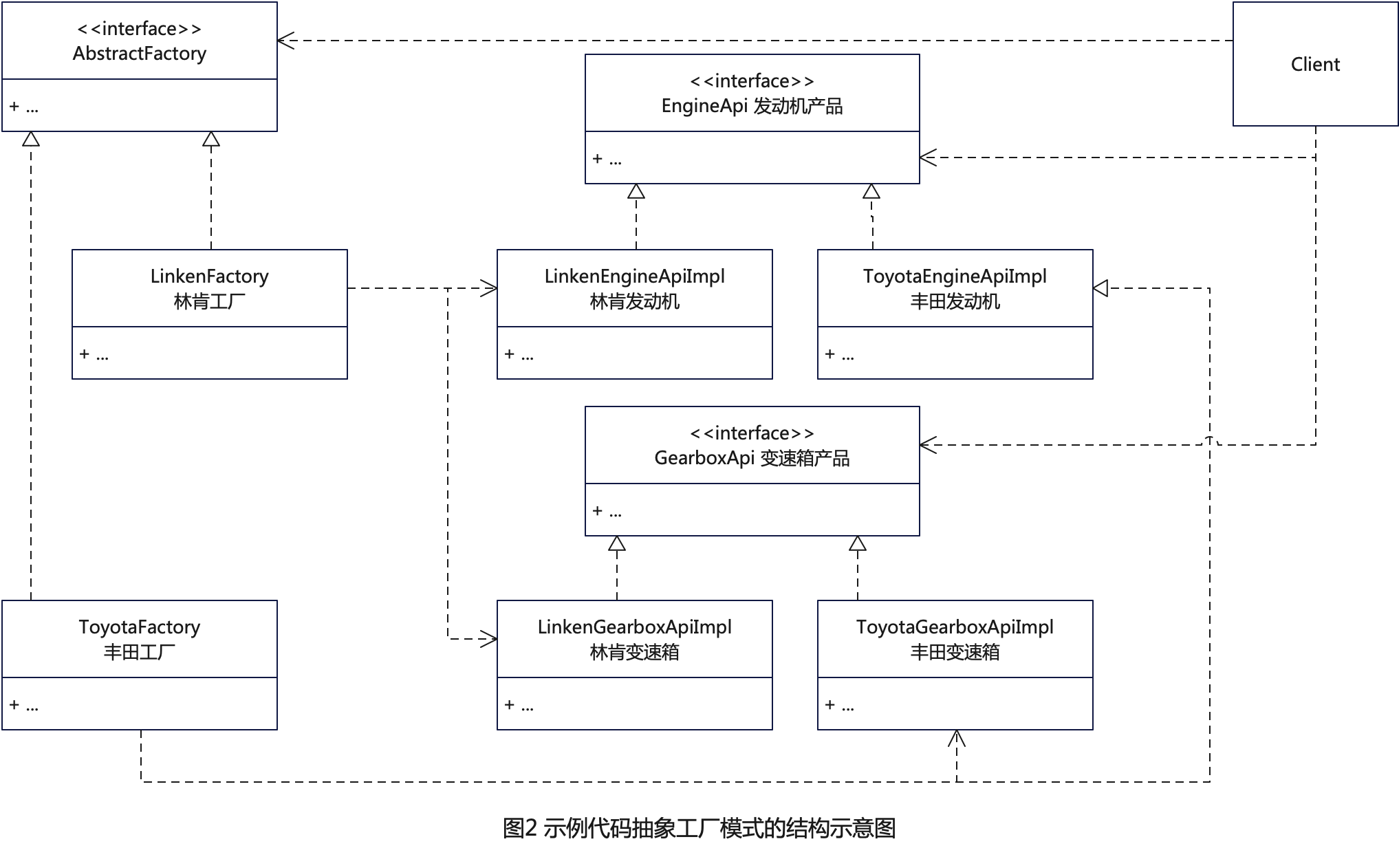
探索设计模式的魅力:抽象工厂模式的艺术
个人主页: danci_ 🔥系列专栏:《设计模式》《MYSQL应用》 💪🏻 制定明确可量化的目标,坚持默默的做事。 🚀 转载自文章:探索设计模式的魅力:抽象工厂模式的艺术 抽象工厂模式&…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...
