优化理论复习——(三)
本篇介绍无约束优化的问题,通过四种算法来进行求解的过程和思路,也是最优化方法中的最重要的一类问题。
无约束优化问题主要是通过迭代搜索算法来切结,比线性规划的计算量都小一点。
目录
- 无约束优化问题
- 最优性条件
- 最速下降法
- 牛顿法
- 共轭梯度法
- 拟牛顿法
无约束优化问题
最优性条件
首先是无约束优化问题的最优性条件,是必要条件,得是局部极小才有梯度=0和hesse阵半正定。

其次是充分条件:

无约束凸规划则可以直接有以下充要条件:

之前的学习中我们知道了线搜索迭代算法,这里把它用来计算最优值,一般思路如下:


接下来我们学习四种迭代算法的基本思路和性质:
最速下降法
最速下降法,这是因为负梯度方向是下降的最快的,顾名。

最速下降法具有全局收敛性。然后用精确一维线搜索时的步长为:

这里要求了二次正定函数。步长信息就是已知的。
牛顿法
然后是牛顿法,经典牛顿法步长为1:

注意,经典牛顿法不一定是下降方向,
所以计算hesse阵很重要。

经典牛顿法一般都不会让你一直求,这里注意一下,这里需要注意什么是二次终止性:


收敛上看,它是局部二阶收敛的:

由于经典牛顿法比较特殊,所以还是需要引入带线搜索的牛顿法,其中用精确一维线搜索时是阻尼牛顿法:

带线搜索的牛顿法具有全局收敛性和局部二阶收敛速度。
共轭梯度法
共轭有以下特征:


以下关于极小值的两个定理:


对于标准的二次函数使用共轭方向法就为:

这里面方向和步长就不一样了,方向是共轭方向,步长还是精确一维线搜索得到的步长。


拟牛顿法
拟牛顿法和牛顿法比较类似,不同的是用的是hesse阵是用H函数估计出来的:

也就是说他的迭代方向H(k)不再是hesse的逆矩阵,而是-H(K)g_k。

所以算法稍微复杂一点:

加入了一步计算H的,其余的相差不大。
理论性质方面,DFP算法的性质有:
首先是满足拟牛顿方程(H_k+1的表达式),同时产生的搜索方向是共轭方向。
然后也有二次终止性:

到此为止就介绍完了所有的无约束优化问题的内容。
相关文章:

优化理论复习——(三)
本篇介绍无约束优化的问题,通过四种算法来进行求解的过程和思路,也是最优化方法中的最重要的一类问题。 无约束优化问题主要是通过迭代搜索算法来切结,比线性规划的计算量都小一点。 目录 无约束优化问题最优性条件最速下降法牛顿法共轭梯度…...
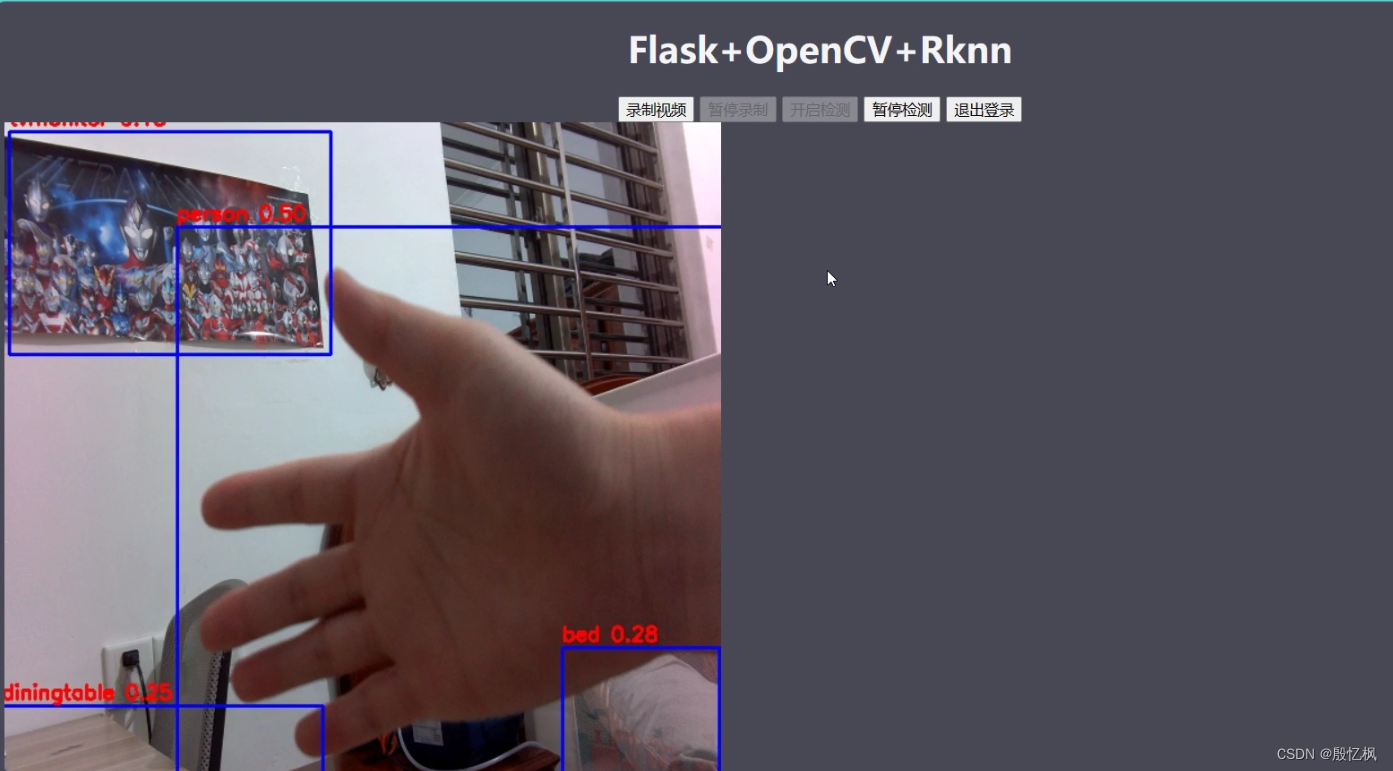
RK3568笔记二十四:基于Flask的网页监控系统
若该文为原创文章,转载请注明原文出处。 此实验参考 《鲁班猫监控检测》,原代码有点BUG,已经下载不了。2. 鲁班猫监控检测 — [野火]嵌入式AI应用开发实战指南—基于LubanCat-RK系列板卡 文档 (embedfire.com) 一、简介 记录简单的摄像头监…...

[Django 0-1] Core.Serializers 模块
Core.Serializers 模块 Django 序列化模块 模块结构 . ├── __init__.py ├── base.py ├── json.py ├── jsonl.py ├── python.py ├── pyyaml.py └── xml_serializer.py1 directory, 7 files自定义序列化器 通过继承django.core.serializers.base.Serial…...

鸿蒙内核源码分析(用栈方式篇) | 程序运行场地谁提供的
精读内核源码就绕不过汇编语言,鸿蒙内核有6个汇编文件,读不懂它们就真的很难理解以下问题. 1.系统调用是如何实现的? 2.CPU是如何切换任务和进程上下文的? 3.硬件中断是如何处理的? 4.main函数到底是怎么来的? 5.开机最开始发生了什么? 6.关机…...
Linux 进程间通信之匿名管道
💓博主CSDN主页:麻辣韭菜💓 ⏩专栏分类:Linux知识分享⏪ 🚚代码仓库:Linux代码练习🚚 🌹关注我🫵带你学习更多Linux知识 🔝 目录 前言 一. 进程间通信介绍 1.进程间通…...
)
数据结构与算法学习笔记六--数组和广义表(C语言)
目录 前言 1.数组 1.定义 2.初始化 3.销毁 4.取值 5.设置值 6.完整代码 前言 这篇博客主要介绍数据结构中的数组和广义表的用法。 1.数组 在数据结构中,数组是一种线性数据结构,它由一组连续的相同类型的元素组成,每个元素都有一个唯…...

图搜索算法详解
图搜索算法详解 摘要: 图搜索算法是解决路径规划和网络分析问题的关键技术。本文将详细介绍图搜索算法的基本概念、分类以及常见的算法,如广度优先搜索(BFS)、深度优先搜索(DFS)、A*搜索等。同时ÿ…...

安卓中常见的UI控件
TextView(文本视图)EditText(编辑文本)Button(按钮)ImageView(图像视图)ImageButton(图像按钮)CheckBox(复选框)RadioButtonÿ…...
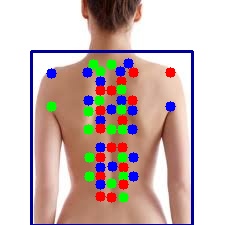
基于Labelme的背部穴位关键点制作
一、穴位定位方法 穴位定位,自春秋时期以来,通过各代医学实践的继承与发展,形成了一套较为科学的定位体系。这套体系基于经络理论,采用“寸”作为测量单位,按照人体比例来进行精确的穴位定位,主要有依据体…...
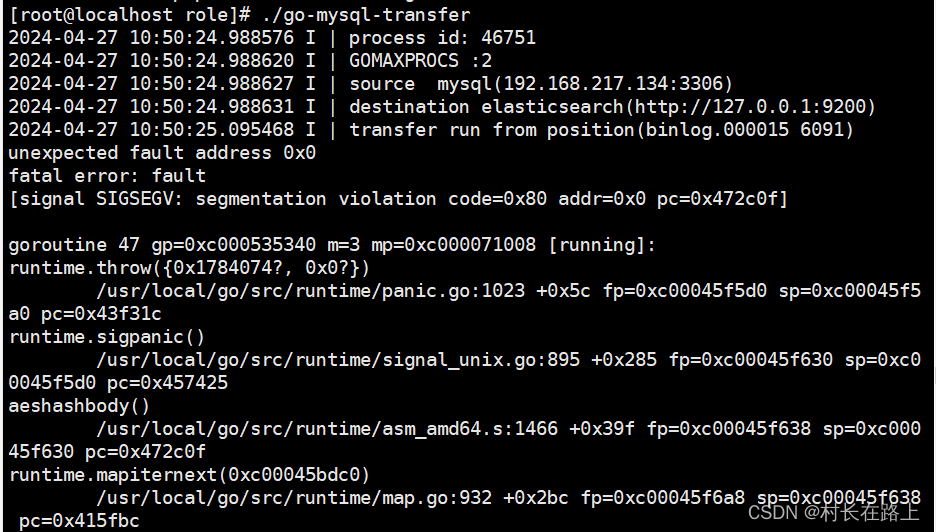
go-mysql-transfer 同步数据到es
同步数据需要注意的事项 前提条件 1 要同步的mysql 表必须包含主键 2 mysql binlog 必须是row 模式 3 不支持程序运行过程中修改表结构 4 要赋予连接mysql 账号的权限 reload, replication super 权限 如果是root 权限则不需要 安装 go-mysql-transfer git clone…...
外包干了3天,技术就明显退步了。。。。。
先说一下自己的情况,本科生,19年通过校招进入广州某软件公司,干了接近4年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了四年的功能测试…...

将要上市的自动驾驶新书《自动驾驶系统开发》中摘录各章片段 1
以下摘录一些章节片段: 1. 概论 自动驾驶系统的认知中有一些模糊的地方,比如自动驾驶系统如何定义的问题,自动驾驶的研发为什么会有那么多的子模块,怎么才算自动驾驶落地等等。本章想先给读者一个概括介绍,了解自动驾…...

String、StringBuilder、StringBuffer之间的区别是什么?
在Java中,String、StringBuilder 和 StringBuffer 是处理字符串的三个类,其中 String 是不可变对象,而 StringBuilder 和 StringBuffer 是可变对象。这些类在字符串操作方面具有不同的特性和用途。 String String 类表示不可变的字符序列&a…...
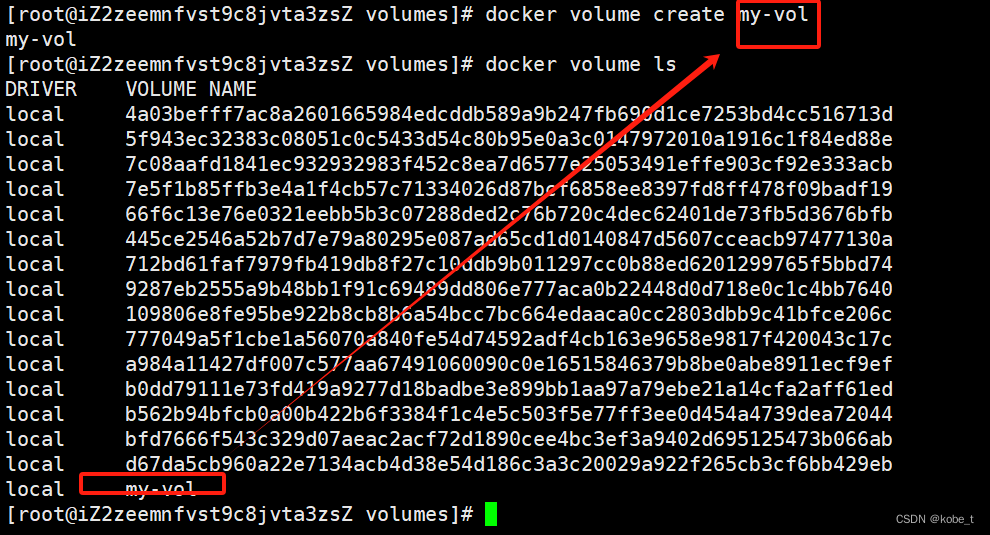
docker系列8:容器卷挂载(上)
目录 传送门 从安装redis说起 什么是容器卷挂载 操作系统的挂载 日志文件一般是"首恶元凶" 挂载命令 容器卷挂载 卷挂载命令 启动时挂载 查看挂载卷信息 容器卷管理 查看卷列表 创建容器卷 具名挂载与匿名挂载 具名挂载 传送门 docker系列1ÿ…...

痉挛性斜颈患者自己做哪些运动对脖子好?
痉挛性斜颈(Dystonia)是一种罕见的神经系统疾病,其特点是颈部肌肉痉挛,导致头部姿势异常倾斜或扭曲。而在治疗痉挛性斜颈中,运动疗法是非常重要的一部分。下面将介绍一些痉挛性斜颈患者可以自己进行的运动,…...
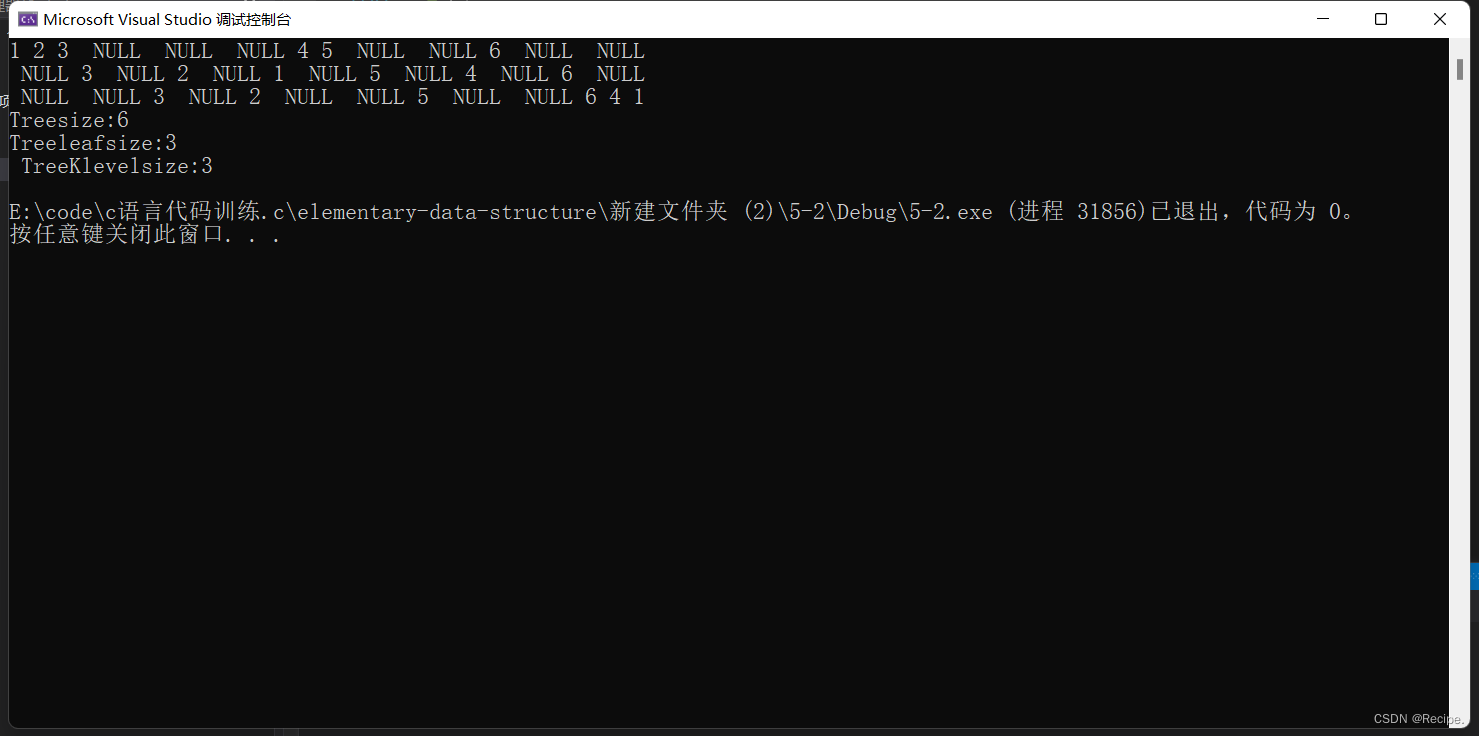
数据结构——二叉树链式结构的实现(上)
二叉树概念 再看二叉树基本操作前,再回顾下二叉树的概念, 二叉树是: 1. 空树 2. 非空:根节点,根节点的左子树、根节点的右子树组成的。 从概念中可以看出,二叉树定义是递归式的 二叉树构成࿱…...

数据结构内容概览
0. 绪论 绪论01——复杂度度量 绪论02——复杂度分析 绪论03——递归分析 绪论04——算法分析 绪论05——动态规划 算法设计与优化——前n项和计算 算法设计优化——对于任意非负整数,统计其二进制展开中数位1的总数 算法设计优化——Fibonacci数 算法设计优化——…...

当Linux系统运行时间长了之后,会出现磁盘空间不足提示,需要及时进行清理
Linux系统(CentOS 7)的磁盘空间不足时,可以采取以下步骤进行清理: 查找并删除大文件: 使用du和find命令可以找到并删除大文件。例如,要查找/目录下大于100MB的文件,可以运行: find /…...

【Flask 系统教程 4】Jinjia2模版和语法
Jinjia2 模板 模板的介绍 Jinja2 是一种现代的、设计优雅的模板引擎,它是 Python 的一部分,由 Armin Ronacher 开发。Jinja2 允许你在 HTML 文档中嵌入 Python 代码,以及使用变量、控制结构和过滤器来动态生成内容。它的语法简洁清晰&#…...
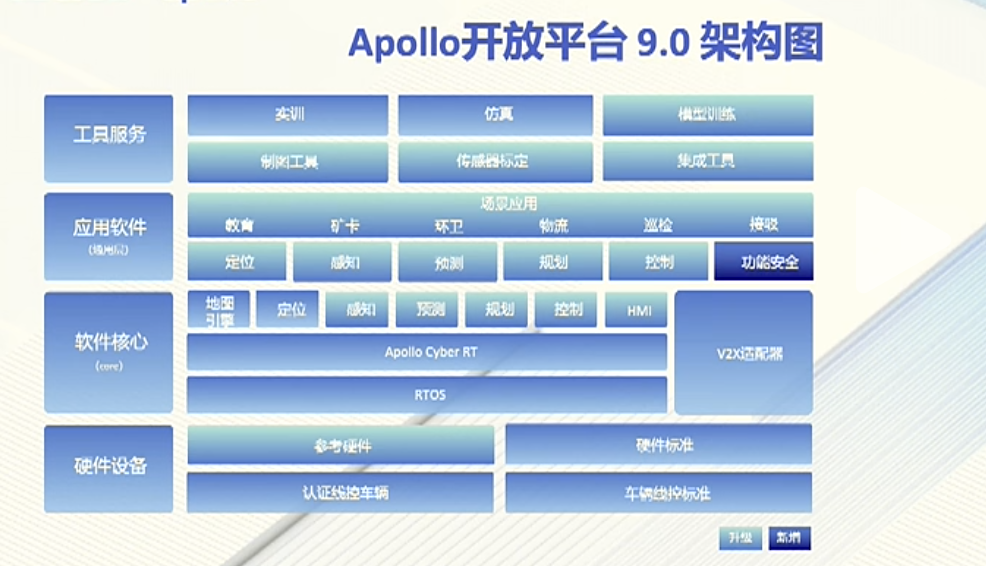
与 Apollo 共创生态:七周年大会心得
与 Apollo 共创生态:七周年大会心得 前言 4月19日,百度Apollo迎来七周年,历经七年的不懈追求与创新,Apollo开放平台已陆续推出了13个版本,汇聚了来自全球170多个国家与地区的16万名开发者及220多家合作伙伴。作为一名…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

HTML中各种标签的作用
一、HTML文件主要标签结构及说明 1. <!DOCTYPE html> 作用:声明文档类型,告知浏览器这是 HTML5 文档。 必须:是。 2. <html lang“zh”>. </html> 作用:包裹整个网页内容,lang"z…...
