Python氮氧甲烷乙烷乙烯丙烯气体和固体热力学模型计算
🎯要点
- 🎯固体和粒子:计算二态系统、简谐振子和爱因斯坦固体的内能和比热,比较爱因斯坦固体和德拜固体。模拟多个粒子的一维和二维随机游走,在数值上确认方差的线性趋势,模拟多个粒子的梯度下降,模拟双井的梯度下降。
- 🎯混合物:🖊建立理想气体及其混合物和多相纯物质的属性模型 。
- 🎯计算给定条件下的气体数值:🖊氮给定条件下的焦耳-汤姆逊系数 | 🖊气态氧流等熵效率的比功和出口气体温度 | 🖊液态水流量泵的冷却负荷和轴功率 | 🖊甲烷与十二烷合并流温度 | 🖊制冷剂经饱和蒸气压缩后的出口压力 | 🖊液氨储存罐安全体积 | 🖊氮气流过阀门哪一部分变成液体 | 🖊二氧化碳和氧气合流绝热压缩和等温压缩的压缩功率 | 🖊乙烯经两阀门膨胀后的温度 | 🖊蒸馏塔中塔压下降时泄漏率会如何变化 | 🖊丙烯储存容器加热后初始压力和最终温度 | 🖊氧气流被压缩机压缩后,压缩机功率和氧气出口温度 | 🖊热力循环水经过恒压加热、等熵膨胀、恒压冷凝和等熵压缩后的热效率 | 🖊计算甲烷焦耳-汤姆逊系数 | 🖊氨被压缩后,每摩尔压缩机的负荷和出口温度 | 🖊蒸汽压缩循环模拟。
- 🎯Python和C++物理计算热力学 | 🎯Python物理差分方程解
🍇Python水波纹偏微分方程
有一个不可否认的事实:波一直在我们周围。 无论是通过电磁辐射、空气中传播的声音,还是由一滴水引起的涟漪,波绝对无处不在。 尽管其形式多种多样,但在所有波浪中都适用的一件事是控制它们的严格物理规则。 在数学上,所有这些物理规则都浓缩为一个简单的微分方程之一:波动方程。
∂ 2 u ∂ t 2 = c 2 ( ∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 ) \frac{\partial^2 u}{\partial t^2}=c^2\left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}\right) ∂t2∂2u=c2(∂x2∂2u+∂y2∂2u)
波动方程告诉我们任何波如何在空间中传播并随时间演化,它为我们提供了函数 u(t, x, y),该函数给出了任意时间内任意点 (x, y) 处的波的高度 t。 本质上,如果你告诉波动方程,你把一个球扔进池塘,它会告诉你球产生的涟漪如何随着时间的推移而发展,并允许你预测由此引起的水的变化。 就像你告诉波动方程你尽可能大声尖叫一样,它会告诉你你创建的声波将如何传播并与环境相互作用。 总而言之,通过求解波动方程,我们将能够轻松模拟我们的纹波。
想象一下,两个人最初紧紧地握着一根绳子(红色),然后一个人快速上下移动手,在绳子上释放出波浪。在波穿过这条绳子后拍一张快照,我们想弄清楚它将如何随着时间的推移继续演化。 为了举例说明,我们假设一根无重力的无摩擦绳索。 为了开始解决这个问题,我们首先定义一些变量。
绳索在位置 x 和时间 t 处的高度将被称为函数 u(t, x) 的值。 考虑到这一点,我们要考虑什么可能会导致绳索随着时间的推移而发生变化。 由于我们确定不存在重力或摩擦力,因此作用在绳子上的唯一力就是张力,我们可以想象,张力在绳子的最小和最大高度处最大。
本质上,这是对凹度的陈述,因为张力在沿着绳索的高弯曲点处达到最高,并且随着远离这些点而减弱。 这里最终可以确定的是,在绳索上的任何给定点,它所承受的张力与其凹度成正比。 由于微积分告诉我们函数的凹性是由其在空间中的二阶导数定义的,因此我们可以将其表述为:
F tension = k ∂ 2 u ∂ x 2 F_{\text {tension }}=k \frac{\partial^2 u}{\partial x^2} Ftension =k∂x2∂2u
其中 k 是一个简单的比例常数。 现在我们必须找到一种方法,将力用 u 表示,并将其转化为我们可以解决和使用的东西。 研究牛顿第二定律,它告诉我们 F = ma,允许快速替换,结果为:
m a = k ∂ 2 u ∂ x 2 m a=k \frac{\partial^2 u}{\partial x^2} ma=k∂x2∂2u
其中 m 是该点的质量,a 是加速度,u 是高度,k 是比例常数。 正如物理学告诉我们的那样,任何处理位置的函数的加速度只是其相对于时间的二阶导数,这意味着我们可以将方程重新定义为:
∂ 2 u ∂ t 2 = k m ∂ 2 u ∂ x 2 \frac{\partial^2 u}{\partial t^2}=\frac{k}{m} \frac{\partial^2 u}{\partial x^2} ∂t2∂2u=mk∂x2∂2u
离散化波动方程
∂ 2 u ∂ t 2 = c 2 ( ∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 ) \frac{\partial^2 u}{\partial t^2}=c^2\left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}\right) ∂t2∂2u=c2(∂x2∂2u+∂y2∂2u)
在代码中,网格域将如下所示:
Lx = 10
Nx = 80
Ly = 10
Ny = 80 x_vec = numpy.linspace(0, Lx, Nx)
dx = x_vec[2] - x_vec[1] y_vec = numpy.linspace(0, Ly, Ny)
dy = y_vec[2] - y_vec[1]
dt 可以选择,这就是对我有用的数字,c 保持为 1 以保持方程简单。 dt 越小越好,因为它将导致更准确但更慢的模拟。
dt = .025
Nt = 4000
c = 1
u = numpy.zeros([Nt, len(x), len(y)])
如前所述,我们希望在池的中心出现扰动(中心为 (nx/2, ny/2)),因此 t-dt 和 t 的初始条件如下所示:
u[0, Nx // 2, Ny // 2] = numpy.sin(0)
u[1, Nx // 2, Ny // 2] = numpy.sin(1/10)
最后,要解决所有问题,我们要做的就是迭代时间并将所有值代入离散方程,从而得到:
for t in range(1, Nt-1):for x in range(1, Nx-1):for y in range(1, Ny-1):if (t < 100):u[t, Nx // 2, Ny // 2] = numpy.sin(t / 10)u[t+1, x, y] = c**2 * dt**2 * ( ((u[t, x+1, y] - 2*u[t, x, y] + u[t, x-1, y])/(dx**2)) + ((u[t, x, y+1] - 2*u[t, x, y] + u[t, x, y-1])/(dy**2)) ) + 2*u[t, x, y] - u[t-1, x, y]
现在您已经通过求解波动方程正式模拟了水波纹!只需迭代计算值并在代码中为每个步骤及时绘制一个曲面:
fig = pyplot.figure()
ax = fig.add_subplot(111, projection='3d')
X, Y = numpy.meshgrid(x_vec, y_vec)
for t in range(0, Nt):surf = ax.plot_surface(X, Y, u[t], color='b', shade=True,linewidth=0, antialiased=False)ax.view_init(elev=45)ax.set_zlim(-.0001, 2.4)pyplot.axis('off')pyplot.pause(.0001)pyplot.cla()
参阅一:计算思维
参阅二:亚图跨际
相关文章:

Python氮氧甲烷乙烷乙烯丙烯气体和固体热力学模型计算
🎯要点 🎯固体和粒子:计算二态系统、简谐振子和爱因斯坦固体的内能和比热,比较爱因斯坦固体和德拜固体。模拟多个粒子的一维和二维随机游走,在数值上确认方差的线性趋势,模拟多个粒子的梯度下降࿰…...

2024-04-30 区块链-以太坊-相关文档
摘要: 2024-04-30 区块链-以太坊-文档 以太坊-相关文档: https://github.com/ethereum/go-ethereum https://geth.ethereum.org/ https://geth.ethereum.org/docs https://ethereum.org/zh/ 以太坊开发文档 | ethereum.org 以太坊开发文档_w3cschool 以太坊开发文档 基础主题 …...

你用过最好用的AI工具有哪些?
你用过最好用的AI工具有哪些? 人工智能(AI)工具正在逐渐成为我们日常生活中不可或缺的助手,它们通过提供智能化服务,极大地提升了我们的工作效率和生活质量。以下是一些广泛使用的AI工具和应用,以及它们所…...
Amine-PEG-Amine,956496-54-1在生物成像、生物传感器等领域具有广泛的应用
【试剂详情】 英文名称 Amine-PEG-Amine,NH2-PEG-NH2 中文名称 氨基-聚乙二醇-氨基,氨基PEG氨基, 双端氨基聚乙二醇 CAS号 956496-54-1 外观性状 由分子量决定,液体或者固体 分子量 0.4k,0.6k,1k&…...
”)
为什么深度学习中减小泛化误差称为“正则化(Regularization)”
深度学习的一个重要方面是正则化(Regularization),Ian Goodfellow在《Deep Learning 》称正则化(Regularization)就是减小泛化误差。那么,为什么减小泛化误差称为正则化呢? 首先看正则化——Re…...
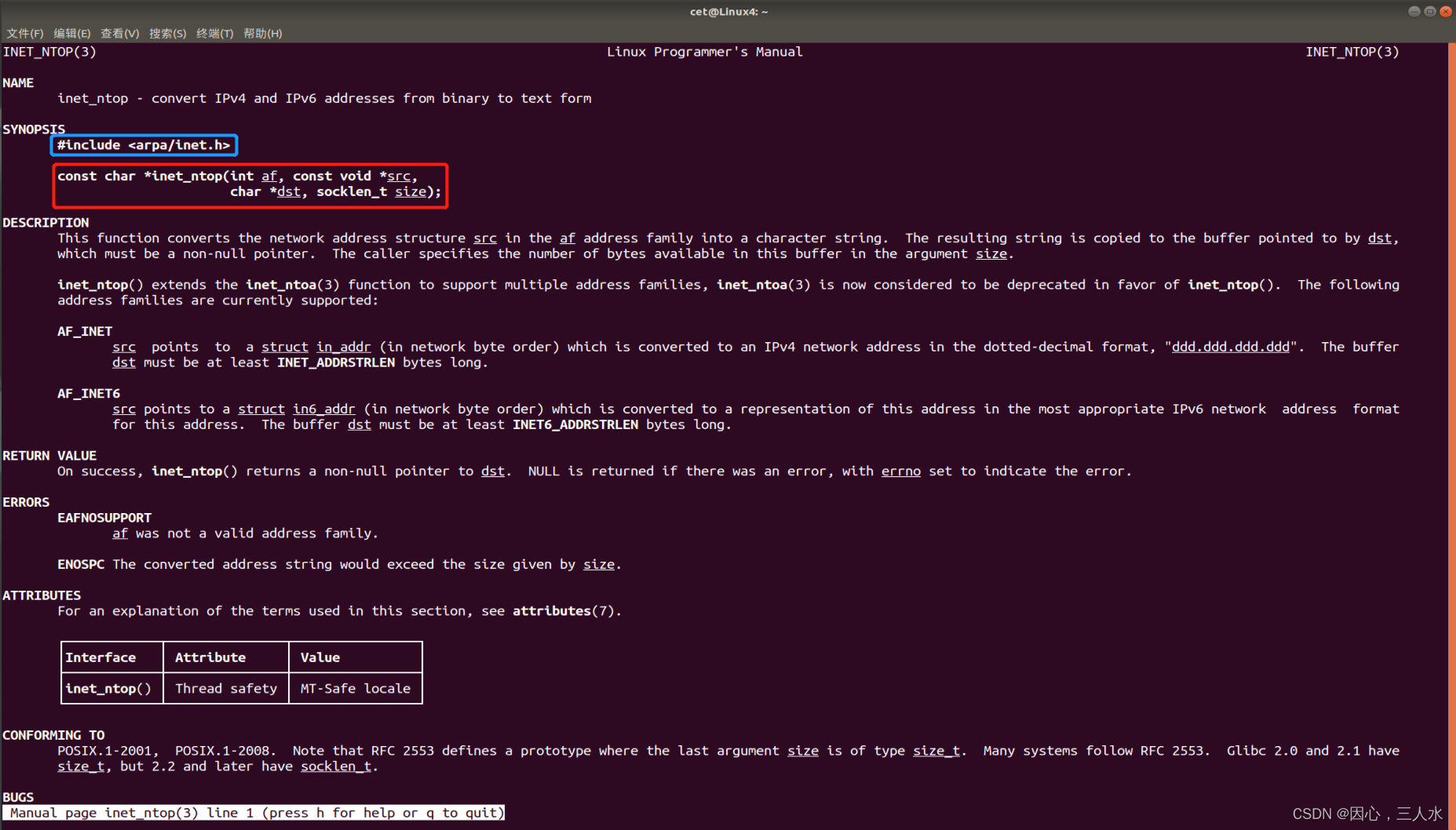
【Linux网络编程】2.套接字、网络字节序、IP地址转换函数
目录 网络套接字 网络字节序 网络字节序和主机字节序的转换 IP地址转换函数 inet_pton 参数af 参数src 参数dst 返回值 inet_ntop 参数af 参数src 参数dst 参数size 返回值 网络套接字 socket,一个文件描述符指向一个套接字,该套接字内部…...
代码签名证书的工作原理和申请流程
随着软件分发渠道的多样化和黑客攻击手段的不断升级,确保软件的真实性和完整性变得尤为重要。这正是代码签名证书(Code Signing Certificate)发挥关键作用的领域。本文将深入探讨代码签名证书的基础概念、工作原理、重要性以及申请和使用流程…...

Python中的yield
文章目录 1. Python中的yield1.1 一个简单的示例1.2 示例的每一步含义 2. yield 和return的区别2.1 一个简单的示例2.2 示例中每一步的含义 3. yield中的send()方法3.1 一个简单的示例3.2 示例中每一步的含义 4. yield中的throw()方法4.1 一个简单的示例4.2 示例中每一步的含义…...

【Linux】基于 Jenkins+shell 实现更新服务所需文件 -->两种方式:ssh/Ansible
👨🎓博主简介 🏅云计算领域优质创作者 🏅华为云开发者社区专家博主 🏅阿里云开发者社区专家博主 💊交流社区:运维交流社区 欢迎大家的加入! 🐋 希望大家多多支…...

5月4(信息差)
🎄 HDMI ARC国产双精度浮点dsp杜比数码7.1声道解码AC3/dts/AAC环绕声光纤、同轴、USB输入解码板KC33C 🌍 国铁集团回应高铁票价将上涨 https://finance.eastmoney.com/a/202405043066422773.html ✨ 源代码管理平台GitLab发布人工智能编程助手DuoCha…...

【Spring】1.Spring中IOC与DI全解析
本节将详细介绍Spring框架的两个核心概念:控制反转(IOC)和依赖注入(DI)。首先,我们会探讨IOC和DI的定义,实现原理,优点和缺点。然后,我们将介绍如何在Spring中使用IOC和D…...
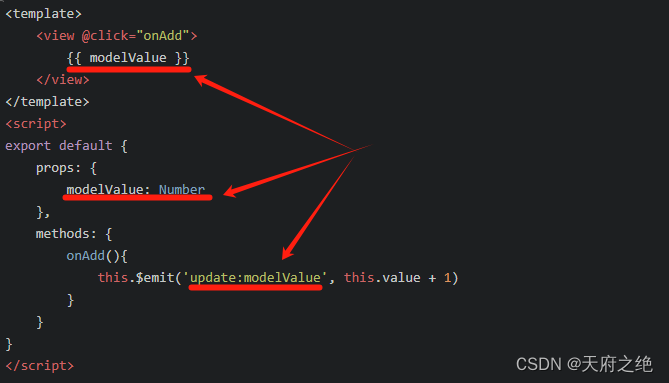
vue2迁移到vue3,v-model的调整
项目从vue2迁移到vue3,v-model不能再使用了,需要如何调整? 下面只提示变化最小的迁移,不赘述vue2和vue3中的常规写法。 vue2迁移到vue3,往往不想去调整之前的代码,以下就使用改动较小的方案进行调整。 I…...

【C语言】解决不同场景字符串问题:巧妙运用字符串函数
🌈个人主页:是店小二呀 🌈C语言笔记专栏:C语言笔记 🌈C笔记专栏: C笔记 🌈喜欢的诗句:无人扶我青云志 我自踏雪至山巅 文章目录 一、字符函数1.1 字符分类函数1.1.1 islower1.1.2 isupper 1.…...

android 如何显示网络地址对应的图片
1.android 如何显示网络地址对应的图片 在Android中显示网络地址对应的图片,通常有多种方法可以实现。以下是几种常见的方法: 1. 使用ImageView和Picasso库 Picasso是一个强大的图片加载库,它可以方便地加载网络图片并显示到ImageView中。 …...
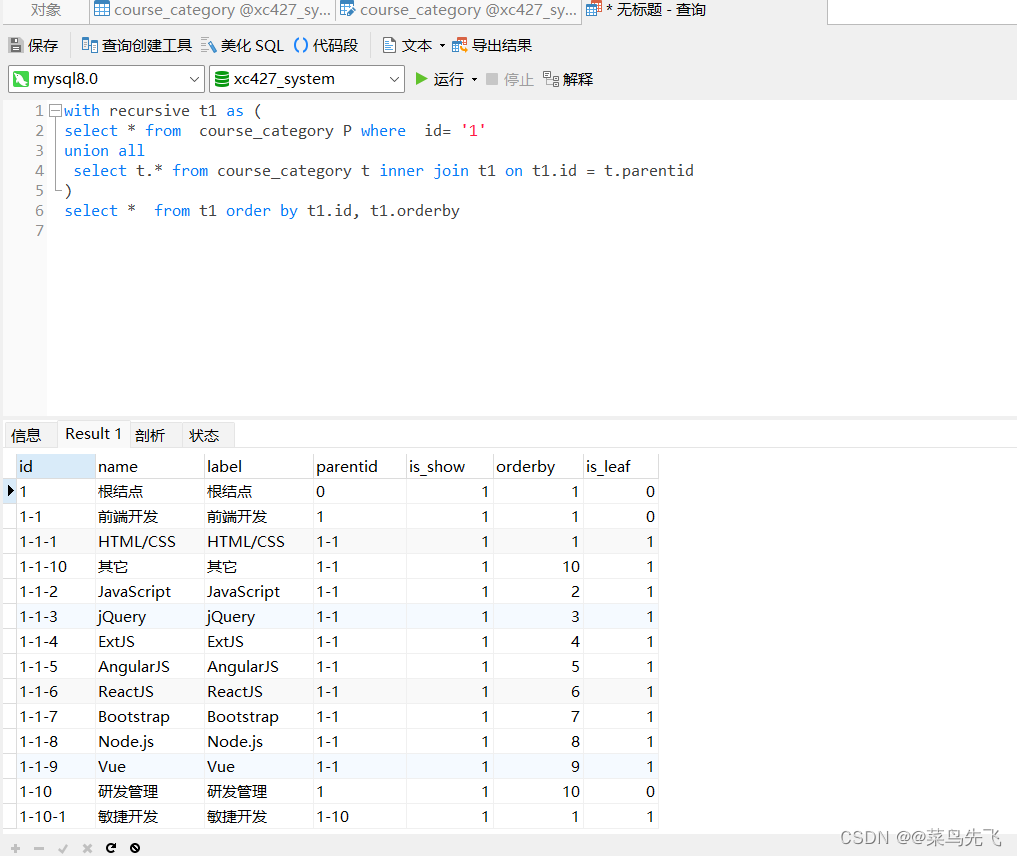
【项目学习01_2024.05.02_Day04】
学习笔记 4 课程分类查询4.1需求分析4.2 接口定义4.3 接口开发4.3.1 树型表查询4.3.2 开发Mapper 4 课程分类查询 4.1需求分析 有课程分类的需求 course_category课程分类表的结构 这张表是一个树型结构,通过父结点id将各元素组成一个树。 利用mybatis-plus-gen…...

Android SQLite中的UNIQUE constraint failed错误
报错信息: UNIQUE constraint failed SQLite中的UNIQUE constraint failed错误,表明尝试插入或更新数据库时出现了违反唯一性约束的情况。唯一性约束确保在特定列或列集合中的值在表中是唯一的,即不能有重复的值。当你尝试插入或更新已存在于…...

嘴尚绝卤味:传承经典,缔造美食新风尚
卤味,作为中国传统美食的代表之一,历经千年的传承与发展,早已成为无数食客餐桌上的宠儿。而在这个美食盛行的时代,嘴尚绝卤味凭借其独特的口感和精湛的工艺,成为卤味市场中的佼佼者,引领着卤味文化的新潮流…...
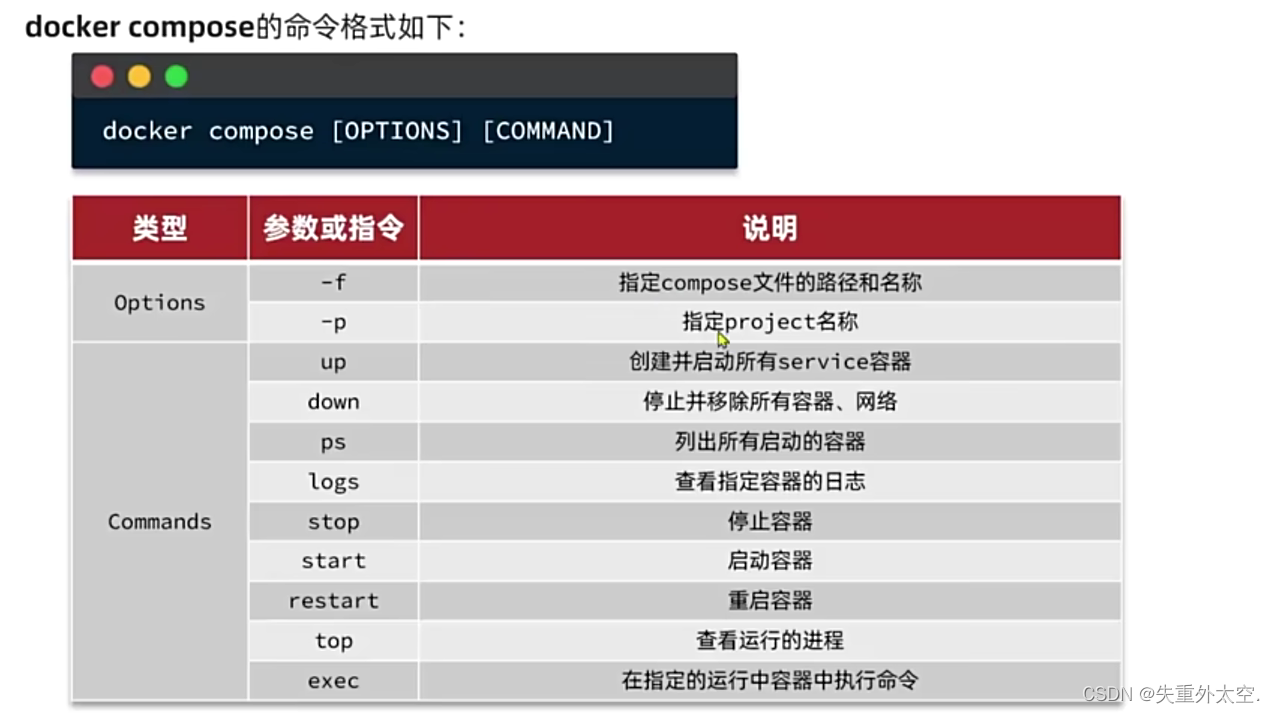
Docker 入门与实践:从零开始构建容器化应用环境
Docker 一、docker常用命令docker ps 格式化输出Linux设置命令别名 二、数据卷相关命令挂载到默认目录(/var/lib/docker)挂载到本地目录 三、自定义镜像Dockerfile构建镜像的命令 四、网络自定义网络 五、DockerCompose相关命令 一、docker常用命令 dock…...

C# 用户控件UserControl事件解绑资源释放
用户控件继承子 UserControl 。 现在有个业务需求在UserControl 所在的窗体关闭时解除事件HMouseDown绑定。 因没有相关的Close事件。后来本人想了一个办法在 ROICtlDesigner类的 Dispose 方法中执行相关的释放代码 比如解除事件绑定 释放资源 public partial class ROICt…...
QT-QTCreator环境配置
准备工作: 下载QT: 链接:https://pan.baidu.com/s/1prJcsC4DGqhKiXvLuPQFVA?pwd60b3 提取码:60b3下载WindowsKits: 链接:https://pan.baidu.com/s/1QNiS3HpbH5M5kXx5AhkqnQ?pwde2h8 提取码:e2h8安装的…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...
