实验四:搜索
实验四:搜索
1.填格子
题目描述
有一个由数字 0、1 组成的方阵中,存在一任意形状的封闭区域,封闭区域由数字1 包围构成,每个节点只能走上下左右 4 个方向。现要求把封闭区域内的所有空间都填写成2
输入要求
每组测试数据第一行一个整数 n(1≤n≤30)
接下来 n 行,由 0 和 1 组成的 n×n 的方阵。
封闭区域内至少有一个0 。
输出要求
已经填好数字 2 的完整方阵。
注意矩阵的每个数字后面都有一个空格
输入样例
6
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 0 0 1
1 1 0 0 0 1
1 0 0 0 0 1
1 1 1 1 1 1
输出样例
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 2 2 1
1 1 2 2 2 1
1 2 2 2 2 1
1 1 1 1 1 1
#include <iostream>
#include <queue>
using namespace std;queue<int>x;//初始化队列x来存储横坐标
queue<int>y;//初始化队列y来存储纵坐标int matrix[31][31];
int visited[31][31]={0};//visited用来记录元素是否被访问过int delta_x[4]={0,-1,0,1};//delta_x和delta_y用来进行广搜,来搜索对应元素的上下左右
int delta_y[4]={1,0,-1,0};int main()
{int N;cin>>N;for(int i=1;i<=N;i++){//从数组的索引1位置开始输入,外圈补一圈0for(int j=1;j<=N;j++){cin>>matrix[i][j];}}x.push(0);//将(0,0)坐标入队列y.push(0);visited[0][0]=1;int x1,y1;while(!x.empty()){for(int i=0;i<4;i++){//遍历对应元素的上下左右位置x1 = x.front()+delta_x[i];y1 = y.front()+delta_y[i];//如果满足没有越界且是0元素且没有被访问过if(x1>=0 && x1<=N+1 && y1>=0 && y1<=N+1 && matrix[x1][y1]==0 && visited[x1][y1]==0){x.push(x1);//则将对应的元素入队y.push(y1);visited[x1][y1]=1;} }x.pop();y.pop();}for(int p=1;p<=N;p++) {for(int q=1;q<=N;q++) {if(visited[p][q]==0 && matrix[p][q]==0){//如果元素没有被访问过,且为0元素cout<<2<<' '; }else{cout<<matrix[p][q]<<' '; } }cout<<endl;}return 0;
}
2.N皇后
题目描述
N皇后的排列,每行一个不冲突;N<=13。

输入要求
一个数字N (6 <= N <= 13) 表示棋盘是N x N大小的。
输出要求
前三行为前三个解,每个解的两个数字之间用一个空格隔开。第四行只有一个数字,表示解的总数。
解的输出顺序为从上到下从左到右,小的优先输出
输入样例
6
输出样例
2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4
#include <iostream>
#include <cmath>
using namespace std;
//用result来保存结果,result[i]=p表示棋子放在第i行第p列
int result[15];
//定义一个函数用来判断棋子放在当前行第p列是否合法
int is_place(int p)
{for(int i=1;i<p;i++){//对于前面p-1行来说if((result[i]==result[p]) || (abs(result[i]-result[p])==abs(i-p))){//不合法情况:在同一列或者在斜线上return 0;}}return 1;
}
// 定义函数求解N皇后问题
void Queen(int n)
{int p=1,ans=0,count=1;result[p]=1;//初始化:从第一行第一列开始放while(p>0){//对于第p行来说if(p<=n && result[p]<=n){//如果行列都没有超出矩阵范围if(is_place(p)==0){//当前列不合法result[p]=result[p]+1;//放到下一个位置}else{//当前列合法p=p+1;//到下一列去result[p]=1;//下一列从1开始}}else{//如果行列超出了索引范围,回溯if(p>n){//得到一个正确答案ans=ans+1;//正确答案数目加1if(count<=3){for(int j=1;j<n;j++){//输出一条正确答案cout<<result[j]<<" ";}cout<<result[n];cout<<endl;count++;}}p=p-1;//回到上一行result[p]=result[p]+1;//上一行的棋子往右走}}cout<<ans<<endl;
}
int main()
{int N;cin>>N;Queen(N);return 0;
}
3.再填格子
题目描述
有一个由数字 0、1 组成的方阵中,存在一任意形状的封闭区域,封闭区域由数字1 包围构成,每个节点只能走上下左右 4 个方向。现要求只把**【最大封闭区域】**内的空间填写成2 。
例如: 6×6 的方阵:
6
0 1 0 0 0 0
1 0 1 1 1 1
0 1 1 0 0 1
1 1 0 0 0 1
1 0 0 0 0 1
1 1 1 1 1 1
填写后如下:
0 1 0 0 0 0
1 0 1 1 1 1
0 1 1 2 2 1
1 1 2 2 2 1
1 2 2 2 2 1
1 1 1 1 1 1
输入要求
每组测试数据第一行一个整数 n(1≤n≤30)
接下来 n 行,由 0 和 1 组成的 n×n 的方阵。
封闭区域内至少有一个0,测试数据保证最大区域只有一个。
输出要求
已经填好数字 2 的完整方阵。(每个数字后面有一个空格!)
输入样例
6
0 1 0 0 0 0
1 0 1 1 1 1
0 1 1 0 0 1
1 1 0 0 0 1
1 0 0 0 0 1
1 1 1 1 1 1
输出样例
0 1 0 0 0 0
1 0 1 1 1 1
0 1 1 2 2 1
1 1 2 2 2 1
1 2 2 2 2 1
1 1 1 1 1 1
#include<iostream>
#include<cstring>using namespace std;
int a[40][40];
int n;
int dir[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; // 右 左 下 上
int cnt = 0; // 某一个封闭区域的大小
int maxn = 0; // 最大封闭区域大小
int id = 3; // 染色区域的编号
int max_id = id;
void dfs(int x, int y)
{if(x<0 || x>n+1 || y<0 || y>n+1 || a[x][y]!=0) //禁止染色的判断 x<0 || x>n+1 || y<0 || y>n+1为矩阵4个边return ;a[x][y] = id; //染色cnt++;for(int i=0; i<4; i++){dfs(x+dir[i][0], y+dir[i][1]);}
}
int main()
{cin >> n;memset(a, 0, sizeof(a)); int i;// 输入数据 for( i=1; i<=n; i++)for(int j=1; j<=n; j++){int k;cin >> k;a[i][j] = k;}//将边缘的0和其连接块都染色dfs(0, 0);id++;for( i=2; i<n; i++)for(int j=2; j<n; j++){cnt = 0;// 搜索每一个元素,找到最大封闭区域 dfs(i, j);//cout << cnt;if(cnt > maxn){maxn = cnt;max_id = id;}id++;}
// 输出
for( i=1; i<=n; i++)
{for(int j=1; j<=n; j++){if(a[i][j] == 1)cout << a[i][j] << " ";else if(a[i][j] != max_id)cout << '0' << " ";else cout << '2' << " ";} cout << endl;}return 0;
}
4.地图着色
题目描述
地图着色问题:如果把每一个区域收缩为一个顶点,把相邻两个区域用一条边相连接,就可以把一个区域图抽象为一个平面图。用m种颜色为图中的每个顶点着色,要求每个顶点着一种颜色,并使相邻两顶点之间有着不同的颜色。运用回溯法解决该问题。
输入要求
顶点数 颜色数
邻接矩阵
输出要求
着色方案
输入样例

输出样例

#include<iostream>
#include<stdio.h>
using namespace std;
int c[100][100]; //邻接矩阵
int color[100]; //记录每个顶点的颜色
int count,m,n; //count记录方案数 n个顶点 m种颜色
int Check(int k) //检查第i个顶点的颜色是否满足条件
{for(int i=1;i<=k;i++){if(c[k][i]==1&&color[i]==color[k]) //k与i之间相连并且i顶点的颜色与k顶点的颜色相同return 0;}return 1;
}
void GraphColor(int step)
{if(step==n+1) //表示前面所有的顶点颜色都已经填完{for(int i=1;i<=n;i++)printf("%d ",color[i]);count++;printf("\n");return ;}else{for(int i=1;i<=m;i++){color[step]=i; //首先将这个顶点颜色换为iif(Check(step)==1) //检查是否符合条件{GraphColor(step+1); //符合条件则走下一步}color[step]=0; //回溯 置为0}}
}
int main(void)
{printf("请输入顶点数:");scanf("%d",&n);printf("\n");printf("请输入颜色数:");scanf("%d",&m);printf("\n");printf("请输入邻接矩阵:\n");for(int i=1;i<=n;i++)for(int j=1;j<=n;j++){cin>>c[i][j];}printf("\n方案如下:\n");GraphColor(1);printf("\n");printf("%d",count);return 0;
}
相关文章:

实验四:搜索
实验四:搜索 1.填格子 题目描述 有一个由数字 0、1 组成的方阵中,存在一任意形状的封闭区域,封闭区域由数字1 包围构成,每个节点只能走上下左右 4 个方向。现要求把封闭区域内的所有空间都填写成2 输入要求 每组测试数据第一…...
本地开发vue项目联调遇到访问接口跨域问题
本地开发vue项目联调遇到访问接口跨域问题 修改本地的localhost 一:按winr打开运行窗口,输入drivers ,然后回车 二:打开etc文件夹,然后用记事本的方式打开里面的hosts文件, 三:这时我们就可…...
Vue键盘事件的使用
前言 在vue中,我们经常会用到键盘事件,不管是我们按下某个键,其实都是一次键盘事件的调用,下面就介绍下Vue中的键盘事件 先写一段代码,这里我选择的键盘事件是keyup,当然用keydown也是没问题的 问题来了,…...
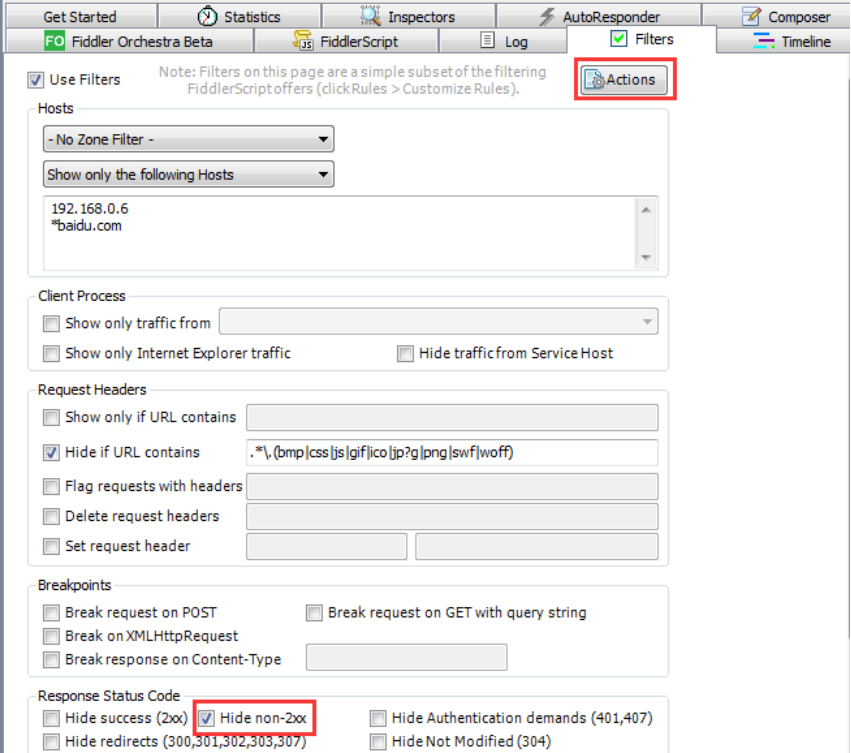
抓包工具fiddler详细使用教程
各位做测试的同学想必对抓包工具fiddler并不陌生,但是很多同学可能没有总结过它的用法,下面我总结了fiddler一些常用的用法。 Web端抓包配置 打开Fiddler,Tools -> Fiddler Options -> HTTPS 配置完后记得要重启Fiddler 选中Decrpt …...
raspberry Pi 连接蓝牙(小爱同学)
参数valueraspberry pi MOdel4B,4Gbbluetooth MOdel小爱同学writeTime2023年 2月11日 下午13:14分raspberry System ModelLinux raspberrypi 5.15.61-v8 #1579 SMP PREEMPT Fri Aug 26 11:16:44 BST 2022 aarch64 GNU/Linux 连接蓝牙 请在小爱同学app上…...
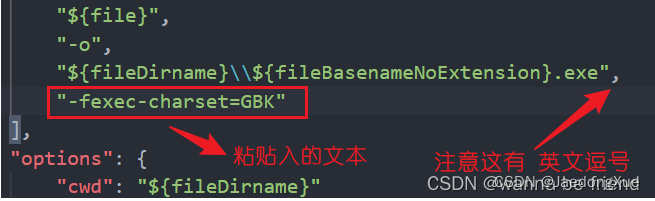
解决launch:program .exe does not exist
二. 程序的运行和调试 1.launch.json 复制下列代码至launch.json,并根据指导做出相对/绝对路径修改 用 IntelliSense 了解相关属性。 {// 使用 IntelliSense 了解相关属性。 // 悬停以查看现有属性的描述。// 欲了解更多信息,请访问: https://go.micros…...
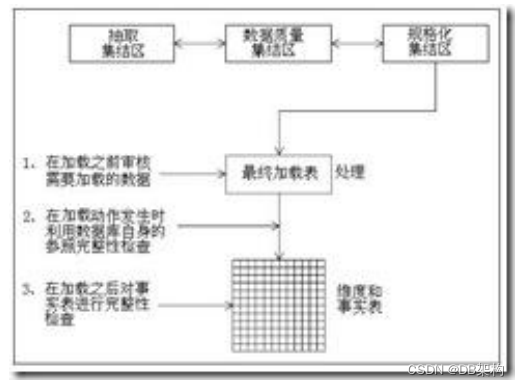
ETL --事实表
每一个事实表通过表的粒度来定义。事实表的粒度是事件度量的定义。我们必须至始至终按照度量如何在 现实世界中理解来规定事实表的粒度。 所有的事实表包含了一组关联到维表的外键,而这些维表提供了事实表度量的上下文。大多数的事实表还 包括了一个或者多个数值型…...
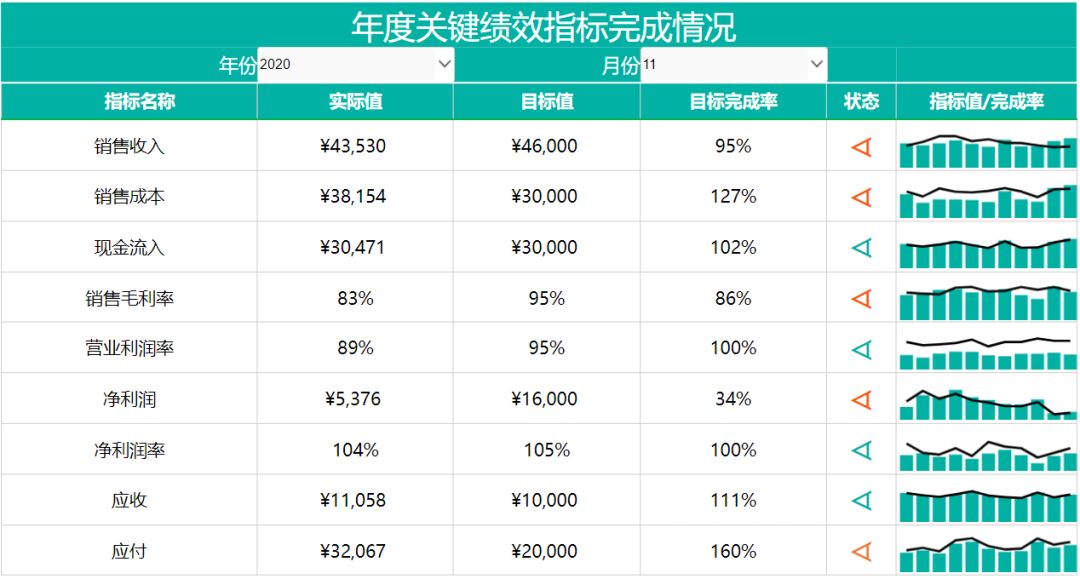
手工数据采集耗时耗力?Smartbi数据填报实现数据收集分析自动化
企业在日常经营管理过程中,往往需要收集很多内外部的信息,清洗整理后再进行存储、分析、呈现、决策支持等各种作业,如何高效收集结构化数据是企业管理者经常要面对的问题。传统手工的数据采集方式不仅耗费了大量人力时间成本,还容…...
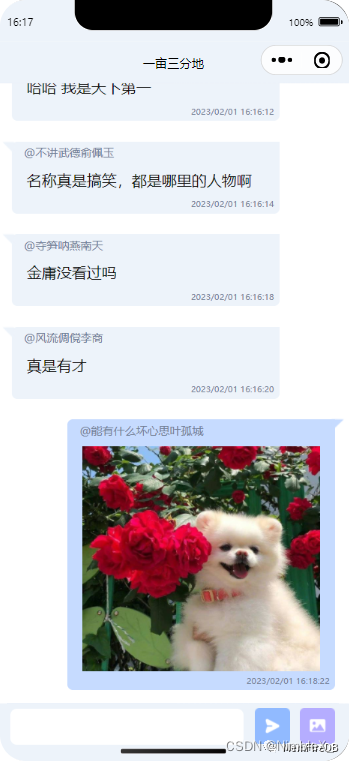
应用实战|微信小程序开发示例--多人聊天互动空间
“超能力”数据库~拿来即用,应用开发人员再也不用为撰写API而发愁。MemFire Cloud 为开发者提供了简单易用的云数据库(表编辑器、自动生成API、SQL编辑器、备份恢复、托管运维),很大地降低开发者的使用门槛。 本示例是…...

css:使用filter和backdrop-filter实现高斯模糊效果
背景 今天接到一个需求是,使用高斯模糊的效果对一个页面进行模糊处理,正好借这个机会来整理一下 css3 中高斯模糊的两个 API API介绍 filter 说明: 该 API 是一个过滤器,不仅能实现高斯模糊,还有很多比如颜色偏移、…...

科技大势怎么看 2023怎么干?
2023年,科技的走向依旧是世界各国的关注重点,各国在纷纷设立自己的科技战略目标外,还在潜心研究不同技术领域的科技趋势,试图通过科技占据国际竞争的制高点。 随着我国深入实施创新驱动发展战略,推动产业结构优化升级&…...

盘点曾经很火但消失了的8个软件
目录 1、飞信 3、暴风影音 4、千千静听 5、虾米音乐 6、快车下载 7、人人网 8、QQ农场 今天小编给大家分享曾经很火但消失了的8个软件,你都用过吗? 1、飞信 飞信是中国移动通信集团公司推出的一款短信、语音、视频通信应用程序。它于2007年推出&a…...
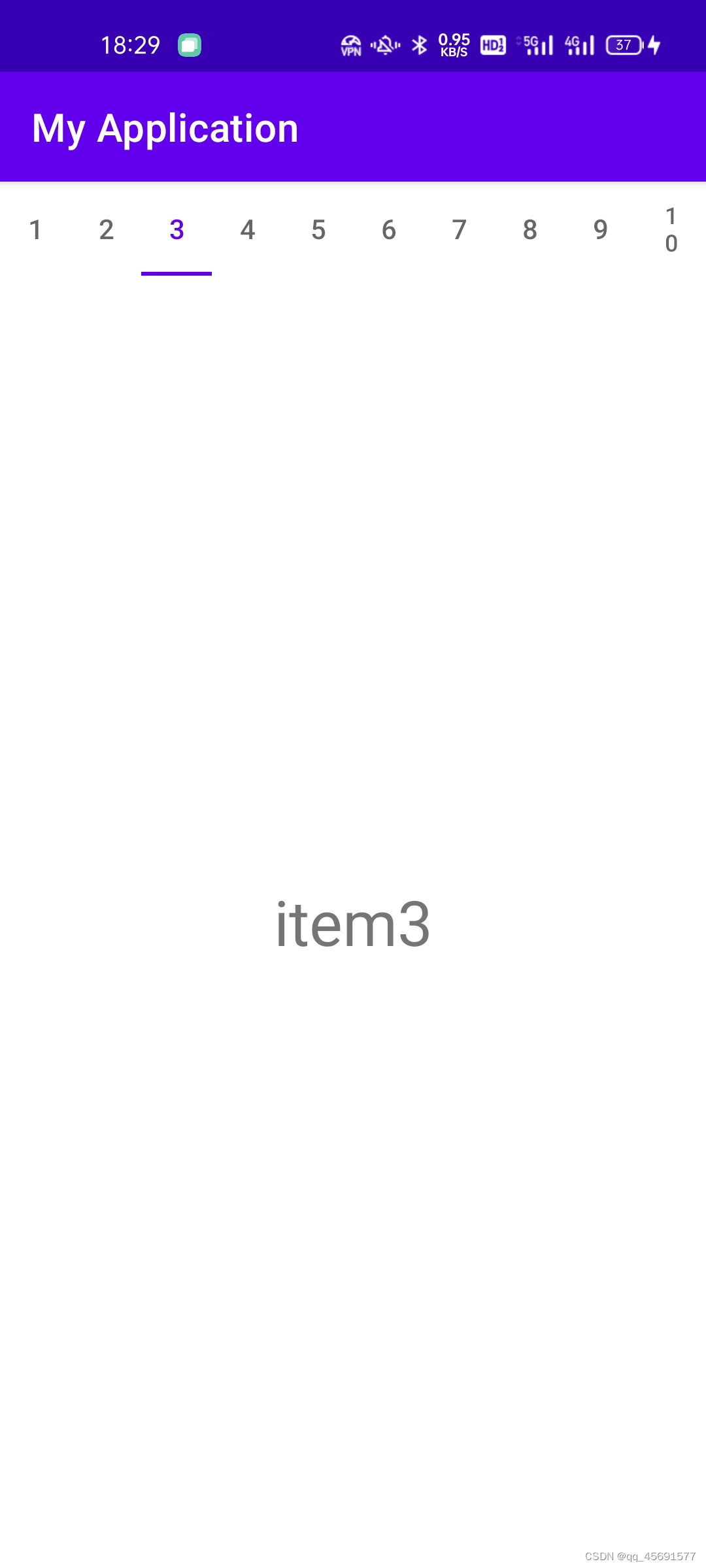
安卓 Frament + ViewPager使用示例
1. 组成架构 整个架构被包在一个外部Fragment之中,也可以放在一个Activity之中,随意。外部的fragment包含了两个组件,即途中的ViewPager和TabLayoutViewPager要套上一个FragmentStatePagerAdapter ,适配器负责new出一个个fragment…...
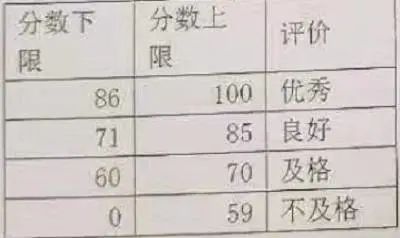
【银行测试】必看的四类题型:这可是最经典的一套题目了
目录:导读 一、根据题目要求写出具体LINUX操作命令 二、JMETER题目 三、根据题目要求写出具体SQL语句 四、测试案例设计题 金三银四面试面对大厂面试官提问,如何回答:花3天背完这100道软件测试面试题!银行测试的offer还不是手…...
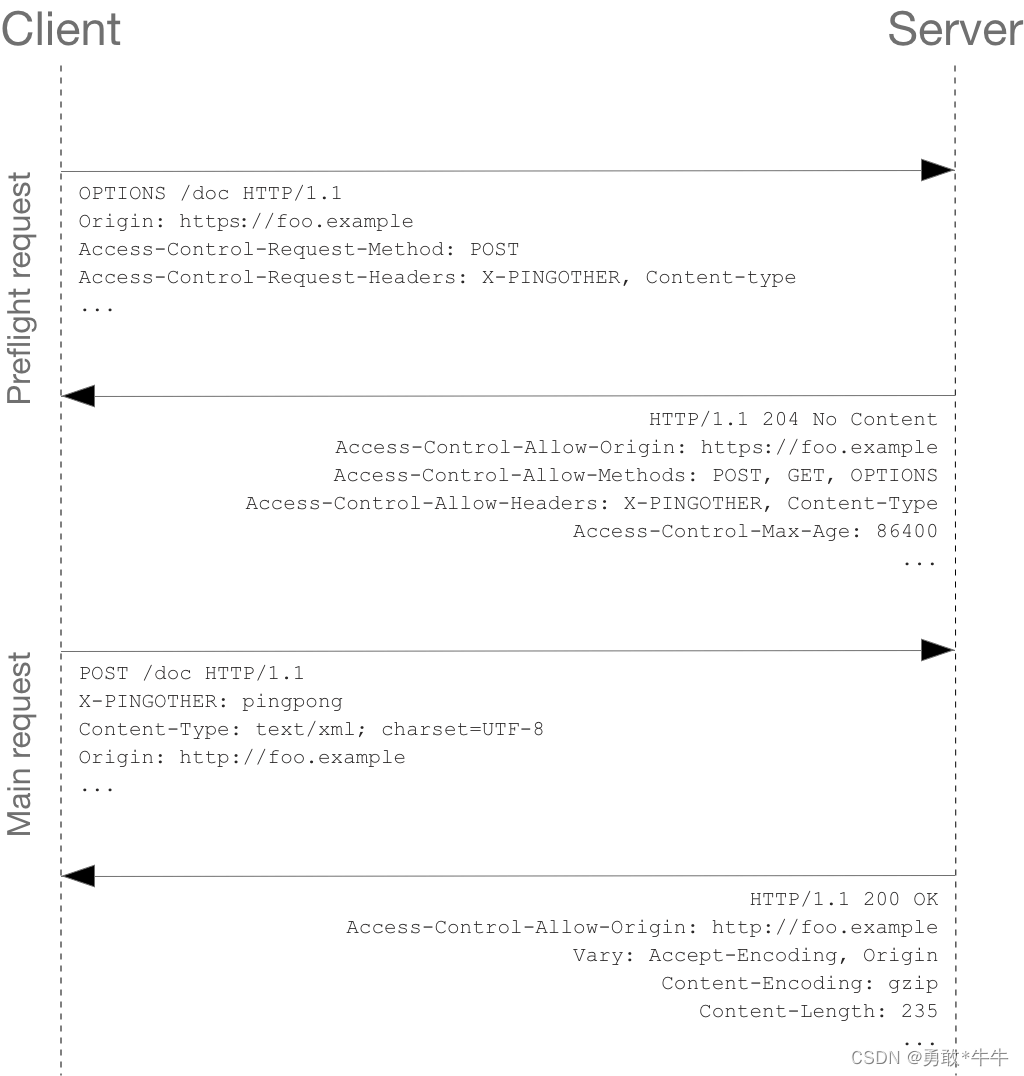
跨源资源共享(CORS)-亲测理解,以及对http的状态,参数的理解和使用,对预检请求的触发和解决
跨源资源共享(CORS)-亲测理解,以及对http的状态,参数的理解和使用 跨源资源共享(CORS,或通俗地译为跨域资源共享)是一种基于HTTP 头的机制,该机制通过允许服务器标示除了它自己以外的…...

学生使用的台灯该怎么选择?2023适合学生房间的灯推荐
随着社会的进步发展,我们的生活水平越来越高,很多家庭的孩子都开始使用台灯这种家居产品,对于学习任务繁重的他们来说,台灯确实可以起到保护眼睛、提高学习专注度的作用。那么不知道朋友们是否了解过,台灯该怎么选择呢…...
)
23种设计模式-桥接模式(安卓应用场景介绍)
概念 桥接模式是一种结构型设计模式,它通过将抽象与其实现分离来解耦。它使用接口(抽象类)作为桥梁,将一个抽象类与其实现类的代码分别独立开来,从而使它们可以各自独立地变化。桥接模式的核心思想是“组合优于继承”…...
 T3快速访问)
2021牛客OI赛前集训营-提高组(第四场) T3快速访问
2021牛客OI赛前集训营-提高组(第四场) 题目大意 有一棵n1n1n1个节点的树,根节点为0。给你一个kkk,定义集合Si{j∈Z∣max(1,i−k)≤j<i}∪{0}S_i\{j\in Z|\max(1,i-k)\leq j<i\}\cup\{0\}Si{j∈Z∣max(1,i−k)≤j<i…...
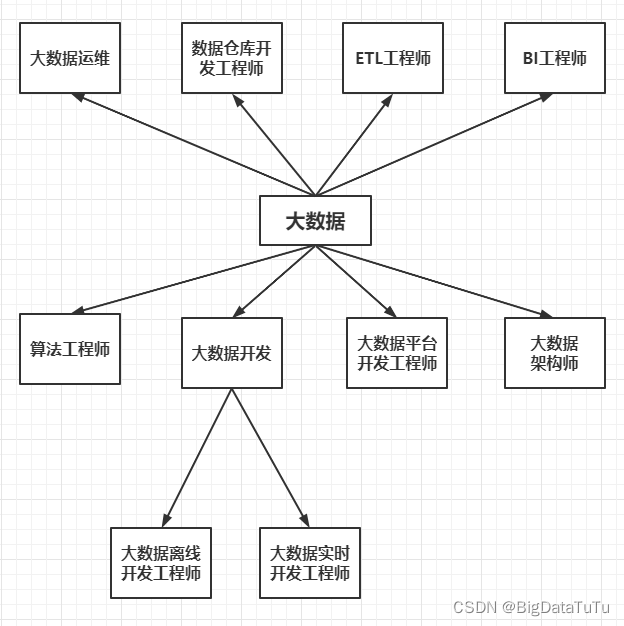
【大数据是什么】
大数据是什么大数据是做什么的?大数据主要有哪些职位 ?大数据运维工程师数据仓库开发工程师ETL工程师大数据开发工程师BI工程师算法工程师大数据平台开发工程师大数据架构师讲述一下自己的大数据学习之路大数据是做什么的? 2014年,…...
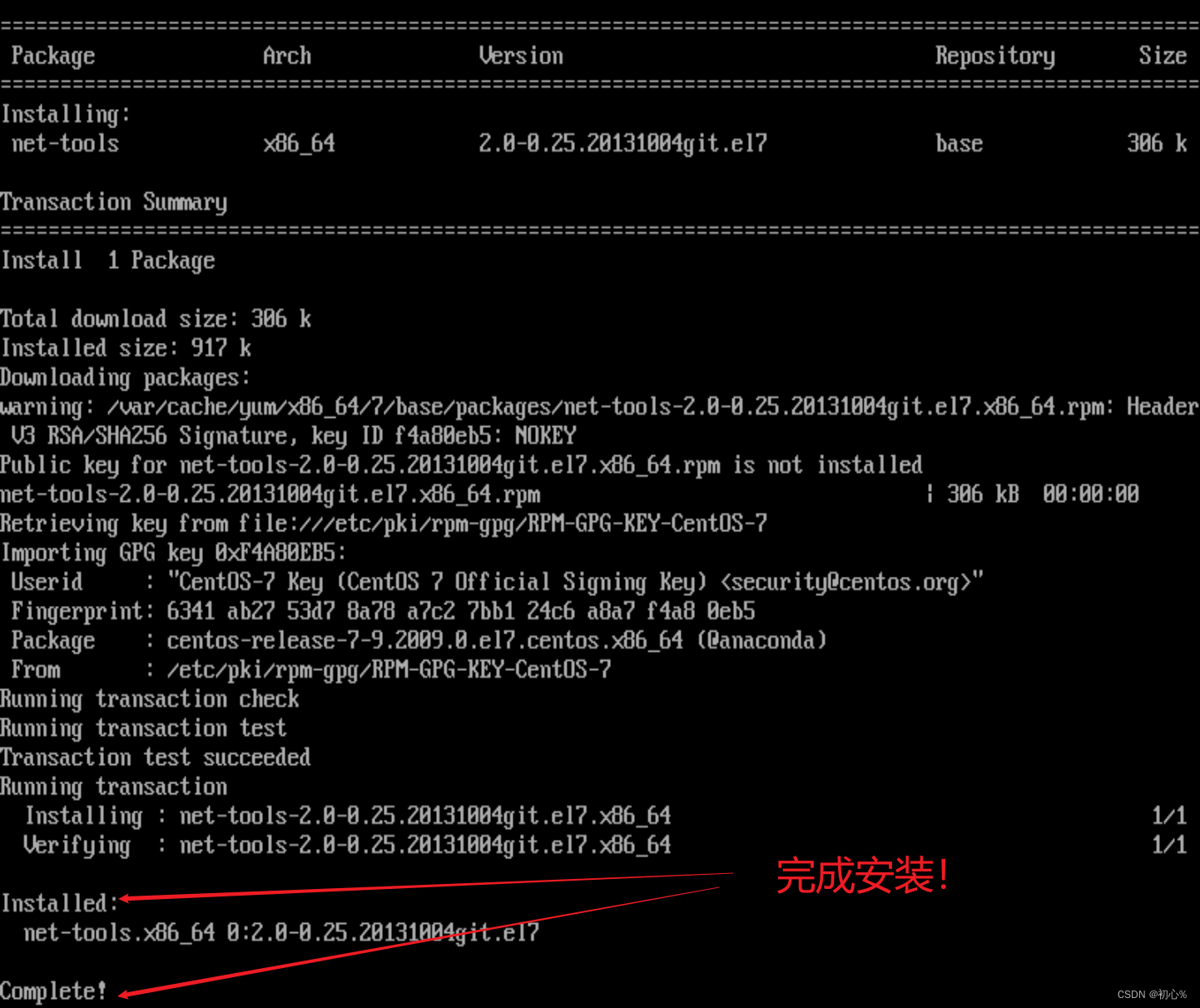
大数据 | centos7图形界面无法执行yum命令
大家好,今天是三八女神节了! 你知道吗?世界上第一位电脑程序设计师是名女性,Ada Lovelace (1815-1852)。 她是一位英国数学家兼作家,第一位主张计算机不只可以用来算数的人,也发表了第一段分析机用的演算…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
