C#算法之希尔排序
算法释义:希尔排序,也被称为缩小增量排序,是一种有效的排序算法,它是插入排序的一种更高效的改进版,通过比较一定间隔的元素来工作,然后逐步较少间隔来排序。
小编的理解啊,希尔排序的本质就是不断的分割、分割、再分割,直到间隔为1,这个时候,算法就与插入排序一致了。
希尔排序的优点:时间复杂度较小;属于原地排序,不需要额外的存储空间。
闲言少叙,上代码:
public static void sort(int[] arr) {int n = arr.length;int gap = n / 2; // 初始增量while (gap > 0) {for (int i = gap; i < n; i++) {int temp = arr[i];int j;// 对子序列进行插入排序for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {arr[j] = arr[j - gap];}arr[j] = temp;}gap /= 2; // 减少增量}}public static void main(String[] args) {int[] arr = {9, 8, 3, 7, 5, 2, 1, 6, 4};sort(arr);System.out.println("Sorted array: ");for (int i : arr) {System.out.print(i + " ");}}各位朋友,以上就是小编对希尔排序一点浅显的理解,希望给各位朋友一定的启发。
相关文章:

C#算法之希尔排序
算法释义:希尔排序,也被称为缩小增量排序,是一种有效的排序算法,它是插入排序的一种更高效的改进版,通过比较一定间隔的元素来工作,然后逐步较少间隔来排序。 小编的理解啊,希尔排序的本质就是不…...
)
校园餐厅预约系统(请打开git自行访问)
校园餐厅预约系统详细介绍 项目地址:https://gitee.com/zhang—xuan/online_booking_system 服务端部分 Socket类 作用:创建socket连接,作为服务端与客户端通信的基础。 Sock_Obj类 基类:定义了服务端需要的基本操作和属性。 派生…...
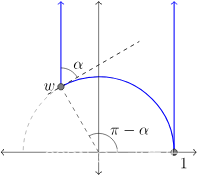
【双曲几何-05 庞加莱模型】庞加来上半平面模型的几何属性
文章目录 一、说明二、双曲几何的上半平面模型三、距离问题四、弧长微分五、面积问题 一、说明 庞加莱圆盘模型是表示双曲几何的一种方法,对于大多数用途来说它都非常适合几何作图。然而,另一种模型,称为上半平面模型,使一些计算变…...

Bookends for Mac:文献管理工具
Bookends for Mac,一款专为学术、研究和写作领域设计的文献管理工具,以其强大而高效的功能深受用户喜爱。这款软件支持多种文件格式,如PDF、DOC、RTF等,能够自动提取文献的关键信息,如作者、标题、出版社等,…...

SpringEL表达式编译模式SpelCompilerMode详解
目前网上没有搜到关于SpringEL表达式编译模式SpelCompilerMode的详细讲解,都是对官方文档的翻译,并没有详细说明根本差异。 该文章为个人原创,谢绝抄袭 SpringEL表达式官方文档:https://docs.spring.io/spring-framework/reference/core/expressions.html 在构建SpringE…...
物联网实战--平台篇之(一)架构设计
本项目的交流QQ群:701889554 物联网实战--入门篇https://blog.csdn.net/ypp240124016/category_12609773.html 物联网实战--驱动篇https://blog.csdn.net/ypp240124016/category_12631333.html 一、平台简介 物联网平台这个概念比较宽,大致可以分为两大类&#x…...

spi 驱动-数据发送流程分析
总结 核心函数是spi_sync, 设备驱动->核心函数-> 控制器驱动 实例分析 (gdb) c Continuing.Thread 115 hit Breakpoint 1, bcm2835_spi_transfer_one (master0xffffffc07b8e6000, spi0xffffffc07b911800, tfr0xffffff8009f53c40) at drivers/spi/spi-bcm2835…...
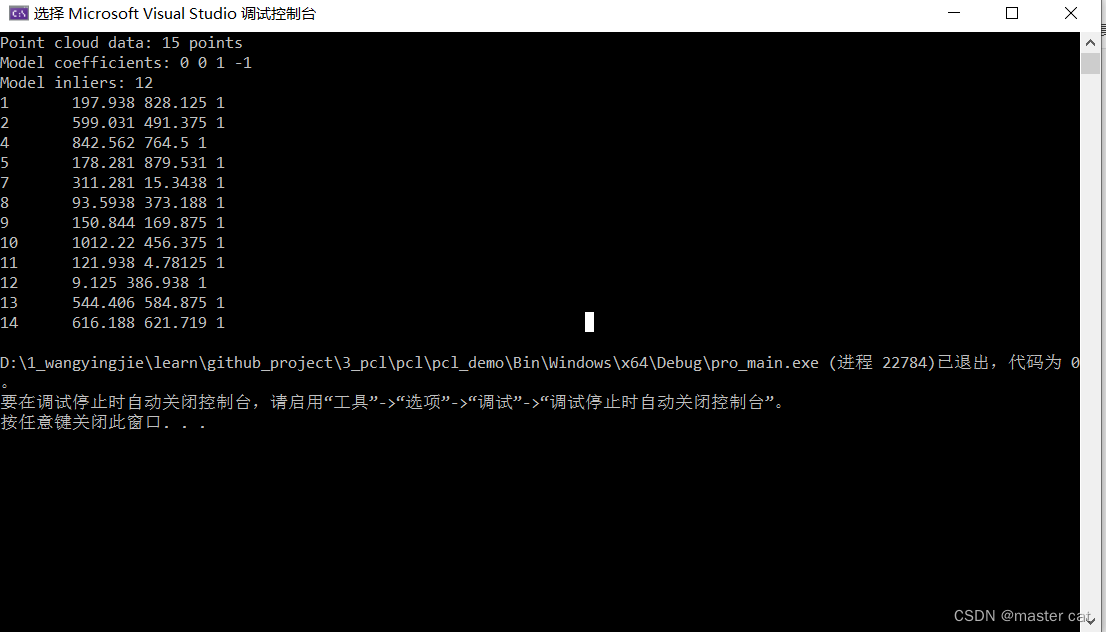
平面分割--------PCL
平面分割 bool PclTool::planeSegmentation(pcl::PointCloud<pcl::PointXYZ>::Ptr cloud, pcl::ModelCoefficients::Ptr coefficients, pcl::PointIndices::Ptr inliers) {std::cout << "Point cloud data: " << cloud->points.size() <<…...
前端之深拷贝
前提: 就是在实际开发中,我有一个编辑的弹窗,可以查看和编辑,因为弹窗里面是一个步骤条,点击下一步就要向对应的接口发送请求,考虑到就比如我点击下一步,此次表箱信息其实不需要修改࿰…...

2024年 Java 面试八股文——SpringCloud篇
目录 1.Spring Cloud Alibaba 中的 Nacos 是如何进行服务注册和发现的? 2.Spring Cloud Alibaba Sentinel 的流量控制规则有哪些? 3.Spring Cloud Alibaba 中如何实现分布式配置管理? 4.Spring Cloud Alibaba RocketMQ 的主要特点有哪些&…...

linux C语言Makefile
ChatGPT 在Linux中使用Makefile来自动化C语言项目的构建过程是很普遍的实践。Makefile是一个包含了一系列构建目标及如何构建这些目标的依赖和规则的文本文件。 一个基本的Makefile例子可能会像这样: # 定义编译器 CCgcc# 定义编译选项 CFLAGS-I.# 定义可执行文件…...
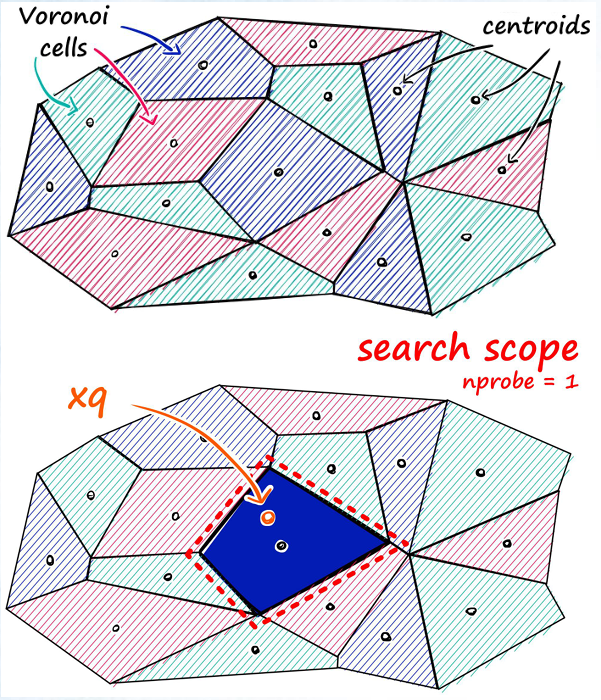
pgvector扩展在IvorySQL Oracle兼容模式下的应用实践
向量数据库是生成式人工智能(GenAI)的关键组成部分。作为PostgreSQL的重要扩展,pgvector支持高达16000维的向量计算能力,使得PostgreSQL能够直接转化为高效的向量数据库。 IvorySQL基于PostgreSQL开发,因此它同样支持添加pgvector扩展。在Ora…...

c++ 线程概述
C中的线程是并发编程的重要组成部分,它允许程序同时执行多个任务。以下是对C线程的概述: 基本概念: 并发:意味着两个或多个任务同时执行。在单核CPU上,由于只有一个CPU,某一时刻只能执行一个任务࿰…...

纯血鸿蒙APP实战开发——短视频切换实现案例
短视频切换实现案例 介绍 短视频切换在应用开发中是一种常见场景,上下滑动可以切换视频,十分方便。本模块基于Swiper组件和Video组件实现短视频切换功能。 效果图预览 使用说明 上下滑动可以切换视频。点击屏幕暂停视频,再次点击继续播放…...
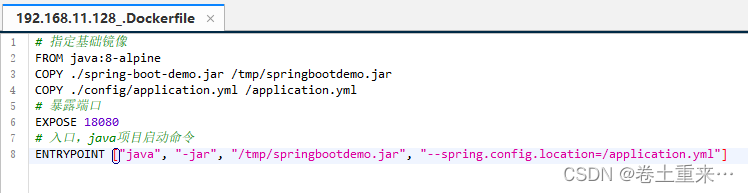
36.Docker-Dockerfile自定义镜像
镜像结构 镜像是将应用程序及其需要的系统函数库、环境、配置、依赖打包而成。 镜像是分层机构,每一层都是一个layer BaseImage层:包含基本的系统函数库、环境变量、文件系统 EntryPoint:入口,是镜像中应用启动的命令 其他:在…...

【webrtc】MessageHandler 4: 基于线程的消息处理:以Fake 收发包模拟为例
G:\CDN\rtcCli\m98\src\media\base\fake_network_interface.h// Fake NetworkInterface that sends/receives RTP/RTCP packets.虚假的网络接口,用于模拟发送包、接收包单纯仅是处理一个ST_RTP包 消息的id就是ST_RTP 类型,– 然后给到目的地:mediachannel处理: 最后消息消…...

C#运算符“/”使用方法
C#中,当需要对两个整数进行除法运算时,结果会被截断为整数部分,即使结果本应是一个小数。这是因为整数除法会丢弃小数部分,只保留整数部分。 要想保留小数部分,需要将至少其中一个操作数转换为float、double或者 deci…...
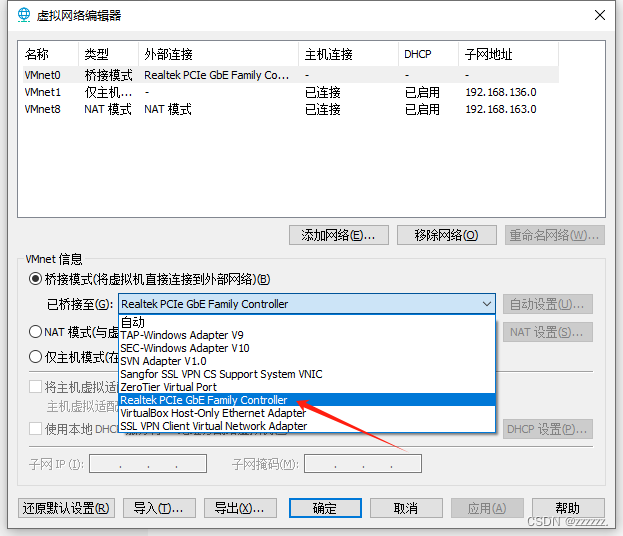
虚拟机网络桥接模式无法通信,获取到的ip为169.254.X.X
原因:VMware自动选择的网卡可能不对 解决:编辑-虚拟网络编辑器-更改桥接模式-选择宿主机物理网卡,断开虚拟机网络连接后重新连接即可...
【数据结构】初识数据结构
引入: 哈喽大家好,我是野生的编程萌新,首先感谢大家的观看。数据结构的学习者大多有这样的想法:数据结构很重要,一定要学好,但数据结构比较抽象,有些算法理解起来很困难,学的很累。我…...
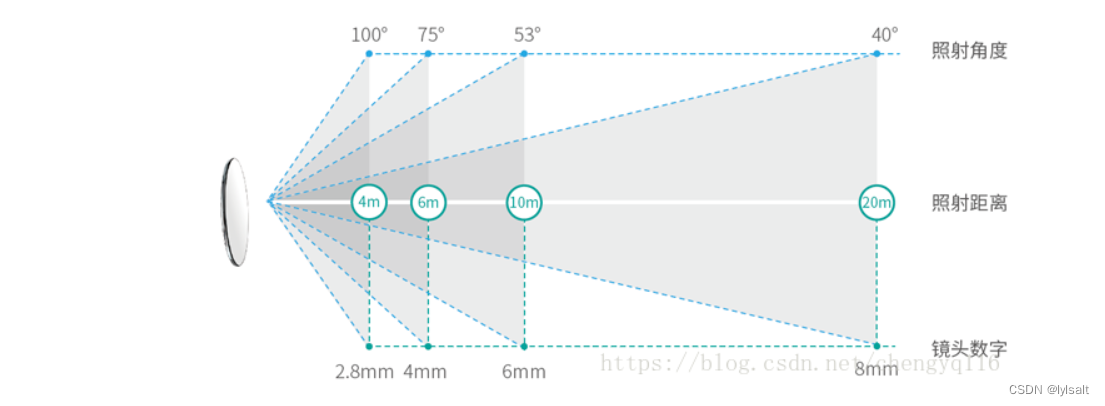
相机知识的补充
一:镜头 1.1MP的概念 相机中MP的意思是指百万像素。MP是mega pixel的缩写。mega意为一百万,mega pixel 指意为100万像素。“像素”是相机感光器件上的感光最小单位。就像是光学相机的感光胶片的银粒一样,记忆在数码相机的“胶片”ÿ…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...
