数据结构-二叉树-二叉搜索树
一、概念
二叉搜索树又称二叉排序树,它或者是一棵空树,或者具有以下性质的二叉树:
若它的左子树不为空,则左树上所有节点的值都小于根节点的值。
若它的右子树不为空,则右子树上所有节点的值都大于根节点的值。
它的左右子树也分别为二叉搜索树。最多找O(N)。
二、查找、插入、删除
插入
bool Insert(K& k)
{if (_root == nullptr){_root = new BSNode(k);return true;}BSNode* cur = _root;BSNode* parent = nullptr;while (cur){if (cur->_k < k){parent = cur;cur = cur->_right;}else if (cur->_k > k){parent = cur;cur = cur->_left;}}if (parent->_k < k){parent->_right = new BSNode(k);}else if (parent->_k > k){parent->_left = new BSNode(k);}else{return false;}return true;
}查找
bool Find(K k)
{BSNode* cur = _root;while (cur){if (cur->_k < k){cur = cur->_right;}else if (cur->_k > k){cur = cur->_left;}else{return true;}}return false;
}删除
依次删除7、14、3、8。7和14属于直接删除的场景
3、8属于需要替换法进行删除的场景。
1、没有孩子
2、一个孩字
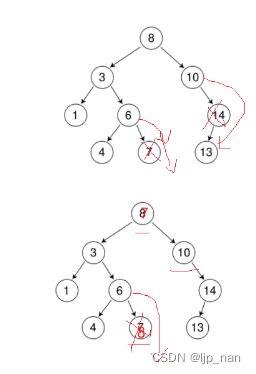
3、两个孩子,需要进行替换,也就是替换法,用左子树的最大节点或者右子树的最小节点。
最大节点为最右节点,最小节点就是最左节点 ,还需要处理要删除的节点为根节点,它没有左子树或者没有右子树的情况。

还有一种情况就是leftmax就是root的左子树的根,此时parent为nullptr所以我们需要让parent = cur
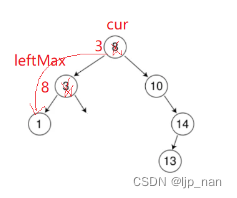
void Erase(K& k)
{BSNode* cur = _root;BSNode* parent = nullptr;while (cur){if (cur->_k < k){parent = cur;cur = cur->_right;}else if (cur->_k > k){parent = cur;cur = cur->_left;}else{//开始托孤//要删除的节点,左孩子为空if (cur->_left == nullptr){//需要判断删除节点就是根节点的情况if (cur == _root){_root = cur->_right;}else{if (parent->_right == cur){parent->_right = cur->_right;}else{parent->_left = cur->_right;}}}else if (cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else{if (parent->_right == cur){parent->_right = cur->_left;}else {parent->_left = cur->_left;}}}else //两个孩子的情况,就需要替代法来删除{//找到左子树中最大的节点BSNode* leftMax = cur->_left;//注意为什么这里等于cur;BSNode* parent = cur; while (leftMax->_right){parent = leftMax;leftMax = leftMax->_right;}//找到以后把删除节点和leftmax节点的值做交换std::swap(cur->_k, leftMax->_k);//我们该把父亲的那个孩子和cur节点的孩子连接起来呢需要判断if (parent->_left == leftMax){parent->_left = leftMax->_left;}else{parent->_right = leftMax->_left;}cur = leftMax;}delete cur;cur = nullptr;}}
}有序数组:二分查找,问题:插入删除效率不行
二叉搜索树:插入删除效率还行。
如果退化成下面的情况,插入删除的效率就变成了O(N),所以我们引出了AVL树红黑树B树系列。
接下来我们看一下递归版本的删除,插入和发现
bool _EraseR(BSNode*& root, const K& k)
{if (root == nullptr){return false;}if (root->_k < k){_EraseR(root->_right, k);}else if (root->_k > k){_EraseR(root->_left, k);}else{BSNode* del = root;if (root->_left == nullptr){root = root->_right;}else if (root->_right == nullptr){root = root->_left;}else{BSNode* leftMax = root->_left;while (leftMax->_right){leftMax = leftMax->_right;}std::swap(leftMax->_k, root->_k);return _EraseR(root->_left, k);}delete del;del = nullptr;return true;}
}
bool _InsertR(BSNode*& root,const K& k)
{if (root == nullptr){root = new BSNode(k);return true;}if (root->_k < k){_InsertR(root->_right, k);}else if (root->_k > k){_InsertR(root->_left, k);}else{return false;}
}
bool _FindR(BSNode* root, const K& k)
{if (root == nullptr)return false;BSNode* cur = root;if (cur->_k < k){_FindR(root->_right, k);}else if (cur->_k > k){_FindR(root->_left, k);}else{return true;}
}相关文章:

数据结构-二叉树-二叉搜索树
一、概念 二叉搜索树又称二叉排序树,它或者是一棵空树,或者具有以下性质的二叉树: 若它的左子树不为空,则左树上所有节点的值都小于根节点的值。 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值。 它…...

Linux 磁盘管理命令df du dd
文章目录 3.Linux 磁盘管理命令3.1 df:显示报告文件系统磁盘使用信息案例练习 3.2 du:显示目录或者文件所占的磁盘空间案例练习 3.3 dd:磁盘操作案例练习 3.Linux 磁盘管理命令 3.1 df:显示报告文件系统磁盘使用信息 作用&#x…...

Leetcode 3138. Minimum Length of Anagram Concatenation
Leetcode 3138. Minimum Length of Anagram Concatenation 1. 解题思路2. 代码实现 题目链接:3138. Minimum Length of Anagram Concatenation 1. 解题思路 这一题的话我们首先统计出来所有的字母出现的频率。 然后,我们只需要从头开始重新计数一下&…...
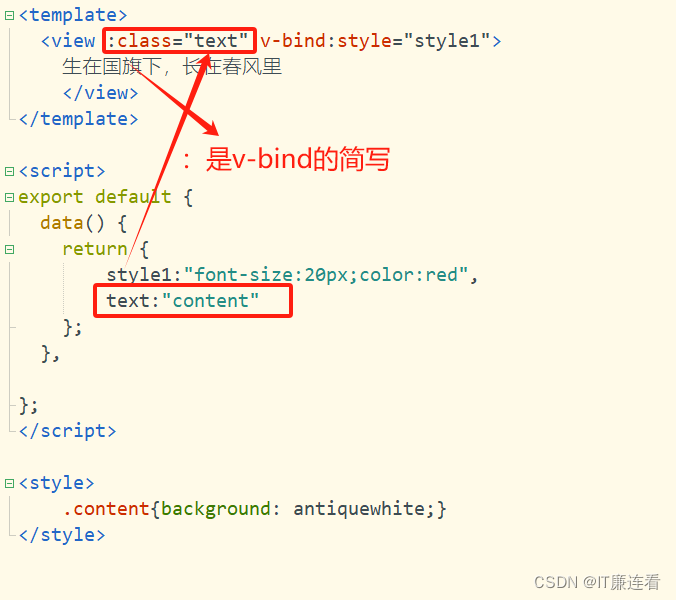
IT廉连看——UniApp——样式绑定
IT廉连看——UniApp——样式绑定 一、样式绑定 两种添加样式的方法: 1、第一种写法 写一个class属性,然后将css样式写在style中。 2、第二种写法 直接把style写在class后面 添加一些效果:字体大小 查看效果 证明这样添加样式是没有问题的…...

垃圾的flinkcdc
在 MySQL 中,创建表时使用反引号 将表名或字段名括起来的作用是: 保留字和关键字: 使用反引号可以避免使用MySQL的保留字和关键字作为表名或字段名时产生的冲突。比如,你可以创建一个名为 select 或 order 的表: sqlCopy Code C…...

关于视频号小店,常见问题解答,开店做店各方面详解
大家好,我是电商笨笨熊 视频号小店作为今年风口,一个新推出的项目,凭借着自身流量加用户群体的优势吸引了不少的电商玩家。 但对于很多玩家来说,视频号小店完全是一个新的项目、新的领域,因此也会存在很多的疑问&…...
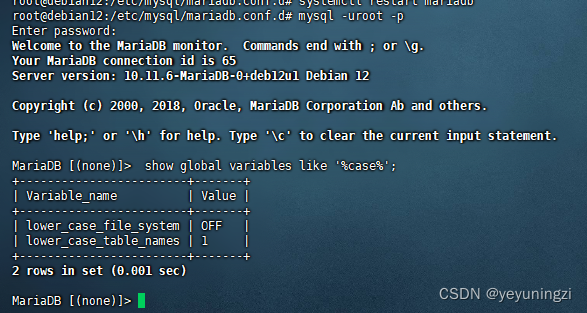
Debian mariadb 10.11设定表名 大小写不敏感方法
目录 问题表现:应用中查询 表提示 表不存在 处理步骤: 1、查询表名大小写敏感情况: show global variables like %case%; 2、修改mariadb 配置设置大小写 不敏感 mysql 配置大小写不敏感 mariadb 10.11设置表名大小写不敏感 /etc/mysq…...
常用六大加密软件排行榜|好用加密文件软件分享
为了保障数据安全,越来越多的企业开始使用文件加密软件。哪款加密软件适合企业哪些办公场景呢? 今天就给大家推荐一下文件加密软件排行榜的前六名: 1.域智盾 这款软件专为企业和政府机构设计,提供全面的文件保护解决方案。 点…...

百川2模型解读
简介 Baichuan 2是多语言大模型,目前开源了70亿和130亿参数规模的模型。在公开基准如MMLU、CMMLU、GSM8K和HumanEval上的评测,Baichuan 2达到或超过了其他同类开源模型,并在医学和法律等垂直领域表现优异。此外,官方还发布所有预…...
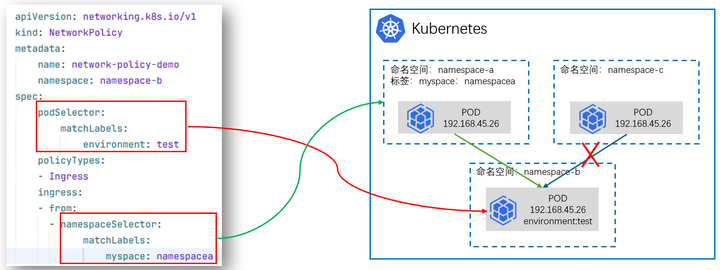
云原生专栏丨基于K8s集群网络策略的应用访问控制技术
在当今云计算时代,Kubernetes已经成为容器编排的事实标准,它为容器化应用提供了强大的自动化部署、扩展和管理能力。在Kubernetes集群中,网络策略(Network Policy)作为对Pod间通信进行控制的关键功能,对保障应用安全和隔离性起到了…...

MySQL 优化 - index_merge 导致查询偶发变慢
文章目录 前言问题描述原因分析总结 前言 今天遇到了一个有意思的问题,线上数据库 CPU 出现了偶发的抖动。定位到原因是一条查询语句偶发变慢造成的,随后通过调整表中的索引解决。 问题描述 下方是脱敏后的 SQL 语句: select oss_path f…...

SpringBoot自动连接数据库的解决方案
在一次学习设计模式的时候,沿用一个旧的boot项目,想着简单,就把数据库给关掉了,结果报错 Consider the following: If you want an embedded database (H2, HSQL or Derby), please put it on the classpath. 没有数据库的需…...

Docker-10 Docker Compose
一、前言 通过前面几篇文章的学习,我们可以通过Dockerfile文件让用户很方便的定义一个单独的应用容器。然而,在日常工作中,经常会碰到需要多个容器相互配合来完成某项任务的情况,或者开发一个Web应用,除了Web服务容器本身,还需要数据库服务容器、缓存容器,甚至还包括负…...

new mars3d.control.MapSplit({实现点击卷帘两侧添加不同图层弹出不同的popup
new mars3d.control.MapSplit({实现点击卷帘两侧添加不同图层弹出不同的popup效果: 左侧: 右侧: 说明:mars3d的3.7.12以上版本才支持该效果。 示例链接: 功能示例(Vue版) | Mars3D三维可视化平台 | 火星科技 相关代…...

数据库中虚拟表和临时表的区别?
虚拟表(Virtual Table)和临时表(Temporary Table)在数据库系统中都用于处理暂时性的数据存储需求,但它们的概念和用途有所不同: 虚拟表(通常是视图View): 虚拟表&#…...

Node.js -- mongoose
文章目录 1. 介绍2. mongoose 连接数据库3. 插入文件4. 字段类型5. 字段值验证6. 文档处理6.1 删除文档6.2 更新文档6.3 读取文档 7. 条件控制8. 个性化读取9. 代码模块化 1. 介绍 Mongoose是一个对象文档模型库,官网http://www.mongoosejs.net/ 方便使用代码操作mo…...
保持亮灯:监控工具如何确保 DevOps 中的高可用性
在快速发展的 DevOps 领域,保持高可用性 (HA) 至关重要。消费者期望应用程序具有全天候响应能力和可访问性。销售损失、客户愤怒和声誉受损都是停机的后果。为了使 DevOps 团队能够在问题升级为中断之前主动检测、排除故障并解决问题,监控工具成为这种情…...
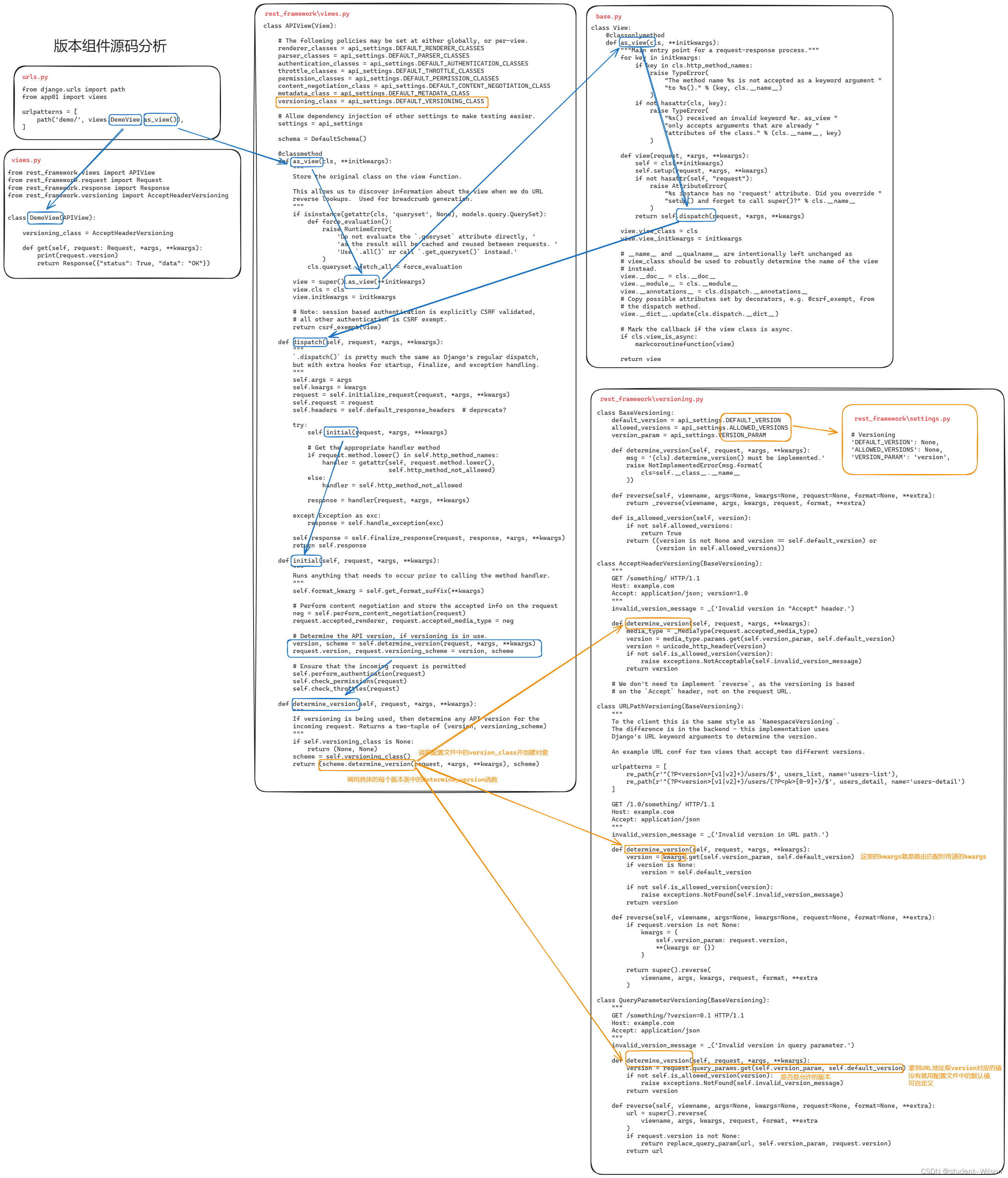
DRF版本组件源码分析
DRF版本组件源码分析 在restful规范中要去,后端的API中需要体现版本。 3.6.1 GET参数传递版本 from rest_framework.versioning import QueryParameterVersioning单视图应用 多视图应用 # settings.pyREST_FRAMEWORK {"VERSION_PARAM": "versi…...

C#算法之希尔排序
算法释义:希尔排序,也被称为缩小增量排序,是一种有效的排序算法,它是插入排序的一种更高效的改进版,通过比较一定间隔的元素来工作,然后逐步较少间隔来排序。 小编的理解啊,希尔排序的本质就是不…...
)
校园餐厅预约系统(请打开git自行访问)
校园餐厅预约系统详细介绍 项目地址:https://gitee.com/zhang—xuan/online_booking_system 服务端部分 Socket类 作用:创建socket连接,作为服务端与客户端通信的基础。 Sock_Obj类 基类:定义了服务端需要的基本操作和属性。 派生…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...
