数塔问题(蛮力算法和动态规划)
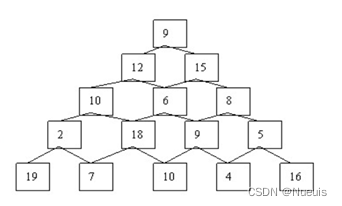
题目:如下图是一个数塔,从顶部出发在每一个节点可以选择向左或者向右走,一直走到底层,要求找出一条路径,使得路径上的数字之和最大,及路径情况。(使用蛮力算法和动态规划算法分别实现)
#include<bits/stdc++.h>
#define MAX_SIZE 100
using namespace std;
//蛮力算法
int maxPathSumForce(int pyramid[][MAX_SIZE],int row){if(row==1){return pyramid[0][0];}int maxSum=pyramid[0][0];for(int i=1;i<row;i++){for(int j=0;j<i;j++){if(j==0){pyramid[i][j]+=pyramid[i-1][j]; }else if(j==i){pyramid[i][j]+=pyramid[i-1][j-1];}else{pyramid[i][j] += (pyramid[i - 1][j - 1] > pyramid[i - 1][j] ? pyramid[i - 1][j - 1] : pyramid[i - 1][j]);}if (pyramid[i][j] > maxSum) {maxSum = pyramid[i][j];}
}}return maxSum;
} //动态规划算法int maxPathSumDP(int pyramid[][MAX_SIZE], int rows) {if (rows == 1) {return pyramid[0][0];}for (int i = rows - 2; i >= 0; i--) {for (int j = 0; j <= i; j++) {pyramid[i][j] += (pyramid[i + 1][j] > pyramid[i + 1][j + 1] ? pyramid[i + 1][j] : pyramid[i + 1][j + 1]);}}return pyramid[0][0];
}signed main()
{int pyramid[MAX_SIZE][MAX_SIZE];int row,num;cout<<"请输入数塔的层数:";cin>>row;cout<<"请输入数塔的数字(每层从左到右依次输入):"<<endl;for(int i=0;i<row;i++){for(int j=0;j<=i;j++){cin>>num;pyramid[i][j]=num;}}cout<<"蛮力算法最大路径和为:"<<maxPathSumForce(pyramid,row)<<endl;cout<<"动态规划算法最大路径和为:"<<maxPathSumDP(pyramid,row)<<endl; } 蛮力算法的解释:
1. 首先,如果金字塔只有一行(rows == 1),则直接返回金字塔顶部的值(pyramid[0][0])。
2. 初始化最大路径和为金字塔顶部的值(maxSum = pyramid[0][0])。
3. 使用两个嵌套的循环遍历金字塔的每一行和每一列。外层循环变量i表示行数,内层循环变量j表示列数。
4. 在内层循环中,根据当前位置的行数和列数,计算当前位置的值。具体计算方式如下:
- 如果当前位置是行的开头(j == 0),则当前位置的值等于上一行同列位置的值加上当前位置的值(pyramid[i][j] += pyramid[i - 1][j])。
- 如果当前位置是行的末尾(j == i),则当前位置的值等于上一行前一列位置的值加上当前位置的值(pyramid[i][j] += pyramid[i - 1][j - 1])。
- 否则,当前位置的值等于上一行前一列位置的值和上一行同列位置的值中的较大值(pyramid[i][j] += (pyramid[i - 1][j - 1] > pyramid[i - 1][j] ? pyramid[i - 1][j - 1] : pyramid[i - 1][j]))。
5. 在内层循环中,每次更新当前位置的值后,判断当前位置的值是否大于最大路径和(maxSum)。如果是,则更新最大路径和为当前位置的值。
动态规划算法的解释:(从下到上代码更加简洁,可能性更小)
1. 首先,如果金字塔只有一行(rows == 1),则直接返回金字塔顶部的值(pyramid[0][0])。
2. 使用两个嵌套的循环从倒数第二行开始向上遍历金字塔的每一行和每一列。外层循环变量i表示行数,内层循环变量j表示列数。
3. 在内层循环中,根据当前位置的行数和列数,计算当前位置的值。具体计算方式如下:
- 当前位置的值等于当前位置的值加上 下一行同列位置和下一行下一列位置中的较大值(pyramid[i][j] += (pyramid[i + 1][j] > pyramid[i + 1][j + 1] ? pyramid[i + 1][j] : pyramid[i + 1][j + 1]))。
4. 循环结束后,金字塔顶部的值即为从顶部到底部的最大路径和。
5. 返回金字塔顶部的值。
相关文章:

数塔问题(蛮力算法和动态规划)
题目:如下图是一个数塔,从顶部出发在每一个节点可以选择向左或者向右走,一直走到底层,要求找出一条路径,使得路径上的数字之和最大,及路径情况。(使用蛮力算法和动态规划算法分别实现) #include…...

启动 Redis 服务和连接到 Redis 服务器
启动 Redis 服务和连接到 Redis 服务器的步骤通常依赖于你的操作系统和 Redis 的安装方式。以下是一些常见的步骤: ### 启动 Redis 服务 对于大多数 Linux 发行版,Redis 服务可以通过以下命令启动: 1. 如果 Redis 是通过包管理器安装的&am…...
我独自升级崛起在哪下载 我独自升级电脑PC端下载教程分享
将于5月8日在全球舞台闪亮登场的动作角色扮演游戏《我独自升级崛起》,灵感源自同名热门动画与网络漫画,承诺为充满激情的游戏玩家群体带来一场集深度探索与广阔体验于一身的奇幻旅程。该游戏以独特的网络武侠世界观为基底,展现了一位普通人踏…...

STM32F4xx开发学习—GPIO
GPIO 学习使用STM32F407VET6GPIO外设 寄存器和标准外设库 1. 寄存器 存储器映射 存储器本身是不具有地址的,是一块具有特定功能的内存单元,它的地址是由芯片厂商或用户分配,给存储器分配地址的过程就叫做存储区映射。给内存单元分配地址之后…...

引领农业新质生产力,鸿道(Intewell®)操作系统助力农业机器人创新发展
4月27日至29日,2024耒耜国际会议在江苏大学召开。科东软件作为特邀嘉宾出席此次盛会,并为江苏大学-科东软件“农业机器人操作系统”联合实验室揭牌。 校企联合实验室揭牌 在开幕式上,江苏大学、科东软件、上交碳中和动力研究院、遨博智能研究…...
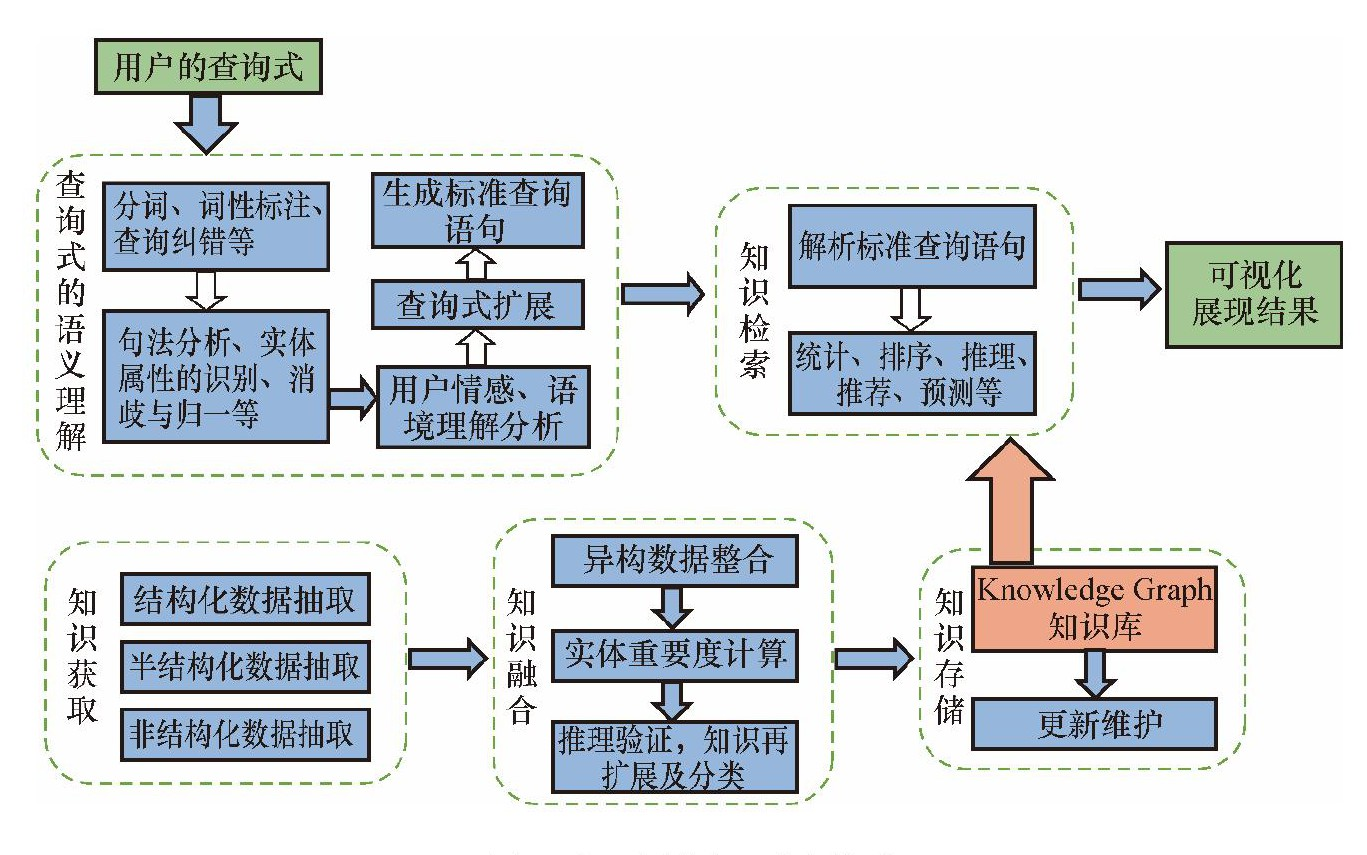
扩展学习|一文读懂知识图谱
一、知识图谱的技术实现流程及相关应用 文献来源:曹倩,赵一鸣.知识图谱的技术实现流程及相关应用[J].情报理论与实践,2015, 38(12):127-132. (一)知识图谱的特征及功能 知识图谱是为了适应新的网络信息环境而产生的一种语义知识组织和服务的方…...
ubuntu中的docker记录(3)——如何安装nvidia-docker以更好地支持GPU加速计算应用程序的运行
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、nvidia-docker2的安装1. 安装docker2. 安装nvidia-docker2(1) 添加密钥(2) 更新软件列表(3) 安装nvidia-docker2(4) 测试nvidia-docker2 二、可能的报错及解…...

MLP实现fashion_mnist数据集分类(1)-模型构建、训练、保存与加载(tensorflow)
1、查看tensorflow版本 import tensorflow as tfprint(Tensorflow Version:{}.format(tf.__version__)) print(tf.config.list_physical_devices())2、fashion_mnist数据集下载与展示 (train_image,train_label),(test_image,test_label) tf.keras.datasets.fashion_mnist.l…...

ChatGPT-税收支持新质生产力
Prompt: 税收发展助力新质生产力 Response: 是的,税收发展可以促进新质生产力的发展。通过税收政策的调整和优化,政府可以提供更好的创新环境,激发企业投资研发,推动新技术、新产品的出现,从而推动经济结构升级和新…...

Linux下深度学习虚拟环境的搭建与模型训练
在深度学习实践中,环境配置是十分重要且免不了的一步。本文以 YOLOv4 模型,介绍在Linux下虚拟环境配置到模型训练的过程。 安装Miniconda: Miniconda是Anaconda的一个轻量级版本,非常适合用于科学计算和数据处理。 wget https:…...

Map-Reduce是个什么东东?
MapReduce是一种用于使用并行分布式算法在集群计算机上处理大型数据集的编程模型及其相关实现。这一概念首先由Google普及,并随后作为Apache Hadoop项目的一部分开源发布。 MapReduce的基本工作流程: 映射(Mapping):这是第一阶段,…...

上位机工作感想-从C#到Qt的转变-2
2.技术总结 语言方面 最大收获就是掌握了C Qt编程,自己也是粗看了一遍《深入理解计算机系统》,大致了解了计算机基本组成、虚拟内存、缓存命中率等基基础知识,那本书确实有的部分看起来很吃力,等这段时间忙完再研读一遍。对于封装…...
)
【C++】C++ 中 的 lambda 表达式(匿名函数)
C11 引入的匿名函数,通常被称为 Lambda 函数,是语言的一个重要增强,它允许程序员在运行时创建简洁的、一次性使用的函数对象。Lambda 函数的主要特点是它们没有名称,但可以捕获周围作用域中的变量,这使得它们非常适合在…...
OpenSSL实现AES-CBC加解密,可一次性加解密任意长度的明文字符串或字节流(QT C++环境)
本篇博文讲述如何在Qt C的环境中使用OpenSSL实现AES-CBC-Pkcs7加/解密,可以一次性加解密一个任意长度的明文字符串或者字节流,但不适合分段读取加解密的(例如,一个4GB的大型文件需要加解密,要分段读取,每次…...

cURL:命令行下的网络工具
序言 在当今互联网时代,我们经常需要与远程服务器通信,获取数据、发送请求或下载文件。在这些情况下,cURL 是一个强大而灵活的工具,它允许我们通过命令行进行各种类型的网络交互。本文将深入探讨 cURL 的基本用法以及一些高级功能…...
)
Baumer工业相机堡盟工业相机如何通过NEOAPISDK查询和轮询相机设备事件函数(C#)
Baumer工业相机堡盟工业相机如何通过NEOAPISDK查询和轮询相机设备事件函数(C#) Baumer工业相机Baumer工业相机NEOAPI SDK和相机设备事件的技术背景Baumer工业相机通过NEOAPISDK在相机中查询和轮询相机设备事件函数功能1.引用合适的类文件2.通过NEOAPISDK…...
、322. 零钱兑换、279.完全平方数、139.单词拆分)
Day45代码随想录动态规划part07:70. 爬楼梯(进阶版)、322. 零钱兑换、279.完全平方数、139.单词拆分
Day45 动态规划part07 完全背包 70. 爬楼梯(进阶版) 卡码网链接:57. 爬楼梯(第八期模拟笔试) (kamacoder.com) 题意:假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬至多m (1 < m < n)个…...

土壤重金属含量分布、Cd镉含量、Cr、Pb、Cu、Zn、As和Hg、土壤采样点、土壤类型分布
土壤是人类赖以生存和发展的重要资源之一,也是陆地生态系统重要的组成部分。近年来, 随着我国城市化进程加快,矿产资源开发、金属加工冶炼、化工生产、污水灌溉以及不合理的化肥农药施用等因素导致重金属在农田土壤中不断富集。重金属作为土壤环境中一种具有潜在危害…...
)
力扣:100284. 有效单词(Java)
目录 题目描述:输入:输出:代码实现: 题目描述: 有效单词 需要满足以下几个条件: 至少 包含 3 个字符。 由数字 0-9 和英文大小写字母组成。(不必包含所有这类字符。) 至少 包含一个 …...
如何快速掌握DDT数据驱动测试?
前言 网盗概念相同的测试脚本使用不同的测试数据来执行,测试数据和测试行为完全分离, 这样的测试脚本设计模式称为数据驱动。(网盗结束)当我们测试某个网站的登录功能时,我们往往会使用不同的用户名和密码来验证登录模块对系统的影响&#x…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...
