算法学习:二分查找

🔥 引言
在现代计算机科学与软件工程的实践中,高效数据检索是众多应用程序的核心需求之一。二分查找算法,作为解决有序序列查询问题的高效策略,凭借其对数时间复杂度的优越性能,占据着算法领域里举足轻重的地位。本篇内容旨在全面剖析二分查找算法的内在机制、实施步骤、性能特点及其在实际应用中的考量,为深入理解和有效应用此算法提供坚实的基础。📚
🌐 基础概念入门
什么是二分查找❓
想象一下,你站在一列整齐排列的书架前,想要找到某本书。
传统的做法是从头开始一本本地找,但如果你知道书架上的书是按字母顺序排列的,聪明的做法是直接走到中间,如果目标书在中间就找到了,不在的话根据书名比较判断是在左边还是右边的书架继续寻找。这就是二分查找的基本思想。🔍
如何工作❓
- 有序数组:二分查找的前提是数组必须是有序的,无论是升序还是降序。
- 分而治之:算法每次都将搜索区间缩小一半,通过比较中间元素来决定是在左半部分还是右半部分继续查找。
- 递归或迭代:二分查找可以递归或迭代实现,选择哪种方式取决于个人偏好和具体应用场景。
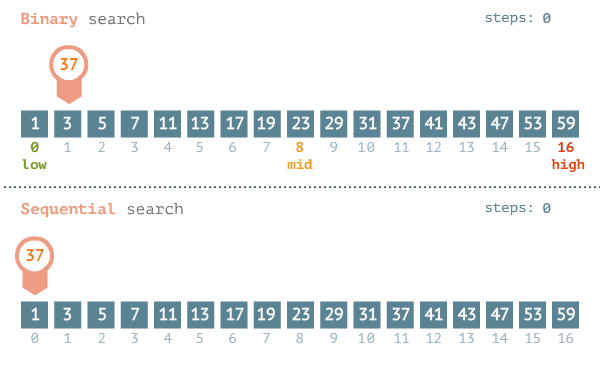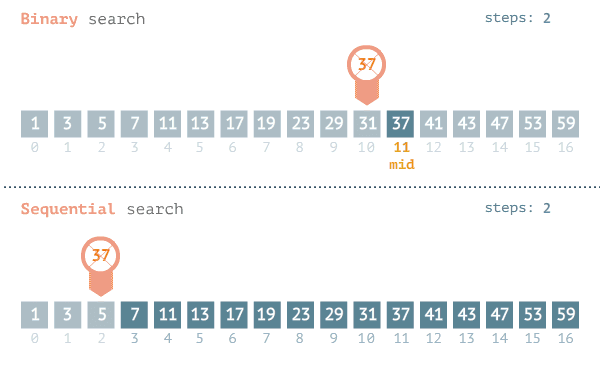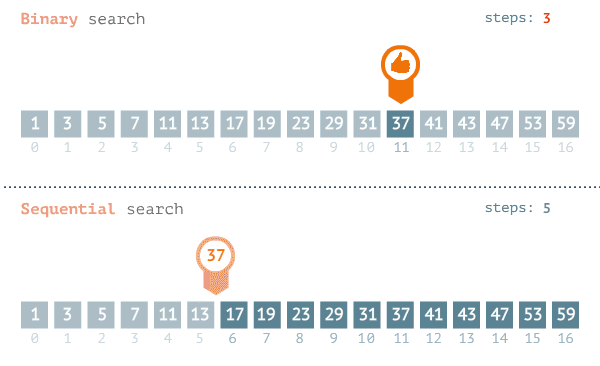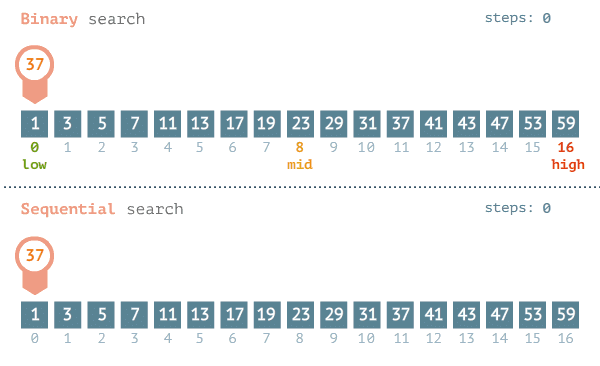
工作示例:
下面的示例说明了二分查找的工作原理。我随便想一个 1~100 的数字。你的目标是以最少的次数猜到这个数字。你每次猜测后,我会说小了、大了或对了。假设你从 1 开始依次往上猜,猜测过程会是这样。
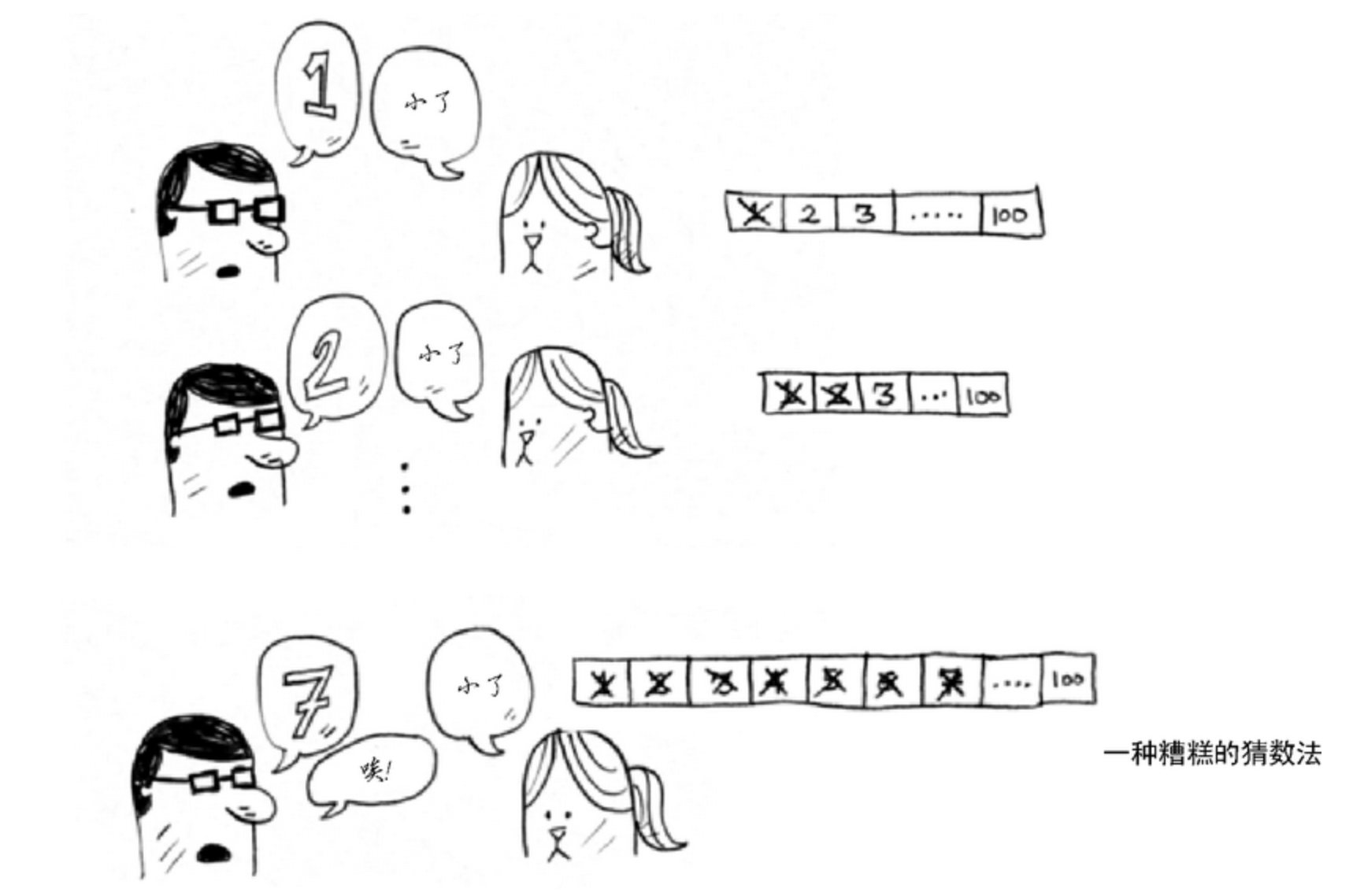
这是 简单查找,更准确的说法是傻找。每次猜测都只能排除一个数字,在最糟糕的情况下需要100次才能够找到这个数字。
而二分查找直接从有序列表的中间开始,一次就将排除一半的数字:
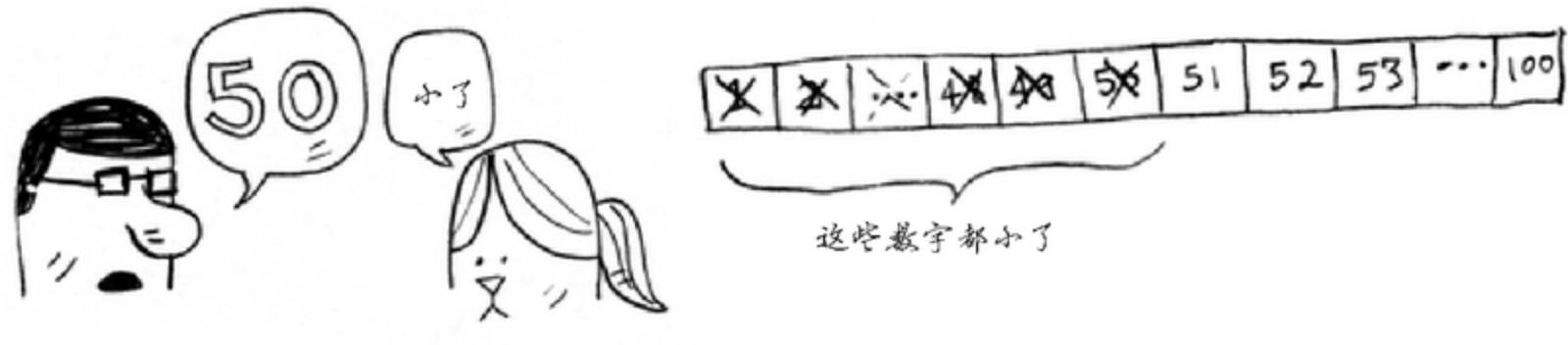
随后再从剩下的数字(50-100)的中间数(75)进行判断,又将排除掉一半的数字:
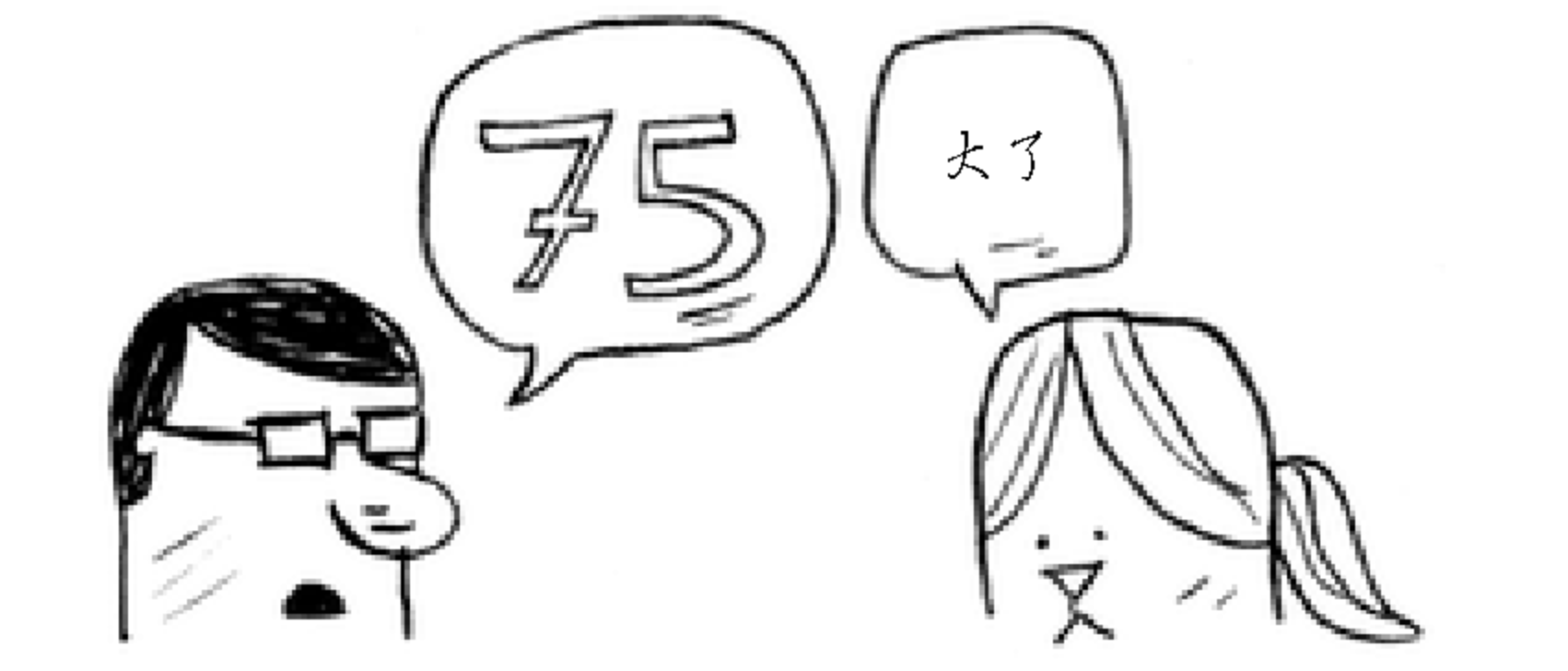
随后再从数字(50-75)的中间数进行判断,以此类推:找到最后的数:
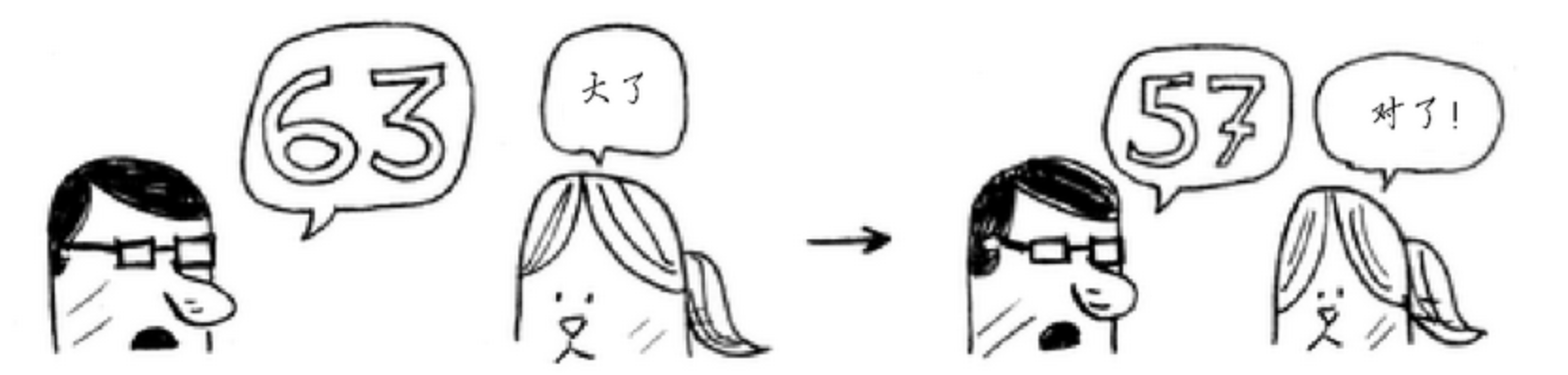
也就是说,100个元素的情况,使用二分查找最糟糕的情况也只需要7步就可以查找到相应的数字,比简单查找要少多了!
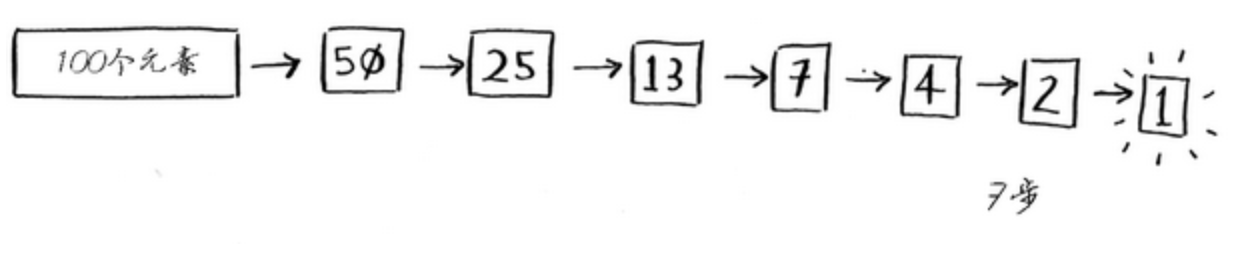
上述示例来自 力扣——算法图解
🔍 算法步骤详述
-
初始化指针:设置两个指针,
left初始为0,表示数组起始位置;right初始为数组最后一个元素的索引。 -
计算中间索引:为了避免整数溢出,通常采用
mid = left + (right - left) / 2。 -
比较并调整区间:
- 若
array[mid] == target,直接返回mid。 - 若
array[mid] < target,说明目标在右半部分,更新left = mid + 1。 - 若
array[mid] > target,则目标在左半部分,更新right = mid - 1。
- 若
-
重复步骤2和3,直到
left > right,此时说明数组中不存在目标值,返回-1或其他表示未找到的值。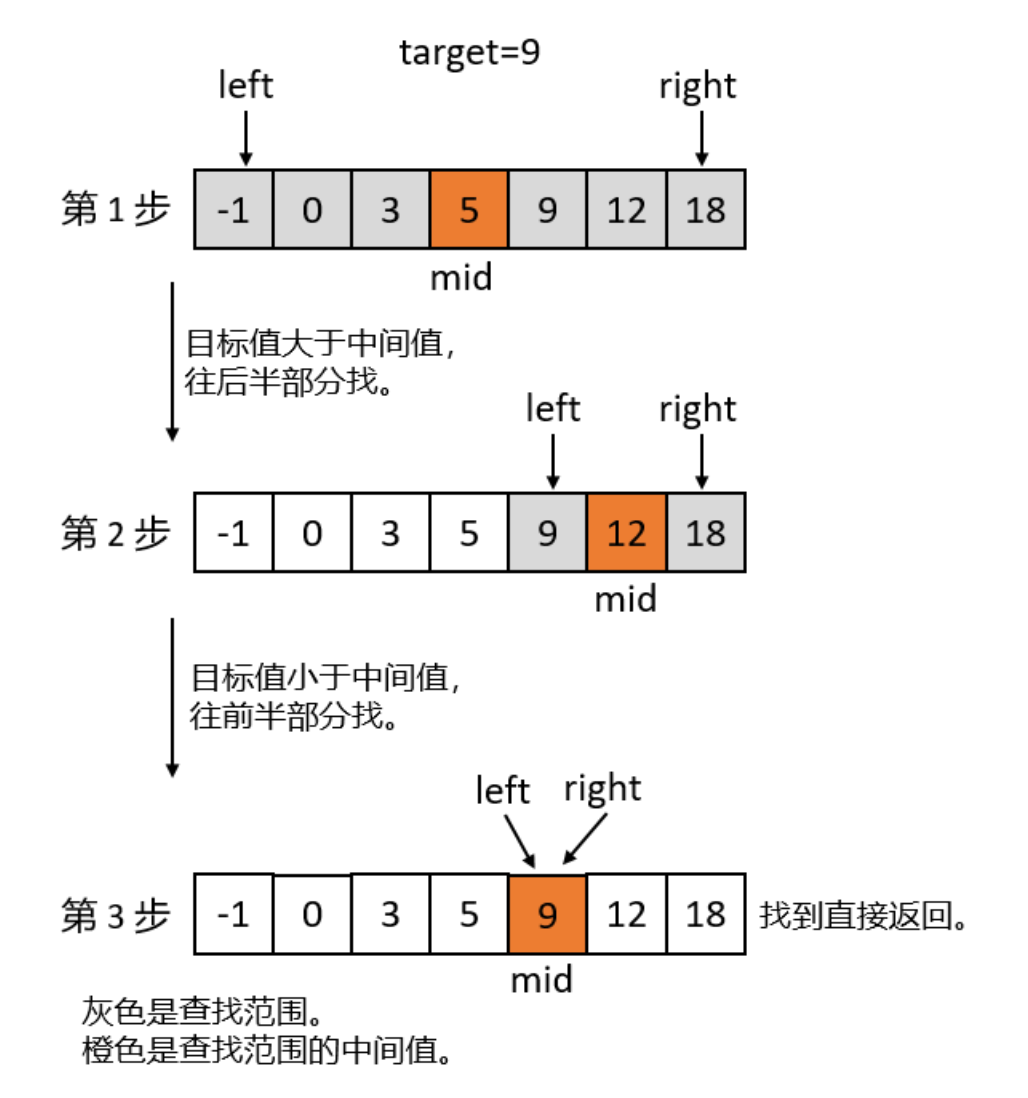
🧩 进阶理解
📌 大O表示法与时间复杂度分析
在深入探讨二分查找之前,了解大O表示法这一衡量算法效率的重要工具是不可或缺的。大O表示法用于描述算法在最坏情况下的时间复杂度,即随着输入数据量增长,算法执行时间增长的速度。它关注的是上界分析,帮助我们理解算法在大规模数据处理时的性能表现。
🍭 大O表示法简介
- 符号意义:“O”表示“Order of”,用来描述算法运行时间的增长率。
- 重点在于增速:它并不精确测量算法执行的确切时间,而是关注于当输入大小(通常用
n表示)增加时,算法执行时间增长的速率。 - 简化原则:忽略常数因子和低阶项,专注于最高阶项,因为当
n足够大时,这些因素对整体趋势影响不大。
大 O 表示法指出了算法有多快。例如,假设列表包含n个元素。简单查找需要检查每个元素,因此需要执行n次操作。使用大 O 表示法,这个运行时间为 𝑂(𝑛)。单位秒呢?没有——大 O 表示法指的并非以秒为单位的速度。大 O 表示法让你能够比较操作数,它指出了算法运行时间的增速。
🍭 二分查找的时间复杂度
对于二分查找算法,每次迭代都将搜索区间减半,这意味着查找次数与输入数据的对数成正比。因此,二分查找的时间复杂度为O(log n)。
🍭 与简单查找对比
为了更好地理解二分查找的效率,我们可以将其与简单(顺序/线性)查找进行对比:
-
简单查找(也称顺序/线性查找):在无序或有序列表中从头到尾遍历,直到找到目标值或遍历完整个列表。其时间复杂度为𝑂(𝑛),意味着随着数据量的增加,查找时间线性增长。
-
二分查找:在有序列表中通过不断缩小搜索范围来查找目标值。时间复杂度为𝑂(log 𝑛),表明当数据量翻倍时,所需查找步骤仅增加
log(𝑛)次,这是一种远低于线性增长的速度。
🍭 时间增速对比
-
简单查找的时间增速与数据量成正比,直观理解就是数据每增加一倍,查找时间大致也增加一倍。在大数据集上,这种增长速度很快变得不可承受。
-
二分查找的时间增速则要慢得多,因为它基于
对数函数。例如,即使数据量从1000增加到100万,二分查找所需的步骤只增加大约从10增加到20(基于2为底的对数),这种增长速率在处理大量数据时显得极为高效。
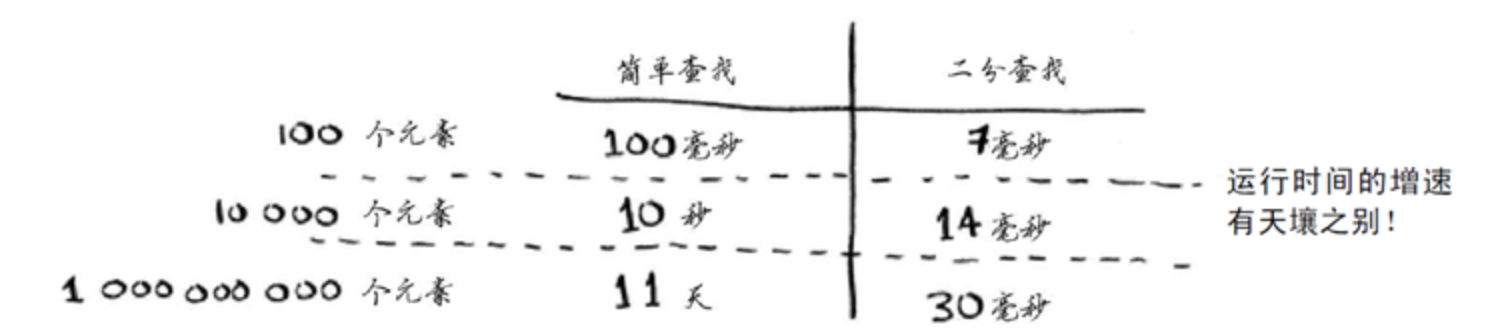
如图所示:假如查找100个元素使用简单查找需要100毫秒,使用二分查找需要7毫秒,可能这个差距可以让人接受。当数据增多时,查找1000000000个元素需要11天才可以查找完毕,而使用二分查找仅仅只需要30毫秒,比使用简单查找查询100个元素还要快的多!
简单查找(也称为顺序查找)的时间复杂度为𝑂(𝑛),这意味着如果数据量增加,查找所需的时间也会直接线性地增加:
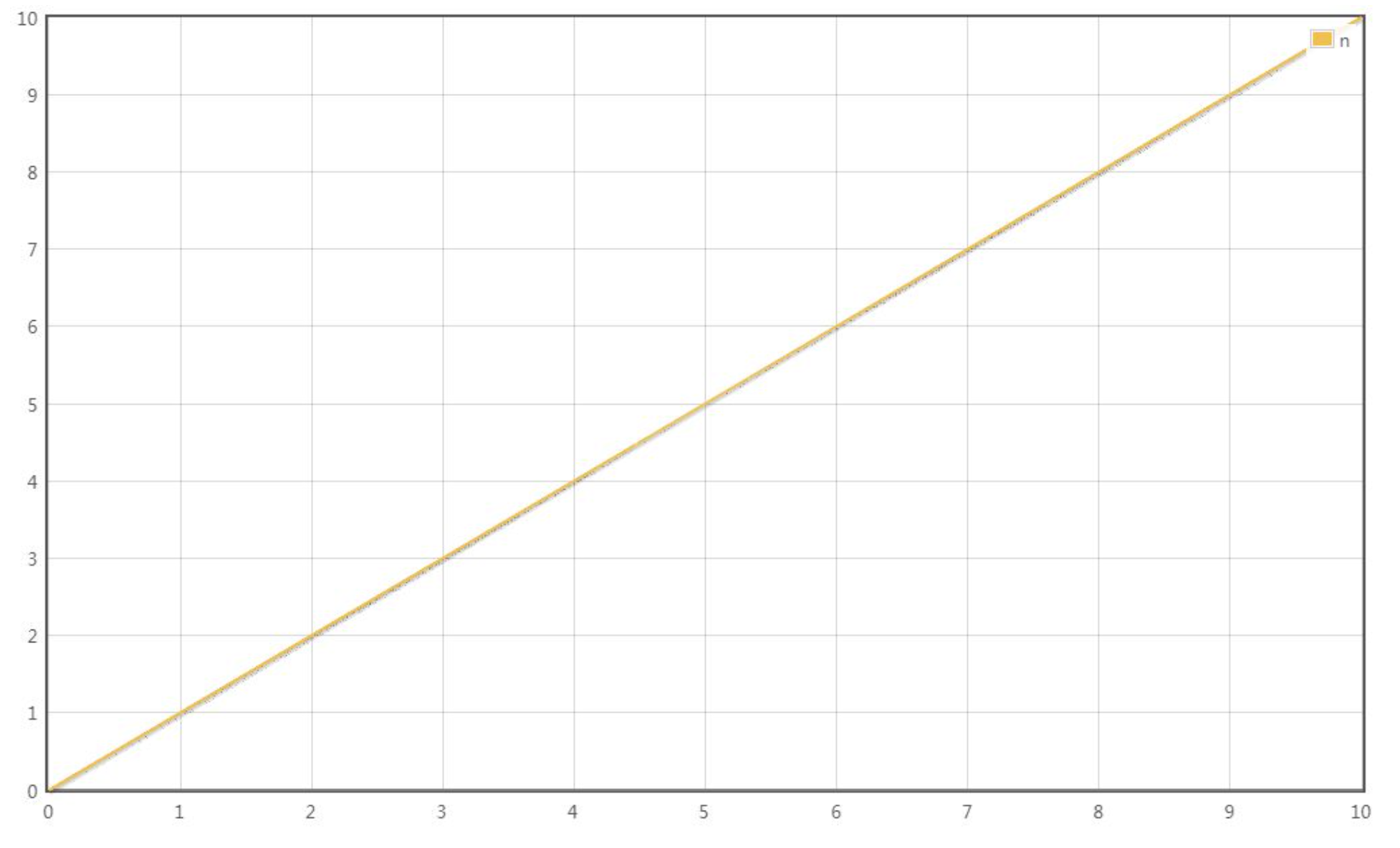
二分查找的时间复杂度为𝑂(log 𝑛),这意味着随着数据量n的增大,二分查找所需时间的增速远低于线性查找,它与数据量的对数成正比,而非与数据量本身成正比:
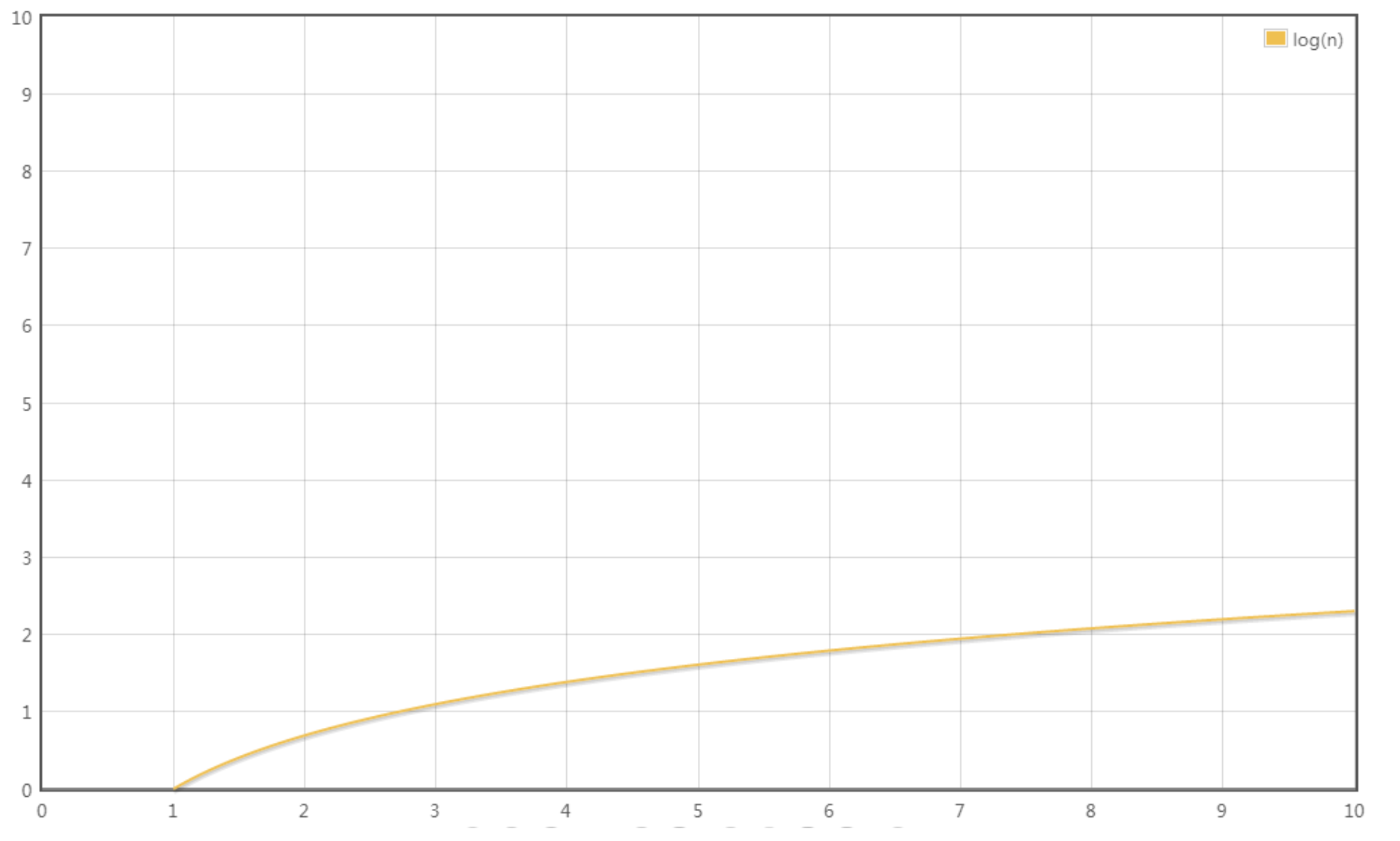
综上所述,二分查找由于其对数级的时间复杂度,在处理大规模有序数据集时,相比线性查找有着显著的性能优势,特别是在数据规模庞大的情况下,这种优势体现得更为明显。
📈 实践案例:JavaScript代码示例
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
/*** @param {number[]} nums // 传入一个有序的整型数组nums* @param {number} target // 需要查找的目标值target* @return {number} // 返回目标值在数组中的索引,如果未找到则返回-1*/
const search = function (nums, target) {let left = 0, right = nums.length - 1; // 初始化左右边界,left为数组起始索引,right为数组结束索引let result = -1; // 初始化结果变量result为-1,表示目标值未找到// 当左边界小于等于右边界时,继续循环while (left <= right) {let mid = left + Math.floor((right - left) / 2); // 计算中间索引mid,使用Math.floor向下取整保证mid为整数// 如果中间元素等于目标值if (nums[mid] === target) {result = mid; // 更新result为找到的目标值索引right = mid - 1; // 调整右边界继续在左半部分查找(若需查找重复值应调整此处逻辑)}// 如果中间元素小于目标值else if (nums[mid] < target) {left = mid + 1; // 缩小查找范围至右半部分,更新左边界}// 如果中间元素大于目标值else {right = mid - 1; // 缩小查找范围至左半部分,更新右边界}}return result; // 循环结束,返回最终查找结果
};// 示例使用
const sortedArray = [-1,0,3,5,9,12]; // 定义一个已排序的数组
console.log(search(sortedArray, 9)); // 在数组中查找数字9,并打印查找结果为 4
📌 总结
二分查找算法是针对有序数组高效查找特定元素的方法。其核心机制在于每次比较数组中间元素,根据比较结果将查找范围减半,直至找到目标或确定目标不存在。这一过程展现了𝑂(log 𝑛)的时间复杂度,意味着数据量每翻一倍,查找操作的次数只需增加一个固定比例(基于对数增长),而非线性增长。相比之下,线性查找的时间复杂度为𝑂(𝑛),数据量增长时效率下降明显。
大O表示法作为衡量算法效率的标准,帮助我们抽象理解算法随输入规模变化的性能表现,关注上界分析,忽略了常数项和低阶项,专注于影响最大的部分。在算法设计与分析中,它是评估和比较不同方案效率的有力工具。
总之,二分查找凭借其对数时间复杂度,在处理大规模有序数据时表现出色,是算法工具箱中不可或缺的高效利器。而对于任何算法的学习,理解大O表示法都是基础且关键的一步,它让我们能够科学地预测和优化程序的执行效率。
相关文章:

算法学习:二分查找
🔥 引言 在现代计算机科学与软件工程的实践中,高效数据检索是众多应用程序的核心需求之一。二分查找算法,作为解决有序序列查询问题的高效策略,凭借其对数时间复杂度的优越性能,占据着算法领域里举足轻重的地位。本篇内…...

github提交代码失败解决方案
1.打开github.push 工具 如果未安装github客户端请参考附录github 安装配置 2.设置Git的user name和email git config --global user.name "yourname" git config --global user.email "youremail" 3.生成SSH密钥 查看是否已经有了ssh密钥࿱…...
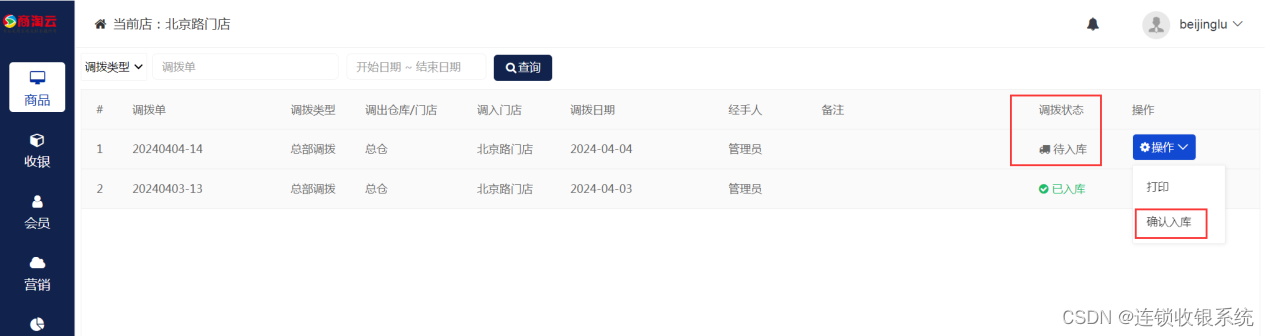
连锁收银系统总仓到门店库存调拨操作教程
1、进入系统后台,系统后台登录网址: 2、点击商品>门店调拨 3、选择调出仓库和调入门店 4、可选择添加商品逐个进行调拨,也可以批量导入需要调拨的商品 然后点击确定。 5、新增调拨后,系统会显示“待出库”状态 6、仓库已经准备…...
公网tcp转流
之前做过几次公网推流的尝试, 今天试了UDP推到公网, 再用TCP从公网拉下来, 发现不行, 就直接改用TCP转TCP了. 中间中转使用的python脚本, 感谢GPT提供技术支持: import socket import threadingdef tcp_receiver(port, forward_queue):"""接收TCP数据并将其放入…...
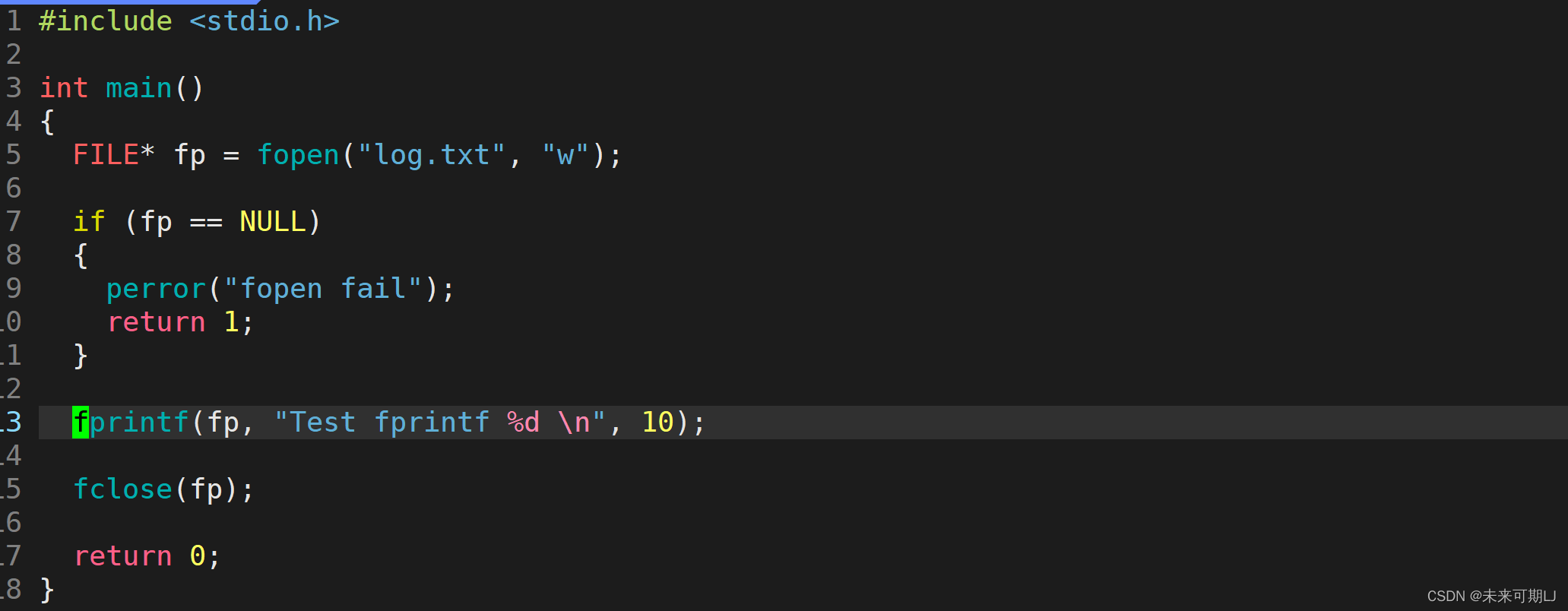
【Linux 基础 IO】文件系统
文章目录 1.初步理解文件2. fopen ( )的详解 1.初步理解文件 🐧① 打开文件: 本质是进程打开文件; 🐧②文件没有被打开的时候在哪里呢? ----- 在磁盘中; 🐧③进程可以打开很多个文件吗ÿ…...
Chrome浏览器安装React工具
一、如果网络能访问Google商店,直接安装官方插件即可 二、网络不能访问Google商店,使用安装包进行安装 1、下载react工具包 链接:https://pan.baidu.com/s/1qAeqxSafOiNV4CG3FVVtTQ 提取码:vgwj 2、chrome浏览器安装react工具…...

React常用组件分享
1、轮播组件: React Awesome Slider React Slider Carousel Component - react-awesome-slider...
JSON原生AJAX
文章目录 JSONFastjsonfastjson引入fastjson 常用APIfastjson作用常用API使用实例 ajax和json综合(重要)请求参数和响应数据都是普通字符串响应数据改为json格式请求和响应都是js数据封装到Result类和抽取到BaseController 原生AjaxAJAX的执行流程XMLHttpRequest对象使用原生的…...

Go图片列表
需求 在一个页面浏览目录下所有图片 代码 package mainimport ("net/http""fmt""io/ioutil""sort""strings""strconv""net/url" )func handleRequest(w http.ResponseWriter, r *http.Request) { de…...

1.4 初探JdbcTemplate操作
实战目的 掌握Spring框架中JdbcTemplate的使用,实现对数据库的基本操作。理解数据库连接池的工作原理及其在实际开发中的重要性。通过实际操作,加深对Spring框架中ORM(对象关系映射)的理解。 关键技术点 JdbcTemplate操作&…...
React 第二十一章 Portals
Portals 被翻译成传送门,是 React 库中的一个特性,它允许开发者将子组件渲染到父组件 DOM 层次结构之外的其他地方。 React 组件通常是在其父组件的 DOM 层次结构中渲染的,这意味着它们的输出会被插入到父组件的某个 DOM 元素中。然而&#…...

ADS基础教程9-理想模型和厂商模型实现及对比
目录 一、概要二、厂商库使用1.新建cell2.调用厂商库中元器件3.元器件替换及参数选择4.完成参数选择5.导入子图 三、仿真实现注意事项 一、概要 本文将介绍在ADS中调用厂商提供的库,来进行原理图仿真,并实现与ADS系统提供的理想元器件之间的比较。 二、…...
从零开始学AI绘画,万字Stable Diffusion终极教程(二)
【第2期】关键词 欢迎来到SD的终极教程,这是我们的第二节课 这套课程分为六节课,会系统性的介绍sd的全部功能,让你打下坚实牢靠的基础 1.SD入门 2.关键词 3.Lora模型 4.图生图 5.controlnet 6.知识补充 在第一节课里面,我们…...
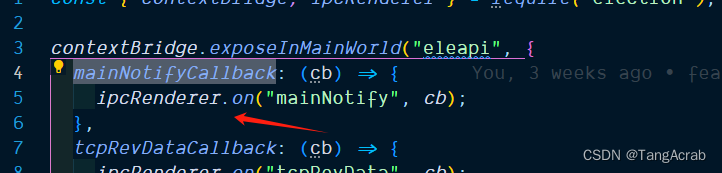
electron 通信总结
默认开启上下文隔离的情况下 渲染进程调用主进程方法: 主进程 在 main.js 中, 使用 ipcMain.handle,添加要处理的主进程方法 const { ipcMain } require("electron"); 在 electron 中创建 preload.ts 文件,从 ele…...
[基础] Unity Shader:顶点着色器(vert)函数
顶点着色器(Vertex Shader)是图形渲染的第一个阶段,它的输入来自于CPU。顶点着色器的处理单位是顶点,CPU输入进来的每个顶点都会调用一次顶点着色器函数,也就是我们在Shader代码里所定义的vert函数。本篇我们将会通过顶…...

什么是数据库的三大范式?
数据库的三大范式的目的是为了解决数据冗余的,提高数据的一致性和完整性,从而为了数据的性能和运维 第一范式: 就是数据的每一个列都是不可能分的,就是每一个表都包含一个实体的属性 第二范式: 就是在第一范式的基础上所有的非主键都必须完全依赖这个表的主键,而不是其他的主键…...
ASP.NET网上图书预约系统的设计
摘 要 《网上图书预约系统的设计》是以为读者提供便利为前提而开发的一个信息管理系统,它不仅要求建立数据的一致性和完整性,而且还需要应用程序功能的完备、易用等特点。系统主要采用VB.NET作为前端的应用开发工具,利用SQL Server2000数据…...

双色球案例【C#】
【实例类型】 1双色球类 方法的参数是对象。 public List<string> Numbers { get; set; } // 这个是对象的属性 /// <summary>/// 双色球类/// /// 作用:主要是用来封装数据/// </summary>public class DoubleChromosphere{//public str…...
【LeetCode刷题】739. 每日温度(单调栈)
1. 题目链接2. 题目描述3. 解题方法4. 代码 1. 题目链接 739. 每日温度 2. 题目描述 3. 解题方法 用一个栈st保存每个数的下标,同时创建一个数组res保存结果,初始值都为0。循环遍历题目中的数组temperature。如果temperature[i] > st.top()&#x…...

Docker-Consul容器服务更新与发现
前言 Docker Compose 则进一步简化了多个容器应用的编排与管理。另一方面,Consul 作为一款先进的服务发现工具,为分布式和微服务架构提供了可靠的服务注册与发现机制。本文将探讨 Docker Compose 和 Consul 在容器化环境中的协同作用,以及它…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

shell脚本质数判断
shell脚本质数判断 shell输入一个正整数,判断是否为质数(素数)shell求1-100内的质数shell求给定数组输出其中的质数 shell输入一个正整数,判断是否为质数(素数) 思路: 1:1 2:1 2 3:1 2 3 4:1 2 3 4 5:1 2 3 4 5-------> 3:2 4:2 3 5:2 3…...
