【中等】保研/考研408机试-动态规划1(01背包、完全背包、多重背包)
背包问题基本上都是模板题,重点:弄熟多重背包模板
dp[j]=max(dp[j-v[i]]+w[i],dp[j]) //核心思路代码(一维数组版)
dp[i][j]=max(dp[i-1][j], dp[i-1][j-v[i]]+w[i])//二维数字版
一、 0-1背包
一般输入两个变量:体积(亦或者是重量)v和价值w
初始化好像不是必须的,如果出bug自己又搞不懂是哪里再加上吧
[NOIP2005]采药 登录—专业IT笔试面试备考平台_牛客网
#include <iostream>
#include <vector>
using namespace std;
int dp[1000];
int p[101];
int t[101];
int main() {int v,n;cin>>v>>n;for(int i=0;i<101;i++){p[i]=0;t[i]=0;}for(int i=0;i<100;i++){dp[i]=0;}for(int i=0;i<n;i++){cin>>t[i]>>p[i];}for(int i=0;i<n;i++){for(int j=v;j>=t[i];j--){ //注意是大于等于,有等于!这里错过好几次dp[j]=max(dp[j],dp[j-t[i]]+p[i]);}}cout<<dp[v];
}
P1507 NASA的食物计划NASA的食物计划 - 洛谷
来个二维数组版的例子。
#include <iostream>
#include <vector>
using namespace std;
int dp[500][500];
int h1[401];
int t1[401];
int k1[501];
int main() {int h,t,n;cin>>h>>t>>n;//初始化 for(int i=0;i<400;i++){h1[i]=0;t1[i]=0;}for(int i=0;i<500;i++){k1[i]=0;}for(int i=0;i<n;i++){cin>>h1[i]>>t1[i]>>k1[i];}for(int i=0;i<n;i++){for(int j=h;j>=h1[i];j--){for(int k=t;k>=t1[i] ;k--){dp[j][k]=max(dp[j][k],dp[j-h1[i]][k-t1[i]]+k1[i]);}}}cout<<dp[h][t];
}二、 完全背包
一般输入两个变量:体积(亦或者是重量)v和价值w
完全背包的意思就是每个物品可以取无限次,0-1背包是每个物品只能取走一次。
完全背包例题:3. 完全背包问题 - AcWing题库
#include <iostream>
#include <vector>
#include<bits/stdc++.h>
using namespace std;
int dp[1001];
int v1[1001];
int w[1001];
int main() {int n,v;cin>>n>>v;for(int i=0;i<n;i++){cin>>v1[i]>>w[i];}for(int i=0;i<n;i++){for(int j=v1[i];j<=v;j++){ //差别在这里dp[j]=max(dp[j],dp[j-v1[i]]+w[i]);}}cout<<dp[v];
}注意:可以看出,0-1背包和完全背包的问题的解决方案差别不大,主要就是在for(int j=v……部分的差别。
三、多重背包问题
一般输入两个变量:体积(亦或者是重量)v、价值w和数量s
背包问题中最难的了,结合了0-1背包和多重背包的特点,简单来说就是某个物品可以取s次,有了次数限制。
常规思路就是拆分成份,重新构成0-1背包问题。
例题4. 多重背包问题 I - AcWing题库
#include <iostream>
#include <vector>
#include<bits/stdc++.h>
using namespace std;
int dp[1001];
int v1[1001];
int w[1001];
int s[1001];
int main() {int n,v;cin>>n>>v;for(int i=0;i<n;i++){cin>>v1[i]>>w[i]>>s[i];}for(int i=0;i<n;i++){while(s[i]!=0){ //监控数量for(int j=v;j>=v1[i];j--){ //0-1背包处理dp[j]=max(dp[j],dp[j-v1[i]]+w[i]);}s[i]--;}}cout<<dp[v];
}可以看到,for(int j=v……这部分的处理和0-1背包的处理逻辑一样。就是在外面增加一个while监控数量的变化即可。整体还是在for(int i=0;i<n;i++){框架下。
上述的微小改进只适用于处理小范围数据集,数据集一大(一两千)就会超时,此时就需要改进算法了,参考下题:
数据量大的情况:5. 多重背包问题 II - AcWing题库
二进制优化是基于这样的事实:
任意正整数可以表示为2的幂之和。
利用这一点,我们可以将每种物品的数量拆分成几个二进制的组件,从而将多重背包问题转换为0-1背包问题的多个实例。
二进制拆分挺麻烦的……要加里面,我写了一版有的用例没有过,还需要再背2024年5月6日
#include <bits/stdc++.h>
using namespace std;
int dp[2102];
int v1[2101];
int w[2101];
int s[2001];int main() {int n,v;cin>>n>>v;for(int i=0;i<n;i++){cin>>v1[i]>>w[i]>>s[i];}for(int i=0;i<n;i++){if(s[i]*v1[i]>=v){ //份数乘以重量 大于 容量,采取完全背包。 for(int j=v1[i];j<=v;j++){dp[j]=max(dp[j],dp[j-v1[i]]+w[i]);}}else{// 二进制拆分,处理多重背包问题for(int k=1;s[i]>0;k=k*2){if(k>s[i]){// 当拆分块大于剩余数量时,调整k为剩余数量k=s[i];}int totalv=k*v1[i];int totalw=k*w[i];for(int j=v;j>=totalv;j--){//0-1背包处理 dp[j]=max(dp[j],dp[j-totalv]+totalw);}s[i]=s[i]-k;}}}cout<<dp[v];return 0;
}四、分组背包问题
分组背包问题:9. 分组背包问题 - AcWing题库
就是分组,每个组只能取一个背包。(这个模板没背过,下次记得背,2024年5月6日)
#include <bits/stdc++.h>
using namespace std;
int dp[102];
int v1[101];
int w[101];int main() {int n,v,z;cin>>n>>v;for(int i=0;i<n;i++){cin>>z;for(int j=0;j<z;j++){ cin>>v1[j]>>w[j];}for(int k=v;k>=0;k--){for(int j=0;j<z;j++){if(k>=v1[j]){dp[k]=max(dp[k],dp[k-v1[j]]+w[j]); }}}}cout<<dp[v];return 0;
}
相关文章:
)
【中等】保研/考研408机试-动态规划1(01背包、完全背包、多重背包)
背包问题基本上都是模板题,重点:弄熟多重背包模板 dp[j]max(dp[j-v[i]]w[i],dp[j]) //核心思路代码(一维数组版) dp[i][j]max(dp[i-1][j], dp[i-1][j-v[i]]w[i])//二维数字版 一、 0-1背包 一般输入两个变量:体积&…...

[DEMO]给两个字符串取交集的词语
要求:2个英文字符串中,取相同的大于等于4个字母的词组 比如: 字符串1:" xingMeiLingabcdef WorldHello", 字符串2:"mnjqlup WorldLingLing xingMeiLingHello" 获取交接: [xingMeiLing…...

leetcode53-Maximum Subarray
题目 给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。 子数组 是数组中的一个连续部分。 示例 1: 输入:nums [-2,1,-3,4,-1,2,1,-5,4] 输出…...

Python 基于 OpenCV 视觉图像处理实战 之 OpenCV 简单人脸检测/识别实战案例 之七 简单进行人脸检测并添加面具特效实现
Python 基于 OpenCV 视觉图像处理实战 之 OpenCV 简单人脸检测/识别实战案例 之七 简单进行人脸检测并添加面具特效实现 目录...
【go项目01_学习记录06】
学习记录 1 使用中间件1.1 测试一下1.2 push代码 2 URI 中的斜杆2.1 StrictSlash2.2 兼容 POST 请求 1 使用中间件 代码中存在重复率很高的代码 w.Header().Set("Content-Type", "text/html; charsetutf-8")统一对响应做处理的,我们可以使用中…...
Vue中Element的下载
打开vscode让项目在终端中打开 输入npm install element-ui2.15.3 然后进行下载 在node_modules中出现element-ui表示下载完成 然后在输入Vue.use(ElementUI); import Vue from vue import App from ./App.vue import router from ./router import ElementUI from element-ui…...

机器人项目相关
机器人项目相关 1. Nvidia 1.1 Jetson 1.1.1 初步安装Riva教程 llamaspeakJetson AGX Orin踩坑记录(1)安装Riva 参考知乎链接:https://zhuanlan.zhihu.com/p/670007305 1.1.2 NVIDIA Jetson AI Lab 借助 NVIDIA Jetson™ 将生成式 AI…...

Mac升级go版本某种错误情况处理
当看到 "go1.21 is keg-only, which means it was not symlinked into /opt/homebrew" 这样的信息时,意味着Homebrew没有自动为你创建指向新版本Go的符号链接(symlink),因为这是一个旧版本Go的替代版本。 Homebrew中的…...
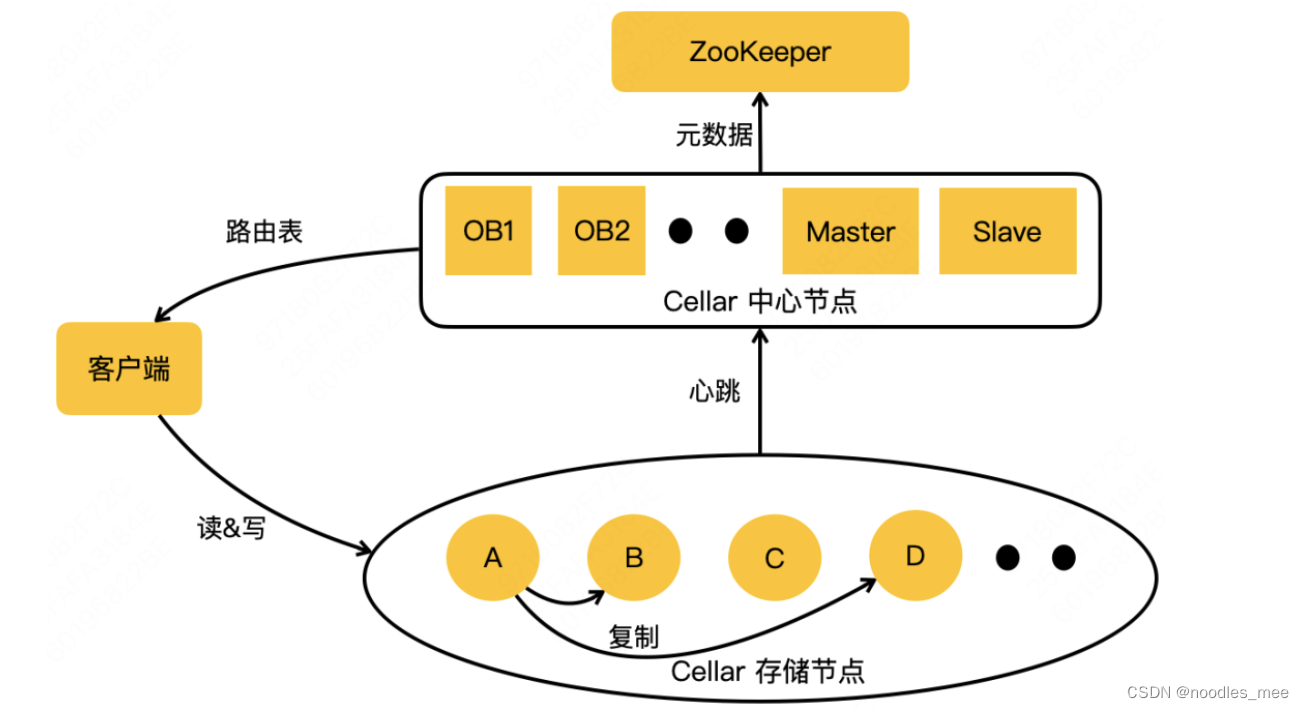
美团KV存储squirrel和Celler学习
文章目录 美团在KV存储squirrel优化和改进在水平方向1、对Gossip协议进行优化 在垂直扩展方面1、forkless RDB数据复制优化2、使用多线程,充分利用机器的多核能力 在高可用方面 美团持久化kv存储celler优化和改进水平扩展优化1、使用bulkload进行数据导入2、线程模型…...
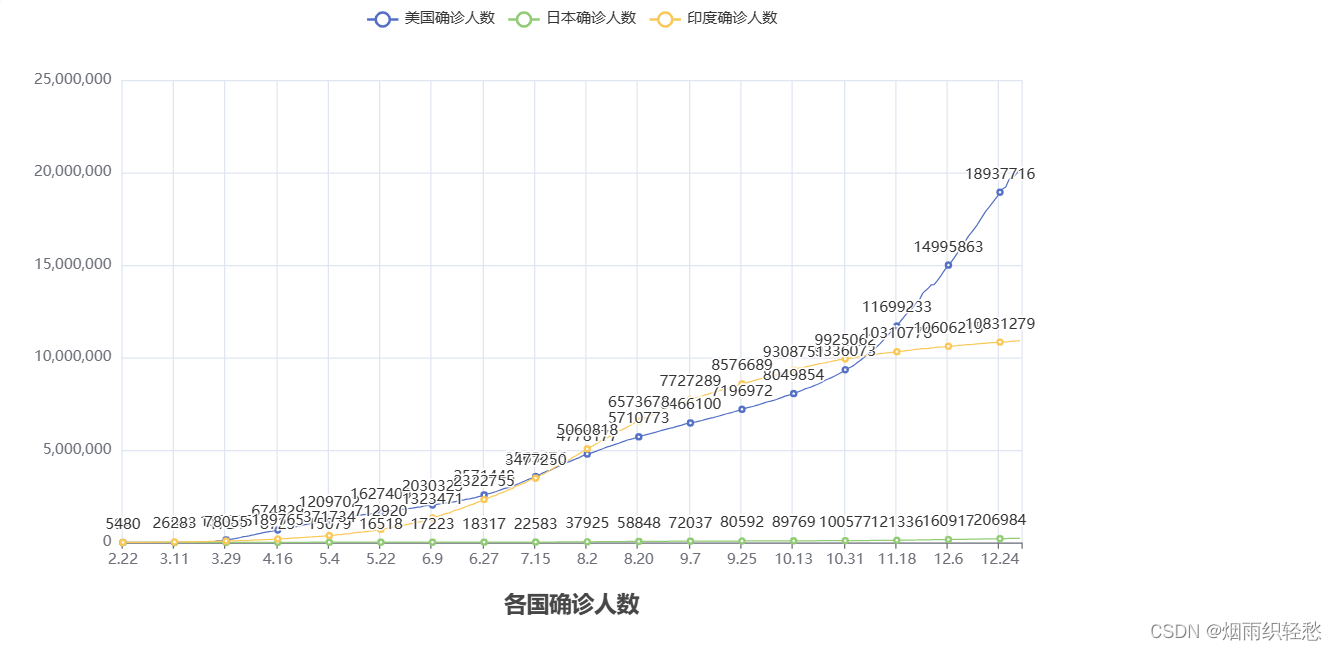
Python学习笔记------处理数据和生成折线图
给定数据: jsonp_1629344292311_69436({"status":0,"msg":"success","data":[{"name":"美国","trend":{"updateDate":["2.22","2.23","2.24",&qu…...
——MindMap)
知识图谱与大语言模型的协同(RAG)——MindMap
MindMap : Knowledge Graph Prompting Sparks Graph of Thoughts in Large Language Models 论文地址: https://arxiv.org/abs/2308.09729 代码:https://github.com/wylwilling/MindMap 1.概述 大型语言模型(LLMs)在处理新信息、防止生成幻觉内容、以及增强决策过程透明度…...

奶爸预备 |《P.E.T.父母效能训练:让亲子沟通如此高效而简单:21世纪版》 / 托马斯·戈登——读书笔记
目录 引出致中国读者译序前言第1章 父母总是被指责,而非受训练第2章 父母是人,不是神第3章 如何听,孩子才会说:接纳性语言第4章 让积极倾听发挥作用第5章 如何倾听不会说话的婴幼儿第6章 如何听,孩子才肯听第8章 通过改…...
【WebGIS实例】(13)MapboxGL 加载地形高程数据
前言 官网示例:Add 3D terrain to a map | Mapbox GL JS | Mapbox 大佬博客:Mapbox GL基础(七):地形数据的处理与加载 (jl1mall.com) 加载Mapbox地形数据 map.once(style.load, () > {map.addSource(mapbox-dem,…...

Node.js -- MongoDB
文章目录 1. 相关介绍2. 核心概念3. 命令行交互3.1数据库命令3.2 集合命令3.3 文档命令 4. 数据库应用场景4.1 新增4.2 删除4.3 更新4.4 查询 5. 图形化工具Robo 3T 1. 相关介绍 一、简介 Mongodb是什么 MongoDB是一个基于分布式文件存储的数据库,官方地址https://…...

语音识别--单声道转换与降采样
⚠申明: 未经许可,禁止以任何形式转载,若要引用,请标注链接地址。 全文共计3077字,阅读大概需要3分钟 🌈更多学习内容, 欢迎👏关注👀【文末】我的个人微信公众号…...
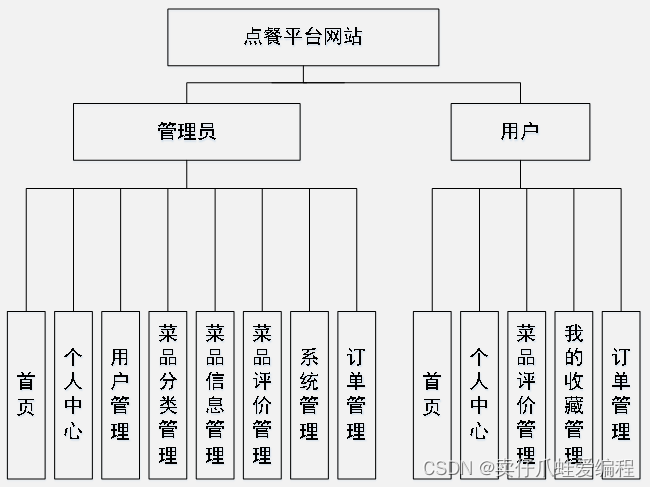
基于springboot+vue+Mysql的点餐平台网站
开发语言:Java框架:springbootJDK版本:JDK1.8服务器:tomcat7数据库:mysql 5.7(一定要5.7版本)数据库工具:Navicat11开发软件:eclipse/myeclipse/ideaMaven包:…...

数据库优化
一、主从读写分离 主库:主要负责数据的写入。 从库:主要负责数据的查询。 引出问题: 可能会存在主从延迟,导致主从一致性问题。查询主库的量级需要控制。数据量庞大,索引也占据存储空间,磁盘空间不足,当主库宕机后会影响所有模块的写入,需要进行数据分片,因此引出分库…...
专业渗透测试 Phpsploit-Framework(PSF)框架软件小白入门教程(一)
本系列课程,将重点讲解Phpsploit-Framework框架软件的基础使用! 本文章仅提供学习,切勿将其用于不法手段! Phpsploit-Framework(简称 PSF)框架软件,是一款什么样的软件呢? Phpspl…...
Web安全研究(七)
NDSS 2023 开源地址:https://github.com/bfpmeasurementgithub/browser-fingeprint-measurement 霍普金斯大学 文章结构 introbackground threat model measurement methodology step1: traffic analysisstep2: fingerprint analysis dataset attack statisticsbro…...

矩池云jupyter运行opengait代码 未完成版
文章目录 前言——矩池云的使用技巧1.切换源 一、下载数据集二、下载模型三、环境配置1.查看python、torch、torchvision版本2.查看一些包版本是否过高3.下载包 四、开始训练1.设置环境变量2.遇到的问题(1)torch.cuda.is_available()返回false࿰…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...
