python之 函数相关知识解析
01 函数的注释与嵌套
1.函数的注释
函数的注释与普通注释的区别:用来说明当前函数的参数含义
param 参数名: 参数的注释信息
return: 函数的返回值
例如:
def fun1(name):""":param name: 参数的注释信息:return: 函数的返回值"""print("fun1函数") # 查看源码的快捷键:Ctrl + 左键 点击要查看的函数def fun2(name, age, addr, sal):""":param name: 请输入姓名:param age: 请输入年龄:param addr: 请输入地址:param sal: 请输入薪资:return: 函数执行后的返回信息"""print("fun2函数")# fun1()
# fun2()# lst1 = [1, 2]
# lst1.append()# 打印函数的注释
print(fun1.__doc__)
print(print.__doc__)2.函数的嵌套:
一个函数的内部调用另一个函数
# def fun1():
# print("欢迎来到七夜老师的课堂!")
# fun2() # 陷入死循环的情况
#
#
# def fun2():
# print("VIP 234 班级的直播课!")
# fun1() # 调用fun1函数
#
#
# # 问题:想在调用fun2函数的同时,去调用fun1函数?
# fun2() # 调用fun2函数一个函数的内部嵌套另一个函数
def fun3():print("qsdd!")def fun4():print("秋殇大大")fun4()# 问题1:运行fun3函数,会打印几句话?
# fun3()
# 如果不调用函数,是不会去运行函数的内部代码的!!!# 问题2:能不能在最外层,调用fun4函数?
# fun4() # name 'fun4' is not defined
# 在函数的内部定义的函数,不能直接在最外层调用 -- 函数的作用域# 问题3:那么怎么去调用fun4函数呢?
# 应该在fun4函数定义的同级
fun3()2 python中的内置函数
1.作用域函数(重点)
作用域:定义的变量和函数在哪个范围内可用
文件和文件之间定义的东西,一般不能直接用
函数内定义的东西,不能在文件中直接使用,哪怕同一个文件也不行
类中定义的东西,只在类的内部生效,不能在文件中直接使用
变量:
全局变量 -- 在当前文件内定义的变量,可以在文件任何地方使用
局部变量 -- 在有效范围内可以调用,出了范围就不能用了
类声明的变量也是一样
局部变量在定义的时候可以直接声明为全局变量
局部变量,定义成全局变量
通过global关键字,先声明变量,然后再去赋值
# def fun6():
# b = 5 # 未声明
# global c # 已声明
# c = 6
#
#
# fun6()
# # 哪怕是通过global关键字,转化成全局变量,也不可以直接使用,必须使声明的代码被执行 (注意)
# print(c)数学函数
abs() 绝对值
print(abs(-1)) # 1
divmod() 返回商和余数
x = int(input("请输入一个整型:"))a, b = divmod(x, 2)print(f"商:{a}")
print(f"余:{b}")round() 四舍五入(银行家算法)
# print(round(1.5)) # 2
# print(round(3.5)) # 4
# print(round(5.5)) # 6
#
# print(round(2.5)) # 2
# print(round(4.5)) # 4
# print(round(6.5)) # 6# print(round(4.9))
# print(round(4.6))
# print(round(4.51))看是奇数还是偶数,奇数:四舍五入 偶数:直接舍弃,只在0.5奏效
pow() 次方
print(pow(10, 2))
sum() 求和
min() 最小值
max() 最大值
3 匿名函数
1.匿名函数的定义:
匿名函数:就是没有名字的函数
python lambda表达式实现匿名函数
语法规则:
lambda 参数: 逻辑
匿名函数里面的参数名称,是自定义
结果就是返回表达式的结果
示例:
import math # 导入# pai = math.pi
# print(f"圆周率π: {pai}")
#
# # 圆的面积计算公式: s = π * r²
# r = 5 # 圆的半径
# s = math.pi * pow(r, 2)
# print(f"圆的面积: {s}")# 方式一:普通的函数定义
def s_area(r):""":param r: 圆的半径:return: 返回圆的面积"""s = math.pi * pow(r, 2)return sprint(f"当r的值为5的时候,圆的面积: {s_area(r=5)}")# 方式二:匿名函数的定义
res = lambda r: math.pi * pow(r, 2)
print(f"当r的值为5的时候,圆的面积: {res(r=5)}")04 装饰器之函数传递
1.函数的传递
python中可以把函数当变量传递
所以这种情况下,可以直接执行被传入的函数\
# def fun1(): # print("ddddd ")
# 函数的调用 -- 函数的名称(),就会执行函数的内部代码 # fun1()
# print(fun1) # <function fun1 at 0x7fbb180c8160>, function代表是一个函数、fun1表示函数的名称、at 0x7fbb180c8160表示函数所在的内存地址
示例如下
def fun1():print("qsdd!")def fun2(fun_name): # 参数的名称可以自定义""":param fun_name: 传入函数的引用/本体:return: 调用传入的这个函数"""print("秋殇大大!")print(f"此时fun_name获取的值:{fun_name}") # fun1函数的引用 -- 引用与调用之间的区别:有没有小括号fun_name() # 请问:这是在调用哪个函数? -- 调用fun1函数# 通过函数的引用,来完成,调用fun2函数的时候,去调用fun1函数
fun2(fun_name=fun1) # 把fun1函数,当做变量进行传值函数加小括号,表示调用,没有小括号,表示引用
相关文章:

python之 函数相关知识解析
01 函数的注释与嵌套 1.函数的注释 函数的注释与普通注释的区别:用来说明当前函数的参数含义 param 参数名: 参数的注释信息 return: 函数的返回值 例如: def fun1(name):""":param name: 参数的注释信息:return: 函数的返回值"…...
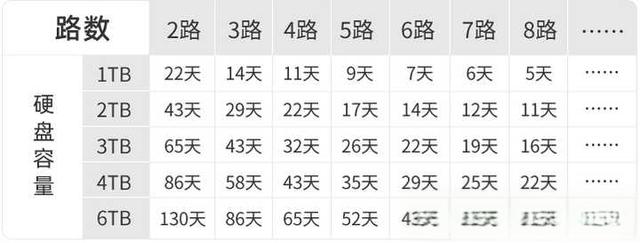
监视器和显示器的区别,普通硬盘和监控硬盘的区别
监视器与显示器的区别,你真的知道吗? 中小型视频监控系统中,显示系统是最能展现效果的一个重要环节,显示系统的优劣将直接影响视频监控系统的用户体验满意度。 中小型视频监控系统中,显示系统是最能展现效果的一个重要…...

Linux:升级OpenSSL和OpenSSH
原因是现有版本存在安全漏洞,需要升级到新版本 原有版本和升级后的版本 OpenSSL 1.0.2k-fips 26 Jan 2017 -> OpenSSL 1.1.1w 11 Sep 2023OpenSSH_7.4p1, OpenSSL 1.0.2k-fips 26 Jan 2017 -> OpenSSH_9.5p1, OpenSSL 1.1.1w 11 Sep 2023目录 查看现有版…...
方法的入栈和出栈
一.作用域问题 1.全局作用域 在全局都能进行访问的变量 var a 10;function fn() {var b 20;return a b;}console.log(fn()); 2.局部的作用域 只能在限定的范围内进行访问 function fn() {var b 20;}console.log(b); b is not defined 打印的结果是b这个变量没用定义 3…...

PHP介绍
🐌博主主页:🐌倔强的大蜗牛🐌 📚专栏分类:PHP❤️感谢大家点赞👍收藏⭐评论✍️ 目录 一、PHP是什么? 二、 PHP 文件是什么? 三、PHP能做什么? 四、P…...

接口自动化测试之-requests模块详解
一、requests背景 Requests 继承了urllib2的所有特性。Requests支持HTTP连接保持和连接池,支持使用cookie保持会话,支持文件上传,支持自动确定响应内容的编码,支持国际化的 URL 和 POST 数据自动编码。 二、requests安装 利用p…...
低代码+定制物资管理:创新解决方案探析
引言 在当今快速变化的商业环境中,企业面临着不断增长的挑战,如提高效率、降低成本、满足客户需求等。为了应对这些挑战,企业需要不断创新并采用先进的技术解决方案。在这样的背景下,低代码开发和定制化物资管理成为了引领企业变…...

13 【PS作图】人物绘画理论-脸型
三庭五眼 三庭:脸的长度比例 (1)发际线到眉毛 (2)眉毛到鼻底 (3)鼻底到下巴 三个部分大致为三等分 五眼:脸的宽度比例 以眼睛长度为单位,把脸的宽度分成五等分&#x…...
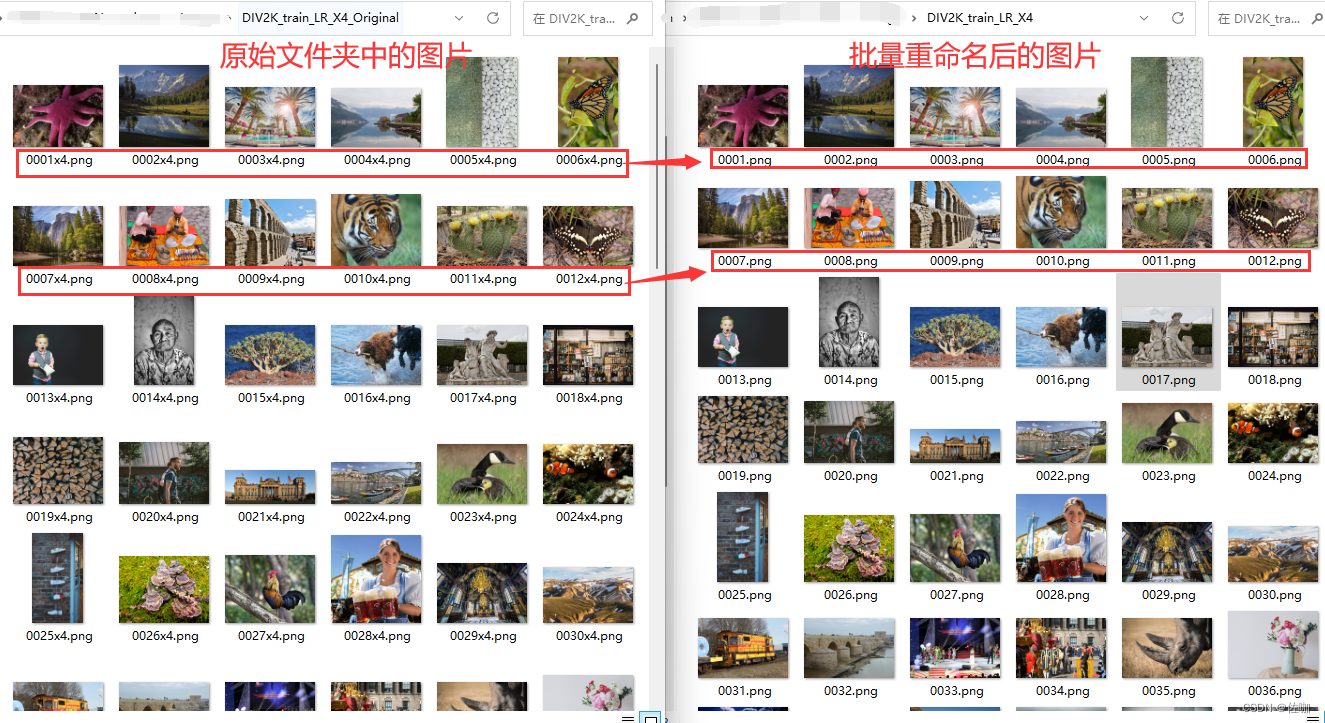
Python批量修改图片文件名中的指定名称
批量处理图像时,图片名有时需要统一,本教程仅针对图片中名如:0001x4.png,批量将图片名中的x4去除,只留下0001.png的情况。 如果想要按照原图片顺序批量修改图片名,参考其它博文:按照原顺序批量…...
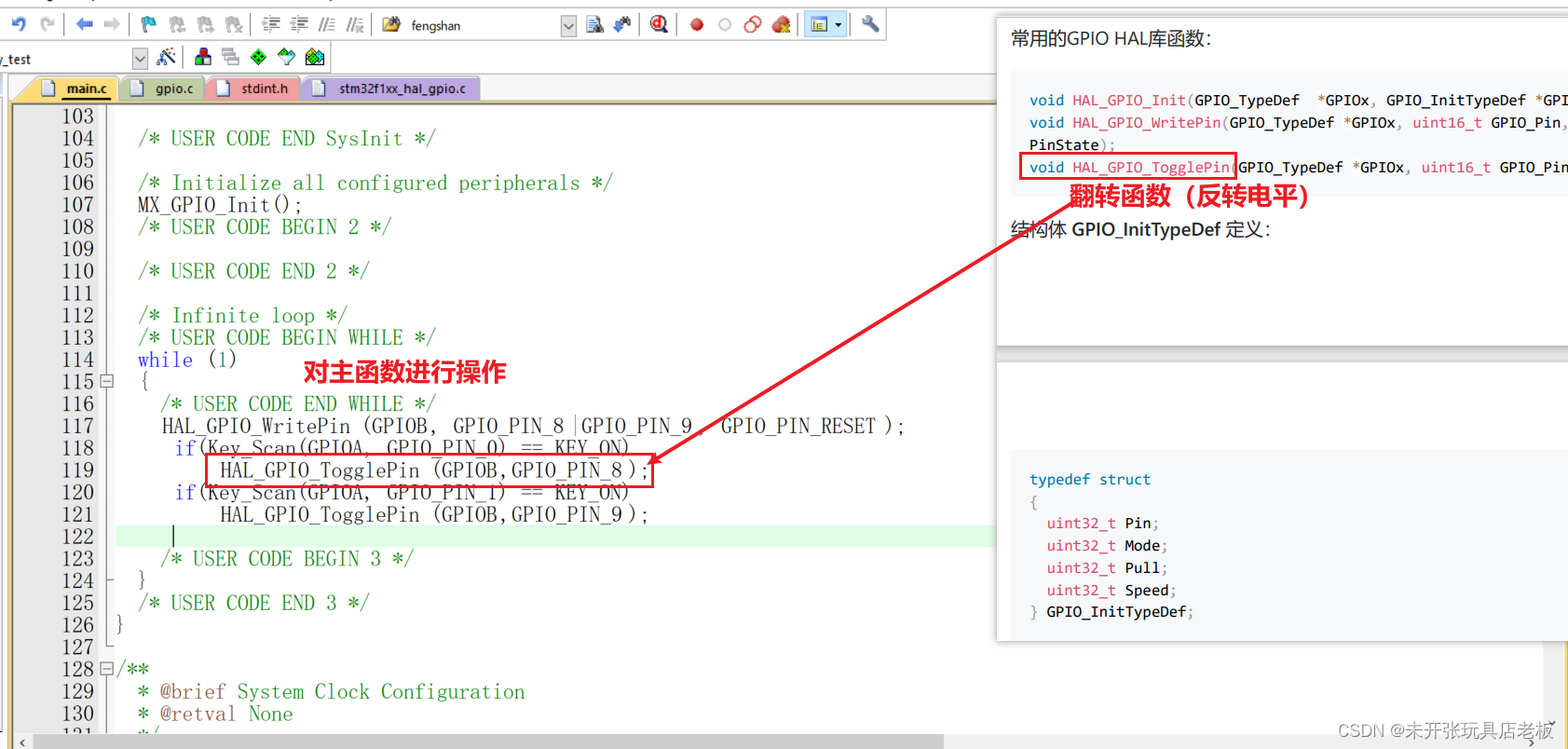
STM32点灯大师(点了一颗LED灯,轮询法)
配置操作: 一、使用CubeMX配置到大致的操作 1.1 选择芯片 1.2 选择引脚(根据电路图) 1.3 配置gpio口 1.4 配置系统 1.5文件项目操作 最后就是点击 二、点击CubeMX生成的代码,并且修改代码 2.1 看看效果 2.2 写代码...

动态规划算法:路径问题
例题一 解法(动态规划): 算法思路: 1. 状态表⽰: 对于这种「路径类」的问题,我们的状态表⽰⼀般有两种形式: i. 从 [i, j] 位置出发,巴拉巴拉; ii. 从起始位置出…...

盘一盘接口测试的那些痛点,你现在会解决了吗
前言 说到接口测试,想必大家一定不会陌生。接口测试就是测试系统组件间,接口对接是否顺畅的一种测试。包括测试数据能否交换、能否传递、能否正常控制管理过程,以及系统间的相互逻辑依赖关系,等等。 由于接口测试主要是检测系统…...

基于alpha shapes的边缘点提取(matlab)
1、原理介绍 由Edelsbrunner H提出的alpha shapes算法是一种简单、有效的快速提取边界点算法。其克服了点云边界点形状影响的缺点,可快速准确提取边界点。如下图所示,对于任意形状的平面点云,若一个半径为a的圆,绕其进行滚动&…...

C#三人飞行棋
C#三人飞行棋 #region 1控制台设置int w 50, h 30; ConsoleInit(w, h); #endregion#region 2 场景选择实例//声明一个表示场景标识的变量 E_SceneType nowSceneType new E_SceneType(); while (true) {switch (nowSceneType){case E_SceneType.Begion://开始场景逻辑Consol…...
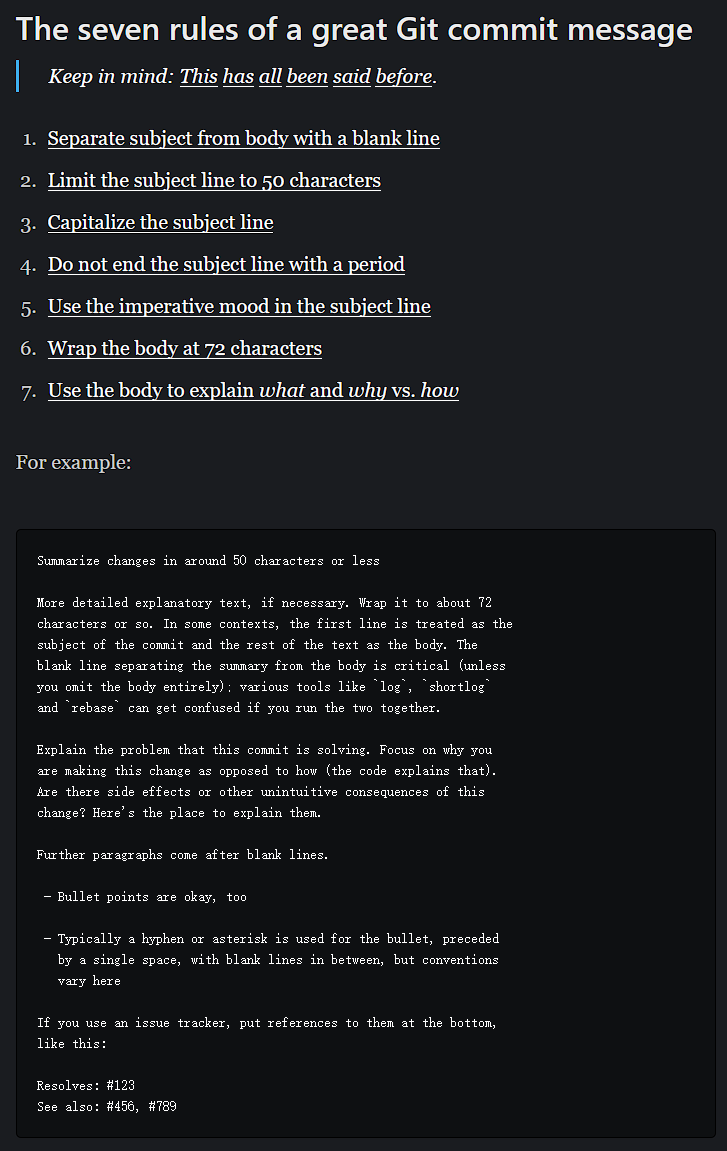
Notes for the missing semester. Useful and basic knowledge about Linux.
The Shell Contents The first course is to introduce some simple commands. I’ll list some commands that I’m not familiar with: # --silent means dont give log info, # --head means we only want the http head. curl --head --silent bing.com.cn# cut --deli…...

【信息系统项目管理师知识点速记】资源管理基础
项目团队 执行项目工作,实现项目目标的一组人员。成员具备不同技能,可全职或兼职,随项目进展而变化。参与项目规划和决策,贡献专业技能,增强对项目的责任感。项目管理团队 直接参与项目管理活动的成员,负责项目管理和领导。负责项目各阶段的启动、规划、执行、监督、控制…...

Android性能优化面试题汇总
Android的性能优化涉及多个方面,如启动优化、稳定性优化、内存优化、网络优化、电量优化、安全优化等方面。 一、稳定性优化 1.1 你们做了哪些稳定性方面的优化 随着项目的逐渐成熟,用户基数逐渐增多,DAU持续升高,我们遇到了很多稳定性方面的问题,对于我们技术同学遇到…...
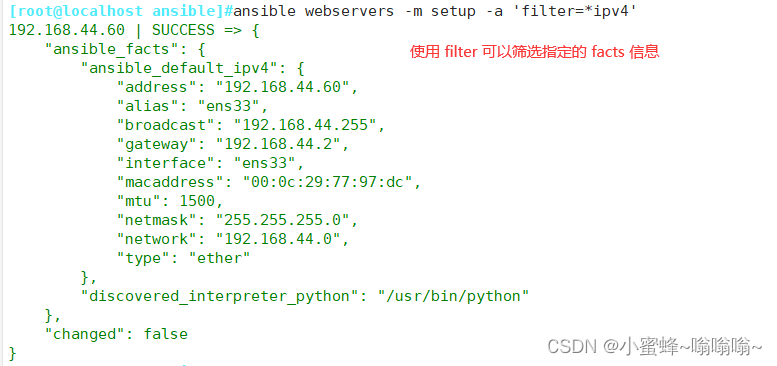
Ansible 自动化运维工具 - 了解和模块应用
目录 一. Ansible 的相关知识 1.1 Ansible 工具的简介 1.2 Ansible的四大组件 1.3 运维自动化工具 1.4 Ansible 和其它自动化运维工具对比 1.5 Ansible 的优缺点 二. Ansible 环境安装部署 2.1 管理端安装 ansible 2.2 配置主机清单 三. ansible 命令行模块 3.1 comm…...
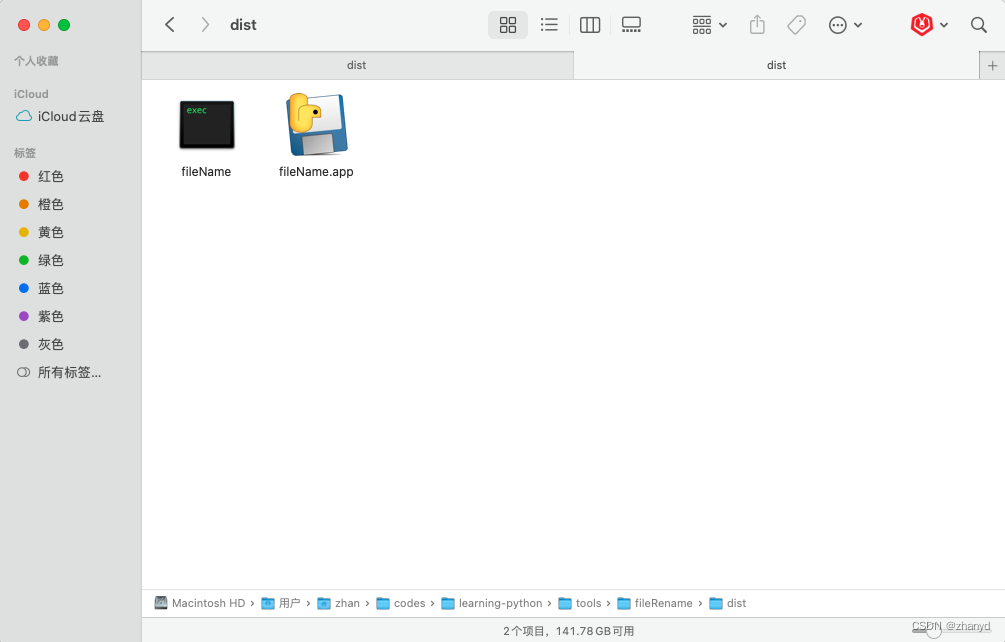
AI神助攻!小白也能制作自动重命名工具~
我们平时从网上下载一些文件,文件名很多都是一大串字母和数字,不打开看看,根本不知道里面是什么内容。 我想能不能做个工具,把我们一个文件夹下面的所有word、excel、ppt、pdf文件重命名为文件内容的第一行。 我们有些朋友可能不会…...
(读书笔记-大模型) LLM Powered Autonomous Agents
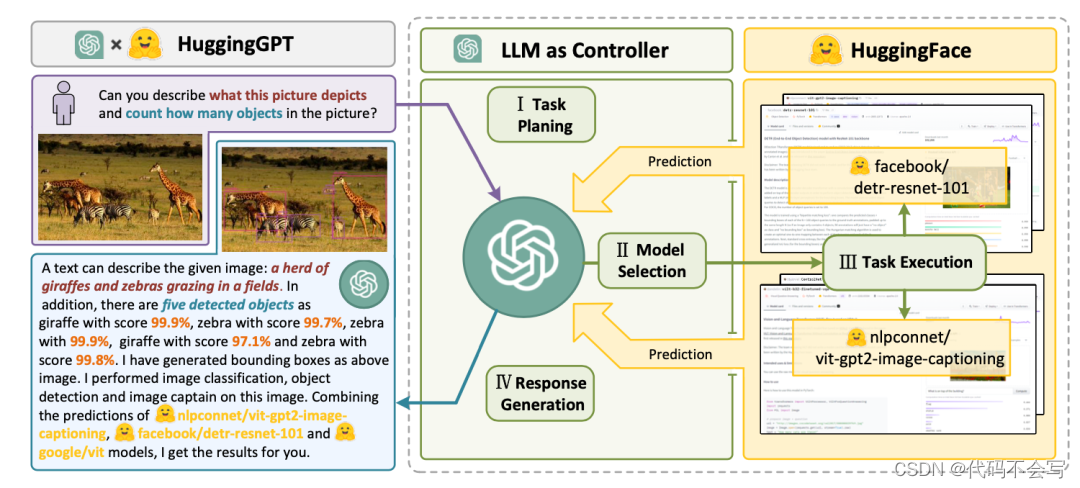
目录 智能体系统的概念 规划组件 记忆组件 工具组件 案例研究 智能体系统的概念 在大语言模型(LLM)赋能的自主智能体系统中,LLM 充当了智能体的大脑,其三个关键组件分别如下: 首先是规划,它又分为以下…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

高效的后台管理系统——可进行二次开发
随着互联网技术的迅猛发展,企业的数字化管理变得愈加重要。后台管理系统作为数据存储与业务管理的核心,成为了现代企业不可或缺的一部分。今天我们要介绍的是一款名为 若依后台管理框架 的系统,它不仅支持跨平台应用,还能提供丰富…...

Vue 实例的数据对象详解
Vue 实例的数据对象详解 在 Vue 中,数据对象是响应式系统的核心,也是组件状态的载体。理解数据对象的原理和使用方式是成为 Vue 专家的关键一步。我将从多个维度深入剖析 Vue 实例的数据对象。 一、数据对象的定义方式 1. Options API 中的定义 在 Options API 中,使用 …...
