【卷积神经网络】激活函数 | Tanh / Sigmoid / ReLU / Leaky ReLU / ELU / SiLU / GeLU
文章目录
- 一、Tanh
- 二、Sigmoid
- 三、ReLU
- 四、Leaky ReLU
- 五、ELU
- 六、SiLU
- 七、Mish
本文主要介绍卷积神经网络中常用的激活函数及其各自的优缺点
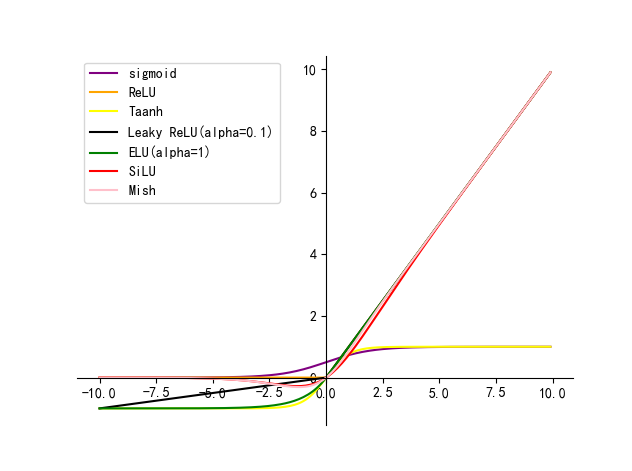
最简单的激活函数被称为线性激活,其中没有应用任何转换。 一个仅由线性激活函数组成的网络很容易训练,但不能学习复杂的映射函数。线性激活函数仍然用于预测一个数量的网络的输出层(例如回归问题)。
非线性激活函数是更好的,因为它们允许节点在数据中学习更复杂的结构 。两个广泛使用的非线性激活函数是 sigmoid 函数和 双曲正切 激活函数。
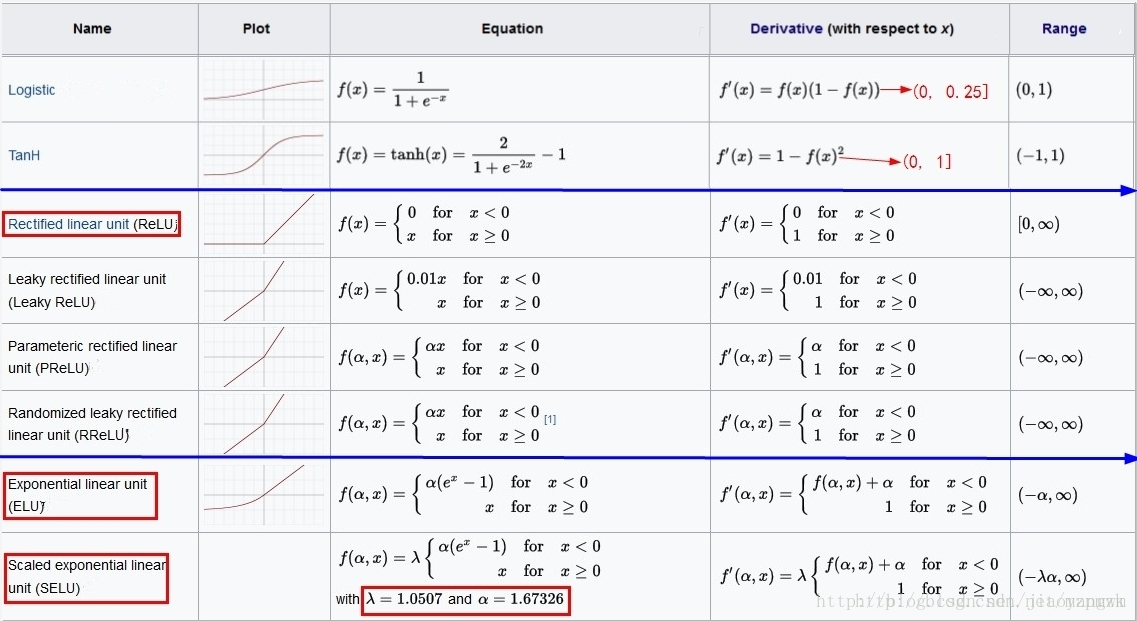
一、Tanh
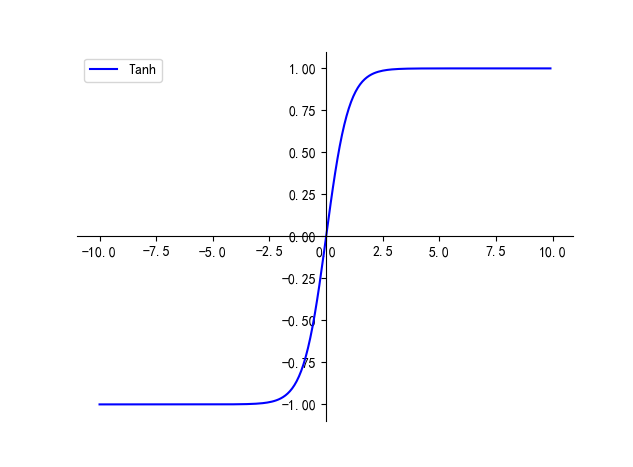
Tanh 函数公式如下,数值范围在 (-1, 1),导数范围为 (0, 1]
Tanh 函数的优点:
- 以 0 为中心,能够达到正负平衡,避免出现梯度的不稳定性
Tanh 函数的缺点:
- 会导致梯度消失问题!
二、Sigmoid

Sigmoid 函数公式如下,数值范围为 (0, 1),导数范围为 (0, 0.25]:
- f(x)=11+e−zf(x) = \frac{1}{1+e^{-z}}f(x)=1+e−z1
sigmoid 函数优点:
- 可以把输入映射到 (0, 1)区间,可以用来表示概率,在物理意义上最为接近生物神经元
sigmoid 函数缺点:
- 梯度消失问题 :由于 sigmoid 的导数 f′(zl) 区间为 (0, 0.25],所以其极易落入饱和区,导致梯度非常小,权重接近不变,无法正常更新
- sigmoid 的输出并不是均值为 0 的,所有输出数据的大于0,会增加梯度的不稳定性
- 当输出接近饱和或剧烈变化时,对输出范围的这种缩减往往会带来一些不利影响
三、ReLU
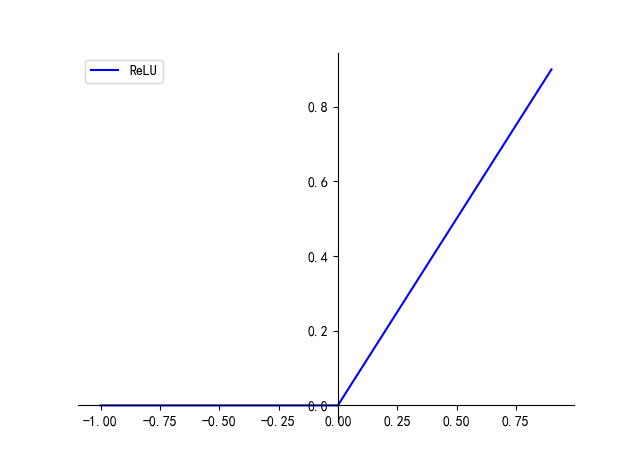
f(x)=max(0,x)f(x) = \text{max}(0, x)f(x)=max(0,x)
ReLU 函数的优点:
- 摒弃了复杂的计算, 比 sigmoid/tanh 收敛的更快 (大概快 6x)
- 其导数在其权重和(z) 大于 0 的时候为 1,不存在梯度消失现象权重可以正常更新,但也要防止 ReLU 的梯度爆炸
ReLU 函数的缺点:
- 小于 0 的输出经过 ReLU 之后会全都变成 0,梯度值为0,从而权重无法正常更新
- 输出具有偏移现象,即输出均值恒大于零
- 当使用了较大的学习速率时,易受到饱和的神经元的影响。
四、Leaky ReLU
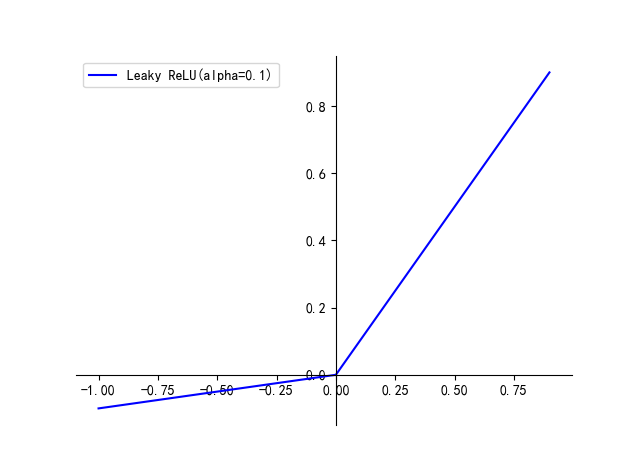
公式如下:
- f(x)=αx,x<0f(x) = \alpha x, \ x<0f(x)=αx, x<0
- f(x)=x,x>=0f(x) = x, \ x>=0f(x)=x, x>=0
为了防止模型 dead 的情况,出现了很多 ReLU 的改进版本,如 Leaky ReLU,在 0 右侧和 ReLU 一样,左侧从全零变成了一个斜率很小的直线
优点:
- 避免了小于零的特征被处理为 0 导致特征丢失的情况,同时左右两侧梯度都是恒定的,不会出现梯度消失现象
缺点:
- Leaky ReLU中的 α\alphaα 为常数,一般设置 0.01。这个函数通常比 ReLU 激活函数效果要好,但是效果不是很稳定,所以在实际中 Leaky ReLU 使用的并不多。
五、ELU
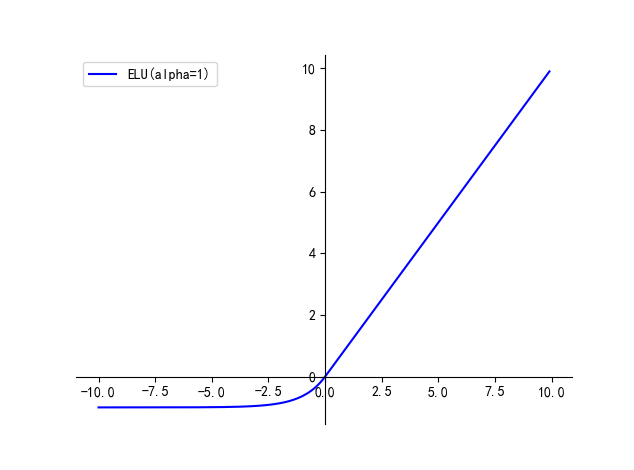
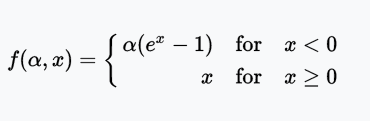
ELU(Exponential Linear Unit,指数线性单元)尝试加快学习速度。基于ELU,有可能得到比ReLU更高的分类精确度。
优点:
- 解决了 ReLU 可能导致的网络 dead 的问题
缺点:
- 计算量较大
六、SiLU
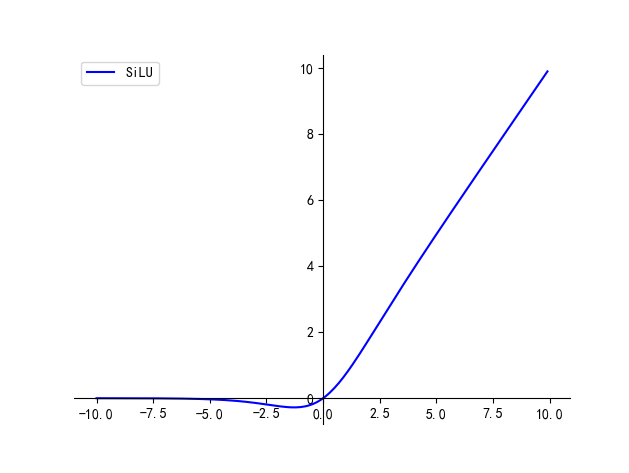
f(x)=x∗sigmoid(βx)f(x) = x *\text{sigmoid}(\beta x)f(x)=x∗sigmoid(βx),β=1\beta=1β=1 时就是 SiLU
优点:
- 相比 ReLU 增加了平滑性的特点
缺点:
- 引入了指数计算,增加了计算量
七、Mish
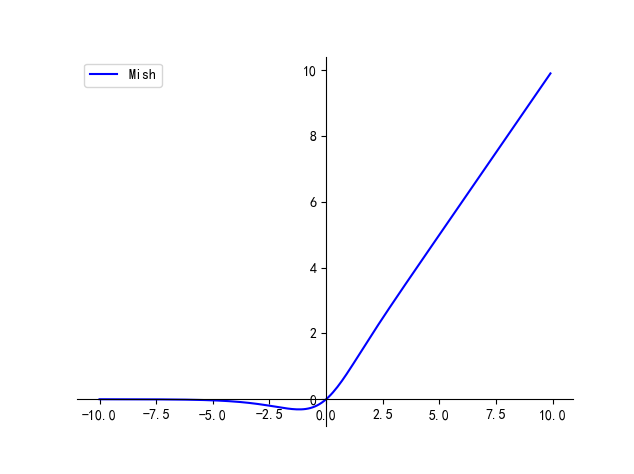
f(x)=x∗tanh(ln(1+ex))f(x) = x * \text{tanh}(\text{ln}(1+e^x))f(x)=x∗tanh(ln(1+ex))
优点:
- 平滑、非单调、无上界、有下界
缺点:
- 引入了指数函数,增加了计算量
相关文章:

【卷积神经网络】激活函数 | Tanh / Sigmoid / ReLU / Leaky ReLU / ELU / SiLU / GeLU
文章目录一、Tanh二、Sigmoid三、ReLU四、Leaky ReLU五、ELU六、SiLU七、Mish本文主要介绍卷积神经网络中常用的激活函数及其各自的优缺点 最简单的激活函数被称为线性激活,其中没有应用任何转换。 一个仅由线性激活函数组成的网络很容易训练,但不能学习…...

刷题记录:牛客NC24048[USACO 2017 Jan P]Promotion Counting 求子树的逆序对个数
传送门:牛客 题目描述 奶牛们又一次试图创建一家创业公司,还是没有从过去的经验中吸取教训–牛是可怕的管理者! 为了方便,把奶牛从 1∼n1\sim n1∼n 编号,把公司组织成一棵树,1 号奶牛作为总裁(这棵树的根…...

MpAndroidChart3最强实践攻略
本篇主要总结下Android非常火爆的一个三方库MpAndroidChart的使用。可能在大多数情况下,我们很少会在Android端去开发图表。但如果说去做一些金融财经类、工厂类、大数据类等的app,那么绝对会用到MpAndroidChart。 一、前言 2018年,那年的我…...
:事务管理ACID)
Spring笔记(9):事务管理ACID
一、事务管理 一个数据库事务是一个被视为单一的工作单元操作序列。 事务管理有四个原则,被成为ACID: Atomicity 原子性—— 事务作为独立单元进行操作,整个序列是一体的,操作全都成功或失败。Consistency 一致性—— 引用完整…...

io流 知识点+代码实例
需求 : 如何实现读写文件内部的内容?流 : 数据以先入先出的方式进行流动相当于管道,作用用来传输数据数据源-->流-->目的地流的分类 :流向分 : 以程序为中心输入流输出流操作单元 :字节流 : 万能流字符流 : 只能操作纯文本文件功能分 :节点流 : 真实实现读写的功能流(包…...
【MySQL】P8 多表查询(2) - 连接查询 联合查询
连接查询以及联合查询多表查询概述连接查询内连接隐式内连接显式内连接外连接左外连接右外连接自连接联合查询多表查询概述 建表语句见上一篇博文:https://blog.csdn.net/weixin_43098506/article/details/129402302 e.g.e.g.e.g. select * from emp, dept where e…...
QML动画(Animator)
在Qt5.2之后,引入Animator动画元素。这种方式可以直接所用于Qt Quick的场景图形系统,这使得基于Animator元素的动画及时在ui界面线程阻塞的情况下仍然能通过图形系统的渲染线程来工作,比传统的基于对象和属性的Animation元素能带来更好的用户…...
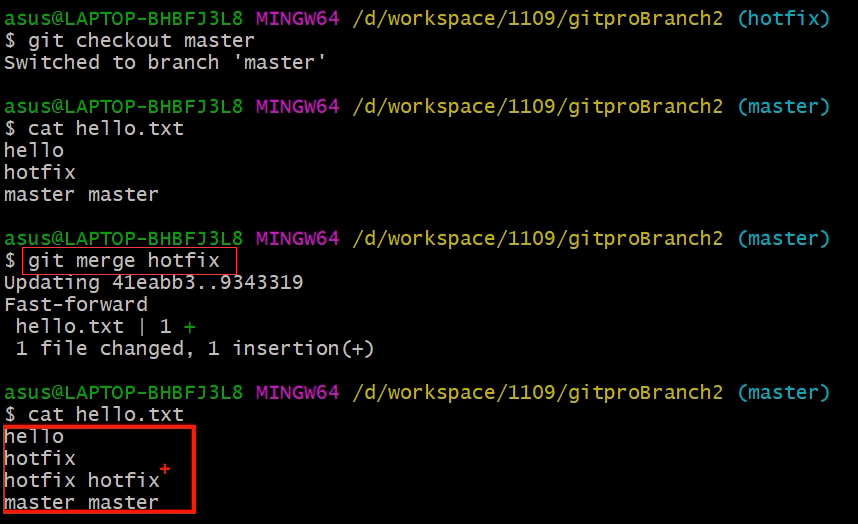
Git 分支操作【解决分支冲突问题】
1. 什么是分支 在版本控制过程中,同时推进多个任务,为每个任务,我们就可以创建每个任务的单独分支。使用分支意味着程序员可以把自己的工作从开发主线上分离开来,开发自己分支的时候,不会影响主线分支的运行。对于初学…...

盘点全球10大女性技术先驱
盘点全球10大女性技术先驱 人们普遍认为技术是男性主导的领域,但事实,技术或编程与性别无关,几乎任何人都可以成为技术大神。已经有很多案例证明女性同样可以在技术领域施展才能。在女神节来临之际,我为大家盘点一下为编程做出卓越…...

C++之dynamic_cast
C之dynamic_cast前言dynamic_castNote:示例:前言 dynamic_cast运算符牵扯到的面向对象的多态性跟程序运行时的状态,所以不能完全的使用传统的转换方式来替代。因此是最常用,最不可缺少的一个运算符,与static_cast一样,dynamic_cas…...

JavaScript 箭头函数、函数参数
箭头函数: 箭头函数是一种更加简洁的函数书写方式箭头函数本身没有作用域(无this)箭头函数的this指向上一层,上下文决定其this基本语法:参数 > 函数体 a. 基本用法 let fn v > v; //等价于 let fn function(…...

JavaScript_Object.keys() Object.values()
目录 一、Object.keys() 二、Object.values() 一、Object.keys() Object.keys( ) 的 用法 : 作用 :遍历对象 { } 返回结果:返回 对象中 每一项 的 key 值 返回值 : 是一个 *** [ 数 组 ] *** 例子 ( 1 ) : <script>// 1. 定义一个对象var obj …...

扬帆优配|高送转+高分红+高增长潜力股揭秘
高送转且高分红的高增加股票,有望跑赢大盘。 此前七连阴的泽宇智能,今日早盘大幅高开。到上午收盘,该股飙涨9.3%,位居涨幅榜前列。音讯面上,3月7日晚间,泽宇智能发表2022年年报,年报显现&#x…...
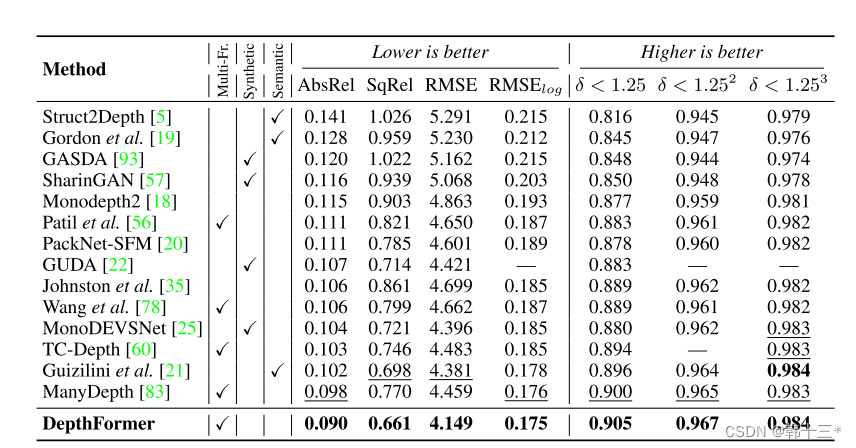
基于transformer的多帧自监督深度估计 Multi-Frame Self-Supervised Depth with Transformers
Multi-Frame Self-Supervised Depth with Transformers基于transformer的多帧自监督深度估计0 Abstract 多帧深度估计除了学习基于外观的特征外,也通过特征匹配利用图像之间的几何关系来改善单帧估计。我们采用深度离散的核极抽样来选择匹配像素,并通过一…...

设计模式: 单例模式
目录单例模式应用场景实现步骤涉及知识点设计与实现单例模式 通过单例模式的方法创建的类在当前进程中只有一个实例; 应用场景 配置管理 日志记录 线程池 连接池 内存池 对象池 消息队列 实现步骤 将类的构造方法定义为私有方法 定义一个私有的静态实例 提供一…...

idea编辑XML文件出现:Tag name expected报错
说明 Tag name expected解释其实就是:需要标记名称,也就是符号不能直接使用的意思 XML (eXtensible Markup Language) 是一种标记语言,用于存储和传输数据。在 XML 中,有些字符被视为特殊字符,这些字符在 XML 中具有…...

第十三届蓝桥杯省赛C++ A组 爬树的甲壳虫(简单概率DP)
题目如下: 思路 or 题解: 概率DP 状态定义: dp[i]dp[i]dp[i] 表示从树根到第 iii 层的期望 状态转移: dp[i](dp[i−1]1)∗11−pdp[i] (dp[i - 1] 1) * \frac{1}{1-p}dp[i](dp[i−1]1)∗1−p1 这个式子的意思是:…...
手动集成Tencent SDK遇到的坑!!!
手动集成的原因 由于腾讯未把Tencent SDK上传到Github中,所以我们不能通过Cocoapods的方式集成,只能通过官方下载其SDK手动集成。 Tencent SDK手动集成步骤 1.访问腾讯开放平台SDK下载界面,找到并下载iOS_SDK_V3.5.1。(目前最新…...
三天吃透mybatis面试八股文
本文已经收录到Github仓库,该仓库包含计算机基础、Java基础、多线程、JVM、数据库、Redis、Spring、Mybatis、SpringMVC、SpringBoot、分布式、微服务、设计模式、架构、校招社招分享等核心知识点,欢迎star~ Github地址:https://github.com/…...
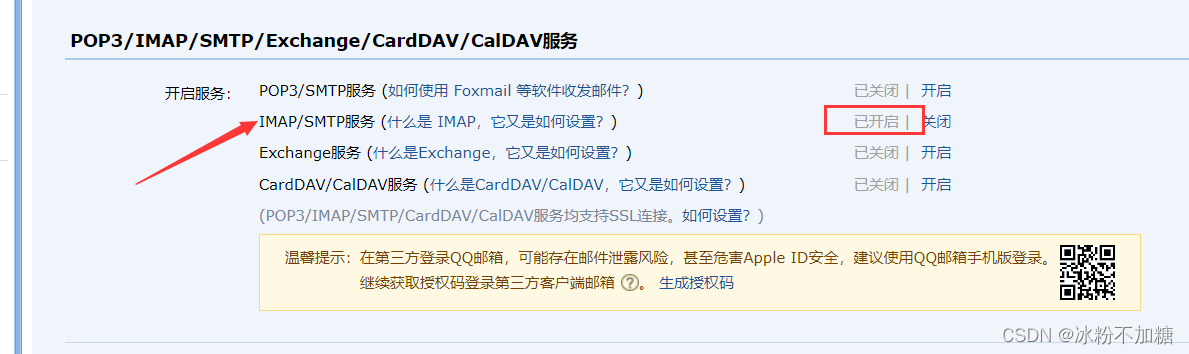
SpringBoot整合Quartz以及异步调用
文章目录前言一、异步方法调用1、导入依赖2、创建异步执行任务线程池3、创建业务层接口和实现类4、创建业务层接口和实现类二、测试定时任务1.导入依赖2.编写测试类,开启扫描定时任务3.测试三、实现定时发送邮件案例1.邮箱开启IMAP服务2.导入依赖3.导入EmailUtil4.编…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...
