动态规划-两个数组的dp问题2
文章目录
- 1. 不同的子序列(115)
- 2. 通配符匹配(44)
1. 不同的子序列(115)
题目描述:

状态表示:
根据题意这里的dp数组可以定义为二维,并且dp[i][j]表示字符串t的0到i的区间的子串在字符串s的0到j区间的子串的子序列中出现的次数也就是匹配次数。
状态转移方程:
将这里的状态分为两种情况,第一种情况就是当s的0到j这个区间的子序列不以j位置元素为结尾,那么dp[i][j]可以表示为dp[i][j]=dp[i][j-1],因为在这种情况下s的子序列不以j位置为结尾,那么直接将字符串r的指定区间内的子串和s的0到j-1区间的子序列进行匹配即可。第二种情况就是s字符串的0到j的区间内的子序列以j位置元素为结尾,那么当j位置元素与i位置元素相等时就可以得到dp[i][j]=dp[i][j],因为在此时t的子串最后一位元素已经和s的0到j区间的子序列最后一位元素相等了,那么直接去考虑前面的情况,正好前面的情况可以直接表示。在这种状态分类下,两者的结果要相加,具体看代码。
初始化:
初始化为了防止越界,给dp这个二维数组加上一行一列。然后这一行一列从逻辑上很好给他们赋值,因为加上dp的是第0行和第0列,所以逻辑上可以将其理解为s和t分别为空串的情况,当t为空串时,s中可以和其匹配只有一种可能那就是也是空串,所以第0行都赋为1。当s为空串时,其中肯定没有跟t匹配的子序列了,因此第一列直接全赋为0即可。.
然后还有一个细节问题就是字符串元素的映射,因为我们加长了数组,所以可以在字符串前面都加上一个空白字符来达到准确的字符串字符的映射。
填表顺序:
根据状态转移方程可以得到填表顺序为从上到下,从左到右。
返回值:
返回值返回dp[m][n]即可,这就是题目要求得到的结果。
代码如下:
class Solution {public int numDistinct(String s, String t) {int m = t.length();int n = s.length();int[][] dp = new int[m + 1][n + 1];for (int i = 0; i <= n; i++) {dp[0][i] = 1;}t = " " + t;s = " " + s;for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {dp[i][j] += dp[i][j - 1];if (t.charAt(i) == s.charAt(j)) {dp[i][j] += dp[i - 1][j - 1];}}}return dp[m][n];}
}
题目链接
时间复杂度:O(N^2)
空间复杂度:O(N^2)
2. 通配符匹配(44)
题目描述:

状态表示:
使用二维数组dp,使用dp[i][j]表示s在区间0-i上的子串能否和p在0-j上的子串相匹配。
状态转移方程:
对于这种两个数组的dp问题,都会对两个子串的最后一个元素进行考虑,因此这里的状态转移可以分为三种情况。第一种情况当模式串p的子串最后一个元素是一个普通的字符时,那么当s[i]==p[j]时,dp[i][j]=dp[i-1][j-1]。第二种情况当模式串的子串最后一个元素是?时,?可以匹配任何一个单个字符,所以此时的状态转移方程为dp[i][j]=dp[i-1][j-1]。第三种情况时模式串p的子串最后一个元素为*时,因为可以匹配任意个子符,所以理论上这里有很多种情况,当不匹配字符时,dp[i][j]=dp[i][j-1],当匹配一个字符时,dp[i][j]=dp[i-1][j-1],当匹配两个字符时dp[i][j]=dp[i-2][j-1]等等。
事实上第三种情况可以使用循环处理,但是效率不高,因此这里使用数学的方法对第三种情况进行优化。通过上面的分析我们知道在第三种情况下dp[i][j]=dp[i][j-1] || dp[i-1][j-1] || dp[i-2][j-1]…那么这里我们再分析dp[i-1][j]的一个状态转移方程,再第三种情况下,不难发现dp[i-1][j]=dp[i-1][j-1] || dp[i-2][j-1] || dp[i-3][j-1]…通过这两个式子的相似之处我们就可以得到dp[i][j]=dp[i][j-1] || dp[i-1][j]。
初始化:
为了避免数组越界也就是方便我们进行运算,给dp二维数组加上一行和一列,对于第一行在逻辑上的意味就是对于s子串是空串的情况下是否能够和模式串p进行匹配,模式串p的子串是空串只有在它的字符全部是*的情况下才可以成立,因此第一行我们使用一个循环来进行处理。对于第一列意味着p的子串为空串的情况,此时当然是无法匹配的,全部赋为false即可。第一行和第一列的交界处比较特殊,此时p的子串和s的子串都是空串,因此是匹配的,所以dp[0][0]赋为true。
填表顺序:
从上到下,从左至右。
返回值:
dp[m][n]。
代码如下:
class Solution {public boolean isMatch(String s, String p) {int m = s.length();int n = p.length();boolean[][] dp = new boolean[m + 1][n + 1];dp[0][0] = true;s = " " + s;p = " " + p;for (int i = 1; i <= n; i++) {if (p.charAt(i) == '*') {dp[0][i] = true;} else {break;}}for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {if (p.charAt(j) == '?') {dp[i][j] = dp[i - 1][j - 1];} else if (p.charAt(j) == '*') {if (dp[i][j - 1] || dp[i - 1][j]) {dp[i][j] = true;}} else {if (s.charAt(i) == p.charAt(j)) {dp[i][j] = dp[i - 1][j - 1];}}}}return dp[m][n];}
}
题目链接
时间复杂度:O(N^2)
空间复杂度:O(N^2)
相关文章:

动态规划-两个数组的dp问题2
文章目录 1. 不同的子序列(115)2. 通配符匹配(44) 1. 不同的子序列(115) 题目描述: 状态表示: 根据题意这里的dp数组可以定义为二维,并且dp[i][j]表示字符串t的0到i的…...

如何设置并行度 ——《OceanBase 并行执行》系列 2
并行度(degree of parallelism,简称 DOP),是指在执行过程中所使用的工作线程数量。设计并行执行的初衷在于充分利用多核资源以提升效率。OceanBase 的并行执行框架支持多种设定并行度的方式,既允许用户手动设置&#x…...
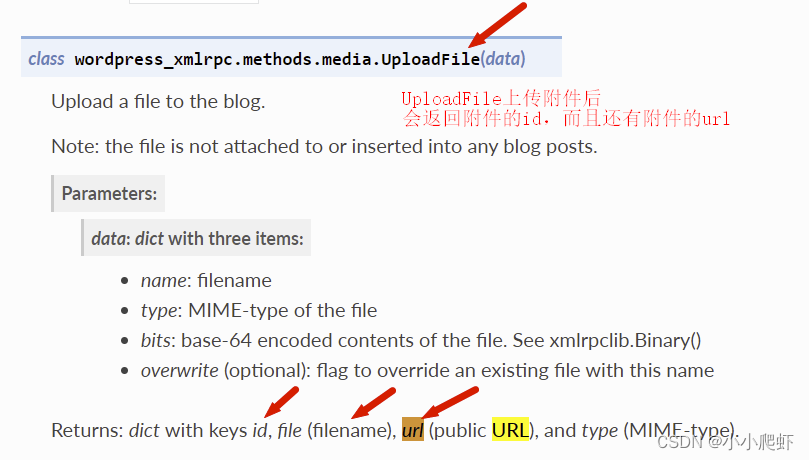
python直接发布到网站wordpress之三批量发布图片
在前面的文章中,实现了使用python操作wordpress发布文字内容和图片内容。 python直接发布到网站wordpress之一只发布文字-CSDN博客 python直接发布到网站wordpress之二发布图片-CSDN博客 不过,此时发布图片的数量只能是一张图片。但在实际应用中&…...

C#面:ADO.NET 相对于ADO等主要有什么改进
C# ADO.NET 是微软为.NET平台开发的一套数据访问技术,相对于传统的ADO(ActiveX Data Objects)等,它有以下几个主要改进: 面向对象:ADO.NET 是面向对象的数据访问技术,它使用.NET框架中的类和对…...
web前端学习笔记7-iconfont使用
7. iconfont的使用流程 字体图标使用较多的是阿里巴巴iconfont图标库,它是阿里巴巴体验团队推出的图标库和图标管理平台,提供了大量免费和可定制的矢量图标,以满足网页设计、平面设计、UI设计、应用程序开发和其他创意项目的需求。 官方网站:https://www.iconfont.cn/ 使用…...
国内小白用什么方法充值使用ChatGPT4.0?
首先说一下IOS礼品卡订阅,目前最经济实惠的订阅方式,具体操作步骤 使用IOS设备充值,用 App Stroe 兑换券 1、支付宝地址切换旧金山,在里面买app store 的兑换卷 2、美区Apple ID登陆app store ,充值兑换券 3、IOS设…...

富格林:正确杜绝欺诈实现出金
富格林悉知,现货黄金一直以来都是投资者们追逐的热门品种之一。其安全性和避险特性吸引着广大投资者。但在现货黄金市场中要想实现出金其实并不简单,是需要我们通过一定的技巧和方法去正确杜绝欺诈套路。下面为了帮助广大投资者正确杜绝欺诈实现出金&…...
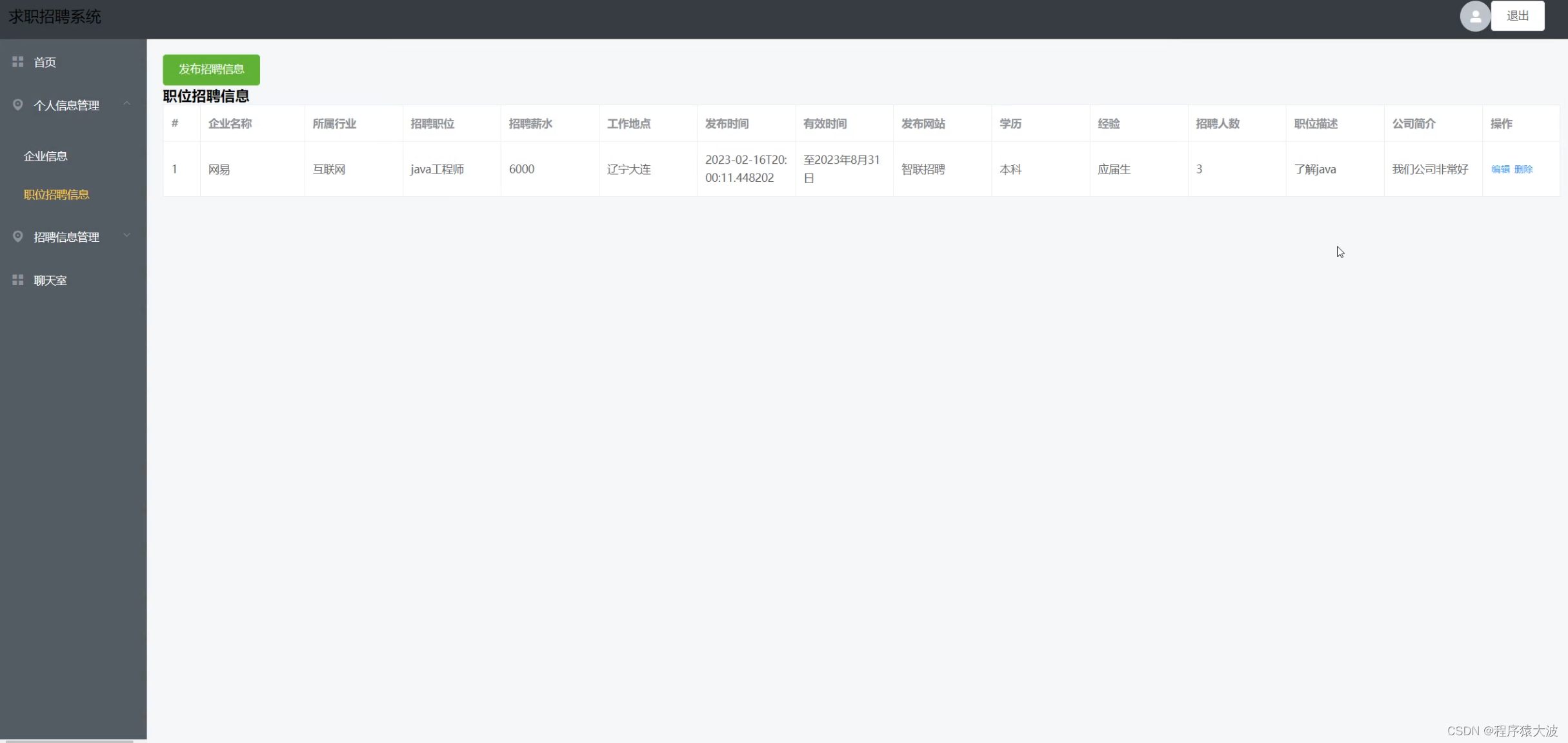
基于java,SpringBoot和VUE的求职招聘简历管理系统设计
摘要 基于Java, Spring Boot和Vue的求职招聘管理系统是一个为了简化求职者与雇主间互动流程而设计的现代化在线平台。该系统后端采用Spring Boot框架,以便快速搭建具有自动配置、安全性和事务管理等特性的RESTful API服务,而前端则使用Vue.js框架构建动…...

sqlserver数据库日志文件log.ldf文件占用过大清除的办法
sqlserver数据库日志文件log.ldf文件占用过大清除的办法 技术交流 http://idea.coderyj.com/ 1.清除数据库日志的方法 --- 查看数据库日志文件名 USE cs GO SELECT file_id, name,size,* FROM sys.database_files;ps 可以看到其中name字段为数据库日志名称"数据库日志名称…...

【Python小技巧】matplotlib不显示图像竟是numpy惹的祸
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、问题:df.plot() 显示不出图像二、尝试各种解决办法1. 增加matplotlib.use,设定GUI2. 升级matplotlib版本 三、numpy是个重要的库1. …...

【AIGC】1、爆火的 AIGC 到底是什么 | 全面介绍
文章目录 一、AIGC 的简要介绍二、AIGC 的发展历程三、AIGC 的基石3.1 基本模型3.2 基于人类反馈的强化学习3.3 算力支持 四、生成式 AI(Generative AI)4.1 单模态4.1.1 生成式语言模型(Generative Language Models,GLM࿰…...

云计算技术概述_3.云计算的部署方式
根据NIST的定义,云计算从部署模式上看可以分为公有云、社区云、私有云和混合云四种类型。 注:NIST(美国国家标准与技术研究院)是美国商务部下属的一个物理科学实验室和非监管机构。 其任务是促进创新和行业竞争力。 NIST 将其活动…...
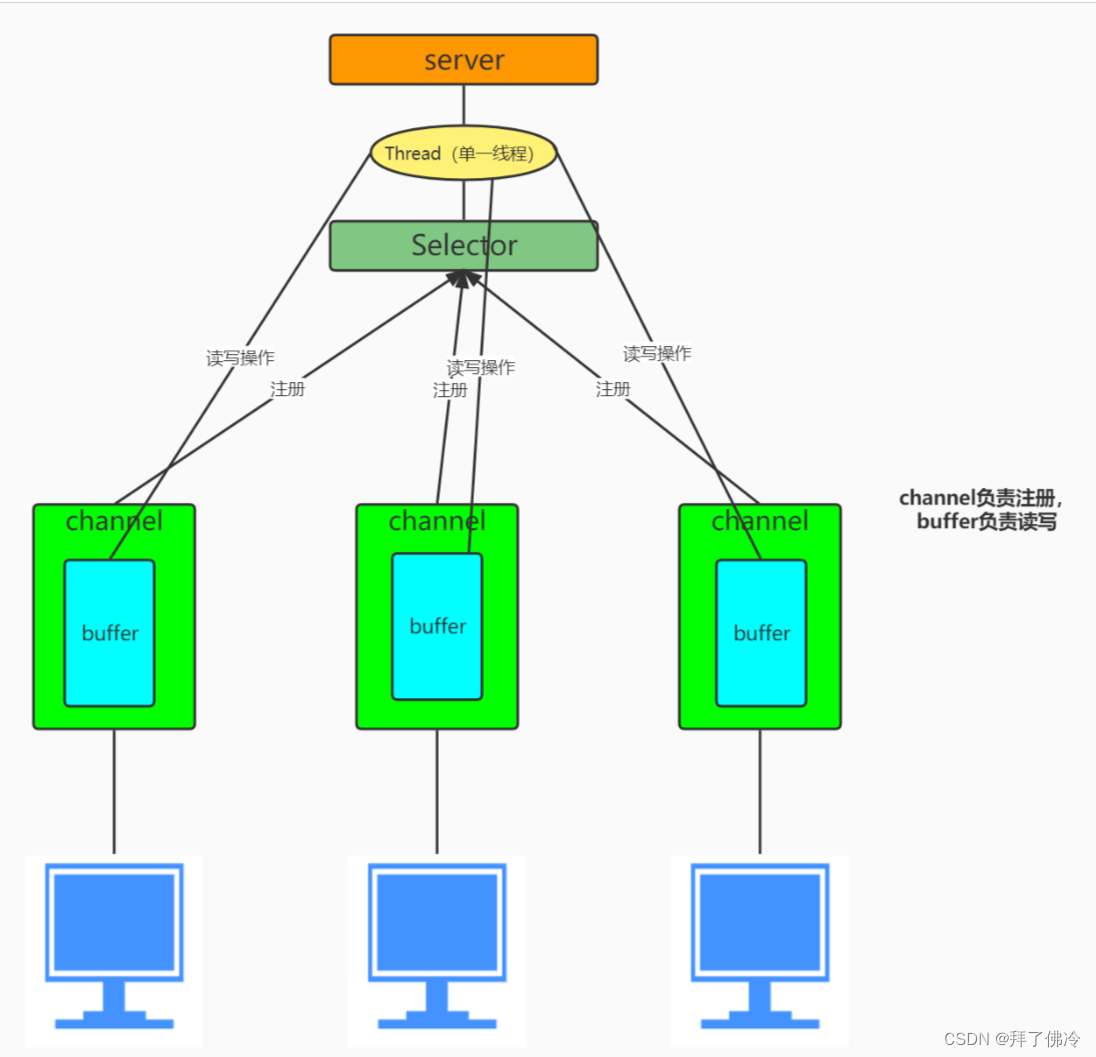
简述 BIO 、NIO 模型
BIO : 同步阻塞I/O(Block IO) 服务器实现模式为每一个连接一个线程,即客户端有连接请求时服务器就需要启动一个线程进行处理,如果这个连接不做任何事情会造成不必要的线程开销,此处可以通过线程池机制进行优化。 impo…...

【Python小练】随机验证码
题目 提示输出含数字、字母的四位随机数,输入提示的验证码进行验证,验证码正确结束程序,验证码错误继续输入。 分析 我们可以通过random模块生成0到9的随机数,也可以通过生成65到90的随机数,将65到90的随机ASCLL码转换…...

《1w实盘and大盘基金预测 day30》
今日预测: 3123-3150-3177 探底回升,震荡上涨,收小红小绿 双创指数后期上涨的幅度也是会大于上证的,四月底的时候就提醒建仓。 关注板块:医疗、地产、电力、证券 这周预测 这周上证指数最高看到3200 继续看涨&#…...
软件工程案例学习-图书管理系统-面向对象方法
文档编号:LMS_1 版 本 号:V1.0 ** ** ** ** ** ** 文档名称:需求分析规格说明书 项目名称:图书管理系统 项目负责人:计敏 胡杰 ** ** …...
)
python:机器学习特征优选(过滤法)
作者:CSDN @ _养乐多_ 本文将介绍如何使用 python 语言使用过滤法进行机器学习特征优选。分别有F值、互信息(Mutual Information,MI)、方差阈值(Variance Threshold,VT)、相关性方法。 文章目录 一、特征数据1.1 将用于分析的数据从GEE下载到本地1.2 从其他方法获取二、…...

CH32V 系列 MCU IAP 使用函数形式通过传参形式灵活指定APP跳转地址
参考: CH32V 系列 MCU IAP 升级跳转方法 CH32V103 的 IAP 问题(跳转及中断向量表重定位) 1. 沁恒的RISC-V内核MCU的IAP跳转示例程序简要分析 沁恒的RISC-V内核的MCU比如CH32V203、CH32V307等系列的EVT包中IAP升级的示例程序中都是通过使能软件中断之后&…...

教程分享:如何为跨境电商、外贸、国际展会制作二维码?
不论是做跨境电商、在全球做产品推广,还是国外的餐厅运营、参加国际展会,或者是做创意户外广告、制作个性化的个人名片、有趣的产品包装……只要是在国外使用二维码,你都可以在QR Tiger去制作您需要的二维码! 一、认识QR Tiger 二…...
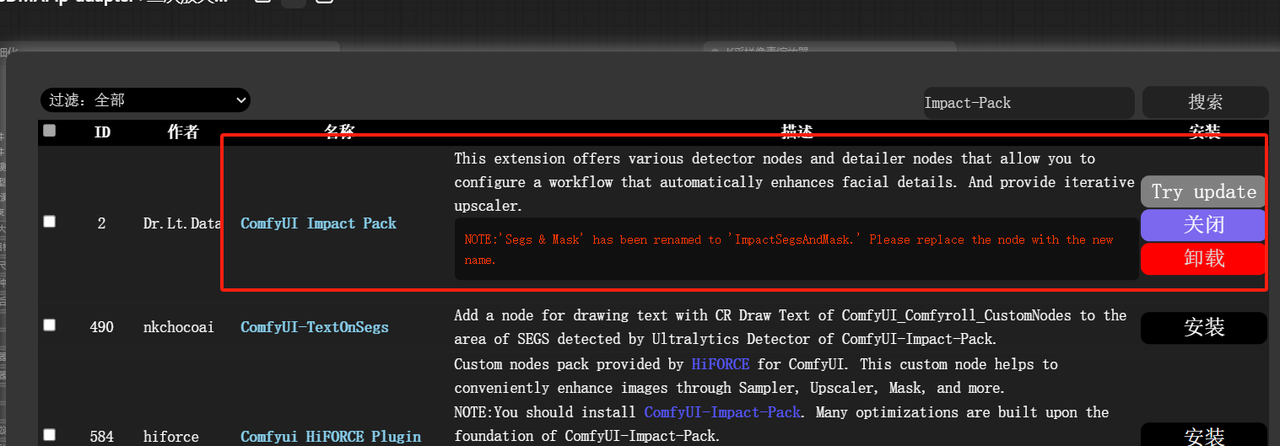
ComfyUI 基础教程(十三):ComfyUI-Impact-Pack 面部修复
SD的WebUI 中的面部修复神器 ADetailer,无法在ComfyUI 中使用。那么如何在ComfyUI中进行面部处理呢?ComfyUI 中也有几个面部修复功能,比如ComfyUI Impact Pack(FaceDetailer),以及换脸插件Reactor和IPAdapter。 ComfyUI-Impact-Pack 是一个功能强大的插件,专为 ComfyUI …...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...
