高级数据结构与算法习题(9)
一、判断题
1、Let S be the set of activities in Activity Selection Problem. Then the earliest finish activity am must be included in all the maximum-size subset of mutually compatible activities of S.
T F
解析:F。设S是活动选择问题中的一组活动。那么,S的相互兼容活动必须有一些最大大小的子集,其中包括最早完成的活动am。但是并不是最早完成活动am必须包括在S的所有相互兼容活动的最大规模子集中。
2、Let C be an alphabet in which each character c in C has frequency c.freq. If the size of C is n, the length of the optimal prefix code for any character c is not greater than n−1.
T F
解析:T。根据哈夫曼树的性质,对于字符集大小为 n 的情况,任何一个字符的最优编码长度不会超过 n-1。这是因为在哈夫曼树中,从根节点到叶子节点的路径长度即为该字符的编码长度,而哈夫曼树的最短路径长度为 1,最长路径长度为 n-1。
二、单选题
Consider the problem of making change for n cents using the fewest number of coins. Assume that each coin's value is an integer.
The coins of the lowest denomination(面额) is the cent.
(I) Suppose that the available coins are quarters (25 cents), dimes (10 cents), nickels (5 cents), and pennies (1 cent). The greedy algorithm always yields an optimal solution.
(II) Suppose that the available coins are in the denominations that are powers of c, that is, the denominations are for some integers
and
. The greedy algorithm always yields an optimal solution.
(III) Given any set of k different coin denominations which includes a penny (1 cent) so that there is a solution for every value of n, greedy algorithm always yields an optimal solution.
Which of the following is correct?
A.Statement (I) is false.
B.Statement (II) is false.
C.Statement (III) is false.
D.All of the three statements are correct.
解析:A。贪心算法有时候算出的结果并不是
相关文章:
高级数据结构与算法习题(9)
一、判断题 1、Let S be the set of activities in Activity Selection Problem. Then the earliest finish activity am must be included in all the maximum-size subset of mutually compatible activities of S. T F 解析:F。设S是活动选择问题中的一…...

Linux的vim下制作进度条
目录 前言: 回车和换行有区别吗? 回车和换行的区别展示(这个我在Linux下演示) 为什么会消失呢? 回车和换行的区别 为什么\r和\n产生的效果不同? 打印进度条: (1)打印字符串 …...

C++学习笔记2
T1 奇怪的教室 题目背景 LSU 的老师有个奇怪的教室,同学们会从左到右坐成一个横排,并且同一个位置可以坐多个同学。这天,入学考试的成绩下来了。同学们想根据入学考试的成绩,找出班里学霸扎堆的区域“学霸区”。 题目描述 共有…...

细数:智能物流装备界的并购案~
导语 大家好,我是智能仓储物流技术研习社的社长,老K。专注分享智能仓储物流技术、智能制造等内容。 新书《智能物流系统构成与技术实践》 近年来,随着智能仓储物流行业的快速发展,全球范围内的并购活动日益频繁,各大企…...

微信小程序播放编码为 video/mp4;codecs=vp8 opus 的视频没有声音
最近在做浏览器录屏功能,主要是录屏加上麦克风生成mp4视频,最终生成的是编码为 video/mp4;codecsvp8 opus 的视频,音频编码因为是 opus 是无法在小程序正常播放的,这样就导致了视频没有声音。后来就在服务端做了一层转换ÿ…...

Linux 指令lsblk 作用,以及查看cpu使用情况和磁盘IO iostat指令详解
lsblk 指令 在Linux系统中,lsblk(列表块设备)命令是一个非常实用的工具,用于显示所有可用的块设备信息,如硬盘、USB驱动器、SD卡以及它们的分区。这个命令以易于理解的树状结构展示这些信息,清晰地表明了设…...
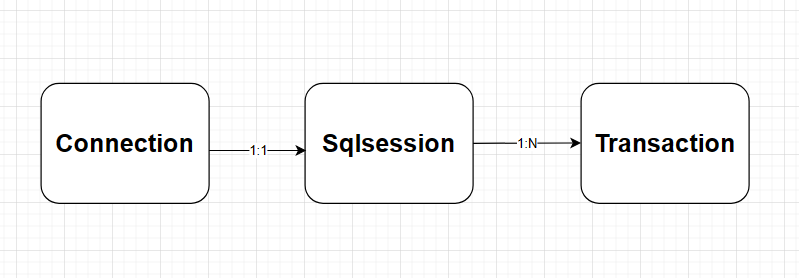
Mybatis之Sqlsession、Connection和Transaction三者间的关系
前言 最近在看Mybatis的源码,搜到这篇文章Sqlsession、Connection和Transaction原理与三者间的关系,debug之后发现有不少疑惑,于是按照原文整理了一下,记录下debug中的一些困惑点。 对于我们开发来讲,不管跟任何关系…...
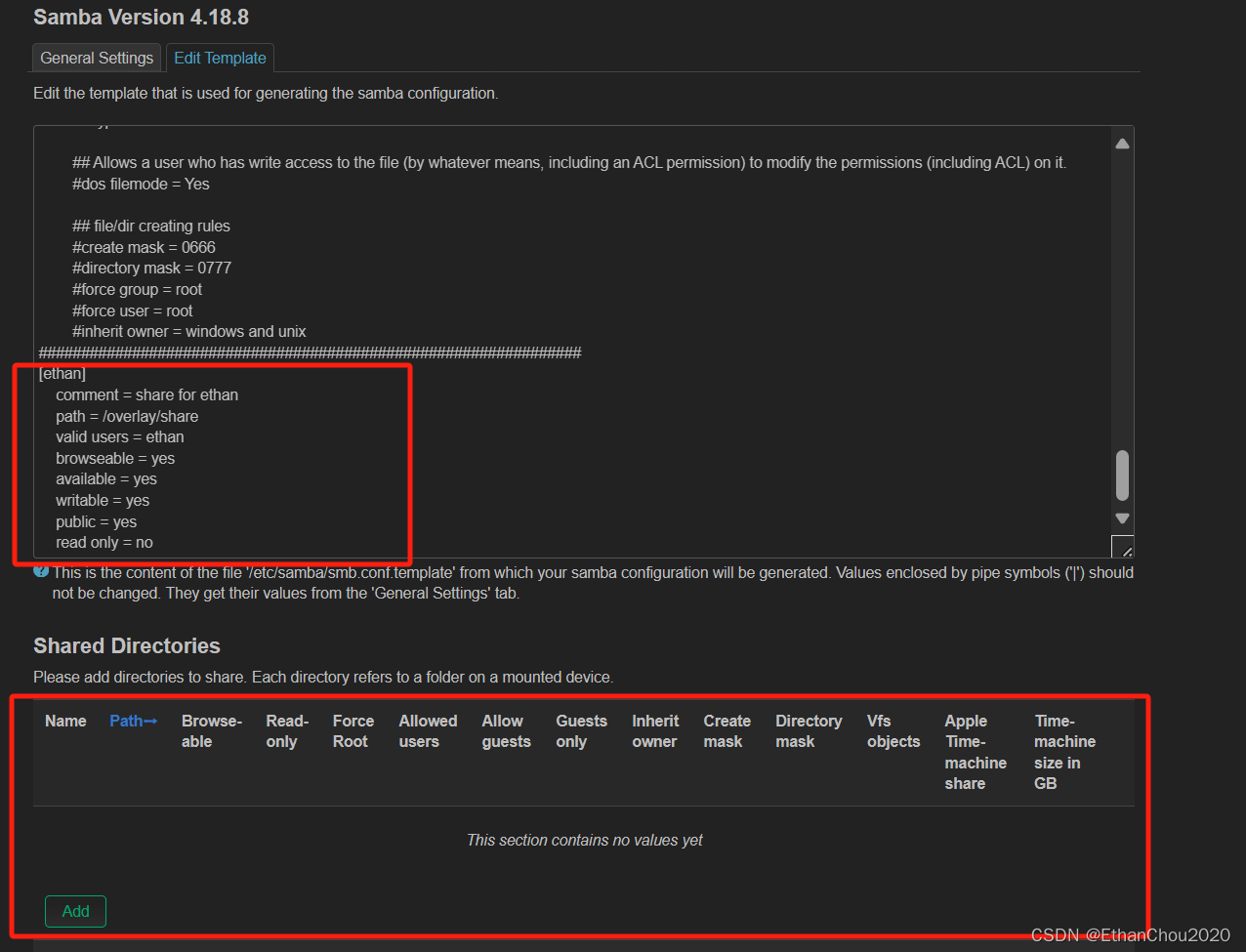
WRT1900ACS搭建openwrt服务器小记
参考链接 wrt1900acs openwrt wrt1900acs openwrt 刷机 wrt1900acs原生固件刷openwrt-23.05.3-mvebu-cortexa9-linksys_wrt1900acs-squashfs-factory.img wrt1900acs openwrt更新刷openwrt-23.05.3-mvebu-cortexa9-linksys_wrt1900acs-squashfs-sysupgrade.bin 通过WEB UI来…...
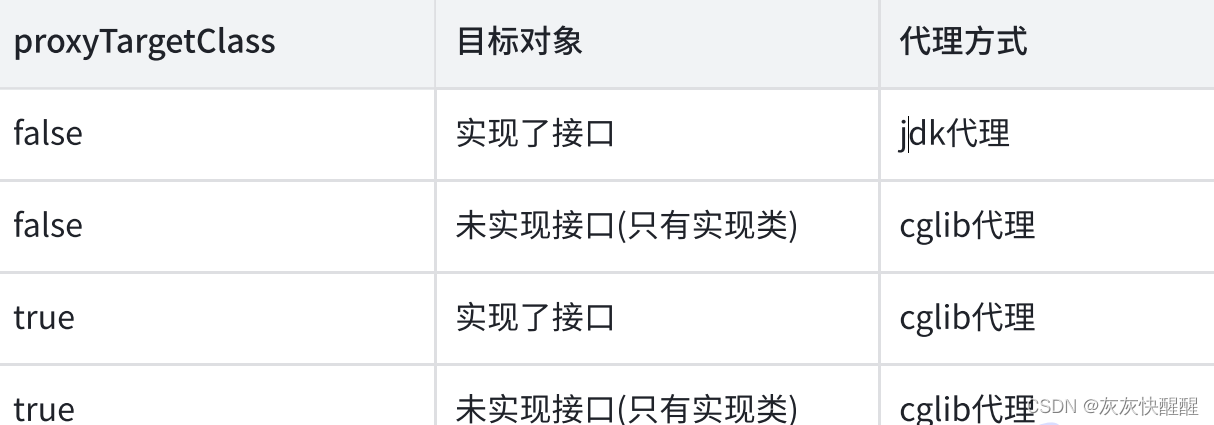
Spring AOP(3)
目录 Spring AOP原理 代理模式 代理模式中的主要角色 静态代理 动态代理 总结:面试题 什么是AOP? Spring AOP实现的方式有哪些? Spring AOP实现原理 Spring使用的是哪种代理方式? JDK和CGLIB动态代理的区别? Spring AOP原理 代理模式 代理模式, 也叫委托模式. …...
推荐5个免费的国内平替版GPT
提起AI,大家第一个想到的就是GPT。 虽然它确实很厉害,但奈何于我们水土不服,使用门槛有些高。 不过随着GPT的爆火,现在AI智能工具已经遍布到各行各业了,随着时间的推移,国内的AI工具也已经“百花盛放”了…...

弹性云服务器是什么,为何如此受欢迎
云计算作为当下炙手可热的技术领域,已然成为现代企业不可或缺的核心能力。云服务器作为云计算的基石之一,在这个数字化时代发挥着至关重要的作用。而弹性云服务器,作为云服务器的一种演进形式,更是备受瞩目。 弹性云服务器&#…...
Docker部署RabbitMQ与简单使用
官网地址: Messaging that just works — RabbitMQ 我的Docker博客:Docker-CSDN博客 1.结构 其中包含几个概念: **publisher**:生产者,也就是发送消息的一方 **consumer**:消费者,也就是消费消息的一方 …...

2024年黄石市建设优质工程评价认定申报条件、流程及材料合集
2024年黄石市建设优质工程评价认定申报条件、流程及材料合集如下,黄石市的企业单位可以了解一下,有疑问名字找我哦。 第一章总则 第一条为贯彻落实《中华人民共和国建筑法》、《安全生产法》、《建设工程质量管理条例》、《建设工程安全生产管理条例》…...
偏微分方程算法之混合边界条件下的差分法
目录 一、研究目标 二、理论推导 三、算例实现 四、结论 一、研究目标 我们在前几节中介绍了Poisson方程的边值问题,接下来对椭圆型偏微分方程的混合边值问题进行探讨,研究对象为: 其中,为矩形区域,为上的连续函数…...
apollo资料整理
Application X: Application X Apollo: Apollo 自动驾驶开放平台 Cyber RT API tutorial — Cyber RT Documents documentation Cyber RT API tutorial — Cyber RT Documents documentation GitHub - daohu527/dig-into-apollo: Apollo notes (Apollo学习笔记) - Apollo l…...

森林消防新利器:高扬程水泵的革新与应用/恒峰智慧科技
随着全球气候变化的加剧,森林火灾的频发已成为威胁生态安全的重要问题。在森林消防工作中,高效、快速的水源供给设备显得尤为重要。近年来,高扬程水泵的广泛应用,为森林消防工作带来了新的希望与突破。 一、高扬程水泵的技术优势 …...
Microsoft Universal Print 与 SAP 集成教程
引言 从 SAP 环境打印是许多客户的要求。例如数据列表打印、批量打印或标签打印。此类生产和批量打印方案通常使用专用硬件、驱动程序和打印解决方案来解决。 Microsoft Universal Print 是一种基于云的打印解决方案,它允许组织以集中化的方式管理打印机和打印机驱…...
VBA在Excel中字母、数字的相互转化
VBA在Excel中字母、数字的相互转化 字母转数字的方法 数字转字母的方法 众所周知,Excel表中的行以数字展示,列用字母展示,如下图: 编程时,很多时候需要将列的字母转变为数字使用,如cells(num1,num2).value等,不知大家是怎么将字母转化为数字的,Excel是否有其他方式…...

【C语言】——联合体与枚举
【C语言】——联合体与枚举 一、联合体1.1、联合体类型的声明1.2、联合体的特点1.3、相同成员的结构体和联合体对比1.4、联合体的大小计算1.5、联合体的应用举例 二、枚举2.1、枚举类型的声明2.2、枚举类型的优点 一、联合体 1.1、联合体类型的声明 联合体也叫做共用体 与…...
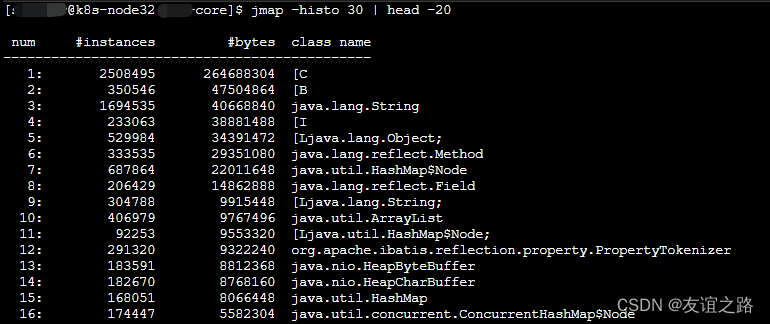
java线上问题排查之内存分析(三)
java线上问题排查之内存分析 使用top命令 top命令显示的结果列表中,会看到%MEM这一列,这里可以看到你的进程可能对内存的使用率特别高。以查看正在运行的进程和系统负载信息,包括cpu负载、内存使用、各个进程所占系统资源等。 2.用jstat命令…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...
