vue+element-ui实现横向长箭头,横向线上下可自定义文字(使用after伪元素实现箭头)
项目场景:
需要实现一个长箭头,横向线上下可自定义文字
代码描述
<div><span class="data-model">{{ //上方文字}}</span><el-divider class="q"> </el-divider>//分隔线<span class="data-model">{{//下方文字}}</span></div>
<style>.data-model {display: inline-block;width: 100%;text-align: center;}.el-divider {position: relative;margin: 8px 0;background: #4162ff;}.el-divider::after {content: '>';position: absolute;right: 12px;top: 0;transform: translateY(-52%);width: 0;color: #4162ff;font-size: 22px;}
</style>
实现效果:

相关文章:

vue+element-ui实现横向长箭头,横向线上下可自定义文字(使用after伪元素实现箭头)
项目场景: 需要实现一个长箭头,横向线上下可自定义文字 代码描述 <div><span class"data-model">{{ //上方文字}}</span><el-divider class"q"> </el-divider>//分隔线<span class"data-mod…...
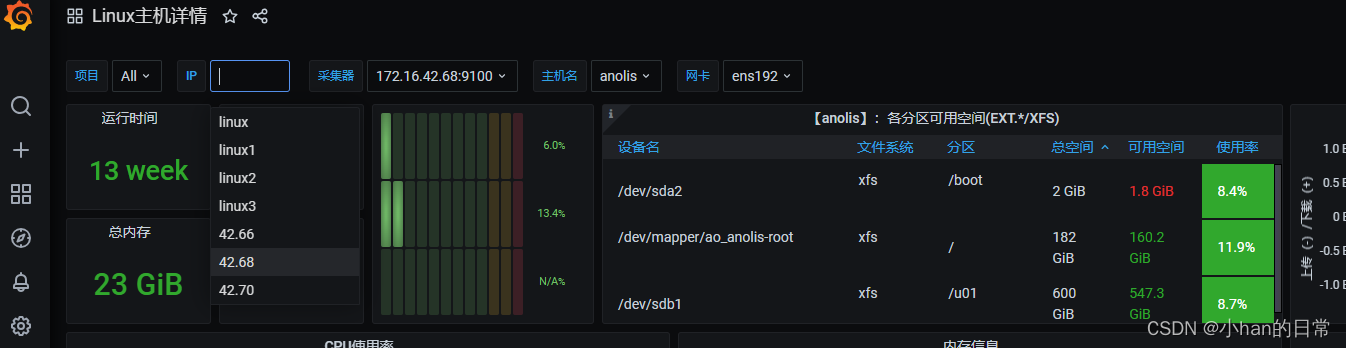
性能监控之prometheus+grafana搭建
前言 Prometheus和Grafana是两个流行的开源工具,用于监控和可视化系统和应用程序的性能指标。它们通常一起使用,提供了强大的监控和数据可视化功能。 Prometheus Prometheus是一种开源的系统监控和警报工具包。它最初由SoundCloud开发,并于…...
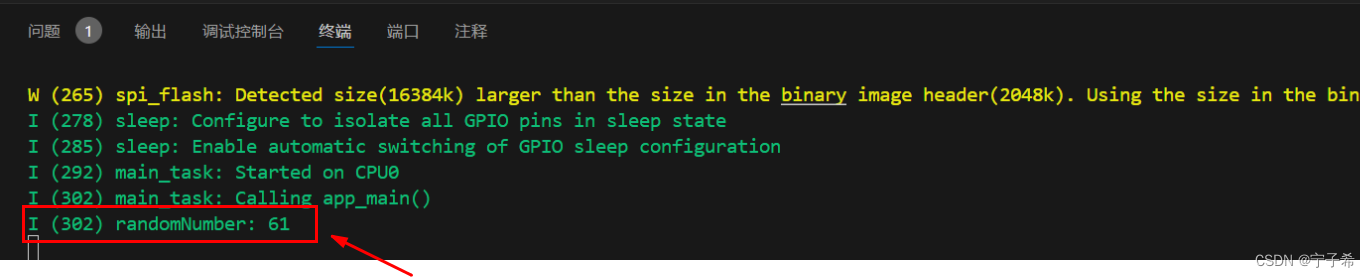
25-ESP32-S3 内置的真随机数发生器(RNG)
ESP32-S3 内置的真随机数发生器(RNG)😎 引言 📚 在许多应用中,随机数发生器(RNG)是必不可少的。无论是在密码学🔒、游戏🎮、模拟🧪或其他领域,随…...

万兆以太网MAC设计(12)万兆UDP协议栈上板与主机网卡通信
文章目录 一、设置IP以及MAC二、上板效果2.1、板卡与主机数据回环测试2.2、板卡满带宽发送数据 一、设置IP以及MAC 顶层模块设置源MAC地址 module XC7Z100_Top#(parameter P_SRC_MAC 48h01_02_03_04_05_06,parameter P_DST_MAC 48hff_ff_ff_ff_ff_ff )(input …...

2024年4月17日华为春招实习试题【三题】-题目+题解+在线评测,2024.4.17,华为机试
2024年4月17日华为春招实习试题【三题】-题目题解在线评测 🔮题目一描述:扑克牌消消乐输入描述输出描述样例一样例二Limitation解题思路一:模拟,遇到连续3张相同牌号的卡牌,直接删除解题思路二:栈解题思路三…...
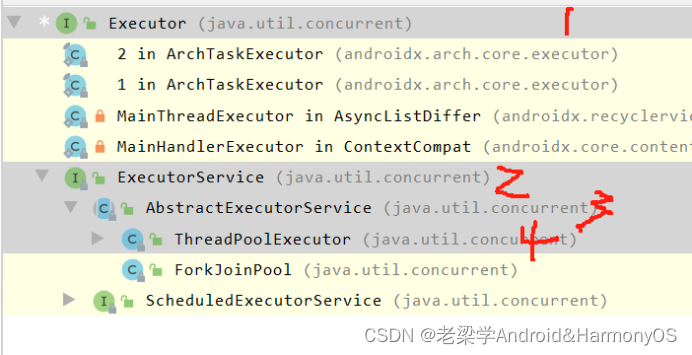
展开说说:Android线程池解析
何谓线程池?本人理解是存放和管理线程的一个容器。 线程池存在的意义是什么? 第一:前面博客提到过创建和销毁线程的操作本身是有性能开销的,如果把使用的线程对象存起来下次用的时候直接取出来用就省去了一次创建和销毁的成本&a…...

Selenium自动化测试面试题全家桶
🔥 交流讨论:欢迎加入我们一起学习! 🔥 资源分享:耗时200小时精选的「软件测试」资料包 🔥 教程推荐:火遍全网的《软件测试》教程 📢欢迎点赞 👍 收藏 ⭐留言 …...

Docker 容器日志占用空间过大解决办法
1、vi /etc/docker/daemon.json {"log-driver":"json-file","log-opts": {"max-size":"200m", "max-file":"1"} } 2、重新加载守护进程配置文件 systemctl daemon-reload 3、重启docker systemctl…...

update_min_vruntime()流程图
linux kernel scheduler cfs的update_min_vruntime() 看起来还挺绕的。含义其实也简单,总一句话,将 cfs_rq->min_vruntime 设置为: max( cfs_rq->vruntime, min(leftmost_se->vruntime, cfs_rq->curr->vruntime) )。 画个流…...
)
十进制转任意进制(以及任意进制来回转换<了解>)
十进制转任意进制: #include <iostream> #include <vector> #include <string> using namespace std; // 将十进制数转换为P进制形式的字符串 string toBase(int num, int base) {string result ""; // 初始化结果字符串为空wh…...

postcss-px-to-viewport 从入坑到放弃 (nuxt3搭建响应式官网解决方案 )
前沿 什么是 postcss-px-to-viewport 将px单位转换为视口单位的 (vw, vh, vmin, vmax) 的 PostCSS 插件。 为什么使用 postcss-px-to-viewport 在pc端盛行的时代 ,如果你不想去适配更多的pc端代码,可以采用它。 由于nuxt3本身已带postcss,所…...

C语言从入门到入门
一、引言 C语言是一种通用的、过程式的计算机编程语言,支持结构化编程、词汇变量作用域和递归等功能,其设计提供了低级别的存取权限,并且要求程序员管理所有的内存细节。C语言具有高效、灵活和可移植性等特点,因此被广泛应用于系统编程、嵌入式系统开发、游戏开发等领域。 …...

Java基础教程 - 4 流程控制
更好的阅读体验:点这里 ( www.doubibiji.com ) 更好的阅读体验:点这里 ( www.doubibiji.com ) 更好的阅读体验:点这里 ( www.doubibiji.com ) 4 流程控制 4.1 分支结构…...
的方式?)
大厂Java面试题:MyBatis中有几种加载映射器(Mapper.xml)的方式?
大家好,我是王有志。 今天给大家带来的是一道来自京东的 MyBatis 面试题:MyBatis 中有几种加载映射器(Mapper.xml)的方式? 常见加载 MyBatis 映射器的方式有 5 种,可以根据不同的使用方式来进行具体区分&…...
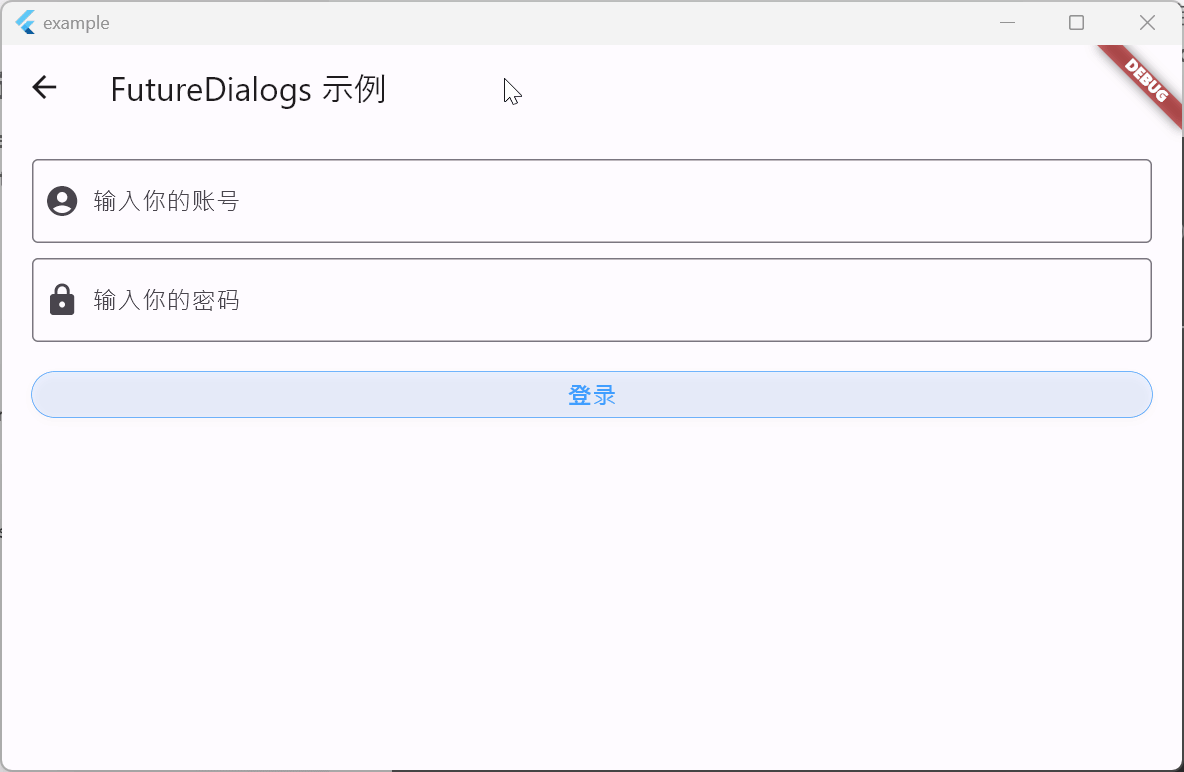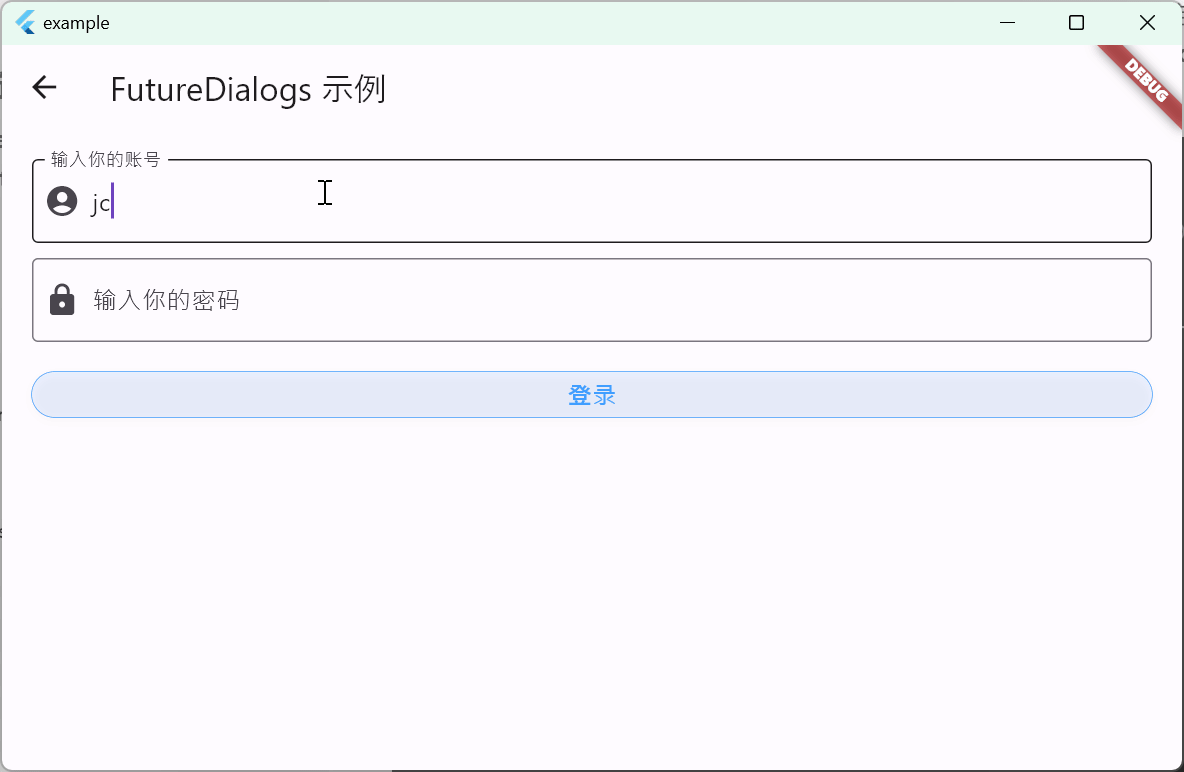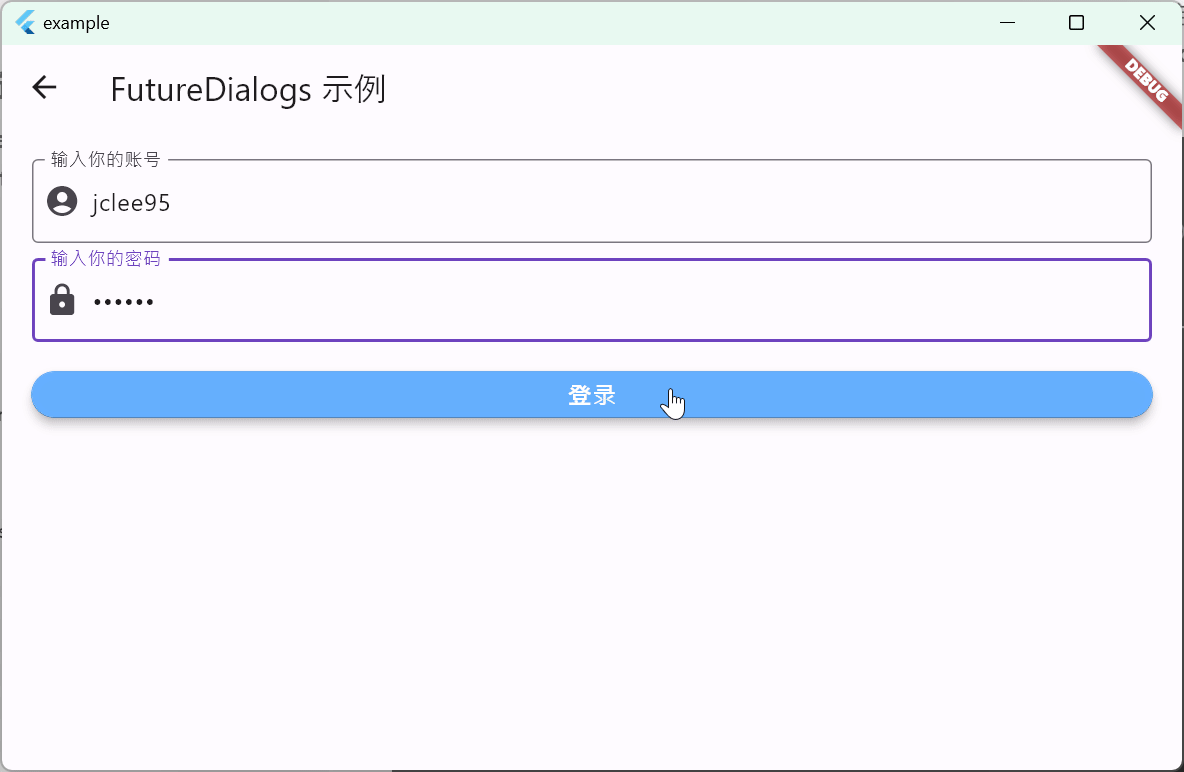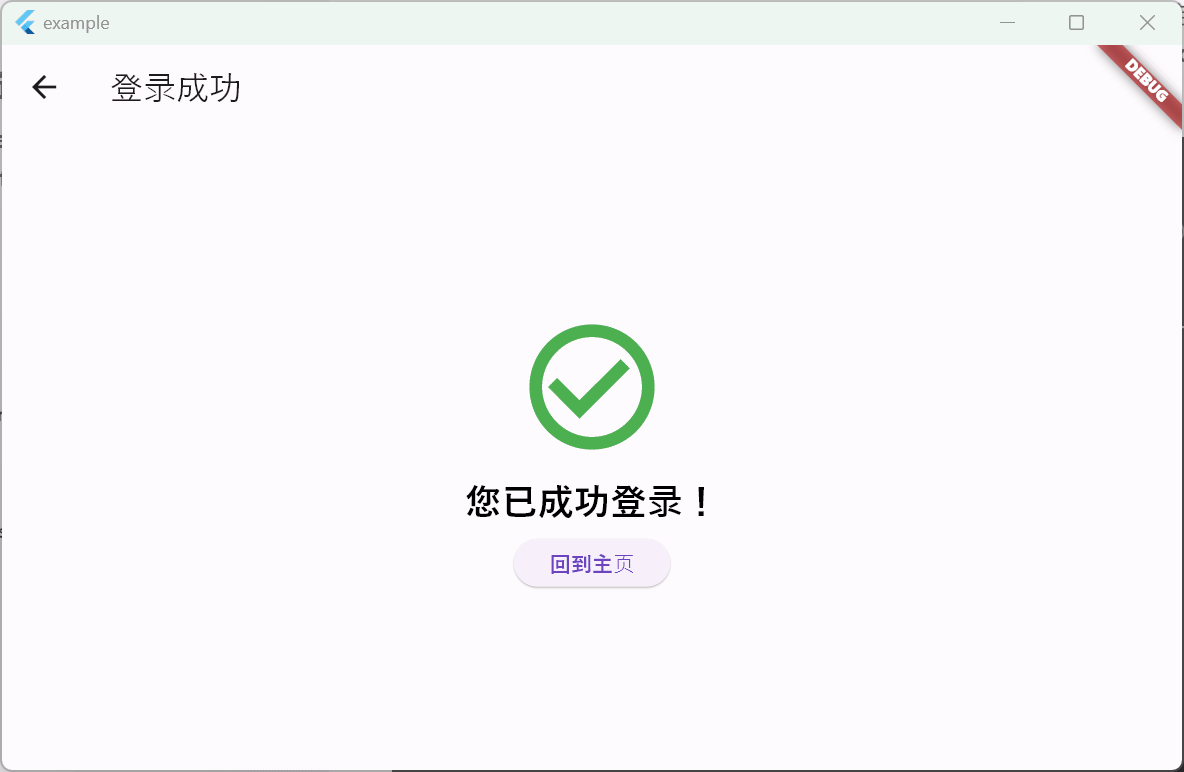
Flutter笔记:Widgets Easier组件库(10)快速处理承若型对话
Flutter笔记 使用Widgets Easier组件库快速处理承若型对话 - 文章信息 - Author: 李俊才 (jcLee95) Visit me at CSDN: https://jclee95.blog.csdn.netMy WebSite:http://thispage.tech/Email: 291148484163.com. Shenzhen ChinaAddress of this article:https://…...

10_Linux中的计划任务
10_Linux中的计划任务 常见计划任务 Linux系统中默认在执行的计划任务 日志文件的轮询:logrotate日志文件分析logwatch任务建立locate数据库建立manpage查询数据库RPM软件日志文件删除缓存与网络有关的分析 仅执行一次的计划任务 atd和at [rootnode4 ~]# systemctl start…...

Google Play开发者账号为什么会被封?如何解决关联账号问题?
Google Play是Google提供的一个应用商店,用户可以在其中下载并安装Android设备上的应用程序、电影、音乐、电子图书等。Google Play是Android平台上较大的应用市场,包含了数百万个应用程序和游戏。但是谷歌对于上架应用的审核越趋严格,开发者…...
【leetcode题解】151、反转字符串中的单词)
(第12天)【leetcode题解】151、反转字符串中的单词
目录 151、反转字符串中的单词题目描述思路代码本题反思 151、反转字符串中的单词 题目描述 给你一个字符串 s ,请你反转字符串中单词的顺序。 单词是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的单词分隔开。 返回单词顺序颠倒且单词之间用单个…...
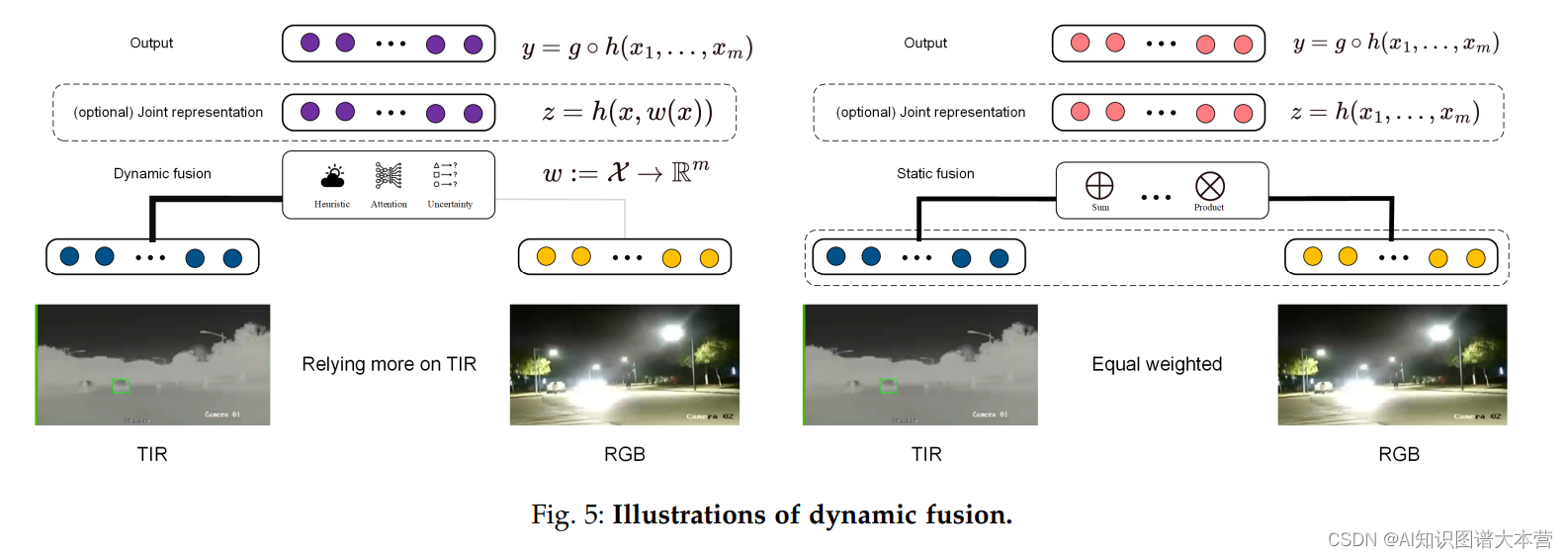
如何处理多模态数据噪声不均衡动态?天大等最新《低质量数据的多模态融合》综述
多模态融合致力于整合来自多种模态的信息,目的是实现更准确的预测。在包括自动驾驶和医疗诊断等广泛的场景中,多模态融合已取得显著进展。然而,在低质量数据环境下,多模态融合的可靠性大部分仍未被探索。本文综述了开放多模态融合…...
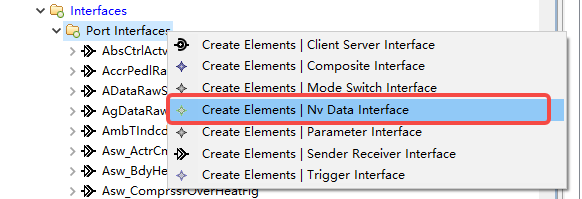
Autosar NvM配置-手动配置Nvblock及使用-基于ETAS软件
文章目录 前言NvDataInterfaceNvBlockNvM配置SWC配置RTE Mapping使用生成的接口操作NVM总结前言 NVM作为存储协议栈中最顶层的模块,是必须要掌握的。目前项目基本使用MCU带的Dflash模块,使用Fee模拟eeprom。在项目前期阶段,应该充分讨论需要存储的内容,包括应用数据,诊断…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...
