python Django 的内置权限系统或自定义模型来存储更复杂的角色和权限关系
在 Django 中,管理用户权限和角色通常涉及到使用 Django 的内置权限系统或自定义模型来存储更复杂的角色和权限关系。下面是一个基本的指南,说明如何在 Django 中为后台管理系统分配权限并将其保存在数据库中,同时结合 Vue.js 和 Element UI 作为前端框架。
后端(Django)
使用 Django 的内置用户模型(User)和权限模型(Permission):
Django 提供了内置的 User 和 Permission 模型来管理用户权限。你可以通过 Django 的管理界面或自定义视图来为用户分配权限。
自定义角色模型(如果需要):
如果你的权限系统需要更复杂的角色管理,你可以创建自定义的 Role 模型,并通过 ManyToManyField 与 Permission 模型关联。这样,你可以将多个权限分配给一个角色,然后将角色分配给用户。
python 复制
from django.db import models
from django.contrib.auth.models import Permission
class Role(models.Model):
name = models.CharField(max_length=255)
permissions = models.ManyToManyField(Permission, blank=True)
def __str__(self):
return self.name
# 还需要在 `User` 模型中添加与 `Role` 的关联,例如通过 Profile 模型
创建视图来处理权限分配:
相关文章:

python Django 的内置权限系统或自定义模型来存储更复杂的角色和权限关系
在 Django 中,管理用户权限和角色通常涉及到使用 Django 的内置权限系统或自定义模型来存储更复杂的角色和权限关系。下面是一个基本的指南,说明如何在 Django 中为后台管理系统分配权限并将其保存在数据库中,同时结合 Vue.js 和 Element UI 作为前端框架。 后端(Django)…...

不上班,我靠这5份赚钱副业养活了自己
在这个快节奏的社会里,很多人都在为生活奔波忙碌。今天,就让我来跟大家分享一下我的“躺平”秘籍吧! 这一个月来,我没有上班,但好在有副业养活自己。有时候,我真的觉得有一份自己喜欢的自媒体副业挺好的。…...
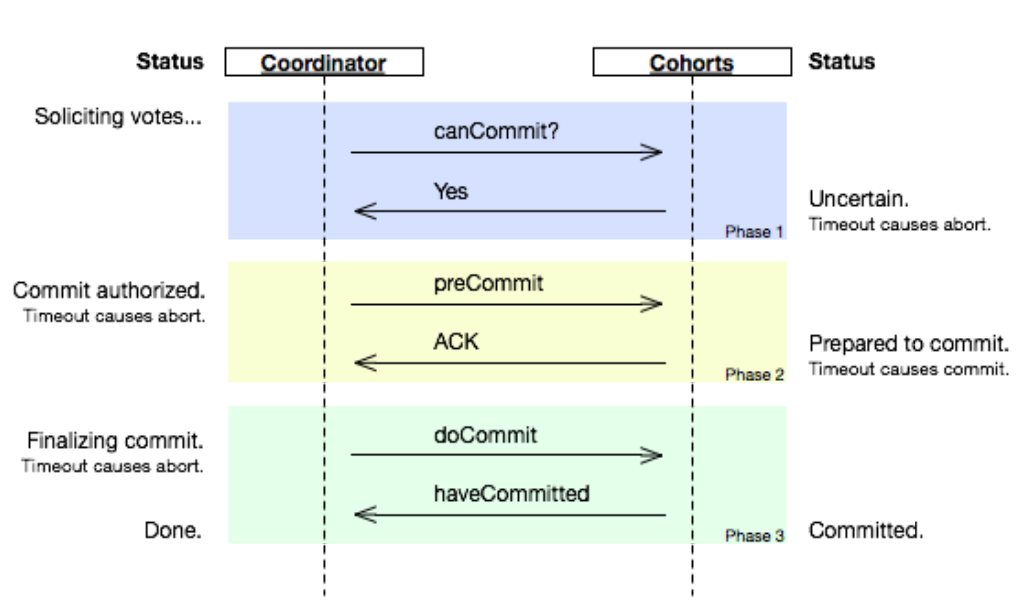
强一致性的皇冠:分布式事务模型的至高法则揭秘
关注微信公众号 “程序员小胖” 每日技术干货,第一时间送达! 引言 分布式事务模型是分布式系统设计的核心,关键在于保证数据一致性和事务完整性,尤其强调强一致性。诸如2PC、3PC、Saga、TCC等模型与协议,应运而生以解…...
mac/windows下安装docker,minikube
1、安装docker Get Started | Docker 下载安装docker 就行 启动后,就可以正常操作docker了 使用docker -v 验证是否成功就行 2、安装minikube,是基于docker-desktop的 2.1、点击设置 2.2、选中安装,这个可能需要一点时间 这样安装后&…...
和find_all()))
【爬虫】fake_useragent的使用、BeautifulSoup(find()和find_all())
1 fake_useragent 2 BeautifulSoup 3 Beautiful Soup库的find()和find_all() 1 fake_useragent fake_useragent是一个Python库,用于生成随机的用户代理字符串。 用户代理是在HTTP请求中发送给服务器的一种标识,它告诉服务器发送请求的客户端的类型、版本…...
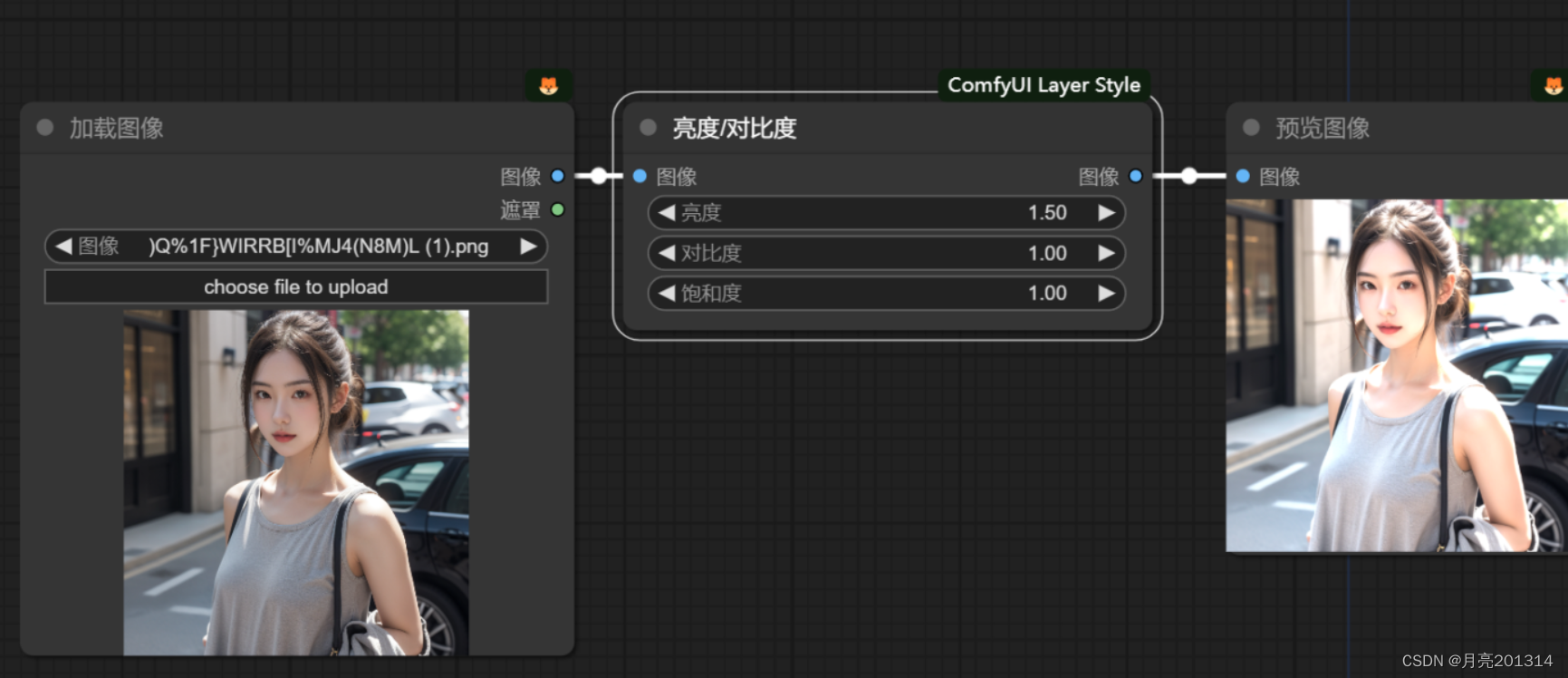
ComfyUI中图像亮度/对比度/饱和度处理
用上面这个节点可以同时设置图片的亮度、对比度和饱和度。 【保姆级教程】一口气分享在ComfyUI中常用的30多种基本图像处理方式 更多好玩且实用AIGC工作流和节点 星球号:32767063 本期资料链接 往期学习资料 整理AI学习资料库...

基于FPGA的DDS波形发生器VHDL代码Quartus仿真
名称:基于FPGA的DDS波形发生器VHDL代码Quartus仿真(文末获取) 软件:Quartus 语言:VHDL 代码功能: DDS波形发生器VHDL 1、可以输出正弦波、方波、三角波 2、可以控制输出波形的频率 DDS波形发生器原理…...

C++语法|可调用对象与function类型
文章目录 引入function的使用function类型的典型应用function类型的原理实现代码优化可变参的函数对象 引入 还记得C语言中的函数指针数组吗? 我们通过函数指针数组实现一个,图书管理系统的界面: #include <stdio.h> void doShowAllB…...

Linux学习之路 -- 文件 -- 文件描述符
前面介绍了与文件相关的各种操作,其中的各个接口都离不开一个整数,那就是文件描述符,本文将介绍文件描述符的一些相关知识。 目录 <1>现象 <2>原理 文件fd的分配规则和利用规则实现重定向 <1>现象 我们可以先通过prin…...

JDK动态代理和Cglib动态代理区别
1.如果目标类实现了接口,将会使用JDK动态代理,否则会使用Cglib动态代理; 2.JDK代理使用自己的字节码生成工具生成代理对象,而Cglib会使用ASM字节码生成工具去生成; 3.JDK动态代理是通过反射的方式去实现代理对象的所有方法,通过…...
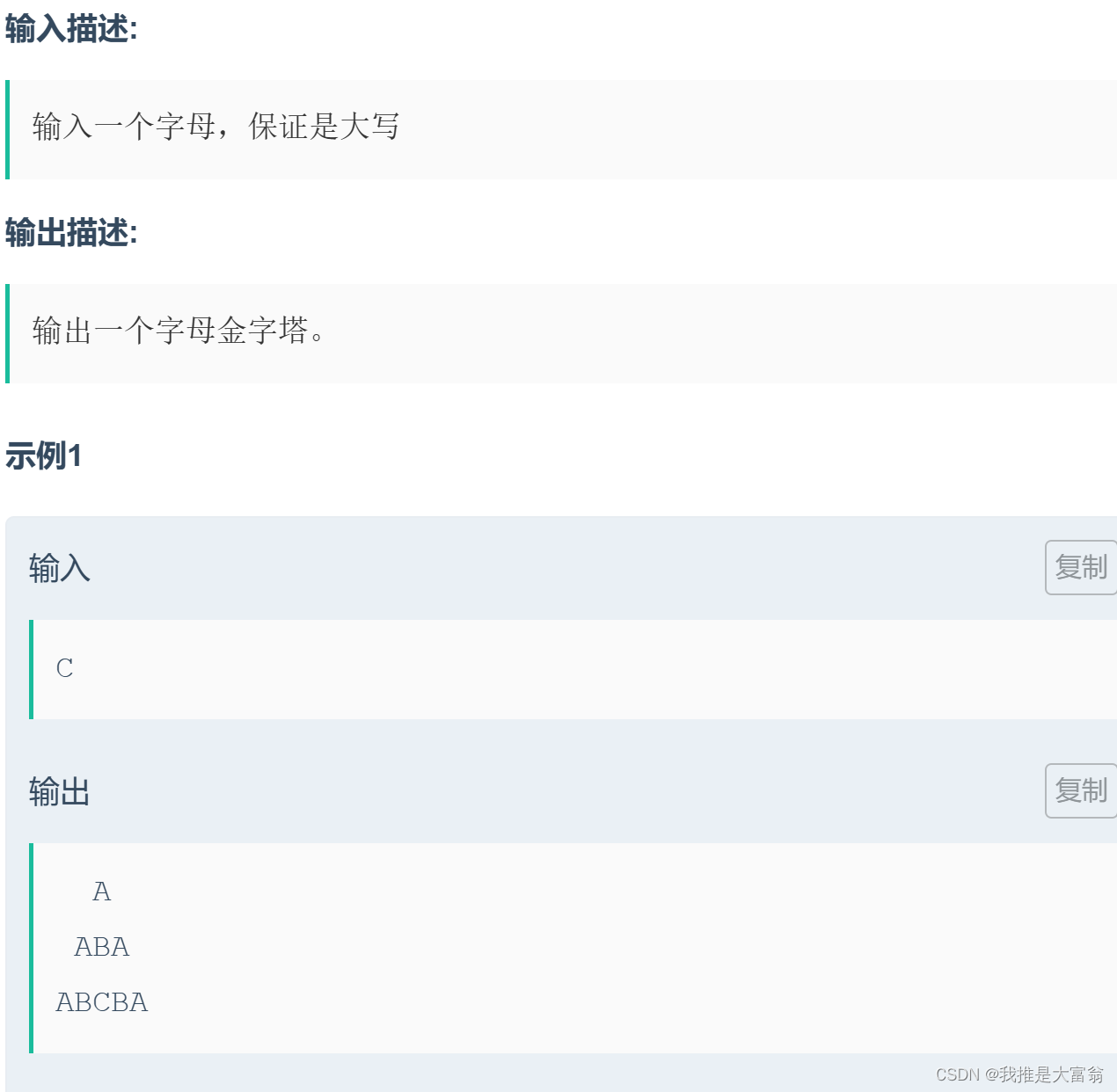
牛客 | 字符金字塔
请打印输出一个字符金字塔,字符金字塔的特征请参考样例 #include <stdio.h> #include <string.h> using namespace std; int main() {char c;scanf("%c", &c);for (int i 1; i < (c - 64); i)//第一个循环决定了有多少行{//c:67 第三…...

【计算机科学速成课】笔记三——操作系统
文章目录 18.操作系统问题引出——批处理设备驱动程序多任务处理虚拟内存内存保护Unix 18.操作系统 问题引出—— Computers in the 1940s and early 50s ran one program at a time. 1940,1950 年代的电脑,每次只能运行一个程序 A programmer would write one at…...

用js代码实现贪吃蛇小游戏
js已经学了大部分了,现在就利用我所学的js知识试试做贪吃蛇小游戏吧 以下部分相关图片以及思路笔记均出自渡一陈老师的视频 首先制作简单的静态页面,添加贪吃蛇移动的背景和相关图片,比如开始游戏等等 将各个功能均封装在函数中࿰…...

微信小程序+esp8266温湿度读取
本文主要使用微信小程序显示ESP8266读取的温湿度并通过微信小程序控制LED灯。小程序界面如下图所示 原理讲解 esp8266 通过mqtt发布消息,微信小程序通过mqtt 订阅消息,小程序订阅后,就可以实时收到esp8266 传输来的消息。 个人可免费注册五个微信小程序账号,在微信小程序官…...

软考中级-软件设计师(十)网络与信息安全基础知识
一、网络概述 1.1计算机网络的概念 计算机网络的发展:具有通信功能的单机系统->具有通信功能的多机系统->以共享资源为目的的计算机网络->以局域网及因特网为支撑环境的分布式计算机系统 计算机网络的功能:数据通信、资源共享、负载均衡、高…...

推荐一个好用的命令行工具ShellGPT
ShellGPT 配置安装常用功能聊天写命令并执行 高级功能函数调用角色管理 总结 这两天突然想到,现有的很多工具都在被大模型重构,比如诞生了像perplexity.ai 这种新交互形式的搜索引擎,就连wps也推出了AI服务,甚至都可以直接生成ppt…...
Prompt提示词教程 | 提示工程指南 | 提示词示例 入门篇
在上一节中,我们介绍并给出了如何赋能大语言模型的基本示例。如果还没看而且是刚入门的同学建议看下,有个基本概念。 Prompt提示词教程 | 提示工程指南 | 提示工程简介https://blog.csdn.net/HRG520JN/article/details/138523705在本节中,我…...
uniapp + uView动态表单校验
项目需求:动态循环表单,并实现动态表单校验 页面: <u--form label-position"top" :model"tmForm" ref"tmForm" label-width"0px" :rulesrules><div v-for"(element, index) in tmForm…...

【Linux】HTTPS
欢迎来到Cefler的博客😁 🕌博客主页:折纸花满衣 🏠个人专栏:Linux 目录 👉🏻HTTPS协议概念👉🏻加密为什么要进行加密 👉🏻常见的加密方式对称加密…...
语音识别--使用YAMNet识别环境音
⚠申明: 未经许可,禁止以任何形式转载,若要引用,请标注链接地址。 全文共计3077字,阅读大概需要3分钟 🌈更多学习内容, 欢迎👏关注👀【文末】我的个人微信公众号…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

echarts使用graphic强行给图增加一个边框(边框根据自己的图形大小设置)- 适用于无法使用dom的样式
pdf-lib https://blog.csdn.net/Shi_haoliu/article/details/148157624?spm1001.2014.3001.5501 为了完成在pdf中导出echarts图,如果边框加在dom上面,pdf-lib导出svg的时候并不会导出边框,所以只能在echarts图上面加边框 grid的边框是在图里…...
