C语言----汉诺塔问题
1.什么是汉诺塔问题
简单来说,就是有三个柱子,分别为A柱,B柱,C柱。其中A柱从上往下存放着从小到大的圆盘,我们需要借助B柱和C柱,将A柱上的所有圆盘转移到C柱上,并且一次只能移动一个圆盘,且在移动的过程中,大圆盘不能再小圆盘的上面。
2.思路分析
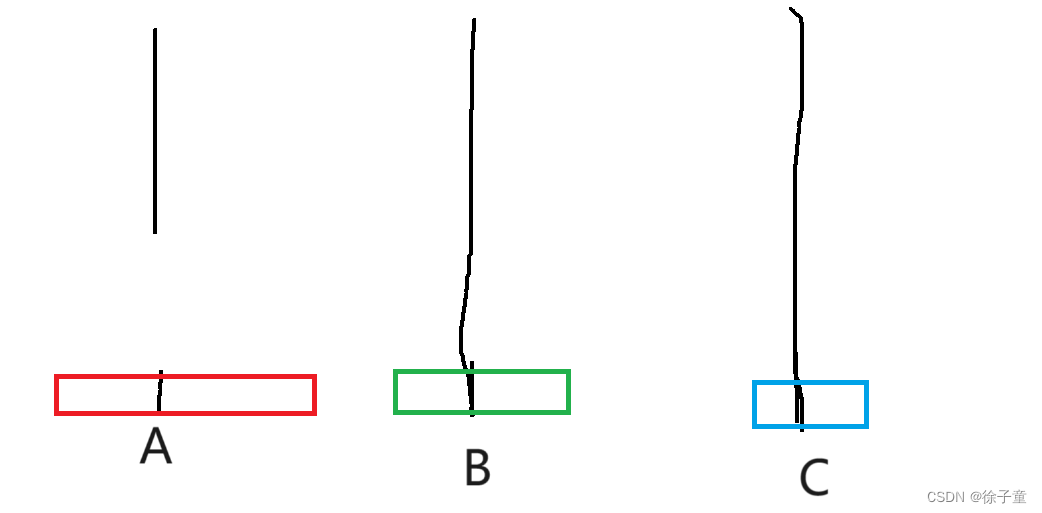
首先,我们的最终目的是将A柱上的圆盘全部转移到C柱上。则当A柱上只有一个圆盘,我们直接将A柱上的圆盘转移到C柱上就行了。
如下图所示
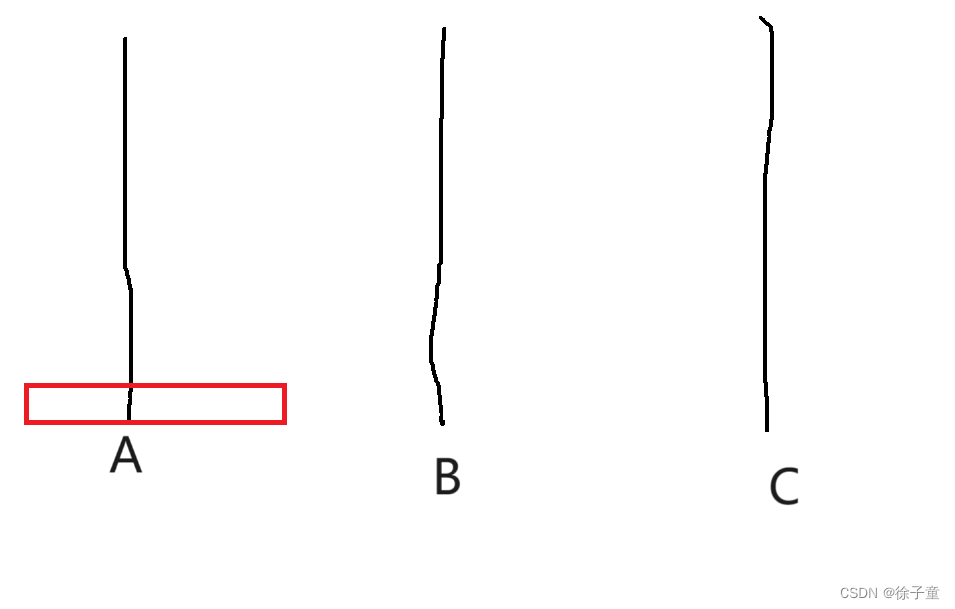
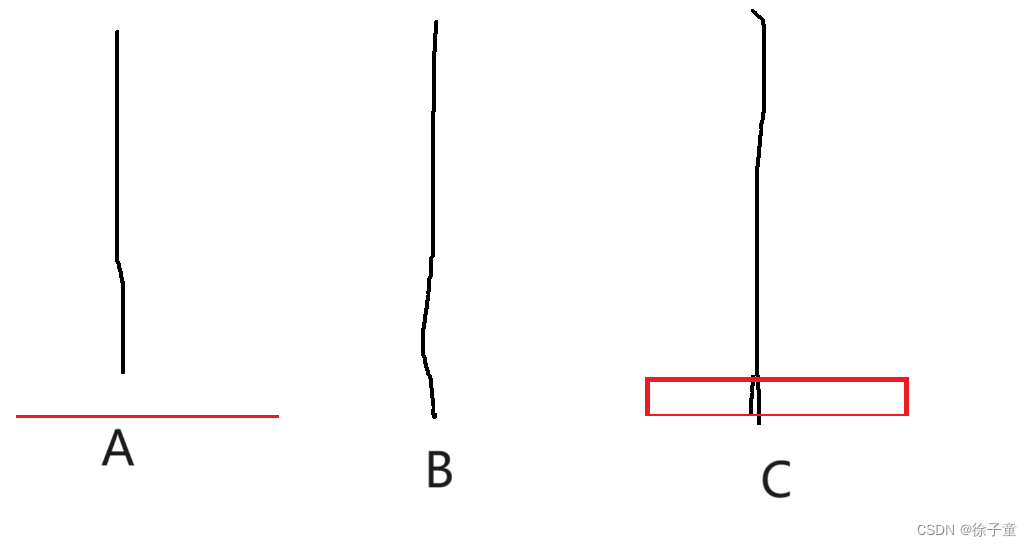
当A柱上有多个圆盘时,就很复杂了,我们需要慢慢来分析。
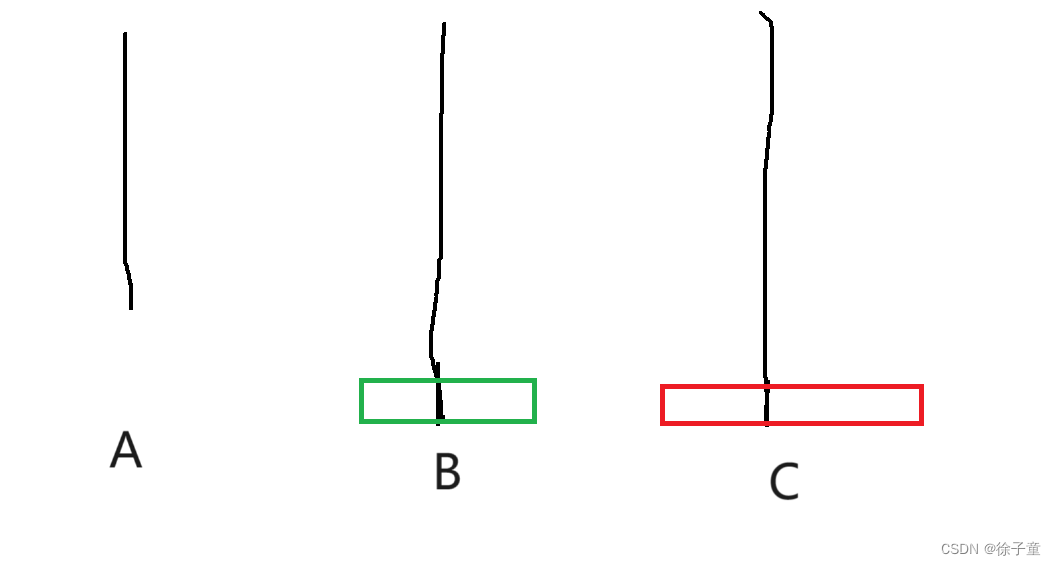
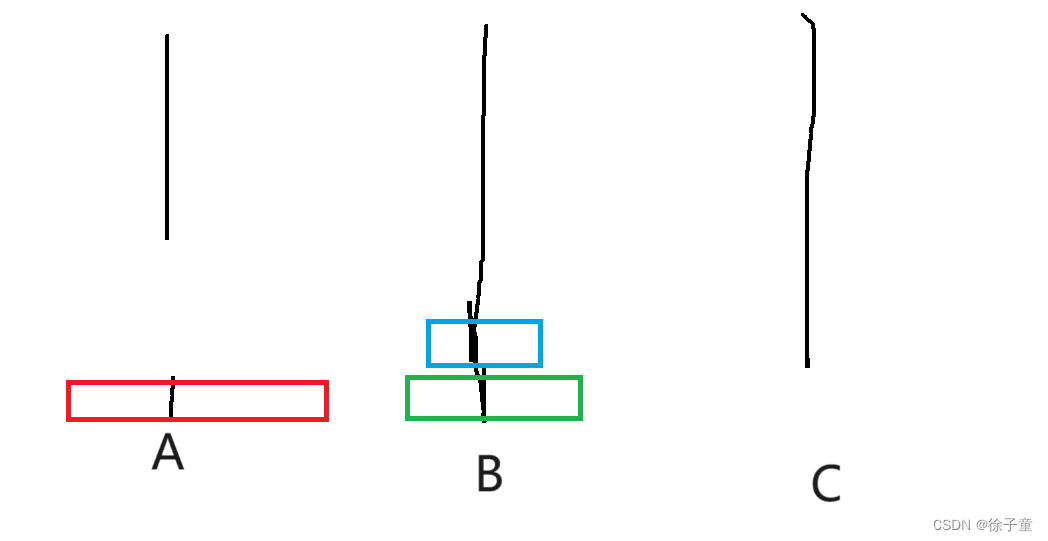
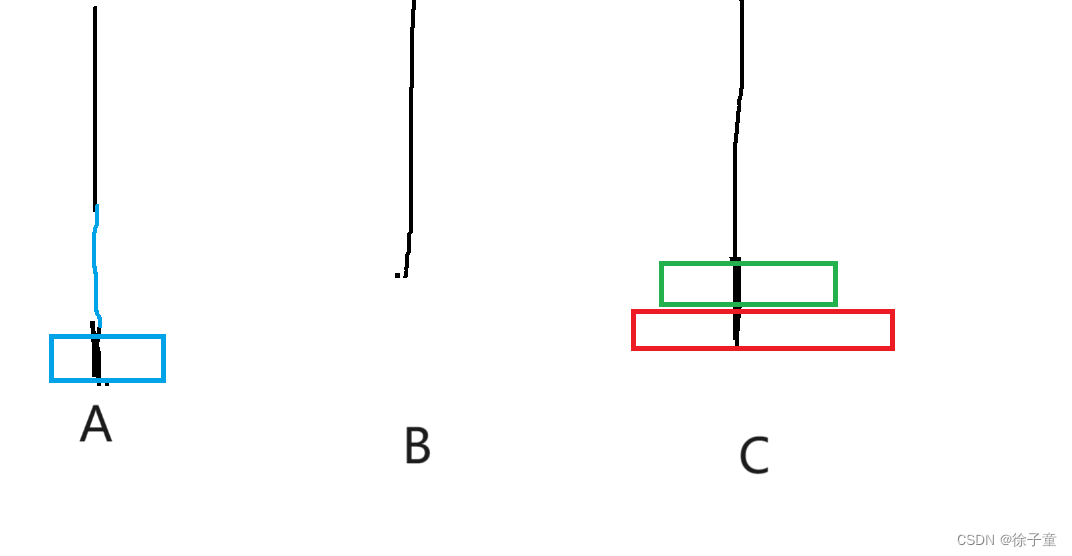
当A柱上有2个圆盘时。我们要先将第一个圆盘转移到B柱上,然后再将第二个圆盘转移到C柱上,然后再将B柱上的圆盘转移到C柱上。
简化为 A->B A->C B->C。
如下图所示
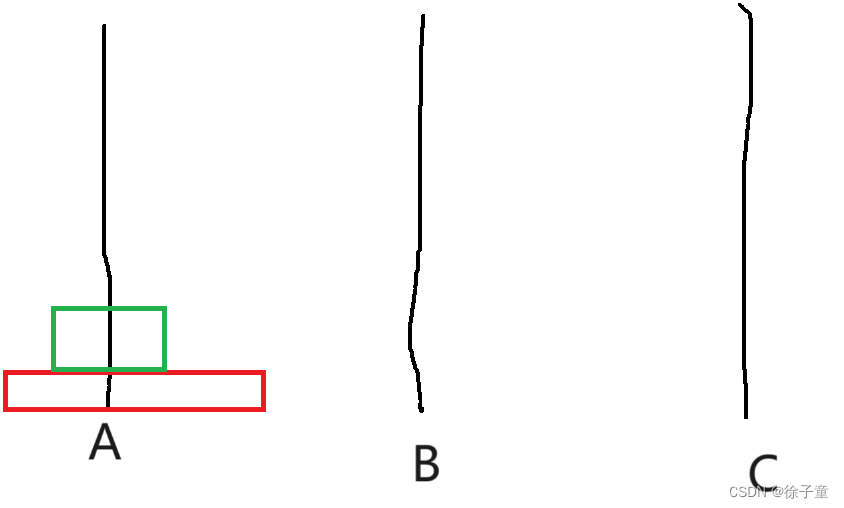
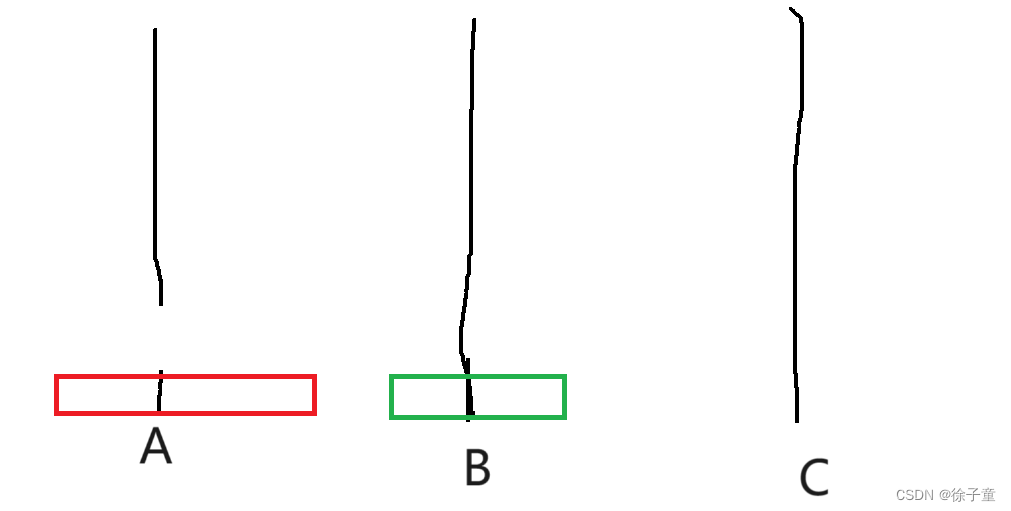
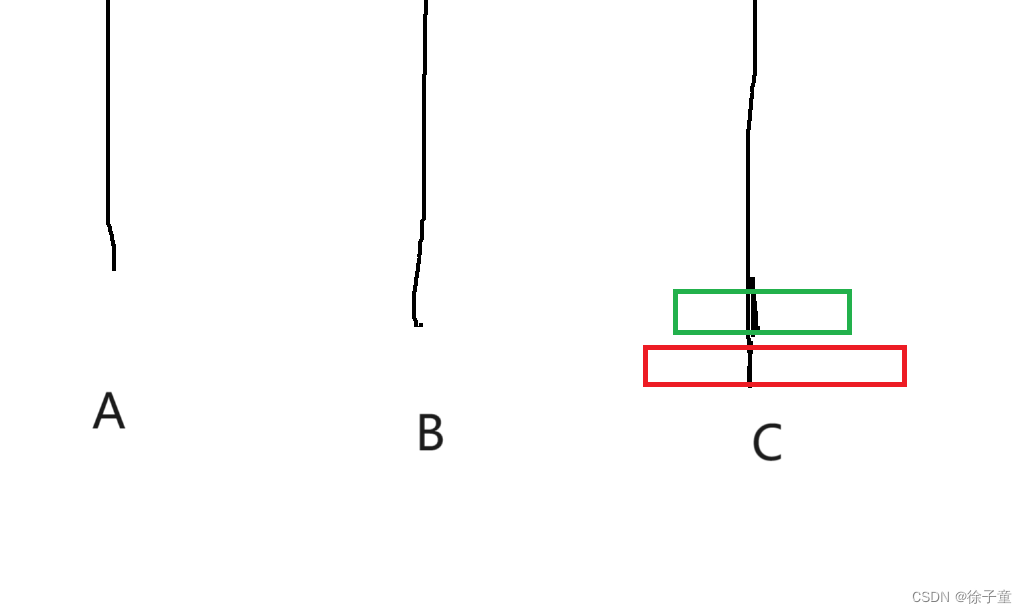
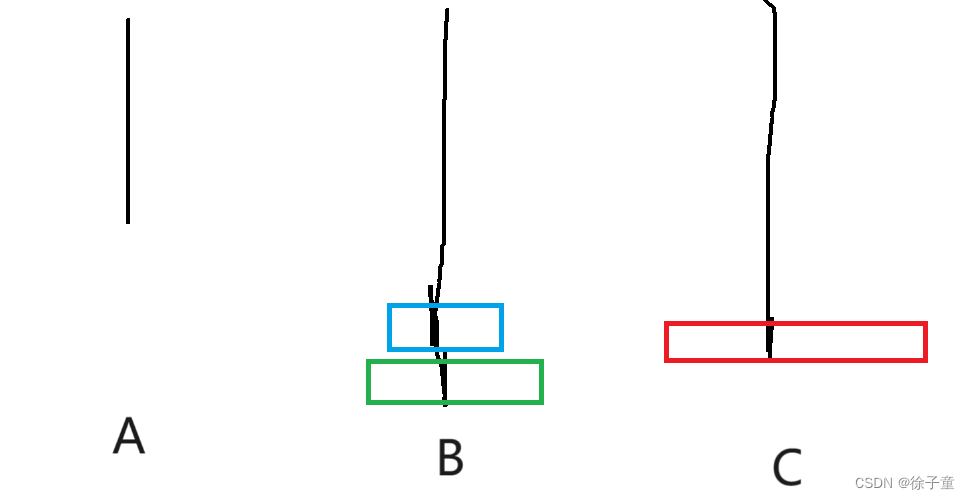
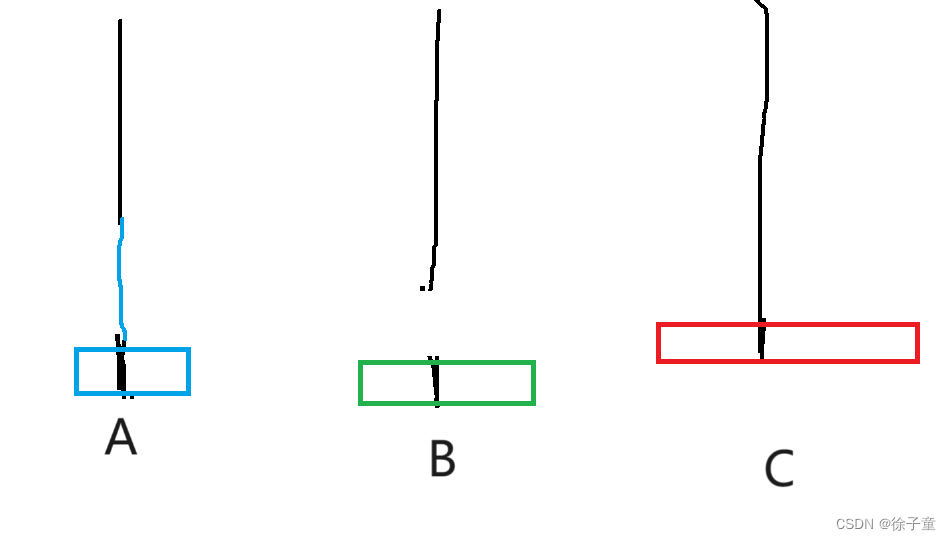
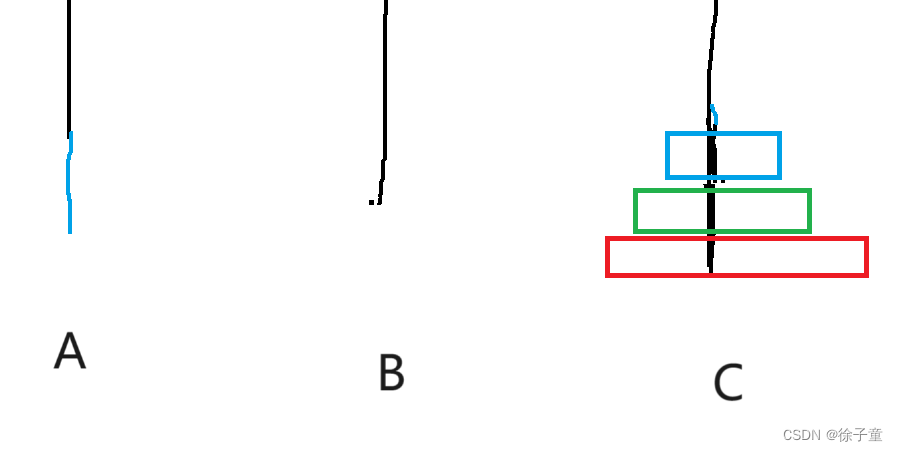
当有3个圆盘时。
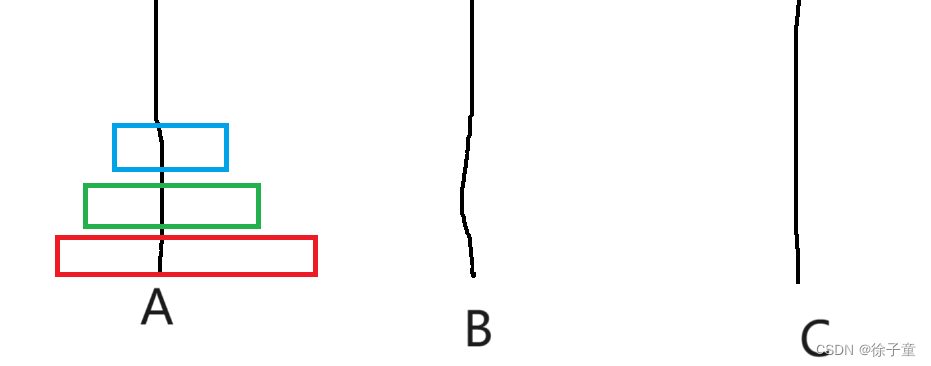
我们先将A盘上的第一个盘子转移到C柱,再将A柱上的第二个圆盘转移到B柱上,接着再将C盘上的圆盘转移到B柱上,再将A柱上的最后一个圆盘转移到C柱上,接着再将B柱上的第一个圆盘转移到A柱上,再将B柱上的最后一个圆盘转移到C柱上,接着再将A柱上的圆盘转移到C柱上,就完成了。
简化来说,A->C A->B C->B A->C B->A B->C A->C。
如下图所示
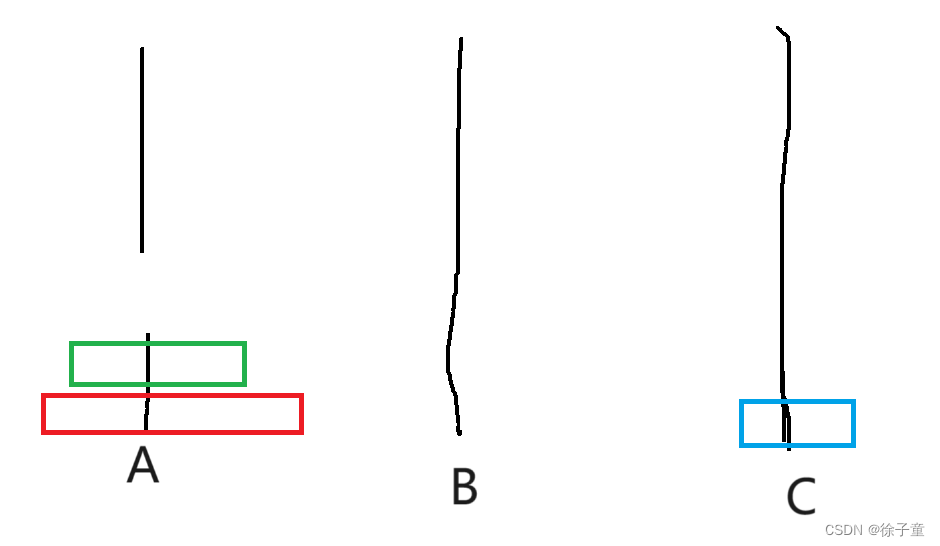
通过2个圆盘和3个圆盘的例子发现,要向将A柱上的圆盘按要求转移到C柱上,我们要将n-1个圆盘全部转移到B柱上。
代码实现
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
int count = 0;//全局变量做计数器
void move(char Tower_1, char Tower_2)
{printf("将 %c 移动到 %c \n", Tower_1, Tower_2);count++;
}
void Hanoi(int n, char Tower_1, char Tower_2, char Tower_3)
{if (n == 1)//是一个的话就直接从Tower_1移动到Tower_3move(Tower_1, Tower_3);else{//不是一个的话先借助Tower_3将Tower_1上面的n-1个移动到Tower_2Hanoi(n - 1, Tower_1, Tower_3, Tower_2);//完成此过程后Tower_1上面还有最后一个 move(Tower_1, Tower_3); //将Tower_1上面的最后一个移动到Tower_3//将Tower_2上面的n-1个通过Tower_1移动到Tower_3Hanoi(n - 1, Tower_2, Tower_1, Tower_3);}
}
int main()
{printf("请输入圆盘个数:\n");int n = 0;scanf("%d", &n);Hanoi(n, 'A', 'B', 'C');printf("一共进行了%d次", count);return 0;
}汉诺塔问题涉及到了递归的的问题,其里面有两个递归的过程,其实十分复杂的。
相关文章:

C语言----汉诺塔问题
1.什么是汉诺塔问题 简单来说,就是有三个柱子,分别为A柱,B柱,C柱。其中A柱从上往下存放着从小到大的圆盘,我们需要借助B柱和C柱,将A柱上的所有圆盘转移到C柱上,并且一次只能移动一个圆盘&#…...

Python中驼峰命名法和下划线命名法相互转换的实战代码
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...
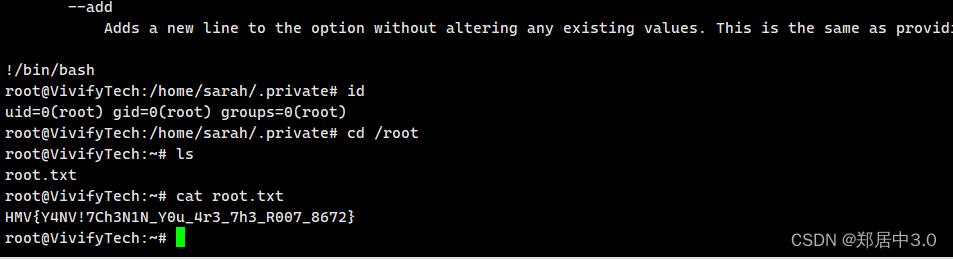
【hackmyvm】vivifytech靶机
渗透思路 信息收集端口扫描端口服务信息目录扫描爆破hydra--sshgit提权 信息收集 ┌──(kali㉿kali)-[~] └─$ fping -ag 192.168.9.0/24 2>/dev/null 192.168.9.119 --主机 192.168.9.164 --靶机个人习惯,也方便后续操作,将IP地址赋值给一个变…...

纯血鸿蒙APP实战开发——手写绘制及保存图片
介绍 本示例使用drawing库的Pen和Path结合NodeContainer组件实现手写绘制功能。手写板上完成绘制后,通过调用image库的packToFile和packing接口将手写板的绘制内容保存为图片,并将图片文件保存在应用沙箱路径中。 效果图预览 使用说明 在虚线区域手写…...

在什么情况下表单会被重复提交?如何避免?
表单被重复提交是Web应用中常见的问题,通常在用户提交表单后点击按钮多次,或在表单提交后刷新页面时发生。这可能导致数据的重复处理,比如重复记录或订单。 何时会发生表单重复提交? 用户多次点击提交按钮:在网络延迟…...

JavaScript 中的 Class 类
🔥 个人主页:空白诗 文章目录 🔥 引言🎯 基础知识🏗️ 构造函数 (Constructor)🔐 私有字段 (Private Fields)🔐 私有方法 (Private Methods)🧬 继承 (Inheritance)📦 静态…...
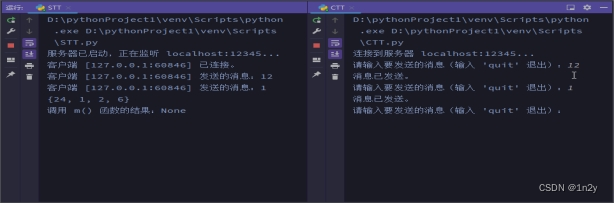
python实验三 实现UDP协议、TCP协议进行服务器端与客户端的交互
实验三 实验题目 1、请利用生成器构造一下求阶乘的函数Factorial(),定义一个函数m(),在m()中调用生成器Factorial()生成小于100的阶乘序列存入集合s中,输出s。 【代码】 def factorial():n1f1while 1: f * n yield (f) n1…...
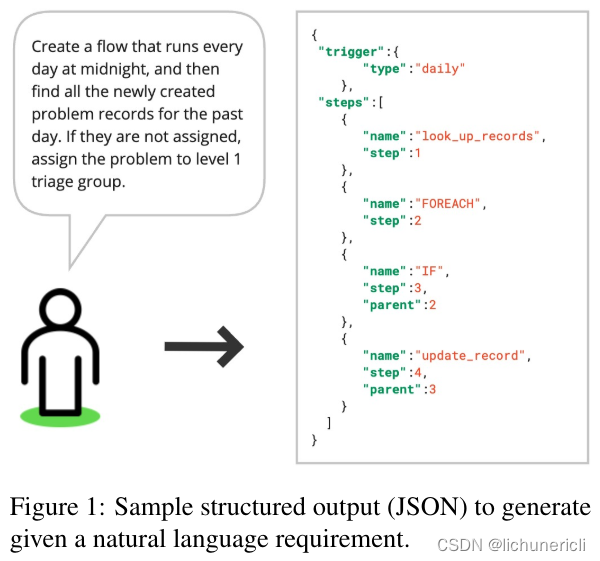
ServiceNow 研究:通过RAG减少结构化输出中的幻觉
论文地址:https://arxiv.org/pdf/2404.08189 原文地址:rag-hallucination-structure-research-by-servicenow 在灾难性遗忘和模型漂移中,幻觉仍然是一个挑战。 2024 年 4 月 18 日 灾难性遗忘: 这是在序列学习或连续学习环境中出现…...
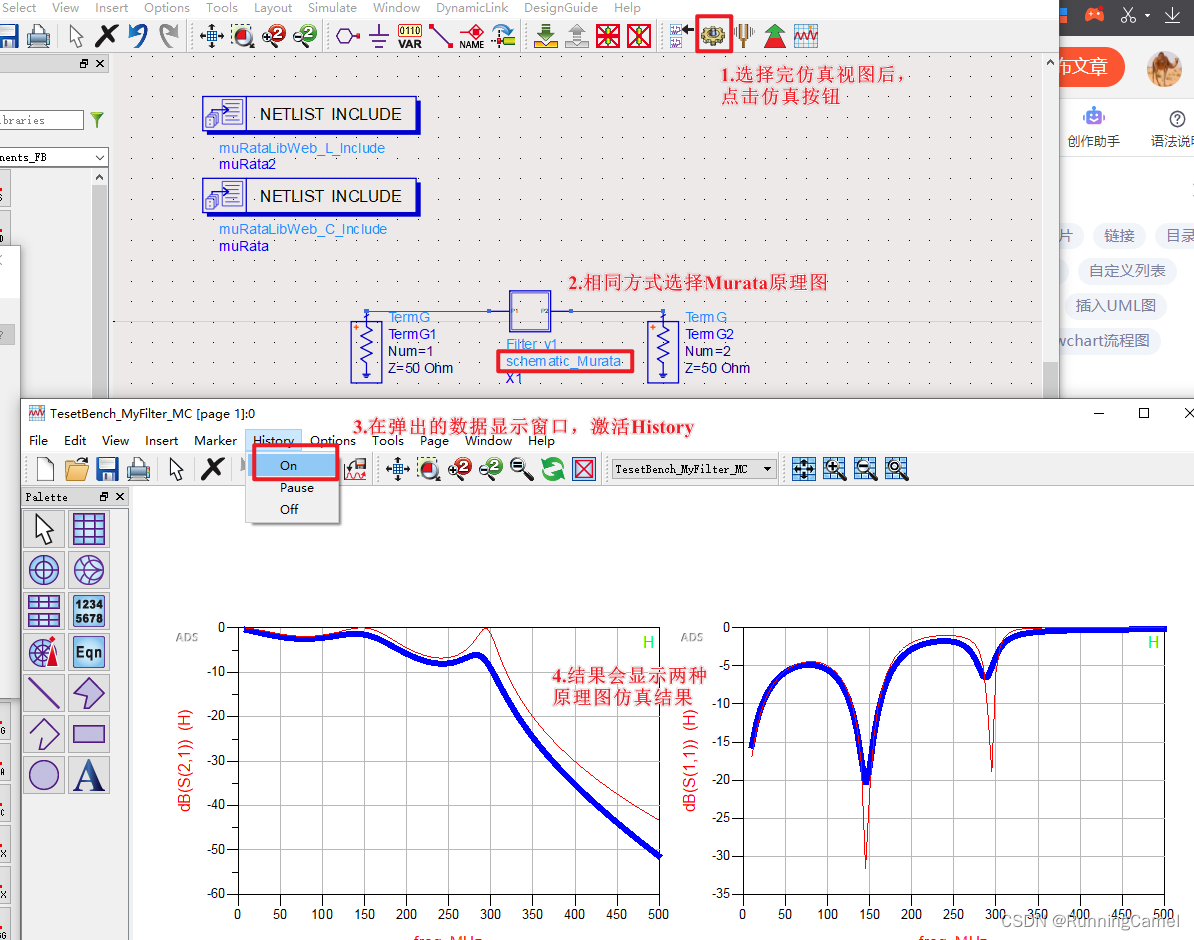
ADS基础教程10-多态性(动态模型选择)
目录 一、多态性定义二、操作步骤1.模型建立2.模型选择3.执行仿真 一、多态性定义 ADS中支持一个Symbol中,可以同时存在多个子图。在仿真时可以动态选择不同的子图继续宁仿真。 二、操作步骤 1.模型建立 在上一章A…...
代码随想录第四十六天|单词拆分
题目链接:. - 力扣(LeetCode)...

RabbitMQ的介绍和使用
1.同步通讯和异步通讯 举个例子,同步通讯就像是在打电话,因此它时效性较强,可以立即得到结果,但如果你正在和一个MM打电话,其他MM找你的话,你们之间是不能进行消息的传递和响应的 异步通讯就像是微信&#…...

前端get请求日期类型参数向后端传参失败
1、背景 get请求,通过url上传参,因此日期类型是string类型数据 2、异常信息 nested exception is org.springframework.core.convert.ConversionFailedException: Failed to convert from type [java.lang.String] to type [java.time.LocalDate] for…...

【docker 】 push 镜像提示:denied: requested access to the resource is denied
往 Docker Registry (私服)push 镜像提示:denied: requested access to the resource is denied 镜像push 语法:docker push <registry-host>:<registry-port>/<repository>:<tag> docker push 192.16…...
总结)
浏览器各类好用插件使用及常见问题(技巧)总结
目录 Vimium C快捷键问题为什么Vimium C - 全键盘操作浏览器插件在百度页面中, x ,o,f等快捷键不起作用如何使用viminum c插件进行自定义快捷键?vimucm 为什么在浏览器首页时快捷键不起作用? 网页截图问题firefox 网页截图使用 idm问题浏览器点击idm 不下载? 待续、更新中 V…...
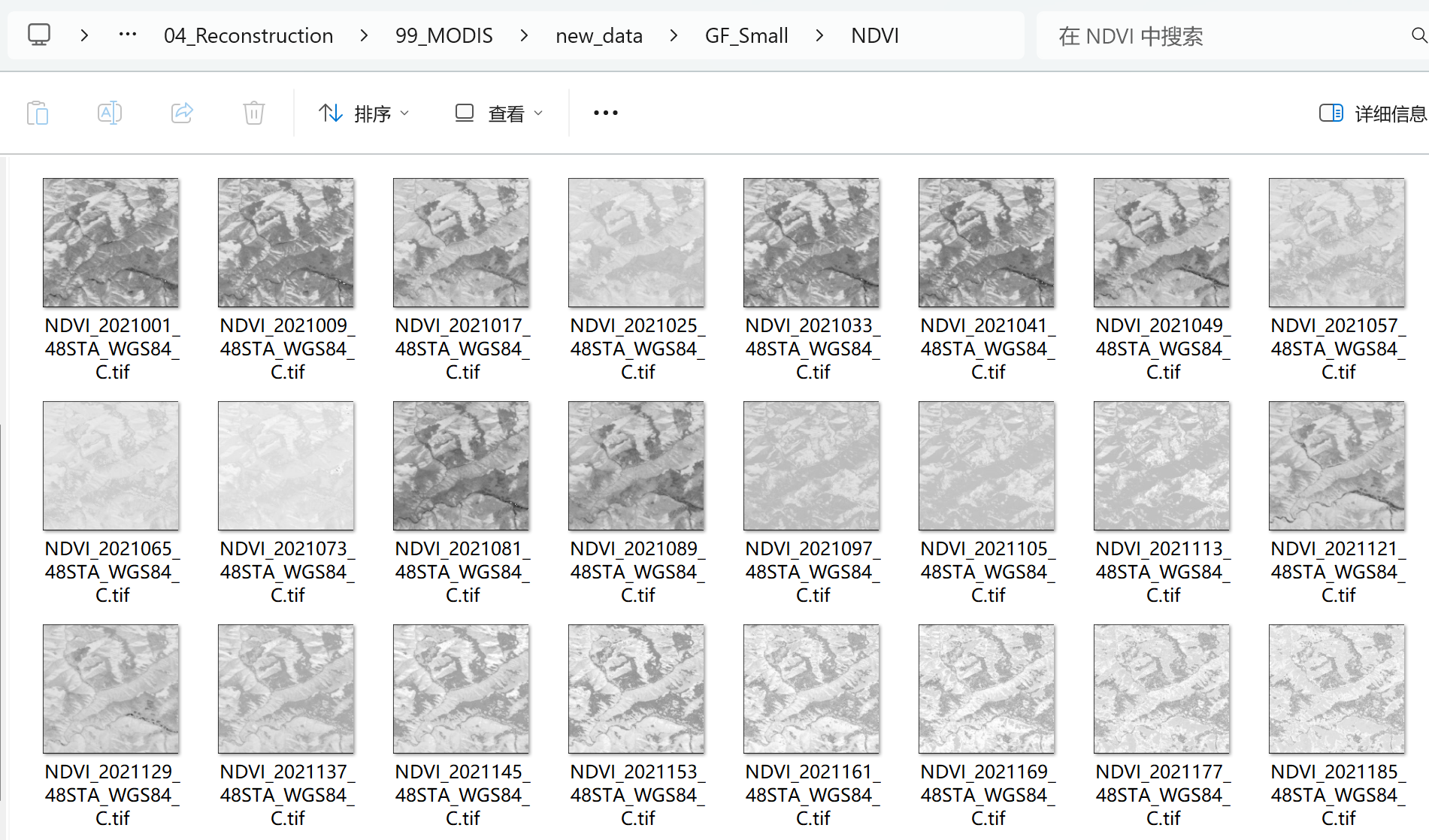
Python批量计算多张遥感影像的NDVI
本文介绍基于Python中的gdal模块,批量基于大量多波段遥感影像文件,计算其每1景图像各自的NDVI数值,并将多景结果依次保存为栅格文件的方法。 如下图所示,现在有大量.tif格式的遥感影像文件,其中均含有红光波段与近红外…...

6.k8s中的secrets资源
一、Secret secrets资源,类似于configmap资源,只是secrets资源是用来传递重要的信息的; secret资源就是将value的值使用base64编译后传输,当pod引用secret后,k8s会自动将其base64的编码,反编译回正常的字符…...

git 更换远程仓库地址三种方法总结
git 更换远程仓库地址三种方法总结 一、前言 由于私服的 gitlab 的地址变更,导致部分项目代码提交不上去,需要修改远端仓地址。 其它需要修改远程仓地址的情况如:切换git clone 协议由ssh变为https。 二、环境 windows 10git version 2.3…...
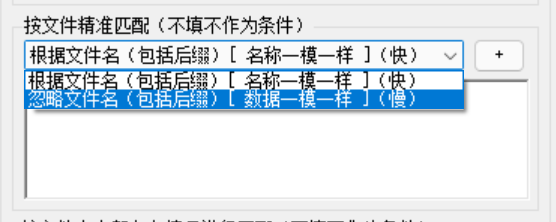
快速找出存(不存在)在某个(或多个)文件的文件夹
首先,需要用到的这个工具: 度娘网盘 提取码:qwu2 蓝奏云 提取码:2r1z 想要找出有下面这个文件存在的文件夹 切换到批量文件复制版块,快捷键Ctrl5 右侧,搜索添加 选定范围,勾选搜索文件夹、包…...
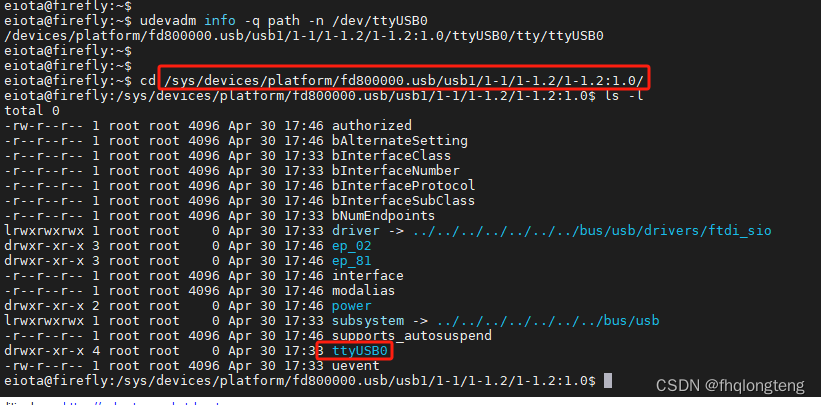
Linux USB转串口设备路径的查找方法
1、USB转串口设备 USB转串口设备是在嵌入式软件开发过程中经常要使用的,常常用于对接各种各样的串口设备。如果一台linux主机上使用多个usb转串口设备时,应用程序中就需要知道自己操作的是哪个串口设备。串口设备在系统上电时,由于驱动加载的…...

【初阶数据结构】单链表之环形链表
目录标题 前言环形链表的约瑟夫问题环形链表环形链表|| 前言 前面我们已经学习了关于单链表的一些基本东西,今天我们来学习单链表的一个拓展——环形链表,我们将用力扣和牛客网上的三道题目来分析讲解环形链表问题。 环形链表的约瑟夫问题 我们首先来看…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

Qt的学习(一)
1.什么是Qt Qt特指用来进行桌面应用开发(电脑上写的程序)涉及到的一套技术Qt无法开发网页前端,也不能开发移动应用。 客户端开发的重要任务:编写和用户交互的界面。一般来说和用户交互的界面,有两种典型风格&…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...
