费马小定理详解
费马小定理
定义:
设 p 为素数,a 为整数,则 a p ≡ a ( m o d p ) a^p \equiv a\ (\mod p) ap≡a (modp) ,若 p ∤ a p \nmid a p∤a ,则 a p − 1 ≡ 1 ( m o d p ) a^{p-1} \equiv 1\ (\mod p) ap−1≡1 (modp)
先证明若 p ∣ a p \mid a p∣a ,证明过程如下:
∵ p ∣ a a m o d p = 0 a p m o d p = 0 \because p \mid a \\ a\mod p=0 \\ a^p \mod p =0 ∵p∣aamodp=0apmodp=0
再证明当 p ∤ a p \nmid a p∤a 时:
创建集合 S = S= S={ x 1 , x 2 , x 3 , ⋯ , x p − 1 x_1,x_2,x_3,\cdots,x_{p-1} x1,x2,x3,⋯,xp−1} ,S为1,2,3, ⋯ \cdots ⋯,p-1的一个 排列 , a x 1 , a x 2 , a x 3 , ⋯ , a x p − 1 ax_1,ax_2,ax_3,\cdots,ax_{p-1} ax1,ax2,ax3,⋯,axp−1 ,任意两项模 p 不同余
若 ∃ ∀ i , j , ╞ 1 ≤ i < j < p \exists\ \forall\ i,j,╞ 1\le i <j <p ∃ ∀ i,j,╞1≤i<j<p ,使得 a x i ≡ a x j ( m o d p ) ax_i\ \equiv ax_j (\mod p) axi ≡axj(modp)
则 p ∣ a ( x i − x j ) p\mid a(x_i-x_j) p∣a(xi−xj)
∵ p ∤ a , ∴ p ∣ ( x i − x j ) \because p \nmid a\ \ ,\therefore p\mid(x_i-x_j) ∵p∤a ,∴p∣(xi−xj)
又 ∵ x i m o d p ≠ x j m o d p \because x_i \mod p \not= x_j\mod p ∵ximodp=xjmodp
∴ 矛盾 \therefore 矛盾 ∴矛盾
设 ∀ k ∈ S , p ∤ S k \forall \ k \in S,p\ \nmid\ S_k ∀ k∈S,p ∤ Sk
∵ a x 1 m o d p , a x 2 m o d p , ⋯ , a x p − 1 m o d p \because ax_1\mod p,ax_2\mod p,\cdots,ax_{p-1}\mod p ∵ax1modp,ax2modp,⋯,axp−1modp 为1,2,3, ⋯ \cdots ⋯ ,p-1的一个排列(上文已提到)
∴ ( a x 1 ) ( a x 2 ) ( a x 3 ) ⋯ ( a x p − 1 ) ≡ x 1 ⋅ x 2 ⋅ x 3 ⋯ x p − 1 ( m o d p ) \therefore (ax_1)(ax_2)(ax_3)\cdots(ax_{p-1})\equiv x_1\cdot x_2\cdot x_3 \cdots x_{p-1} (\mod p) ∴(ax1)(ax2)(ax3)⋯(axp−1)≡x1⋅x2⋅x3⋯xp−1(modp)
x 1 ⋅ x 2 ⋅ x 3 ⋯ x p − 1 = ( p − 1 ) ( p − 2 ) ( p − 3 ) ⋯ 2 ⋅ 1 = ( p − 1 ) ! x_1\cdot x_2 \cdot x_3 \cdots x_{p-1} \\ =(p-1)(p-2)(p-3)\cdots 2\cdot 1 \\ =(p-1)! x1⋅x2⋅x3⋯xp−1=(p−1)(p−2)(p−3)⋯2⋅1=(p−1)!
∵ p ∤ ( p − 1 ) ! \because p\nmid(p-1)! ∵p∤(p−1)!
∴ a p − 1 ≡ 1 ( m o d p ) \therefore a^{p-1}\equiv 1 (\mod p) ∴ap−1≡1(modp)
得证
相关文章:

费马小定理详解
费马小定理 定义: 设 p 为素数,a 为整数,则 a p ≡ a ( m o d p ) a^p \equiv a\ (\mod p) ap≡a (modp) ,若 p ∤ a p \nmid a p∤a ,则 a p − 1 ≡ 1 ( m o d p ) a^{p-1} \equiv 1\ (\mod p) ap−1≡1 (modp)…...

PXE批量安装
系统装机的三种引导方式 u盘光盘网络装机 光盘: 1.类似于usb模式 2.刻录模式 系统安装过程 加载boot loader Boot Loader 是在操作系统内核运行之前运行的一段小程序。通过这段小程序,我们可以初始化硬件设备、建立内存空间的映射图,从…...

stm32f103c8t6最小系统板
STM32F103C8T6最小系统板是为基于ARM Cortex-M3内核的STM32F103C8T6微控制器设计的电路板,它包含了单片机正常运行所需的最基本组件。以下是构成STM32F103C8T6最小系统板的基本部分: 单片机芯片:STM32F103C8T6本身,它是一款32位微…...
)
QCefView 在 Linux 下的编译(更新)
在前面的文章《QT 应用程序中集成浏览器》中已经介绍过 QCefView 的构建。这几天发现 QCefView 代码进行了更新,构建方式也发生了一点点变化,所以在此更新一下 QCefView 的编译方法。 QCefView 其实包含了两个项目,一个就是 QCefView 项目本身,另外一个就是 CefViewCore。…...

无卤素产品是什么?有什么作用?
无卤素产品,即在生产过程中完全不使用卤素元素——氟、氯、溴、碘等——的产品。 卤素元素,虽然在电子设备、材料等领域应用广泛,却也可能潜藏危害。其阻燃剂,一旦在产品生命周期结束后释放,将对土壤和水体造成污染&a…...
esp32-cam 1. 出厂固件编译与测试
0. 环境 - ubuntu18 - esp32-cam - usb转ttl ch340 硬件连接 esp32-camch340板子U0RTXDU0TRXDGNDGND5V5V 1. 安装依赖 sudo apt-get install vim sudo apt install git sudo apt-get install git wget flex bison gperf python python-pip python-setuptools python-serial p…...

题目:线性代数
问题描述: 解题思路: 列相乘,然后行相加。 注意点:由于元素数据范围最大为1e6,两个元素相乘乘积最大为1e12,如果元素类型为int则在乘的过程中就会爆炸,所以需要开long long类型。 AC代码…...
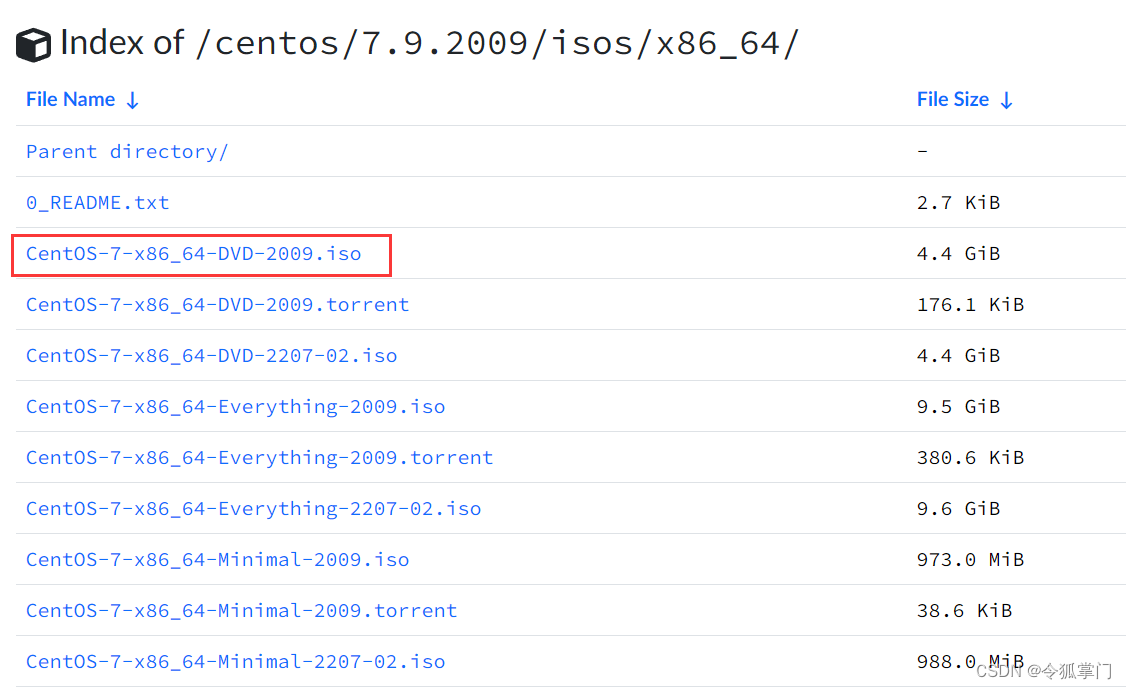
docker学习笔记3:VmWare CentOS7安装与静态ip配置
文章目录 一、安装CentOS71、下载centos镜像2、安装二、设置静态ip三、xshell连接centos本专栏的docker环境是在centos7里安装,因此首先需要会安装centos虚拟机。 本篇博客介绍如何在vm虚拟机里安装centos7。 一、安装CentOS7 1、下载centos镜像 推荐清华源,下载如下版本 …...

leetcode 547.省份数量
思路:dfs 或者这道题用bfs也是可以的。 这道题有点迷惑性,这里的数组给的是无向图的数组,而并不是地图,这里需要着重注意一下。 而后,这里的状态数组st没必要是二维的,我们并不会去遍历所给的数组&#…...

Qt5 框架学习及应用 — 对象树
Qt 对象树 对象树概念Qt为什么使用对象树 ?将对象挂到对象树上 对象树概念 对象树:对于树的概念,相信许多学过数据结构的同学应该都不会陌生。在学习数据结构的时候我们所接触的什么二叉树、多叉树、哈夫曼树、AVL树、再到红黑树、B/B树………...

Ansible自动化运维工具---Playbook
一、playbook playbook是剧本的意思 通过 task 调用 ansible 的模块将多个 play 组织在一 个playbook中运行。 playbook本身由以下各部分组成: Tasks: 任务,即调用模块完成的某操作Variables: 变量Templates: 模板Handlers: 处理器,当某条…...

什么是接口和类?Java中的集合框架有哪些主要接口和类?
Java中的集合框架有哪些主要接口和类? Java中的集合框架(Java Collections Framework)提供了一套丰富的接口和类,用于存储和操作对象的集合。以下是Java集合框架中的主要接口和类: 主要接口 Collection: 这…...
)
算法学习笔记(最短路——Bellman-Ford)
B e l l m a n — F o r d Bellman—Ford Bellman—Ford是一种单源最短路径算法,可以用于边权为负的图,但是只能用于小图。 大概过程: 枚举每一条边,更新可以更新的节点(起点到自己距离为 0 0 0,从地点开…...

try-catch-finally的省略与springboot
在 Java 中,try-catch 块是用于捕获和处理异常的结构,它可以帮助您在代码中处理可能发生的异常情况。在某些情况下,您可能希望省略 try-catch 块并将异常向上抛出,让调用者处理异常。这种情况通常适用于以下情况: 方法…...

容器Docker:轻量级虚拟化技术解析
引言 随着云计算和虚拟化技术的飞速发展,容器技术以其轻量级、高效、可移植的特性,逐渐成为了软件开发和部署的新宠。在众多容器技术中,Docker以其简单易用、功能强大的特点,赢得了广泛的关注和应用。本文将全面介绍Docker的基本概…...

windows 系统中cuda 12.1 环境安装
文章目录 1. 安装cuda 12.11.1 下载1.2 安装 cuda1.2.1 安装步骤1.2.2 环境变量安装1.3 安装cuDNN1.3.1 安装1.3.2 cuDNN配置验证2. anaconda 安装2.1 安装2.2 环境变量配置3. 报错解决1. 安装cuda 12.1 首先通过nvidia-smi 查看可以安装的CUDA最高版本...

字节和旷视提出HiDiffusion,无需训练,只需要一行代码就可以提高 SD 生成图像的清晰度和生成速度。代码已开源。
字节和旷视提出HiDiffusion,无需训练,只需要一行代码就可以提高 SD 生成图像的清晰度和生成速度。代码已开源。 支持将图像生成的分辨率提高至40964096,同时将图像生成速度提升1.5至6倍。 支持所有 SD 模型同时也支持 SD 模型的下游模型&…...

linux下dd制作启动U盘
dd命令是比较推荐的一种Linux环境中制作U盘启动盘的方式,无需安装额外的工具,基本上所有Linux发行版都集成了这个命令。 1、插入U盘; 2、打开终端; 3、确认U盘路径,在终端中输入:sudo fdisk -l 例如&am…...

springboot整合mybatis配置多数据源(mysql/oracle)
目录 前言导入依赖坐标创建mysql/oracle数据源配置类MySQLDataSourceConfigOracleDataSourceConfig application.yml配置文件配置mysql/oracle数据源编写Mapper接口编写Book实体类编写测试类 前言 springboot整合mybatis配置多数据源,可以都是mysql数据源ÿ…...

练习项目后端代码解析切面篇(Aspect)
前言 之前注解篇时我说,通常情况下一个自定义注解一般对应一个切面,虽然项目里的切面和注解个数相同,但是好像有一个名字看起来并不对应,无所谓,先看了再说。 ExceptionLogAspect切面 我在里面做了具体注释&#x…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...
