算法学习笔记(最短路——Bellman-Ford)
B e l l m a n — F o r d Bellman—Ford Bellman—Ford是一种单源最短路径算法,可以用于边权为负的图,但是只能用于小图。
大概过程:
- 枚举每一条边,更新可以更新的节点(起点到自己距离为 0 0 0,从地点开始向外)。
- 重复第一个步骤 n − 1 n - 1 n−1次(起点不用),每一轮至少有一个节点会被更新出最短路径(和 D i j k s t r a Dijkstra Dijkstra中用到的贪心思想有点像)。
Dijkstra传送门
算法复杂度:很明显需要 n − 1 n - 1 n−1个点都需要枚举一次,每次都需要枚举 m m m条边,复杂度为 O ( n m ) O(nm) O(nm)。
同时这个算法还可以判断是否存在负环。只要更新完 n − 1 n - 1 n−1次后,还有点可以被更新最短路,那就是存在负环的,因为只有负环是每走一圈路径长度都会往下减,就可以无限更新,而正常图我们只要枚举 n − 1 n - 1 n−1遍。
也可以记录每个节点最短路的路径。(前面发过的最短路算法应该也有,可以参考 B e l l m a n F o r d Bellman_Ford BellmanFord的处理办法)
同样的,通过例题理解代码。
【模板】Bellman-Ford算法-StarryCoding | 踏出编程第一步
题目描述
n n n点 m m m边的带负权有向图(连通,可能存在重边与自环),求 1 1 1到所有点的单源最短路的距离。
保证结点 1 1 1可以到达所有结点。
如果图中存在负环,则只输出一个整数 − 1 −1 −1。
输入描述
第一行两个整数 n , m 。 ( 2 ≤ n , m ≤ 1 × 1 0 4 ) n, m。(2 \leq n , m \leq 1 \times 10^4) n,m。(2≤n,m≤1×104)
接下来 m m m行,每行一条单向边 x , y , z x,y,z x,y,z表示存在一条从 x x x到 y y y的距离为 z z z的通道。 ( 1 ≤ x , y ≤ n , − 1 0 9 ≤ z ≤ 1 0 9 ) (1 \leq x, y \leq n, -10^9 \leq z \leq 10^9) (1≤x,y≤n,−109≤z≤109)
输出描述
一行 n n n个整数,第 i i i个整数表示从点 1 1 1到点 n n n的最短距离。
如果图中存在负环,则只输出一个整数 − 1 −1 −1。
输入样例1
5 5
1 2 1
2 3 -2
3 4 1
4 5 6
1 5 -5
输出样例1
0 1 -1 0 -5
解
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 9;
using ll = long long;
const ll inf = 2e18;struct Edge
{int x;ll w;
};int n, m;
vector<Edge> g[N];
ll d[N];
//记录前驱节点,用于打印路径。
// int pre[N];void print(int s, int t) //打印路径用的
{if(s == t){cout << s << ' ';return;}print(s, pre[t])cout << t << ' ';
}void solve()
{cin >> n >> m;for(int i = 1; i <= m; ++i){int u, v;ll w; cin >> u >> v >> w;g[u].push_back({v, w});}//d[i]表示从起点到点i的距离。for(int i = 1; i <= n; ++i) d[i] = inf;d[1] = 0;bool circle; //判断负环,最后一次出来之后还是true就是一直在更新,有负环for(int i = 1; i <= n; ++i) //枚举n遍{circle = false;for(int x = 1; x <= n; ++x) //枚举每天边{for(auto [y, w] : g[x]){if(d[x] + w < d[y]) //如果能更新{d[y] = d[x] + w;// pre[x] = y; 如有需要,记录路径circle = true;}}}}if(circle) cout << "-1" << '\n';else{for(int i = 1; i <= n; ++i) cout << d[i] << ' ';}
}int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int _ = 1;while(_--) solve();return 0;
}
易错提醒:还是别忘记初始化,别忘记初始化,别忘记初始化。
P S PS PS:这个代码过不了这个例题,数据范围略大,需要优化成 s p f a spfa spfa算法。
相关文章:
)
算法学习笔记(最短路——Bellman-Ford)
B e l l m a n — F o r d Bellman—Ford Bellman—Ford是一种单源最短路径算法,可以用于边权为负的图,但是只能用于小图。 大概过程: 枚举每一条边,更新可以更新的节点(起点到自己距离为 0 0 0,从地点开…...

try-catch-finally的省略与springboot
在 Java 中,try-catch 块是用于捕获和处理异常的结构,它可以帮助您在代码中处理可能发生的异常情况。在某些情况下,您可能希望省略 try-catch 块并将异常向上抛出,让调用者处理异常。这种情况通常适用于以下情况: 方法…...

容器Docker:轻量级虚拟化技术解析
引言 随着云计算和虚拟化技术的飞速发展,容器技术以其轻量级、高效、可移植的特性,逐渐成为了软件开发和部署的新宠。在众多容器技术中,Docker以其简单易用、功能强大的特点,赢得了广泛的关注和应用。本文将全面介绍Docker的基本概…...

windows 系统中cuda 12.1 环境安装
文章目录 1. 安装cuda 12.11.1 下载1.2 安装 cuda1.2.1 安装步骤1.2.2 环境变量安装1.3 安装cuDNN1.3.1 安装1.3.2 cuDNN配置验证2. anaconda 安装2.1 安装2.2 环境变量配置3. 报错解决1. 安装cuda 12.1 首先通过nvidia-smi 查看可以安装的CUDA最高版本...

字节和旷视提出HiDiffusion,无需训练,只需要一行代码就可以提高 SD 生成图像的清晰度和生成速度。代码已开源。
字节和旷视提出HiDiffusion,无需训练,只需要一行代码就可以提高 SD 生成图像的清晰度和生成速度。代码已开源。 支持将图像生成的分辨率提高至40964096,同时将图像生成速度提升1.5至6倍。 支持所有 SD 模型同时也支持 SD 模型的下游模型&…...

linux下dd制作启动U盘
dd命令是比较推荐的一种Linux环境中制作U盘启动盘的方式,无需安装额外的工具,基本上所有Linux发行版都集成了这个命令。 1、插入U盘; 2、打开终端; 3、确认U盘路径,在终端中输入:sudo fdisk -l 例如&am…...

springboot整合mybatis配置多数据源(mysql/oracle)
目录 前言导入依赖坐标创建mysql/oracle数据源配置类MySQLDataSourceConfigOracleDataSourceConfig application.yml配置文件配置mysql/oracle数据源编写Mapper接口编写Book实体类编写测试类 前言 springboot整合mybatis配置多数据源,可以都是mysql数据源ÿ…...

练习项目后端代码解析切面篇(Aspect)
前言 之前注解篇时我说,通常情况下一个自定义注解一般对应一个切面,虽然项目里的切面和注解个数相同,但是好像有一个名字看起来并不对应,无所谓,先看了再说。 ExceptionLogAspect切面 我在里面做了具体注释&#x…...

TypeScript常见面试题第六节
题目二十六:TypeScript 中的装饰器? 一、讲解视频 TS面试题二十六:TypeScript 中的可选链? 二、题目解析 本题目考察可选链的相关知识,可选链是比较新的一个语法,是一种访问嵌套对象属性的安全的方式。即使中间的属性不存在,也不会出现错误。如果可选链 ?. 前面的值为…...

LeetCode 面试经典150题 228.汇总区间
题目: 给定一个 无重复元素 的 有序 整数数组 nums 。 返回 恰好覆盖数组中所有数字 的 最小有序 区间范围列表 。也就是说,nums 的每个元素都恰好被某个区间范围所覆盖,并且不存在属于某个范围但不属于 nums 的数字 x 。 列表中的每个区…...

大数据分析入门10分钟快速了解SQL
SQL是什么? SQL全称Structured Query Language(结构化查询语言”) 为什么要用SQL? SQL通用 常见的表格分析操作,Excel也能做,为什么不用呢? 因为处理上亿行大数据时,Excel并不够用。 而常见的大数据引…...

设置多用户远程登录windows server服务器
##设置多用户远程登录windows server服务器 ###1、远程登录windows server 2016 运行—>mstsc—>远程IP地址—>用户和密码 2、远程windows服务器设置多用户策略 运行—>gpedit.msc->计算机配置—管理模板—windows组件—远程桌面服务—远程桌面会话主机----连…...
一文了解栈
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、栈是什么?二、栈的实现思路1.顺序表实现2.单链表实现3.双向链表实现 三、接口函数的实现1.栈的定义2.栈的初始化3.栈的销毁4.入栈5.出栈6.返回栈…...
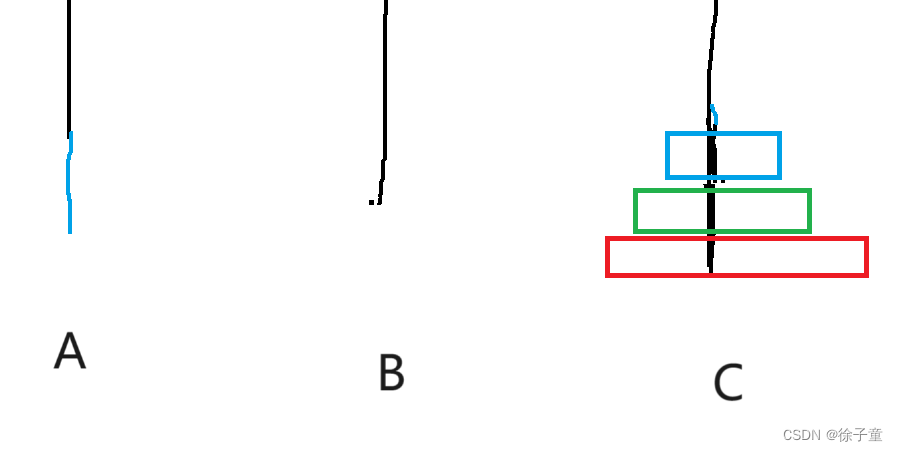
C语言----汉诺塔问题
1.什么是汉诺塔问题 简单来说,就是有三个柱子,分别为A柱,B柱,C柱。其中A柱从上往下存放着从小到大的圆盘,我们需要借助B柱和C柱,将A柱上的所有圆盘转移到C柱上,并且一次只能移动一个圆盘&#…...

Python中驼峰命名法和下划线命名法相互转换的实战代码
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...
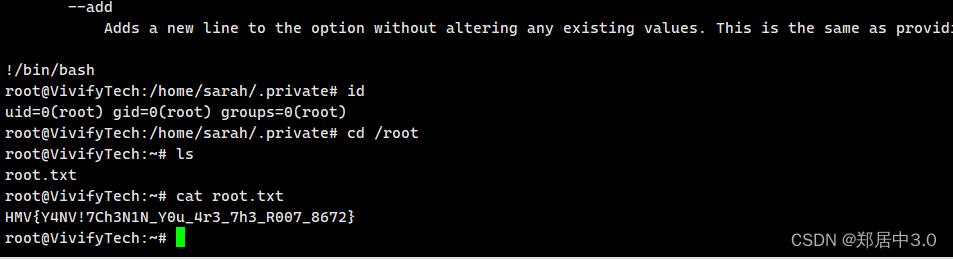
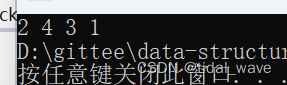
【hackmyvm】vivifytech靶机
渗透思路 信息收集端口扫描端口服务信息目录扫描爆破hydra--sshgit提权 信息收集 ┌──(kali㉿kali)-[~] └─$ fping -ag 192.168.9.0/24 2>/dev/null 192.168.9.119 --主机 192.168.9.164 --靶机个人习惯,也方便后续操作,将IP地址赋值给一个变…...

纯血鸿蒙APP实战开发——手写绘制及保存图片
介绍 本示例使用drawing库的Pen和Path结合NodeContainer组件实现手写绘制功能。手写板上完成绘制后,通过调用image库的packToFile和packing接口将手写板的绘制内容保存为图片,并将图片文件保存在应用沙箱路径中。 效果图预览 使用说明 在虚线区域手写…...

在什么情况下表单会被重复提交?如何避免?
表单被重复提交是Web应用中常见的问题,通常在用户提交表单后点击按钮多次,或在表单提交后刷新页面时发生。这可能导致数据的重复处理,比如重复记录或订单。 何时会发生表单重复提交? 用户多次点击提交按钮:在网络延迟…...

JavaScript 中的 Class 类
🔥 个人主页:空白诗 文章目录 🔥 引言🎯 基础知识🏗️ 构造函数 (Constructor)🔐 私有字段 (Private Fields)🔐 私有方法 (Private Methods)🧬 继承 (Inheritance)📦 静态…...
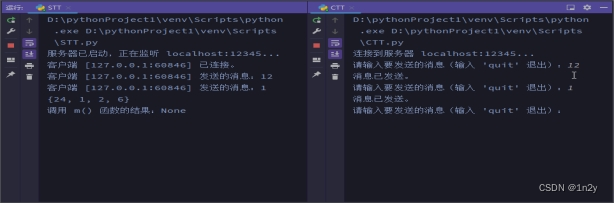
python实验三 实现UDP协议、TCP协议进行服务器端与客户端的交互
实验三 实验题目 1、请利用生成器构造一下求阶乘的函数Factorial(),定义一个函数m(),在m()中调用生成器Factorial()生成小于100的阶乘序列存入集合s中,输出s。 【代码】 def factorial():n1f1while 1: f * n yield (f) n1…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...
