题目:线性代数
问题描述:

解题思路:
列相乘,然后行相加。
注意点:由于元素数据范围最大为1e6,两个元素相乘乘积最大为1e12,如果元素类型为int则在乘的过程中就会爆炸,所以需要开long long类型。
AC代码:
#include<bits/stdc++.h>
using namespace std;const int N = 1e6 + 9;
long long a[N], b[N], ans = 0;int main()
{int n;cin >> n;for(int i = 1; i <= n; i++)cin >> a[i];for(int j = 1; j <= n; j++)cin >> b[j];for(int i = 1; i <= n; i++){ans += a[i]*b[i];}cout << ans << '\n';return 0;
}知识点:数据范围
相关文章:

题目:线性代数
问题描述: 解题思路: 列相乘,然后行相加。 注意点:由于元素数据范围最大为1e6,两个元素相乘乘积最大为1e12,如果元素类型为int则在乘的过程中就会爆炸,所以需要开long long类型。 AC代码…...
docker学习笔记3:VmWare CentOS7安装与静态ip配置
文章目录 一、安装CentOS71、下载centos镜像2、安装二、设置静态ip三、xshell连接centos本专栏的docker环境是在centos7里安装,因此首先需要会安装centos虚拟机。 本篇博客介绍如何在vm虚拟机里安装centos7。 一、安装CentOS7 1、下载centos镜像 推荐清华源,下载如下版本 …...

leetcode 547.省份数量
思路:dfs 或者这道题用bfs也是可以的。 这道题有点迷惑性,这里的数组给的是无向图的数组,而并不是地图,这里需要着重注意一下。 而后,这里的状态数组st没必要是二维的,我们并不会去遍历所给的数组&#…...

Qt5 框架学习及应用 — 对象树
Qt 对象树 对象树概念Qt为什么使用对象树 ?将对象挂到对象树上 对象树概念 对象树:对于树的概念,相信许多学过数据结构的同学应该都不会陌生。在学习数据结构的时候我们所接触的什么二叉树、多叉树、哈夫曼树、AVL树、再到红黑树、B/B树………...

Ansible自动化运维工具---Playbook
一、playbook playbook是剧本的意思 通过 task 调用 ansible 的模块将多个 play 组织在一 个playbook中运行。 playbook本身由以下各部分组成: Tasks: 任务,即调用模块完成的某操作Variables: 变量Templates: 模板Handlers: 处理器,当某条…...

什么是接口和类?Java中的集合框架有哪些主要接口和类?
Java中的集合框架有哪些主要接口和类? Java中的集合框架(Java Collections Framework)提供了一套丰富的接口和类,用于存储和操作对象的集合。以下是Java集合框架中的主要接口和类: 主要接口 Collection: 这…...
)
算法学习笔记(最短路——Bellman-Ford)
B e l l m a n — F o r d Bellman—Ford Bellman—Ford是一种单源最短路径算法,可以用于边权为负的图,但是只能用于小图。 大概过程: 枚举每一条边,更新可以更新的节点(起点到自己距离为 0 0 0,从地点开…...

try-catch-finally的省略与springboot
在 Java 中,try-catch 块是用于捕获和处理异常的结构,它可以帮助您在代码中处理可能发生的异常情况。在某些情况下,您可能希望省略 try-catch 块并将异常向上抛出,让调用者处理异常。这种情况通常适用于以下情况: 方法…...

容器Docker:轻量级虚拟化技术解析
引言 随着云计算和虚拟化技术的飞速发展,容器技术以其轻量级、高效、可移植的特性,逐渐成为了软件开发和部署的新宠。在众多容器技术中,Docker以其简单易用、功能强大的特点,赢得了广泛的关注和应用。本文将全面介绍Docker的基本概…...

windows 系统中cuda 12.1 环境安装
文章目录 1. 安装cuda 12.11.1 下载1.2 安装 cuda1.2.1 安装步骤1.2.2 环境变量安装1.3 安装cuDNN1.3.1 安装1.3.2 cuDNN配置验证2. anaconda 安装2.1 安装2.2 环境变量配置3. 报错解决1. 安装cuda 12.1 首先通过nvidia-smi 查看可以安装的CUDA最高版本...

字节和旷视提出HiDiffusion,无需训练,只需要一行代码就可以提高 SD 生成图像的清晰度和生成速度。代码已开源。
字节和旷视提出HiDiffusion,无需训练,只需要一行代码就可以提高 SD 生成图像的清晰度和生成速度。代码已开源。 支持将图像生成的分辨率提高至40964096,同时将图像生成速度提升1.5至6倍。 支持所有 SD 模型同时也支持 SD 模型的下游模型&…...

linux下dd制作启动U盘
dd命令是比较推荐的一种Linux环境中制作U盘启动盘的方式,无需安装额外的工具,基本上所有Linux发行版都集成了这个命令。 1、插入U盘; 2、打开终端; 3、确认U盘路径,在终端中输入:sudo fdisk -l 例如&am…...

springboot整合mybatis配置多数据源(mysql/oracle)
目录 前言导入依赖坐标创建mysql/oracle数据源配置类MySQLDataSourceConfigOracleDataSourceConfig application.yml配置文件配置mysql/oracle数据源编写Mapper接口编写Book实体类编写测试类 前言 springboot整合mybatis配置多数据源,可以都是mysql数据源ÿ…...

练习项目后端代码解析切面篇(Aspect)
前言 之前注解篇时我说,通常情况下一个自定义注解一般对应一个切面,虽然项目里的切面和注解个数相同,但是好像有一个名字看起来并不对应,无所谓,先看了再说。 ExceptionLogAspect切面 我在里面做了具体注释&#x…...

TypeScript常见面试题第六节
题目二十六:TypeScript 中的装饰器? 一、讲解视频 TS面试题二十六:TypeScript 中的可选链? 二、题目解析 本题目考察可选链的相关知识,可选链是比较新的一个语法,是一种访问嵌套对象属性的安全的方式。即使中间的属性不存在,也不会出现错误。如果可选链 ?. 前面的值为…...

LeetCode 面试经典150题 228.汇总区间
题目: 给定一个 无重复元素 的 有序 整数数组 nums 。 返回 恰好覆盖数组中所有数字 的 最小有序 区间范围列表 。也就是说,nums 的每个元素都恰好被某个区间范围所覆盖,并且不存在属于某个范围但不属于 nums 的数字 x 。 列表中的每个区…...

大数据分析入门10分钟快速了解SQL
SQL是什么? SQL全称Structured Query Language(结构化查询语言”) 为什么要用SQL? SQL通用 常见的表格分析操作,Excel也能做,为什么不用呢? 因为处理上亿行大数据时,Excel并不够用。 而常见的大数据引…...

设置多用户远程登录windows server服务器
##设置多用户远程登录windows server服务器 ###1、远程登录windows server 2016 运行—>mstsc—>远程IP地址—>用户和密码 2、远程windows服务器设置多用户策略 运行—>gpedit.msc->计算机配置—管理模板—windows组件—远程桌面服务—远程桌面会话主机----连…...
一文了解栈
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、栈是什么?二、栈的实现思路1.顺序表实现2.单链表实现3.双向链表实现 三、接口函数的实现1.栈的定义2.栈的初始化3.栈的销毁4.入栈5.出栈6.返回栈…...
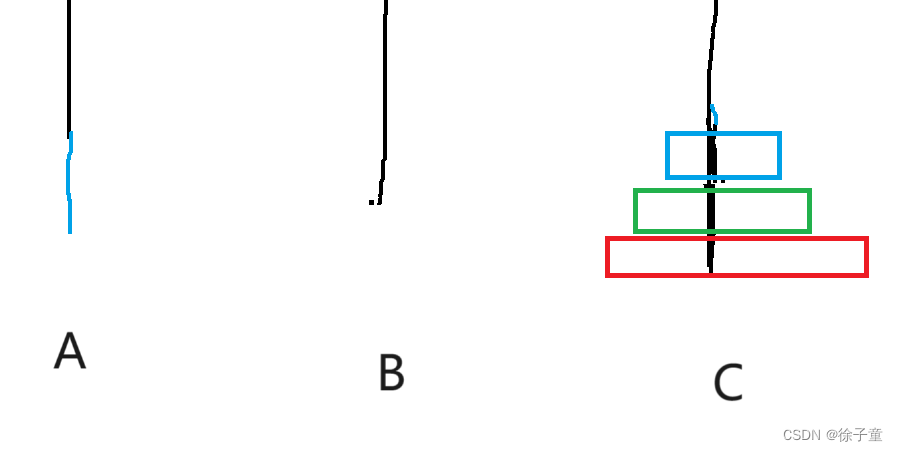
C语言----汉诺塔问题
1.什么是汉诺塔问题 简单来说,就是有三个柱子,分别为A柱,B柱,C柱。其中A柱从上往下存放着从小到大的圆盘,我们需要借助B柱和C柱,将A柱上的所有圆盘转移到C柱上,并且一次只能移动一个圆盘&#…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...
