UVA1048/LA3561 Low Cost Air Travel
UVA1048/LA3561 Low Cost Air Travel
- 题目链接
- 题意
- 输入格式
- 输出格式
- 分析
- AC 代码
题目链接
本题是2006年ICPC世界总决赛的A题
题意
很多航空公司都会出售一种联票,要求从头坐,上飞机时上缴机票,可以在中途任何一站下飞机。比如,假设你有一张“城市1->城市2->城市3”的联票,你不能用来只从城市2飞到城市3(因为必须从头坐),也不能先从城市1飞到城市2再用其他票飞到其他城市玩,回到城市2后再用原来的机票飞到城市3(因为机票已经上缴)。
这里有一个例子。假设有3种票,每种票的情况如下所示:
∙ \bullet ∙ 票1:城市1->城市3->城市4,票价225美元
∙ \bullet ∙ 票2:城市1->城市2,票价200美元
∙ \bullet ∙ 票3:城市2->城市3,票价50美元
你想从城市1飞到城市3,有两种方法可以选择。买票1,只飞第一段;买票2和3,通过城市2中转。显然,第一种方法比较省钱,虽然浪费了一段。
给出票的信息,以及一个或多个行程单,你的任务是买尽量少的票(同一种票可以买多张),使得总花费最小。输入保证行程总是可行的。行程单上的城市必须按顺序到达,但中间可以经过一些辅助城市。
输入格式
输入包含多组数据。每组数据第一行为一个整数NT,即联票的种类数。以下NT行每行为一个联票描述,其中第一个整数为票的价格,然后是联票上城市的数目以及这些城市的整数编号(按顺序给出)。接下来为一个整数NI,即需要计算最小花费的行程单数目。以下NI行每行为一个行程单,其中一个整数为行程单上的城市数目(包括起始城市),以及这些城市的编号(按顺序给出,每个城市编号可取任意整数但唯一)。输入保证每组数据最多包含20种联票和20个行程单,每张票或者行程单上有至少2个,最多10个城市。票价不超过$10000。联票或者行程单上的相邻城市保证不同。票和行程单都从1开始编号。输入结束标志为NT=0。
输出格式
对于每组数据的每张行程单,输出最小花费和对应的方案(按顺序,详见样例输出)。输出保证唯一。
分析
题目交代每个城市的编号是任意整数但唯一,因此需要对城市重新编号(不同城市最多200个)。行程单上的城市必须按顺序到达,但中间可以经过一些辅助城市,这里其实隐含了一点:只能从行程单的首个城市作为初始出发点。
充分理解题意之后,可以知道本题其实是单源最短路问题,可以用spfa处理,只不过需要重新定义状态点:d[i][j]表是当前旅行到了城市i,已经走完行程单前j个城市的最小花费。
可以用结构体struct {int v, k, t;} ans[N][M]记录最短路径:ans[i][j]记录当前旅行到了城市i,已经走完行程单前j个城市花费最小时,上个行程旅行到了城市v,已经走完行程单前k个城市,对应转机的机票t。
AC 代码
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;#define T 21
#define M 11
#define N 202
int d[N][M], f[N][M], a[T][M], w[T], c[T], b[M], id[N], m, n, t, x, kase = 0;
struct node {int v, k;} p; struct {int v, k, i;} ans[N][M];int find(int v) {for (int i=0; i<x; ++i) if (id[i] == v) return i;id[x] = v;return x++;
}int bfs() {cin >> m;for (int i=0, v; i<m; ++i) cin >> v, b[i] = find(v);memset(d, 1, sizeof(d)); memset(f, 0, sizeof(f)); queue<node> q;for (int i=1; i<=t; ++i) if (a[i][0] == b[0]) for (int j=1, k=1, v; j<c[i] && k<m; ++j) {if ((v = a[i][j]) == b[k]) ++k;if (w[i] < d[v][k]) {d[v][k] = w[i]; ans[v][k] = {0, 0, i};if (k<m && !f[v][k]) q.push({v, k}), f[v][k] = 1;}}while (!q.empty()) {p = q.front(); q.pop();int v0 = p.v, k0 = p.k, g = d[v0][k0]; f[v0][k0] = 0;for (int i=1; i<=t; ++i) if (a[i][0] == v0) for (int j=1, k=k0, v; j<c[i] && k<m; ++j) {if ((v = a[i][j]) == b[k]) ++k;if (g + w[i] < d[v][k]) {d[v][k] = g + w[i]; ans[v][k] = {v0, k0, i};if (k<m && !f[v][k]) q.push({v, k}), f[v][k] = 1;}}}return d[b[m-1]][m];
}void path(int v, int k) {if (ans[v][k].k) path(ans[v][k].v, ans[v][k].k);cout << ' ' << ans[v][k].i;
}void solve() {x = 0;for (int i=1; i<=t; ++i) {cin >> w[i] >> c[i];for (int j=0, v; j<c[i]; ++j) cin >> v, a[i][j] = find(v);}cin >> n; ++kase;for (int i=1; i<=n; ++i) {cout << "Case " << kase << ", Trip " << i << ": Cost = " << bfs() << endl << " Tickets used:";path(b[m-1], m); cout << endl;}
}int main() {while (cin >> t && t) solve();return 0;
}
相关文章:

UVA1048/LA3561 Low Cost Air Travel
UVA1048/LA3561 Low Cost Air Travel 题目链接题意输入格式输出格式 分析AC 代码 题目链接 本题是2006年ICPC世界总决赛的A题 题意 很多航空公司都会出售一种联票,要求从头坐,上飞机时上缴机票,可以在中途任何一站下飞机。比如,假…...
学习和分析各种数据结构所要掌握的一个重要知识——CPU的缓存利用率(命中率)
什么是CPU缓存利用率(命中率),我们首先要把内存搞清楚。 硬盘是什么,内存是什么,高速缓存是什么,寄存器又是什么? 我们要储存数据就要运用到上面的东西。首先里面的硬盘是可以无电存储的&#…...

IOS自动化—将WDA打包ipa批量安装驱动
前言 CSDN: ios自动化-Xcode、WebDriverAgent环境部署 ios获取原生系统应用的包 如果Mac电脑没有配置好Xcode相关环境,可以参考以上文章。 必要条件 Mac电脑,OS版本在12.4及以上(低于这个版本无法安装Xcode14,装不了Xcode14就…...
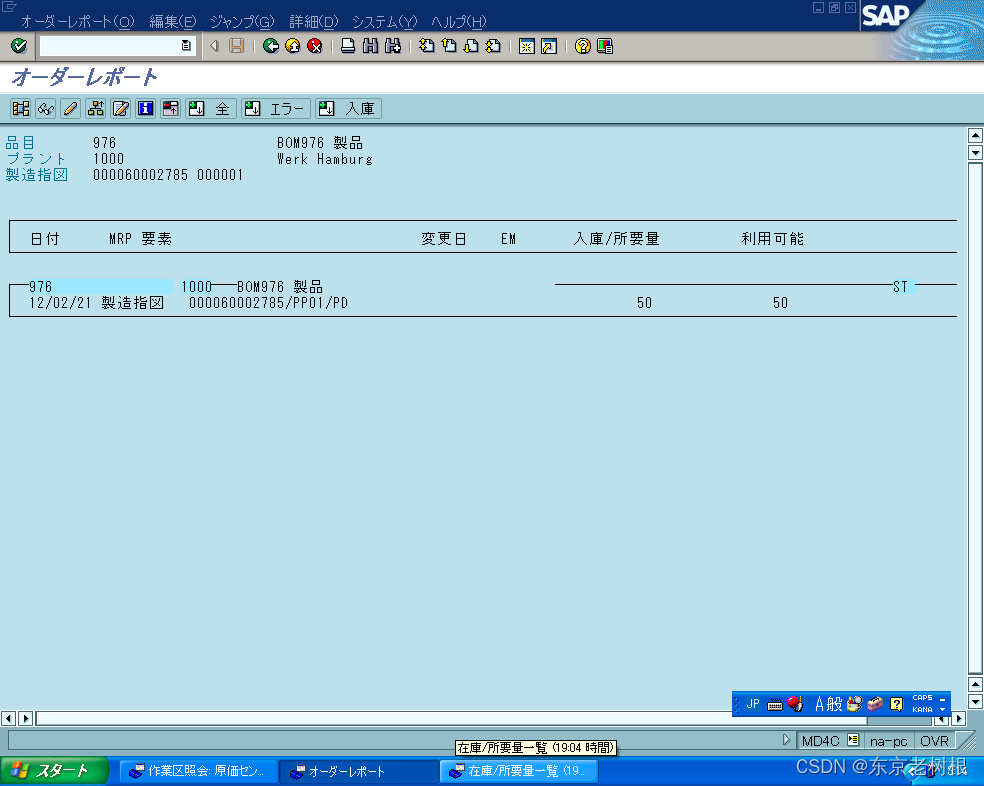
SAP PP学习笔记12 - 评估MRP的运行结果
上一章讲了MRP的概念,参数,配置等内容。 SAP PP学习笔记11 - PP中的MRP相关概念,参数,配置-CSDN博客 本章来讲 MRP跑完之后呢,要怎么评估这个MRP的运行结果。 1,Stock/Requirements List and MRP List 在…...
AndroidStudio的Iguana版的使用
1.AndroidStudio介绍 Android Studio 是用于开发 Android 应用的官方集成开发环境 (IDE)。Android Studio 基于 IntelliJ IDEA 强大的代码编辑器和开发者工具,还提供更多可提高 Android 应用构建效率的功能,例如: 基于 Gradle 的灵活构建系统…...

通过方法引用获取属性名的底层逻辑是什么?
很多小伙伴可能都用过 MyBatis-Plus,这里边我们构造 where 条件的时候,可以直接通过方法引用的方式去指定属性名: LambdaQueryWrapper<Book> qw new LambdaQueryWrapper<>(); qw.eq(Book::getId, 2); List<Book> list bo…...

自学错误合集--项目打包报错,运行报错持续更新中
java后端自学错误总结 一.项目打包报错2.项目打包之后运行报错 二.项目运行报错 一.项目打包报错 javac: �Ҳ����ļ�: E:\xx\xx\xx\docer-xx\src\main\java\xx\xx\xx\xx\xx\xx.java �ÿ…...
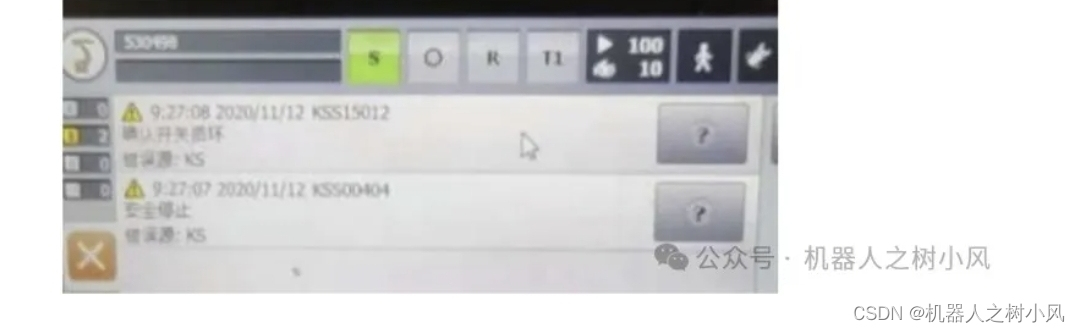
KUKA机器人故障报警信息处理(一)
1、KSS00276 机器人参数不等于机器人类型 ①登录专家模式 ②示教器操作:【菜单】—【显示】—【变量】—【单个】 ③名称输入:$ROBTRAFO[] 新值:TRAFONAME[] ④点击【设定值】。 2、电池报警: ①“充电电池警告-发现老化的蓄电池…...
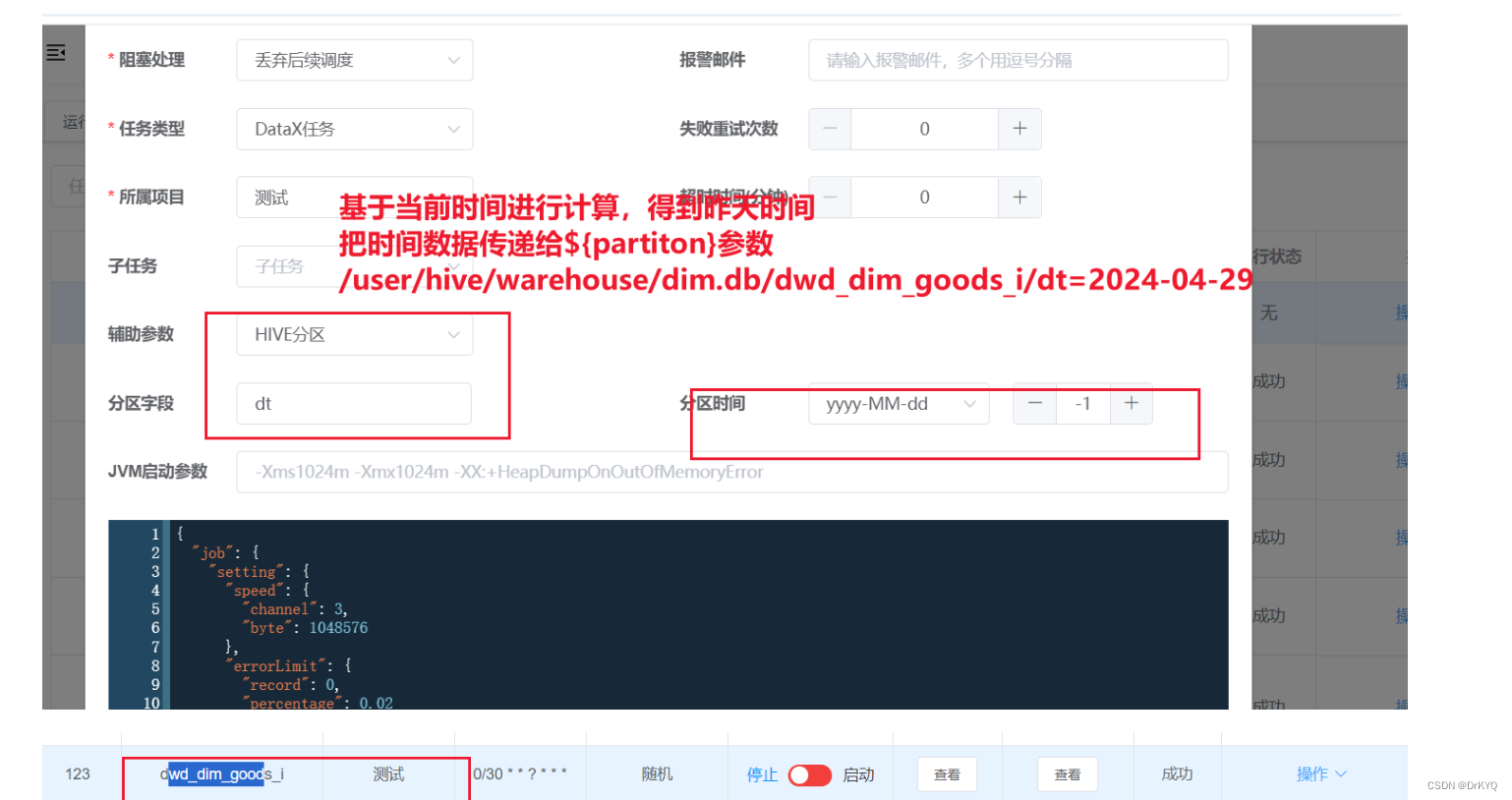
数仓开发:DIM层数据处理
一、了解DIM层 这个就是数仓开发的分层架构 我们现在是在DIM层,从ods表中数据进行加工处理,导入到dwd层,但是记住我们依然是在DIM层,而非是上面的ODS和DWD层。 二、处理维度表数据 ①先确认hive的配置 -- 开启动态分区方案 -- …...
echars设置渐变颜色的方法
在我们日常的开发中,难免会遇到有需求,需要使用echars设置渐变的图表,如果我们需要设置给图表设置渐变颜色的话,我们只需要在 series 配置项中 添加相应的属性配置项即可。 方式一:colorStops type:‘lin…...
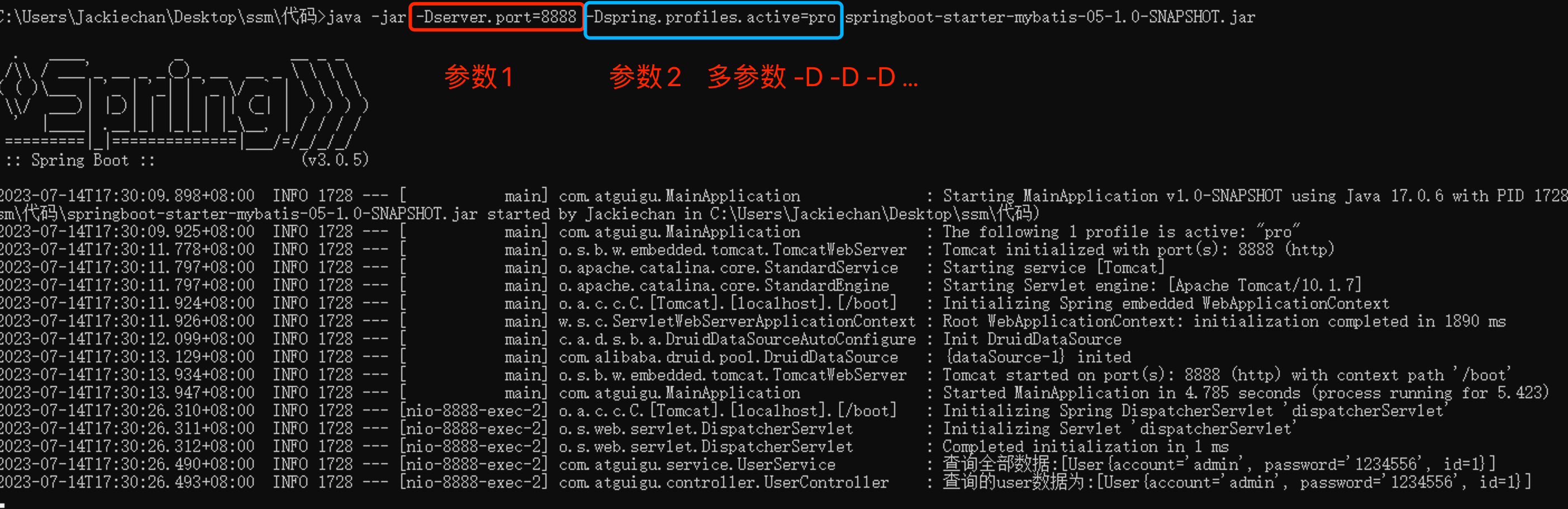
SpringBoot3项目打包和运行
六、SpringBoot3项目打包和运行 6.1 添加打包插件 在Spring Boot项目中添加spring-boot-maven-plugin插件是为了支持将项目打包成可执行的可运行jar包。如果不添加spring-boot-maven-plugin插件配置,使用常规的java -jar命令来运行打包后的Spring Boot项目是无法找…...

Spring Cloud Gateway的部署
不要将 Spring Cloud Gateway 部署到 Tomcat 可以将Spring Cloud Gateway打成jar包,并通过jar包部署,步骤: 1. 修改构建配置 确保你的pom.xml文件中的打包方式为jar。 <packaging>jar</packaging> 2 打包项目 mvn clean pack…...

算法提高之树的最长路径
算法提高之树的最长路径 核心思想:树形dp 枚举路径的中间节点用f1[i] 表示i的子树到i的最长距离,f2[i]表示次长距离最终答案就是max(f1[i]f2[i]) #include <iostream>#include <cstring>#include <algorithm>using namespace std;const int N …...
git/gerrit使用遇到的问题
Push时出现的多个问题及其解决 branch【...】not found 这个错误通常出现在 Git 命令中指定的分支名称中包含特殊字符或者语法错误时。需要确保指定的分支名称是正确的,并且没有任何不支持的字符。 例如,如果分支名称是 feature/branch,应该…...

机器学习第二天(监督学习,无监督学习,强化学习,混合学习)
1.是什么 基于数据寻找规律从而建立关系,进行升级,如果是以前的固定算式那就是符号学习了 2.基本框架 3.监督学习和无监督式学习: 监督学习:根据正确结果进行数据的训练; 在监督式学习中,训练数据包括输…...

Rust 解决循环引用
导航 循环引用一、现象二、解决 循环引用 循环引用出现的一个场景就是你指向我,我指向你,导致程序崩溃 解决方式可以通过弱指针,而Rust中的弱指针就是Weak 在Rc中,可以实现,对一个变量,持有多个不可变引…...

ICC2:如何解决pin density过高引起的绕线问题
我正在「拾陆楼」和朋友们讨论有趣的话题,你⼀起来吧? 拾陆楼知识星球入口 为了追求极致的利用率,综合往往会使用大量的AOI/OAI等多pin cell,然而后端实现过程中,工具为了解决绕线难题,又会通过降低local density的方法实现反向奔赴,即便如此,绕线后仍会残留不少问题,…...

Buuctf-Misc题目练习
打开后是一个gif动图,可以使用stegsolve工具进行逐帧看。 File Format:文件格式 Data Extract:数据提取 Steregram Solve:立体试图 可以左右控制偏移 Frame Browser:帧浏览器 Image Combiner:拼图,图片拼接 所以可以知道我们要选这个Frame Browser …...

费马小定理详解
费马小定理 定义: 设 p 为素数,a 为整数,则 a p ≡ a ( m o d p ) a^p \equiv a\ (\mod p) ap≡a (modp) ,若 p ∤ a p \nmid a p∤a ,则 a p − 1 ≡ 1 ( m o d p ) a^{p-1} \equiv 1\ (\mod p) ap−1≡1 (modp)…...

PXE批量安装
系统装机的三种引导方式 u盘光盘网络装机 光盘: 1.类似于usb模式 2.刻录模式 系统安装过程 加载boot loader Boot Loader 是在操作系统内核运行之前运行的一段小程序。通过这段小程序,我们可以初始化硬件设备、建立内存空间的映射图,从…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...
