【拆位法 决策包容性 位运算】2871. 将数组分割成最多数目的子数组
本文涉及知识点
拆位法 贪心 位运算 决策包容性
位运算、状态压缩、子集状态压缩汇总
LeetCode2871. 将数组分割成最多数目的子数组
给你一个只包含 非负 整数的数组 nums 。
我们定义满足 l <= r 的子数组 nums[l…r] 的分数为 nums[l] AND nums[l + 1] AND … AND nums[r] ,其中 AND 是按位与运算。
请你将数组分割成一个或者更多子数组,满足:
每个 元素都 只 属于一个子数组。
子数组分数之和尽可能 小 。
请你在满足以上要求的条件下,返回 最多 可以得到多少个子数组。
一个 子数组 是一个数组中一段连续的元素。
示例 1:
输入:nums = [1,0,2,0,1,2]
输出:3
解释:我们可以将数组分割成以下子数组:
- [1,0] 。子数组分数为 1 AND 0 = 0 。
- [2,0] 。子数组分数为 2 AND 0 = 0 。
- [1,2] 。子数组分数为 1 AND 2 = 0 。
分数之和为 0 + 0 + 0 = 0 ,是我们可以得到的最小分数之和。
在分数之和为 0 的前提下,最多可以将数组分割成 3 个子数组。所以返回 3 。
示例 2:
输入:nums = [5,7,1,3]
输出:1
解释:我们可以将数组分割成一个子数组:[5,7,1,3] ,分数为 1 ,这是可以得到的最小总分数。
在总分数为 1 的前提下,最多可以将数组分割成 1 个子数组。所以返回 1 。
提示:
1 <= nums.length <= 105
0 <= nums[i] <= 106
位运算、贪心
因为 x&y <= x+y ,所以只分成一个子数组,一定分数和最小。
拆位法,如果某个二进制位全部为1,则分成一个子数组,结果为1。分成两个或更大,结果一定大于1。
如果任何一个二进制位全部是1,则只能分成一个子数组。
如果所有二进制位不全为1,则结果一定为0。即所有子数组的分数必须为0。
决策包容性
假定nums[l…r1]积分为0,nums[l…r2]积分也为0,r1 < r2。那么选择nums[l…r1]。
假定后者:nums[l…r2] ,nums[r2+1…r3] ⋯ \cdots ⋯ 则nums[l…r1] ,nums[r1+1,r3] ⋯ \cdots ⋯也符合。x&y 的结果 不会大于x或y。
代码
核心代码
class Solution {
public:int maxSubarrays(vector<int>& nums) {int iRet = 0 ;int iAnd = -1;for (int i = 0; i < nums.size();i++ ) {iAnd &= nums[i];if (0 == iAnd) {iRet++;iAnd = -1;}}if (0 == iRet) { return 1; }return iRet ;}
};
测试用例
template<class T>
void Assert(const vector<T>& v1, const vector<T>& v2)
{if (v1.size() != v2.size()){assert(false);return;}for (int i = 0; i < v1.size(); i++){assert(v1[i] == v2[i]);}
}template<class T>
void Assert(const T& t1, const T& t2)
{assert(t1 == t2);
}int main()
{vector<int> nums;{Solution slu;nums = { 1,0,2,0,1,2 };auto res = slu.maxSubarrays(nums);Assert(3, res);}{Solution slu;nums = { 5,7,1,3 };auto res = slu.maxSubarrays(nums);Assert(1, res);}
}

扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【拆位法 决策包容性 位运算】2871. 将数组分割成最多数目的子数组
本文涉及知识点 拆位法 贪心 位运算 决策包容性 位运算、状态压缩、子集状态压缩汇总 LeetCode2871. 将数组分割成最多数目的子数组 给你一个只包含 非负 整数的数组 nums 。 我们定义满足 l < r 的子数组 nums[l…r] 的分数为 nums[l] AND nums[l 1] AND … AND nums[r…...

Java 线程池 ( Thread Pool )的简单介绍
想象一下,你正指挥着一支超级英雄团队,面对蜂拥而至的敌人(任务),不是每次都召唤新英雄(创建线程),而是精心调配现有成员,高效应对。这就是Java线程池的魔力,…...

鸿蒙内核源码分析(时间管理篇) | 谁是内核基本时间单位
时间概念太重要了,在鸿蒙内核又是如何管理和使用时间的呢? 时间管理以系统时钟 g_sysClock 为基础,给应用程序提供所有和时间有关的服务。 用户以秒、毫秒为单位计时.操作系统以Tick为单位计时,这个认识很重要. 每秒的tick大小很大程度上决…...

安装numpy遇到的问题
安装numpy的时候提示无法安装如下: (venv) E:\works\AI\venv\Scripts>pip install numpy pandas matplotlib jupyter -i https://pypi.douban.com/simple Looking in indexes: https://pypi.douban.com/simple WARNING: Retrying (Retry(total4, connectNone, r…...

页面嵌套,界面套娃,除了用iframe,还有其他方式吗?
UIOTOS可以了解下,uiotos.net,通过连线来代替脚本逻辑开发,复杂的交互界面,通过页面嵌套轻松解决,是个很新颖的思路,前端零代码! 蓝图连线尤其是独创的页面嵌套和属性继承技术,好家…...
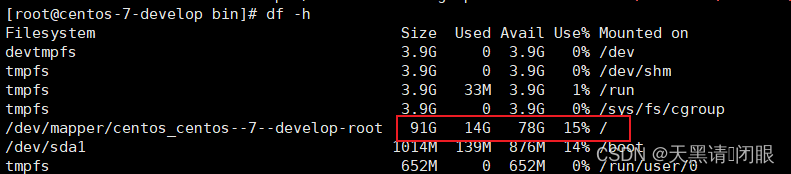
上传文件至linux服务器失败
目录 前言异常排查使用df -h命令查看磁盘使用情况使用du -h --max-depth1命令查找占用空间最大的文件夹 原因解决补充:删除文件后,磁盘空间无法得到释放 前言 使用XFTP工具上传文件至CentOS服务器失败 异常 排查 使用df -h命令查看磁盘使用情况 发现磁盘…...

渗透 如何防御ARP欺骗,LLMNR-MDNS-NBNS等协议的作用
一. 如何防御ARP欺骗? 1.使用双向IP/MAC绑定; 2.使用静态ARP缓存表; 3.使用ARP服务器,通过服务器来查找ARP转换表来响应其他机器的广播; 4.使用ARP欺骗防护软件; 5.在网关设备上部署防ARP欺骗攻击功能…...

【C++ 所有STL容器简介】
【C 所有STL容器简介】 1. vector2. list3. deque4. set / multiset5. map / multimap6. unordered_set / unordered_multiset7. unordered_map / unordered_multimap8. stack9. queue10. priority_queue C 标准模板库(STL)提供了一系列常用的容器&#…...

Django调用SECRET_KEY对数据进行加密
对数据进行加密 在Django中进行加密可以直接调用django配置文件中的SECRET_KEY , 同时还需要导入itsdangerous模块中的TimedJSONWebSignatureSerializer进行加密 1. 实现加密方法 , 生成用户加密链接 # 生成用户加密链接 def generate_verify_email_url(user):# 调研加密方法…...
芸众商城电商专业版400+插件源码+搭建教程
介绍: 芸众商城社交电商系统SAAS平台前端基于vue开发,后端基于研发积分商城系统源码 php,本文安装芸众商城全插件(400多个)商业版平台源码,可同时支持多端口部署运行;使用宝塔面板一键部署的形…...

【机器学习与实现】线性回归示例——波士顿房价分析
目录 一、创建Pandas对象并查看数据的基本情况二、使用皮尔逊相关系数分析特征之间的相关性三、可视化不同特征与因变量MEDV(房价中值)间的相关性四、划分训练集和测试集并进行回归分析 一、创建Pandas对象并查看数据的基本情况 boston.csv数据集下载&a…...

Redis核心数据结构——跳表(生成数据到文件和从文件中读取数据、模块合并、)
生成文件和从文件中读取数据。 需求如下: 你的任务是实现 SkipList 类中的数据持久化成员函数和数据加载成员函数。 持久化数据成员函数签名:void dump_file(); 该成员函数负责将存储引擎内的数据持久化到文件中。数据的持久化格式是将每个键值对写入文…...

微信小程序下载文件详解
在微信小程序中,下载文件通常涉及使用 wx.downloadFile API。这个 API 可以将网络资源下载到本地临时文件路径,然后你可以使用 wx.saveFile 将临时文件保存到本地持久存储位置。下面是一个下载文件的详细过程: 使用 wx.downloadFile 下载文件…...

2024 概率论和数理统计/专业考试/本科考研/论文/重点公式考点汇总
## 列表http://www.deepnlp.org/equation/category/statistics ## 均匀分布http://www.deepnlp.org/equation/uniform-distribution ## t-分布http://www.deepnlp.org/equation/student-t-distribution ## 伯努利分布http://www.deepnlp.org/equation/bernoulli-distributio…...

四川易点慧电子商务抖音小店:潜力无限的新零售风口
在当今数字化浪潮中,电子商务已经成为推动经济发展的重要引擎。四川易点慧电子商务有限公司凭借其敏锐的市场洞察力和创新精神,成功在抖音小店这一新兴平台上开辟出一片新天地。本文将探讨四川易点慧电子商务抖音小店的潜力及其在新零售领域的影响力。 一…...

Seal^_^【送书活动第3期】——《Hadoop大数据分析技术》
Seal^_^【送书活动第3期】——《Hadoop大数据分析技术》 一、参与方式二、作者荐语三、图书简介四、本期推荐图书4.1 前 言4.2 本书内容4.3 本书目的4.4 本书适合的读者4.5 配套源码、PPT课件等资源下载 五、目 录六、🛒 链接直达 Hadoop框架入门书,可当…...
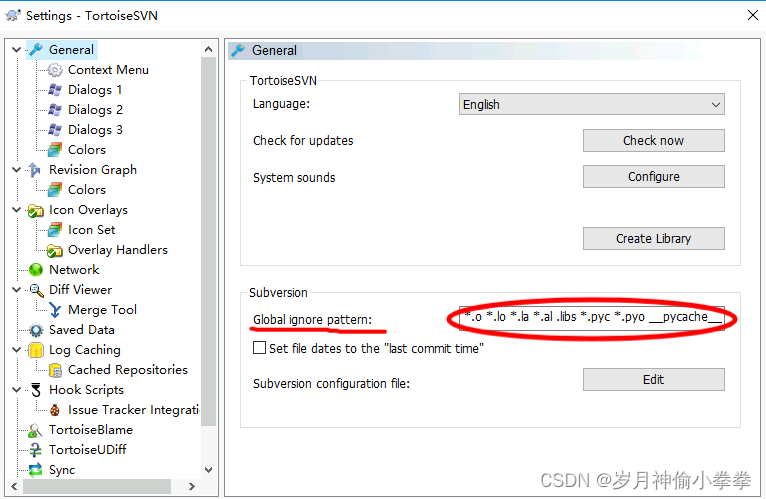
win10下,svn上传.so文件失败
问题:win10下使用TortoiseSVN,svn上传.so文件失败 解决:右键,选择Settings,Global ignore pattern中删除*.so,保存即可。...
ubuntu20安装colmap
系统环境 ubuntu20 ,cuda11.8 ,也安装了anaconda。因为根据colmap的官方文档说的,如果根据apt-get安装的话,默认是非cuda版本的,而我觉得既然都安装了cuda11.8了,自然也要安装cuda版本的colmap。 安装步骤…...
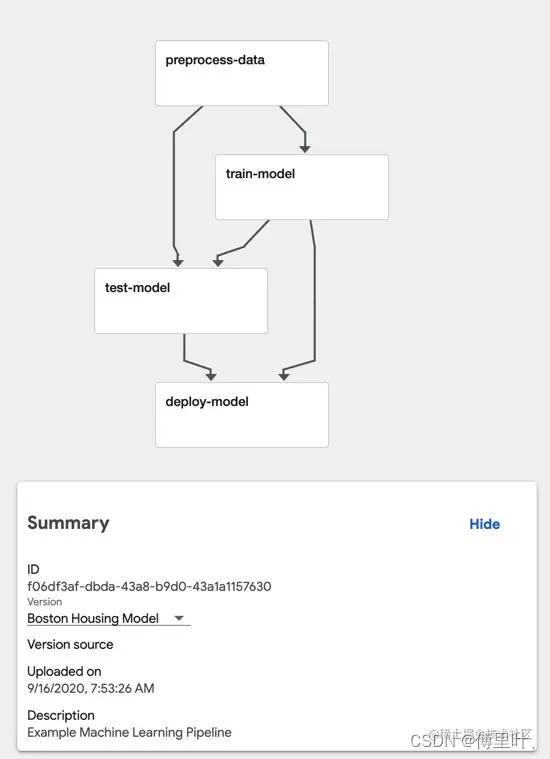
kubeflow简单记录
kubeflow 13.7k star 1、Training Operator 包括PytorchJob和XGboostJob,支持部署pytorch的分布式训练 2、KFServing快捷的部署推理服务 3、Jupyter Notebook 基于Web的交互式工具 4、Katib做超参数优化 5、Pipeline 基于Argo Workflow提供机器学习流程的创建、编排…...

ARM的工作模式
ARM处理器设计有七种工作模式,这些模式允许处理器在不同的情境下以不同的权限级别执行任务,下面是这七大工作模式的概述: 用户模式(User,USR): 这是非特权模式,大多数应用程序在此…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...
