【C++历练之路】红黑树——map与set的封装实现

W...Y的个人主页💕
gitee代码仓库分享😊
前言:上篇博客中,我们为了使二叉搜索树不会出现”一边倒“的情况,使用了AVL树对搜索树进行了处理,从而解决了数据在有序或者接近有序时出现的情况。但是AVL树还会有一大缺陷就是其性能的原因,当我们在使其满足AVL树的规则时,其付出的旋转代价是非常大的,所以经常修改的结构就不适合AVL树。但是红黑树就可以补足AVL树的缺陷。
目录
1. 红黑树
1.1 红黑树的概念
1.2 红黑树的性质
1.3红黑树节点的定义
1.4红黑树的插入
1.5 红黑树与AVL树的比较
2. 红黑树模拟实现STL中的map与set
2.1 红黑树的迭代器
2.2 红黑树的改写与迭代器完整代码
2.3 map的封装
2.4 set的封装
1. 红黑树
1.1 红黑树的概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或
Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路
径会比其他路径长出俩倍,因而是接近平衡的。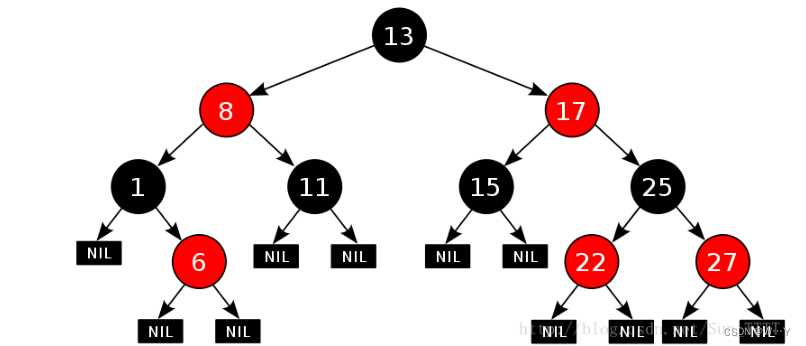
假设最短路径为h,则最长路径为2h。
1.2 红黑树的性质
1. 每个结点不是红色就是黑色
2. 根节点是黑色的
3. 如果一个节点是红色的,则它的两个孩子结点必须是黑色的
4. 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均 包含相同数目的黑色结点
5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
为什么满足上述性质,红黑树就可以保证其最长路径的节点树不会超过最短路径的两倍呢?
前两个性质非常通俗易懂,我们从第三个性质开始解读:
3.没有连续的两个红色节点。
4.每条路径的黑色节点数是相同的。
所以我们就可以假设一颗红黑树中每条路径有两个黑色节点(满足性质4),那最短路径只可能是全黑节点,最长路径一定是一黑一红节点(假设最短路径与最长路径都存在),那么红色节点只能在黑色节点中间插入,这样才能满足性质3,所以红黑树就可以保证其最长路径的节点树不会超过最短路径的两倍。
对比AVL树与红黑树的结构,其AVL树的高度近似logN,而红黑树的高度近似2logN,所以相对于AVL树,红黑树的搜索效率差一些,但是几乎可以忽略不计,因为logN足够小,所以他们之间的搜索差距微乎其微。
1.3红黑树节点的定义
enum Colour
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv),_col(RED){}
};在节点定义时我们默认将节点设置成红色节点,这样如果出现连续的红色节点时,我们可以进行变色操作,通过维护一个子树来使红黑树合法,但是如果插入一个黑色节点时,我们就无法下手,因为每条路的黑色节点数必须相同,这样我们无法很好的进行操作使其合法化。
1.4红黑树的插入
红黑树是在二叉搜索树的基础上加上其平衡限制条件,因此红黑树的插入可分为两步:
1. 按照二叉搜索的树规则插入新节点:
class RBTree
{typedef RBTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv); // 红色的if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;
}
private:Node* _root = nullptr;
};
2. 检测新节点插入后,红黑树的性质是否造到破坏:
因为新节点的默认颜色是红色,因此:如果其双亲节点的颜色是黑色,没有违反红黑树任何
性质,则不需要调整;但当新插入节点的双亲节点颜色为红色时,就违反了性质三不能有连
在一起的红色节点,此时需要对红黑树分情况来讨论:
约定:cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点
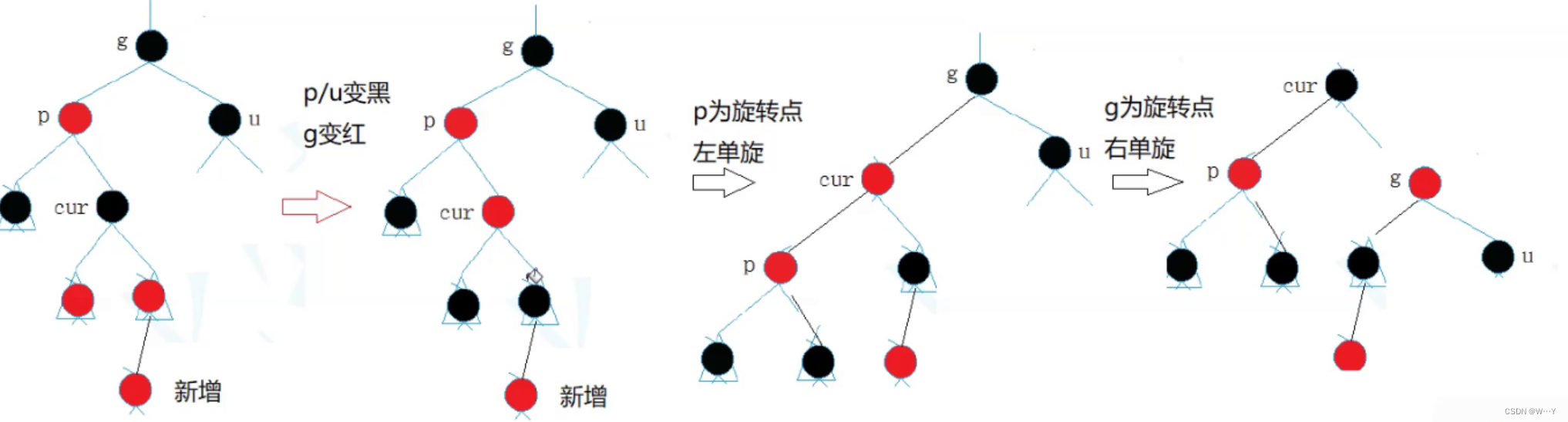
情况一: cur为红,p为红,g为黑,u存在且为红
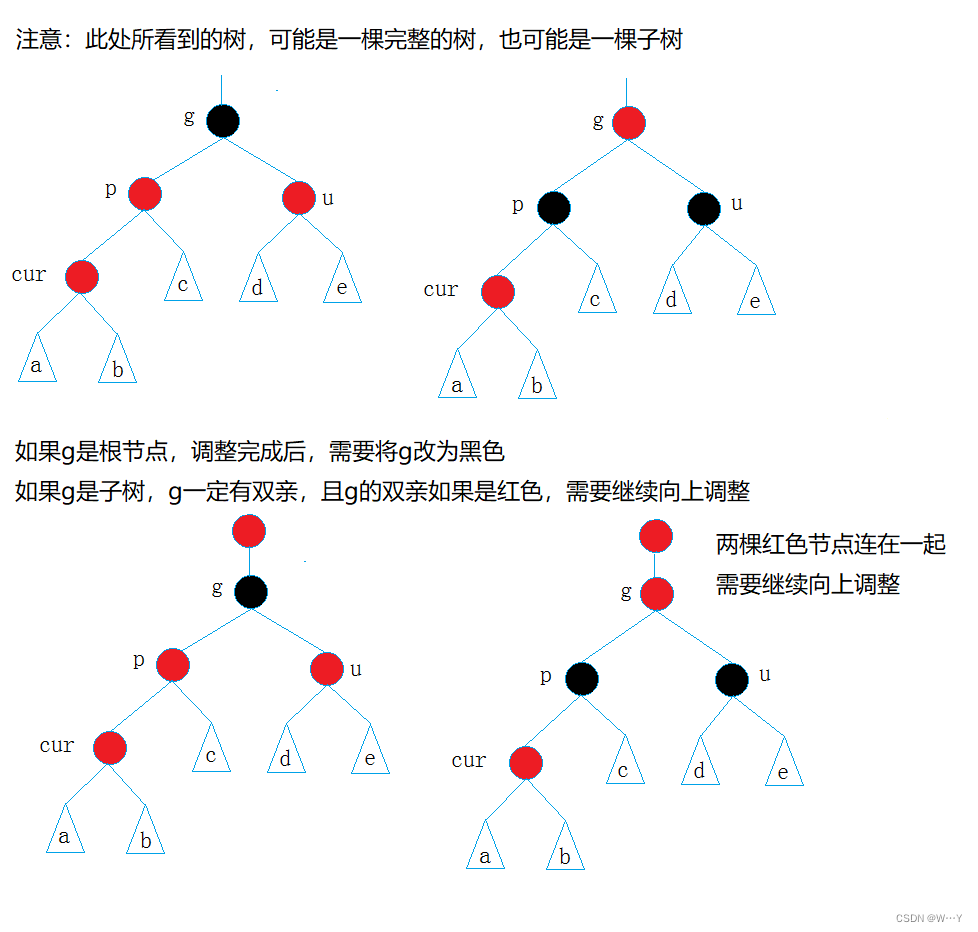
解决方式:将p,u改为黑,g改为红,然后把g当成cur,继续向上调整。
情况二: cur为红,p为红,g为黑,u不存在/u存在且为黑
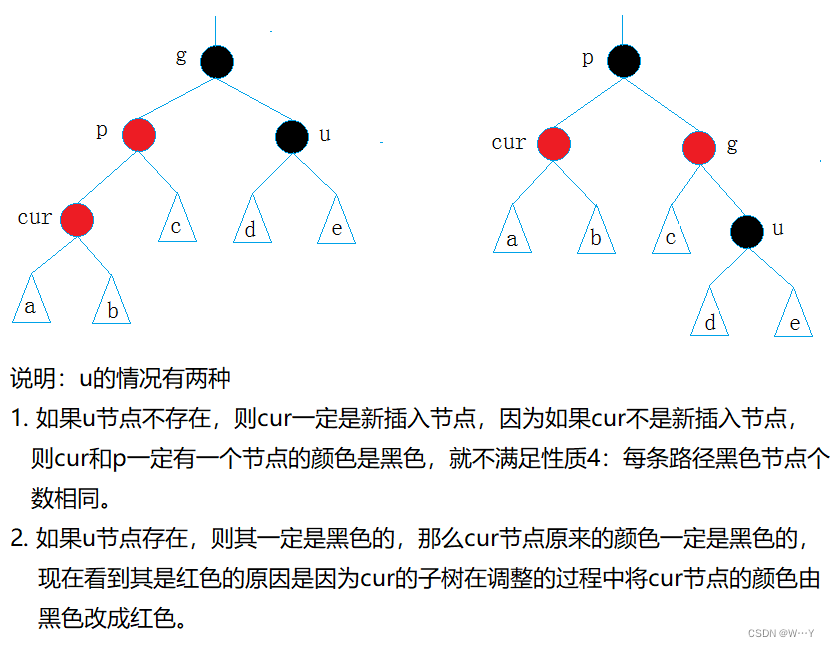
如果u存在且为黑, 则cur一定不是新增节点,因为这样就不满足性质4:每条路径黑色节点个数相同。所以我们将上面图补充完整就是下图所示,先是由情况一进行调整,然后向上调整后才得到上图。所以情况一向上调整后的情况不一定又是情况一!!
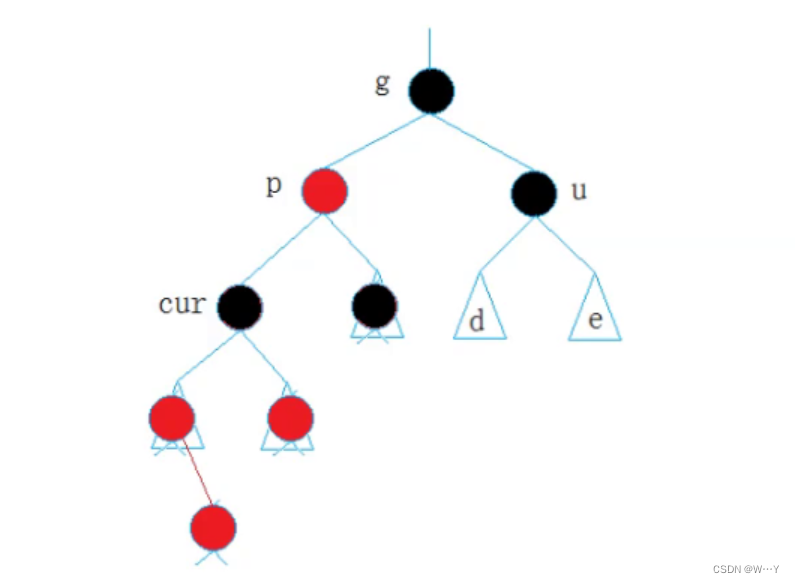
这时我们就无法用情况一的做法进行调整, 如果继续用情况一法则已经违反规则了。左右极度不均衡只能进行选择,这时我们就可以类比使用AVL树中的旋转法则。(旋转+变色)
p为g的左孩子,cur为p的左孩子,则进行右单旋转;相反,
p为g的右孩子,cur为p的右孩子,则进行左单旋转
p、g变色--p变黑,g变红
在变色时我们不区分其p与u节点的左右,但是在旋转时我们就要进行区分。
情况三: cur为红,p为红,g为黑,u不存在/u存在且为黑
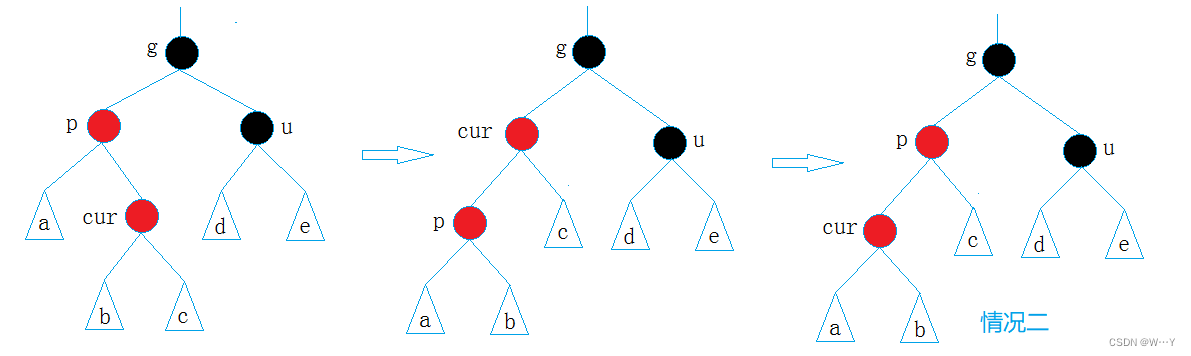
这种情况并不是一边高,而是两边都高左边高右边也高。所以我们得使用左右/右左双旋转。
p为g的左孩子,cur为p的右孩子,左右双旋+变色
p为g的右孩子,cur为p的左孩子,右左双旋+变色
针对每种情况进行相应的处理即可。
bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv); // 红色的if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;// 情况一:叔叔存在且为红if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续往上处理cur = grandfather;parent = cur->_parent;}else{// 情况二:叔叔不存在或者存在且为黑// 旋转+变色if (cur == parent->_left){// g// p u// cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// p u// cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;} }else{Node* uncle = grandfather->_left;// 情况一:叔叔存在且为红if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续往上处理cur = grandfather;parent = cur->_parent;}else{// 情况二:叔叔不存在或者存在且为黑// 旋转+变色// g// u p// cif (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// u p// cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}void RotateL(Node* parent){++rotateSize;Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;Node* ppnode = parent->_parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subR;}else{ppnode->_right = subR;}subR->_parent = ppnode;}}void RotateR(Node* parent){++rotateSize;Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;Node* ppnode = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subL;}else{ppnode->_right = subL;}subL->_parent = ppnode;}1.5 红黑树与AVL树的比较
红黑树和AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是O($log_2 N$),红黑树不追
求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对而言,降低了插入和旋转的次数,
所以在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单,所以实际运用中红
黑树更多。
2. 红黑树模拟实现STL中的map与set
我们模拟实现了红黑树,接下来就是对map与set的封装。
我们通过观察其stl源码切入进行仿写: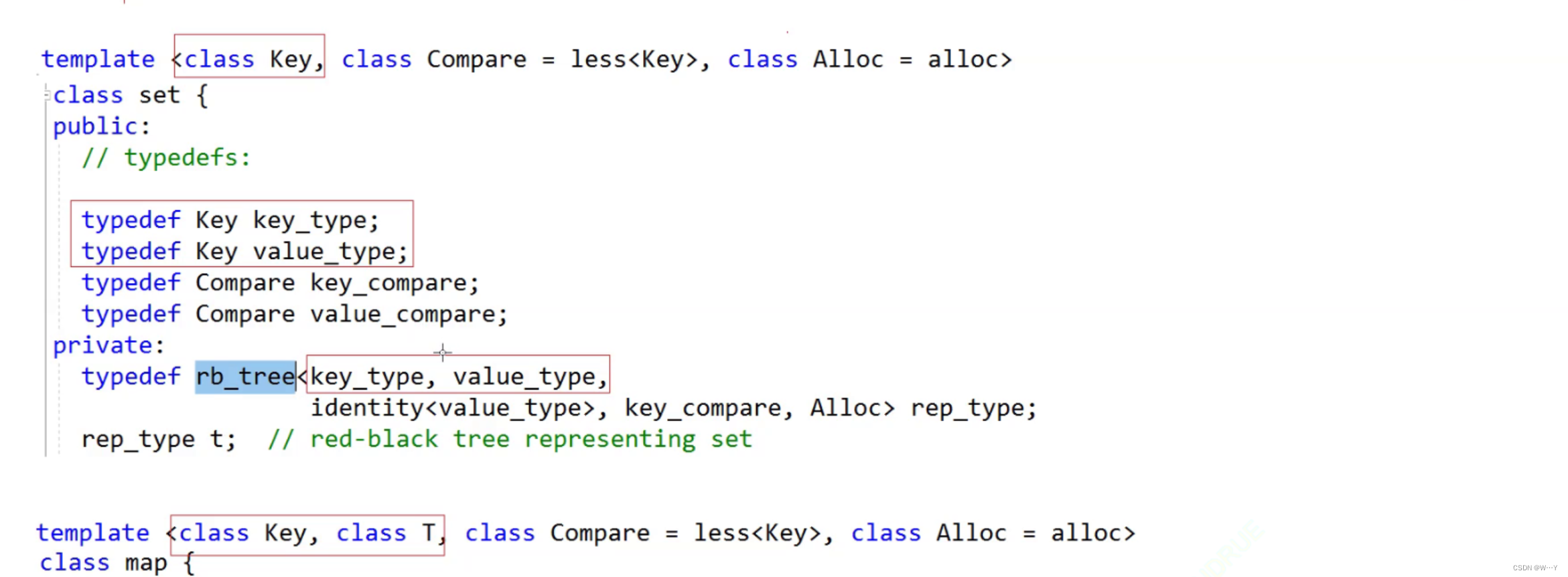
我们发现无论是map还是set都复用的一个红黑树,模板参数都是k,v模型。通过源码我们可以发现:set<k> -> rb_tree<k,k> map<k,v> ->rb_tree<k,pair<const k,v>>。所以节点中存什么内容是由v决定的,不是k决定的。将红黑树写成泛型,所以我们必须将上面写的红黑树的模板进行修改!

进行封装后就可以解决复用红黑树的模板。
但是使用红黑树的模板时,set和map所比较的对象不一样,因为set比较的就是key,而map比较的是value,所以我们就得使用仿函数进行操作,我们创建keyoft仿函数取出T对象中的key即可。
//set
struct SetKeyOfT{const K& operator()(const K& key){return key;}};//map
struct MapKeyOfT{const K& operator()(const pair<K, V>& kv){return kv.first;}};2.1 红黑树的迭代器
首先我们得封装一个红黑树的迭代器用来实现++、--、*、->、!=。这里的迭代器与list的迭代器非常类似,可以用一个指针来实现其内容。但是++与--必须确定下一个与上一个节点的关系,这里我们可以使用中序遍历解决,但是得用一个栈来辅助,这里我们不想使用这样的方法,我们可以找规律来实现:
++逻辑
1.it指向节点,右不为空,下一个就是右子树的最左节点
2.it指向节点,右为空,意味着这个节点的子树中序访问完了,下一个节点找祖先里面的孩子==父亲左的那个祖先。
--逻辑与++相反!
这样迭代器就很好解决了:
template<class T>
struct RBTreeIterator
{typedef RBTreeNode<T> Node;typedef RBTreeIterator<T> Self;Node* _node;RBTreeIterator(Node* node):_node(node){}T& operator*(){return _node->_data;}T* operator->(){return &_node->_data;}Self& operator++(){if (_node->_right){// 右子树的中序第一个(最左节点)Node* subLeft = _node->_right;while (subLeft->_left){subLeft = subLeft->_left;}_node = subLeft;}else{// 祖先里面孩子是父亲左的那个Node* cur = _node;Node* parent = cur->_parent;while (parent && cur == parent->_right){cur = parent;parent = cur->_parent;}_node = parent;}return *this;}Self& operator--(){// return *this;}bool operator!=(const Self& s){return _node != s._node;}bool operato == (const Self & s){return _node == s._node;}
};迭代器的好处是可以方便遍历,是数据结构的底层实现与用户透明。如果想要给红黑树增加迭代
器,需要考虑以前问题:
begin()与end()
STL明确规定,begin()与end()代表的是一段前闭后开的区间,而对红黑树进行中序遍历后,
可以得到一个有序的序列,因此:begin()可以放在红黑树中最小节点(即最左侧节点)的位
置,end()放在最大节点(最右侧节点)的下一个位置,关键是最大节点的下一个位置在哪块?
能否给成nullptr呢?答案是行不通的,因为对end()位置的迭代器进行--操作,必须要能找最
后一个元素,此处就不行,因此最好的方式是将end()放在头结点的位置:
typedef RBTreeIterator<T> iterator;iterator begin()
{Node* subLeft = _root;while (subLeft && subLeft->_left){subLeft = subLeft->_left;}return iterator(subLeft);
}iterator end()
{return iterator(nullptr);
}//map
typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::iterator iterator;
iterator begin()
{return _t.begin();
}iterator end()
{return _t.end();
}bool insert(const pair<K, V>& kv)
{return _t.Insert(kv);
}
//settypedef typename RBTree<K, const K, SetKeyOfT>::iterator iterator;iterator begin()
{return _t.begin();
}iterator end()
{return _t.end();
}bool insert(const K& key)
{return _t.Insert(key);
}
2.2 红黑树的改写与迭代器完整代码
#pragma once
#include<vector>enum Colour
{RED,BLACK
};template<class T>
struct RBTreeNode
{RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;Colour _col;T _data;RBTreeNode(const T& data):_left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _col(RED){}
};template<class T>
struct RBTreeIterator
{typedef RBTreeNode<T> Node;typedef RBTreeIterator<T> Self;Node* _node;RBTreeIterator(Node* node):_node(node){}T& operator*(){return _node->_data;}T* operator->(){return &_node->_data;}Self& operator++(){if (_node->_right){// 右子树的中序第一个(最左节点)Node* subLeft = _node->_right;while (subLeft->_left){subLeft = subLeft->_left;}_node = subLeft;}else{// 祖先里面孩子是父亲左的那个Node* cur = _node;Node* parent = cur->_parent;while (parent && cur == parent->_right){cur = parent;parent = cur->_parent;}_node = parent;}return *this;}Self& operator--(){// return *this;}bool operator!=(const Self& s){return _node != s._node;}bool operato == (const Self & s){return _node == s._node;}
};// set->RBTree<K, K, SetKeyOfT>
// map->RBTree<K, pair<K, V>, MapKeyOfT>// KeyOfT仿函数 取出T对象中的key
template<class K, class T, class KeyOfT>
class RBTree
{typedef RBTreeNode<T> Node;
public:typedef RBTreeIterator<T> iterator;iterator begin(){Node* subLeft = _root;while (subLeft && subLeft->_left){subLeft = subLeft->_left;}return iterator(subLeft);}iterator end(){return iterator(nullptr);}bool Insert(const T& data){if (_root == nullptr){_root = new Node(data);_root->_col = BLACK;return true;}KeyOfT kot;Node* parent = nullptr;Node* cur = _root;while (cur){if (kot(cur->_data) < kot(data)){parent = cur;cur = cur->_right;}else if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(data); // 红色的if (kot(parent->_data) < kot(data)){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;// 情况一:叔叔存在且为红if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续往上处理cur = grandfather;parent = cur->_parent;}else{// 情况二:叔叔不存在或者存在且为黑// 旋转+变色if (cur == parent->_left){// g// p u// cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// p u// cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else{Node* uncle = grandfather->_left;// 情况一:叔叔存在且为红if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续往上处理cur = grandfather;parent = cur->_parent;}else{// 情况二:叔叔不存在或者存在且为黑// 旋转+变色// g// u p// cif (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// u p// cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;Node* ppnode = parent->_parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subR;}else{ppnode->_right = subR;}subR->_parent = ppnode;}}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;Node* ppnode = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subL;}else{ppnode->_right = subL;}subL->_parent = ppnode;}}private:Node* _root = nullptr;
};2.3 map的封装
namespace why
{template<class K, class V>class map{struct MapKeyOfT{const K& operator()(const pair<K, V>& kv){return kv.first;}};public:typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::iterator iterator;iterator begin(){return _t.begin();}iterator end(){return _t.end();}bool insert(const pair<K, V>& kv){return _t.Insert(kv);}private:RBTree<K, pair<const K, V>, MapKeyOfT> _t;};
}2.4 set的封装
#include"RBTree.h"
namespace why
{template<class K>class set{struct SetKeyOfT{const K& operator()(const K& key){return key;}};public:typedef typename RBTree<K, const K, SetKeyOfT>::iterator iterator;iterator begin(){return _t.begin();}iterator end(){return _t.end();}bool insert(const K& key){return _t.Insert(key);}private:RBTree<K, const K, SetKeyOfT> _t;};
}
相关文章:

【C++历练之路】红黑树——map与set的封装实现
W...Y的个人主页💕 gitee代码仓库分享😊 前言:上篇博客中,我们为了使二叉搜索树不会出现”一边倒“的情况,使用了AVL树对搜索树进行了处理,从而解决了数据在有序或者接近有序时出现的情况。但是AVL树还会…...
RDB快照是怎么实现的?
RDB快照是怎么实现的? 前言快照怎么用?执行快照时,数据能被修改吗?RDB 和 AOF 合体 前言 虽说 Redis 是内存数据库,但是它为数据的持久化提供了两个技术。 分别是「 AOF 日志和 RDB 快照」。 这两种技术都会用各用一…...
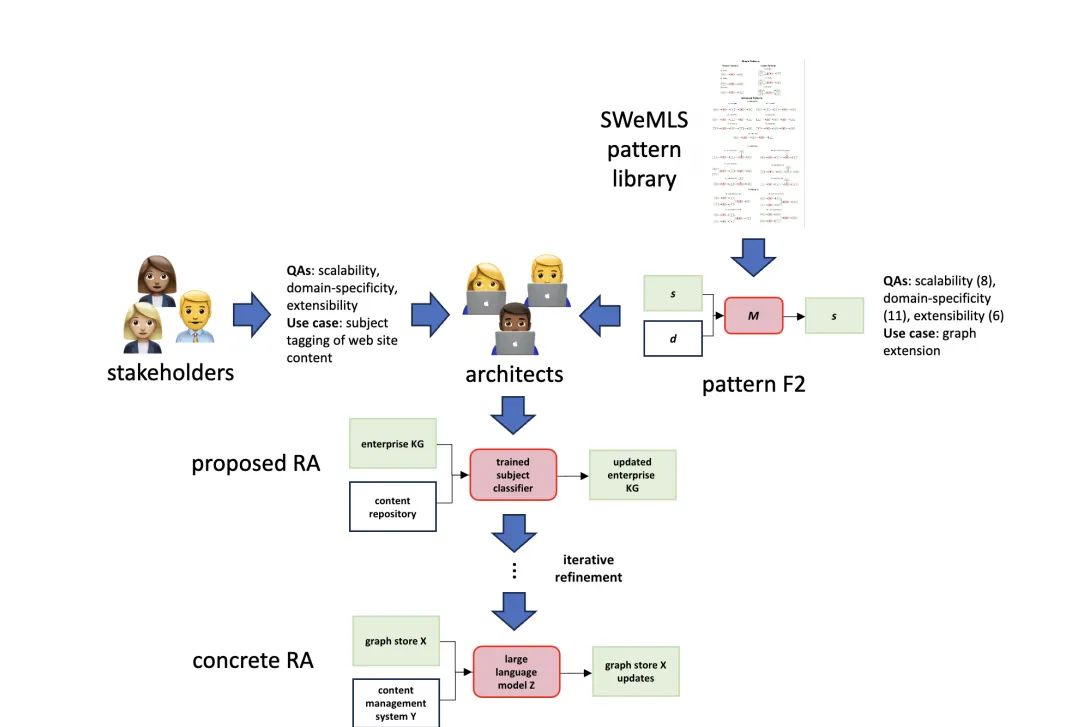
智能体可靠性的革命性提升,揭秘知识工程领域的参考架构新篇章
引言:知识工程的演变与重要性 知识工程(Knowledge Engineering,KE)是一个涉及激发、捕获、概念化和形式化知识以用于信息系统的过程。自计算机科学和人工智能(AI)历史以来,知识工程的工作流程因…...

Shell 初始化配置指北 | Ubuntu
唠唠闲话 概要:在不同的Shell环境(如Bash和Zsh)中设置环境变量、设置初始脚本,以及如何根据不同的使用场景(用户级或系统级)管理和设置初始运行命令。 p.s. 如果你很熟悉 Linux,推荐跳到最后一…...
[嵌入式系统-69]:RT-Thread-组件:网络组件“组”,RT-Thread系统通向外部网络世界的入口
目录 RT-Thread 提供的网络世界入口 - 网络组件 1. 总概 2. AT 3. Lwip: 轻量级IP协议栈 4. W5500 5. Netdev 6. RT-Thread SAL(Socket Abstraction Layer)套接字和BSD套接字区别 RT-Thread SAL 套接字接口示例 BSD 套接字接口示例 …...

Linux学习笔记1---Windows上运行Linux
在正点原子的教程中学习linux需要安装虚拟机或者在电脑上安装一个Ubuntu系统,但个人觉得太麻烦了,现在linux之父加入了微软,因此在Windows上也可以运行linux 了。具体方法如下: 一、 在Windows上的设置 在window的搜索框内&#…...

Java算法-力扣leetcode-135. 分发糖果
135. 分发糖果 n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。 你需要按照以下要求,给这些孩子分发糖果: 每个孩子至少分配到 1 个糖果。相邻两个孩子评分更高的孩子会获得更多的糖果。 请你给每个孩子分发糖果,计算并…...
企业为什么需要主数据管理工具?十大热门主数据管理工具盘点
主数据管理是一套综合性的策略和技术,用于协调和管理企业内用于识别关键业务实体(如客户、产品、供应商和员工)的一致性、准确性和统一性的数据。主数据管理的目的是创建一个“单一真相源”,确保在不同部门和系统之间共享的数据保…...

免费思维13招之一:体验型思维
思维01:体验型思维 第一大战略:体验型思维。 体验型思维是免费思维中最简单的思维,我们先从最简单的讲起,由简入繁,简单的我们少讲,复杂的我们多讲。 那么,什么是体验型思维呢? 很简单,就是先让客户进行体验,再进行成交的方式。这一种思维,具体的可以分为两种:…...

面试C++(基础篇)-NULL与nullptr的区别?
3: NULL与nullptr的区别? 在C中,NULL和nullptr都用于表示空指针,但它们之间存在一些关键的区别: 1. 来源和含义: • NULL:在C中,NULL最初是从C语言中继承过来的,定义在<cstddef…...

「AIGC」深度学习
深度学习是机器学习的一个子领域,它基于人工神经网络的学习算法。深度学习在图像和语音识别、自然语言处理、医学图像分析、药物发现、自动驾驶汽车等领域取得了显著的进展。以下是围绕深度学习的几个关键主题的阐述。 学习路线 基础数学: 了解线性代数…...
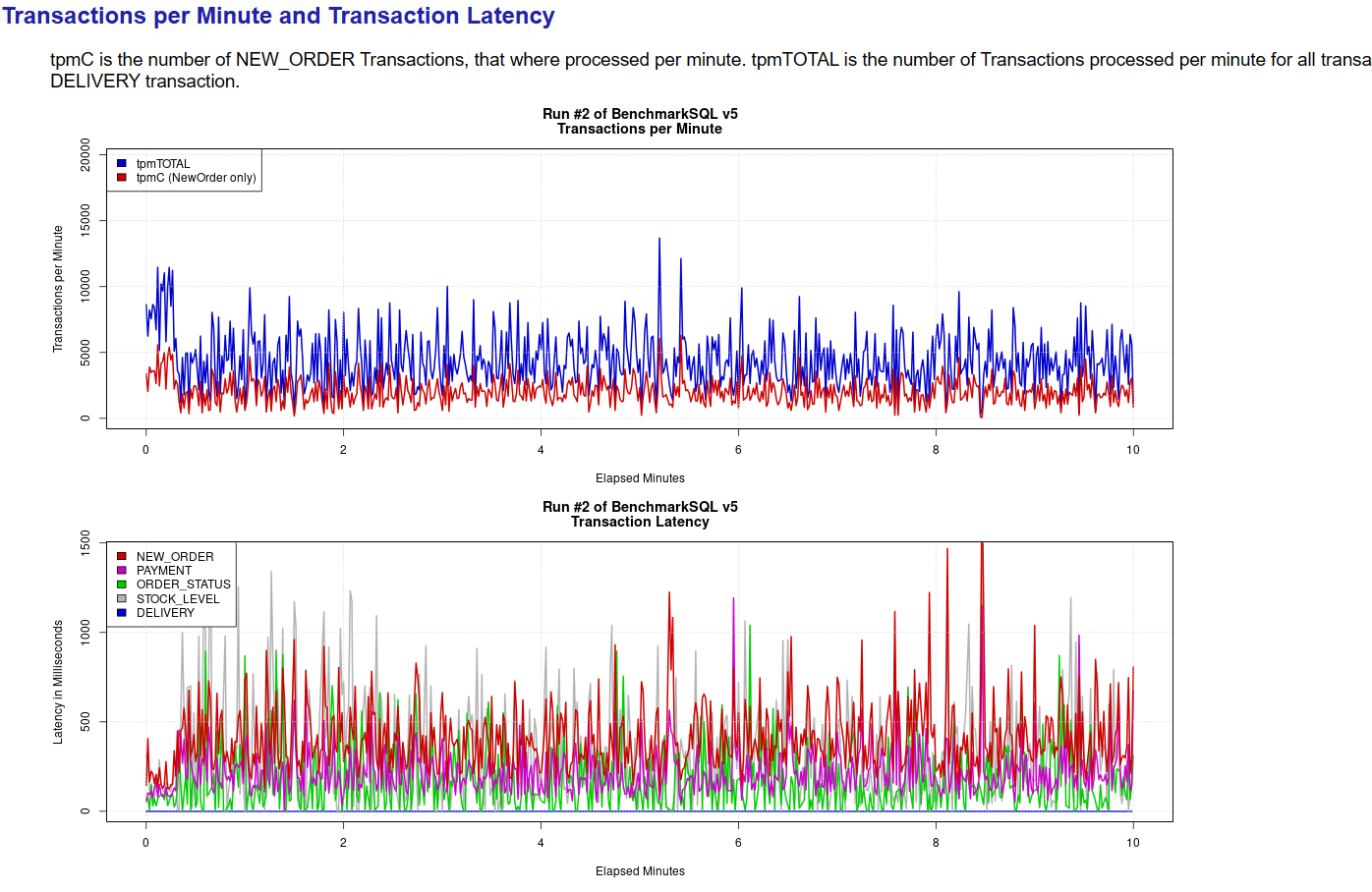
mysql5.7数据库安装及性能测试
mysql5.7数据库安装及性能测试 记录Centos7.9下安装mysql 5.7并利用benchmark工具简单测试mysql的性能。 测试机:centos7.9 配置:4C8G40G 1. 下安装mysql5.7 安装mysql5.7: # 通过官方镜像源安装$ wget http://dev.mysql.com/get/mysql57-com…...

聪明与诚实:社会信任的桥梁
在现代社会中,我们经常听到这样的评价:“某人真聪明。”然而,当我们深入思考时,会发现“聪明”这个词背后所承载的含义并不单一。聪明和狡诈往往被混淆,而诚实的价值却时常被忽视。在一个高度诚信的社会里,…...

基于单片机的无线数据传输系统设计
摘要:基于单片机的无线数据传输系统的设计,实现了温度和湿度的自动采集、无线通讯和报警功能。该系统包括了LCD1602显示电路、DHT11温湿度采集电路等,完成了基于无线数据传输的方法来实现温湿度的采集。 关键词:温湿度检测;N RF 24 L 01;单片机 0 引言 随着科技水平的提高,…...

【IP:Internet Protocol,子网(Subnets),IPv6:动机,层次编址:路由聚集(rout aggregation)】
文章目录 IP:Internet Protocol互联网的的网络层IP分片和重组(Fragmentation & Reassembly)IP编址:引论子网(Subnets)特殊IP地址IP 编址: CIDR子网掩码(Subnet mask)转发表和转发…...

智启算力平台基本操作
智启算力平台 智启算力平台路径搭载数据集搭载镜像配置 智启算力平台 开发文档 帮助文档 - OpenI - 启智AI开源社区 路径搭载 OpenIOSSG/promote: 启智AI协作平台首页推荐组织及推荐项目申请。 - notice/Other_notes/SDKGetPath.md at master - promote - OpenI - 启智AI开…...

微信小程序 【关键部分】
1. 动机 最近在开发小程序,小程序既需兼顾针对新用户的内容预览,又要为注册用户提供服务,简单梳理下,基本需求如下: 小程序共三个tab页,所有用户都可以浏览首页内容,了解我们可以提供的优质服…...

JavaEE技术之MySql高级(索引、索引优化、sql实战、View视图、Mysql日志和锁、多版本并发控制)
文章目录 1. MySQL简介2. MySQL安装2.1 MySQL8新特性2.2 安装MySQL2.2.1 在docker中创建并启动MySQL容器:2.2.2 修改mysql密码2.2.3 重启mysql容器2.2.4 常见问题解决 2.3 字符集问题2.4 远程访问MySQL(用户与权限管理)2.4.0 远程连接问题1、防火墙2、账号不支持远程…...
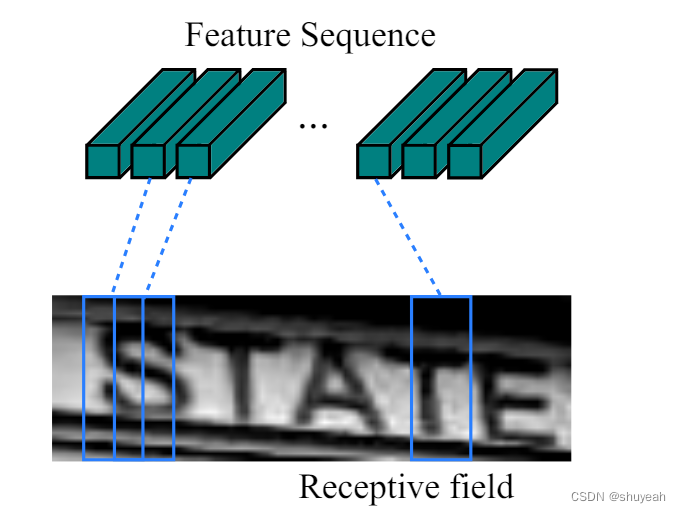
OCR文本识别模型CRNN
CRNN网络结构 论文地址:https://arxiv.org/pdf/1507.05717 参考:https://blog.csdn.net/xiaosongshine/article/details/112198145 git:https://github.com/shuyeah2356/crnn.pytorch CRNN文本识别实现端到端的不定长文本识别。 CRNN网络把包含三部分&…...

【数据结构】闲谈A股实时交易的数据结构-队列
今天有点忙,特意早起,要不先写点什么。看到个股的红红绿绿, 突然兴起,要不写篇文章分析下A股交易的简易版数据结构。 在A股实时股票交易系统中,按照个人理解,大致会用队列来完成整个交易。队列(…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...
