RPC 失败。curl 16 Error in the HTTP2 framing layer
报错：
(base) h@h-virtual-machine:~/work$ git clone https://github.com/yangzongzhuan/RuoYi-Vue3.git
正克隆到 'RuoYi-Vue3'...
error: RPC 失败。curl 16 Error in the HTTP2 framing layer
fatal: 在引用列表之后应该有一个 flush 包
这个错误通常是由于 Git 在网络传输时遇到了问题导致的。一种可能的解决方法是使用 git clone 命令的 --depth 参数，限制克隆的深度，以减少网络传输中的数据量。你可以尝试使用如下命令：
git clone --depth=1 https://github.com/yangzongzhuan/RuoYi-Vue3.git
这会将克隆的历史记录限制为最近的一次提交，从而减少传输数据量。
相关文章：
RPC 失败。curl 16 Error in the HTTP2 framing layer
报错： (base) hh-virtual-machine:~/work$ git clone https://github.com/yangzongzhuan/RuoYi-Vue3.git 正克隆到 RuoYi-Vue3... error: RPC 失败。curl 16 Error in the HTTP2 framing layer fatal: 在引用列表之后应该有一个 flush 包这个错误通常是由于 Git 在…...
（图论）最短路问题合集（包含C,C++,Java,Python,Go）
不存在负权边： 1.朴素dijkstra算法 原题： 思路：（依然是贪心的思想） 1.初始化距离：dis[1]0，dis[i]INF（正无穷） 2.循环n次： 找到当前不在s中的dis最小的点&…...
电脑文件批量重命名不求人：快速操作，高效技巧让你轻松搞定
在数字化时代，电脑文件的管理与整理显得尤为重要。当面对大量需要重命名的文件时，一个个手动修改不仅耗时，还容易出错。那么，有没有一种方法可以快速、高效地完成这一任务呢？答案是肯定的，下面就来介绍几种…...
基于springboot的网上点餐系统源码数据库
基于springboot的网上点餐系统源码数据库 随着科学技术的飞速发展，各行各业都在努力与现代先进技术接轨，通过科技手段提高自身的优势；对于网上点餐系统当然也不能排除在外，随着网络技术的不断成熟，带动了网上点餐系统…...
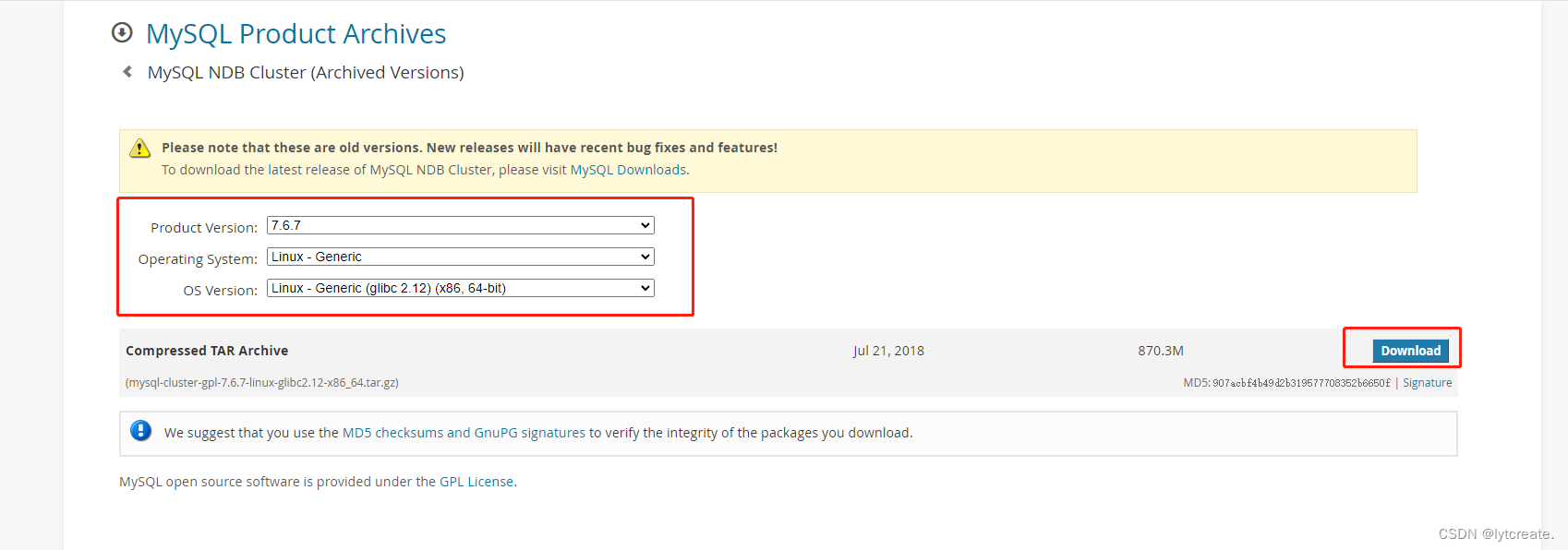
mysql cluster数据库集群介绍、部署及配置
前言： MySQL集群是一个无共享的、分布式节点架构的存储方案，旨在提供容错性和高性能。它由三个主要节点组成：管理节点（MGM）、数据节点和SQL节点。 管理节点（MGM） 定义与用途：管理节点是MySQL Cluster的控制中心，负责管理集群内的其他节点。它提供配置数据，启动和停止…...
uniapp的app端软件更新弹框
1：使用html PLUS实现：地址HTML5 API Reference (html5plus.org)，效果图 2：在app.vue的onLaunch生命周期中，代码如下： onLaunch: function() {let a 0let view new plus.nativeObj.View(maskView, {backg…...
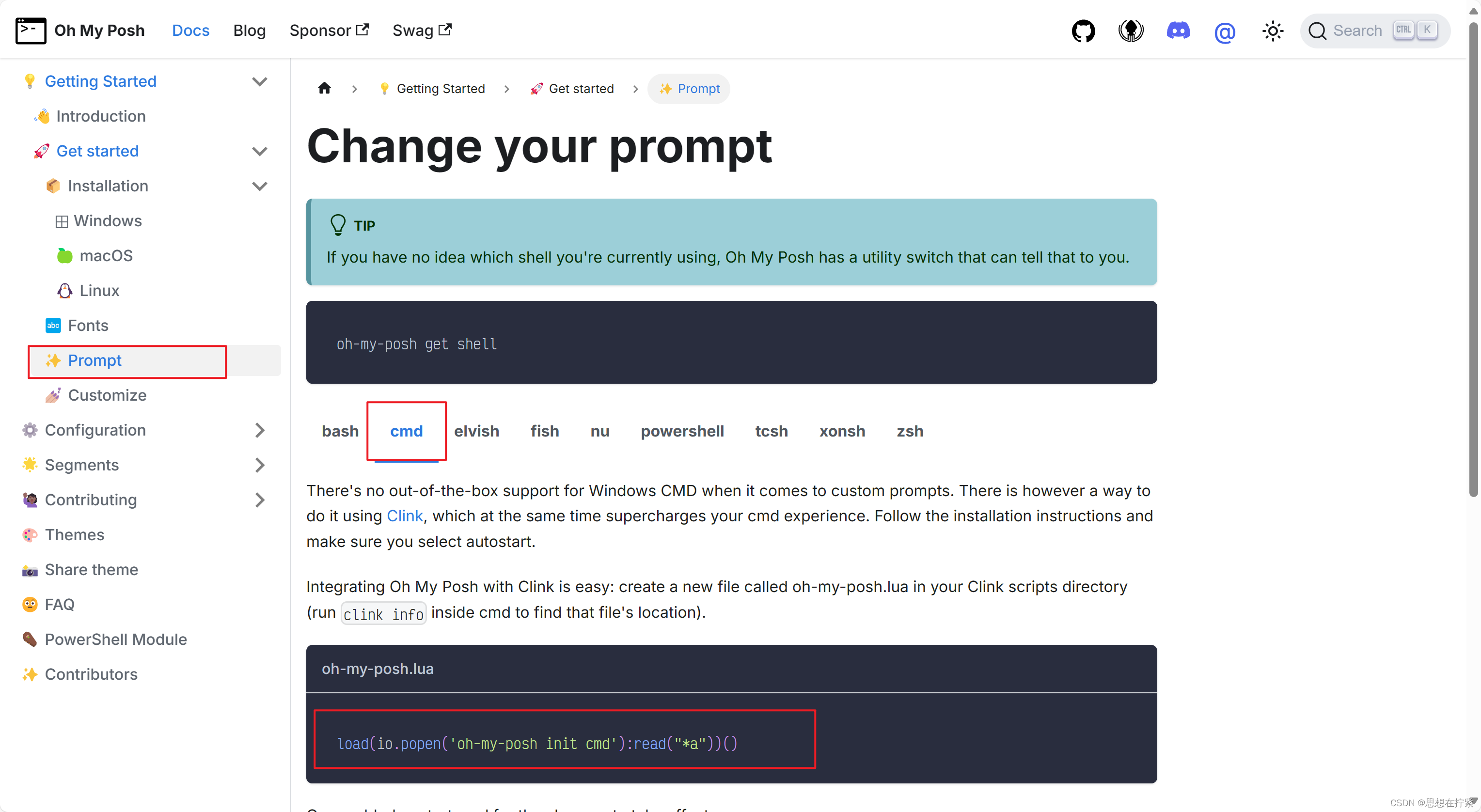
win11 Terminal 部分窗口美化
需求及分析：因为在 cmd、anaconda prompt 窗口中输入命令较多，而命令输入行和输出结果都是同一个颜色，不易阅读，故将需求定性为「美化窗口」。 美化结束后，我在想是否能不安装任何软件，简单地通过调整主题颜…...
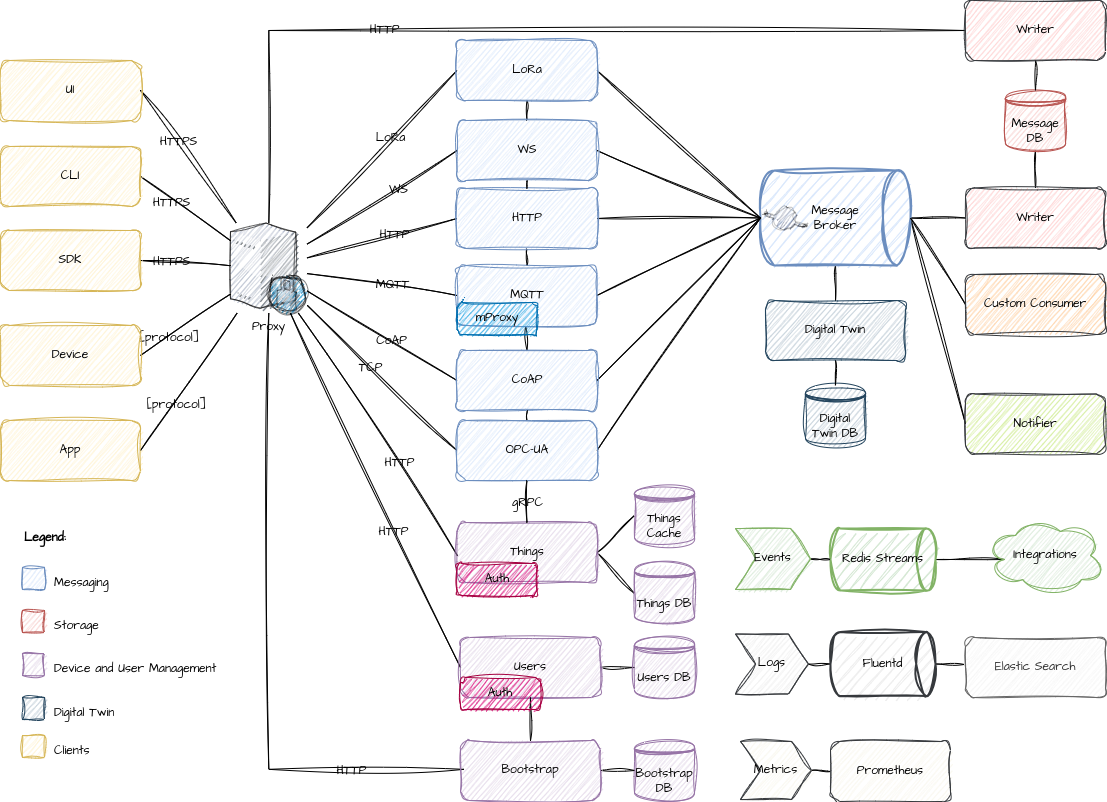
开源go实现的iot物联网新基建平台
软件介绍 Magistrala IoT平台是由Abstract Machines公司开发的创新基础设施解决方案，旨在帮助组织和开发者构建安全、可扩展和创新的物联网应用程序。曾经被称为Mainflux的平台，现在已经开源，并在国际物联网领域受到广泛关注。 功能描述 多协…...
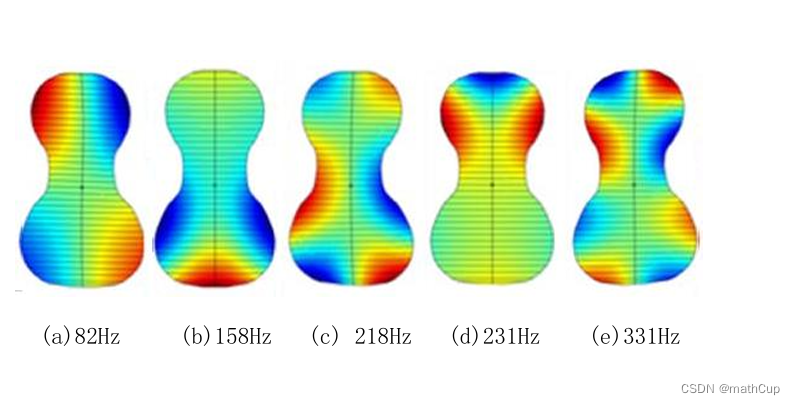
24深圳杯ABCD成品论文47页＋各小问代码＋图表
A题多个火箭残骸的准确定位： A题已经更新完22页完整版论文＋高清无水印照片＋Python（MATLAB）代码简单麦麦https://www.jdmm.cc/file/2710544/ 问题1：单个残骸的音爆位置确定 建模思路： 1. 声波传…...
doris经典bug
在部署完登录web页面查看的时候会发现只有一个节点可以读取信息剩余的节点什么也没读取到 在发现问题后，我们去对应的节点去看log日志，发现它自己绑定到前端的地址上了 现在我们已经发现问题了，以下就开始解决问题 重置doris 首先对be进行操…...
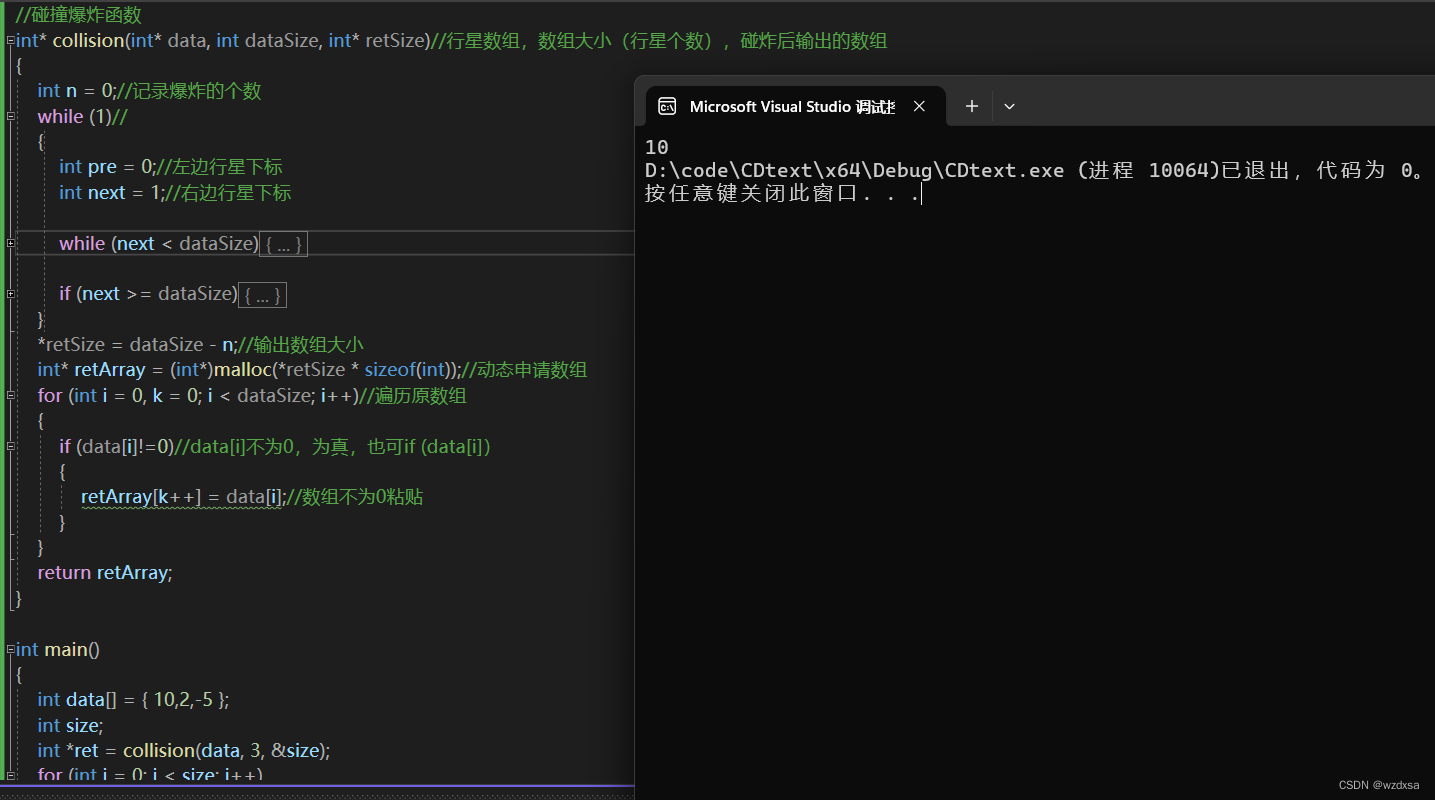
贪心算法应用例题
最优装载问题 #include <stdio.h> #include <algorithm>//排序int main() {int data[] { 8,20,5,80,3,420,14,330,70 };//物体重量int max 500;//船容最大总重量int count sizeof(data) / sizeof(data[0]);//物体数量std::sort(data, data count);//排序,排完数…...
亚信科技精彩亮相2024中国移动算力网络大会，数智创新共筑“新质生产力”
4月28至29日，江苏省人民政府指导、中国移动通信集团有限公司主办的2024中国移动算力网络大会在苏州举办。大会以“算力网络点亮AI时代”为主题，旨在凝聚生态伙伴合力，共同探索算力网络、云计算等数智能力空间，共促我国算网产业和数…...
图像处理中的颜色空间转换
在图像处理中，颜色空间转换是指将图像从一种颜色表示方式转换为另一种颜色表示方式。常见的颜色空间转换包括RGB到HSV、RGB到灰度、RGB到CMYK等。 RGB到HSV转换： RGB颜色空间由红色（R）、绿色（G）和蓝色&…...
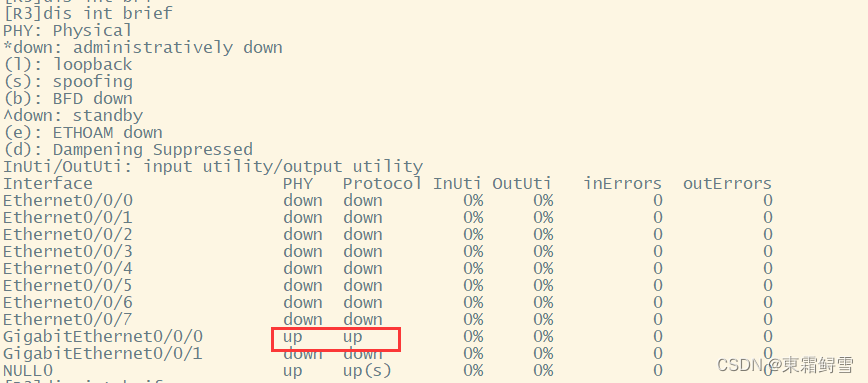
网络安全之静态路由
以下是一个静态路由的拓扑图 Aping通B，C可以ping通D。 路由器转发数据需要路由表，但仍可以Aping通B，C可以ping通D，是因为产生了直连路由：产生的条件有两个，接口有IP，接口双up(物理upÿ…...
Golang | Leetcode Golang题解之第74题搜索二维矩阵
题目： 题解： func searchMatrix(matrix [][]int, target int) bool {m, n : len(matrix), len(matrix[0])i : sort.Search(m*n, func(i int) bool { return matrix[i/n][i%n] > target })return i < m*n && matrix[i/n][i%n] target }...
2023黑马头条.微服务项目.跟学笔记(五)
2023黑马头条.微服务项目.跟学笔记 五 延迟任务精准发布文章 1.文章定时发布2.延迟任务概述 2.1 什么是延迟任务2.2 技术对比 2.2.1 DelayQueue2.2.2 RabbitMQ实现延迟任务2.2.3 redis实现3.redis实现延迟任务4.延迟任务服务实现 4.1 搭建heima-leadnews-schedule模块4.2 数据库…...
C语言 | Leetcode C语言题解之第75题颜色分类
题目： 题解： void swap(int *a, int *b) {int t *a;*a *b, *b t; }void sortColors(int *nums, int numsSize) {int p0 0, p2 numsSize - 1;for (int i 0; i < p2; i) {while (i < p2 && nums[i] 2) {swap(&nums[i], &num…...
淘宝扭蛋机小程序开发：掌上惊喜，转出你的幸运宝藏
一、全新玩法，尽在掌中 淘宝扭蛋机小程序，将传统的扭蛋乐趣与数字时代完美结合，为您带来全新的购物体验。在这个小小的平台上，您可以用手指轻松操控，探索无尽的宝藏世界，转出专属于您的幸运好物。 二、海…...
Oracle索引组织表与大对象平滑迁移至OceanBase的实施方案
作者简介：严军(花名吉远)，十年以上专注于数据库存储领域，精通Oracle、Mysql、OceanBase，对大数据、分布式、高并发、高性能、高可用有丰富的经验。主导过蚂蚁集团核心系统数据库升级，数据库LDC单元化多活项目ÿ…...
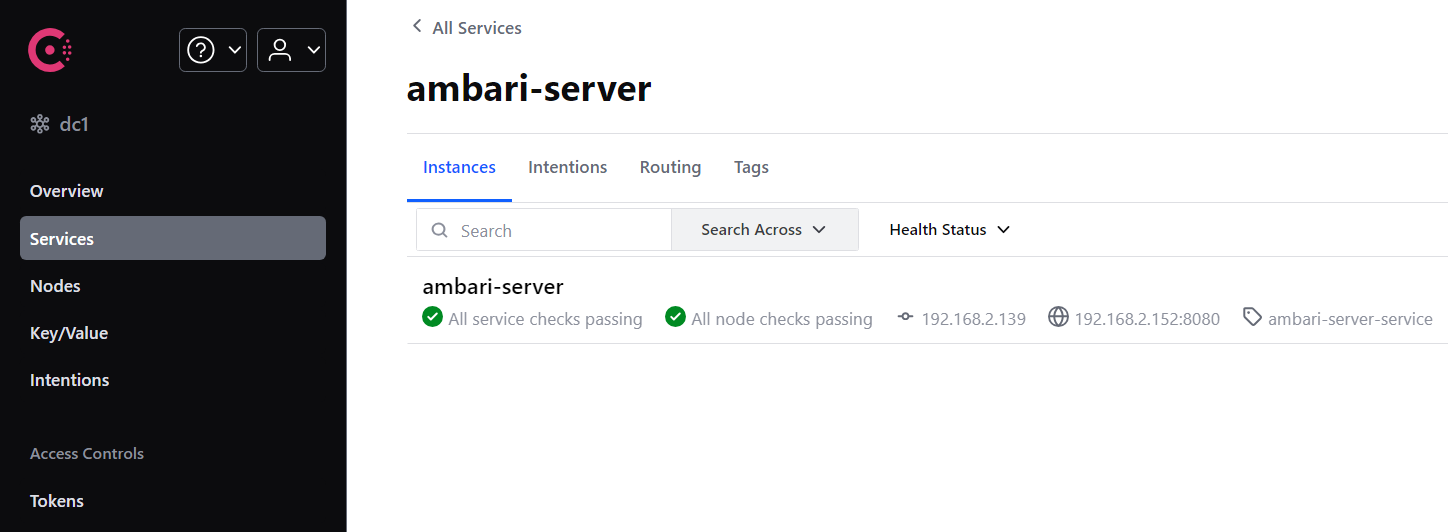
【服务治理中间件】consul介绍和基本原理
目录 一、CAP定理 二、服务注册中心产品比较 三、Consul概述 3.1 什么是Consul 3.2 Consul架构 3.3 Consul的使用场景 3.4 Consul健康检查 四、部署consul集群 4.1 服务器部署规划 4.2 下载解压 4.3 启动consul 五、服务注册到consul 一、CAP定理 CAP定理ÿ…...
css实现圆环展示百分比，根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...
ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上，你可以使用apt包管理器来安装NFS服务器。打开终端并运行： sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享，例如/shared： sudo mkdir /shared sud…...
VB.net复制Ntag213卡写入UID
本示例使用的发卡器：https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...
微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注：文档 https://developers.weixin.qq…...
是否存在路径（FIFOBB算法）
题目描述 一个具有 n 个顶点e条边的无向图，该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序，确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数，分别表示n 和 e 的值（1…...
OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波（Mean Shift Filtering）函数meanShiftFiltering()
操作系统：ubuntu22.04 OpenCV版本：OpenCV4.9 IDE:Visual Studio Code 编程语言：C11 算法描述 在 GPU 上对图像执行 均值漂移滤波（Mean Shift Filtering），用于图像分割或平滑处理。 该函数将输入图像中的…...
有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机（Finite Automaton, FA）到正规文法（Regular Grammar）转换器，它配备了一个直观且完整的图形用户界面，使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...
React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store： 我们在使用异步的时候理应是要使用中间件的，但是configureStore 已经自动集成了 redux-thunk，注意action里面要返回函数 import { configureS…...
深度学习水论文：mamba＋图像增强
🧀当前视觉领域对高效长序列建模需求激增，对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模，以及动态计算优势，在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内，就有不…...
机器学习的数学基础：线性模型
线性模型 线性模型的基本形式为： f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法，得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...