损失函数详解
1.损失函数
是一种衡量模型与数据吻合程度的算法。损失函数测量实际测量值和预测值之间差距的一种方式。损失函数的值越高预测就越错误,损失函数值越低则预测越接近真实值。对每个单独的观测(数据点)计算损失函数。将所有损失函数(loss function)的值取平均值的函数称为代价函数(cost function),更简单的理解就是损失函数是针对单个样本的,而代价函数是针对所有样本的。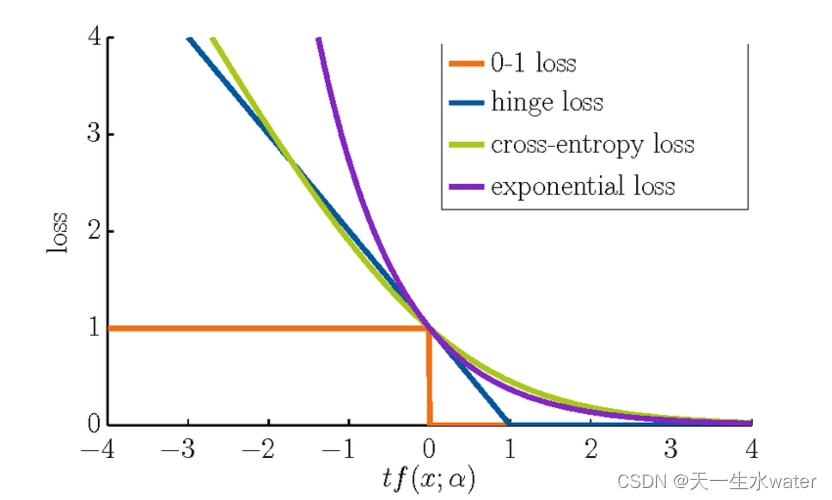
2.为什么要用损失函数?
由于损失函数测量的是预测值和实际值之间的差距,因此在训练模型时可以使用它们来指导模型的改进(通常的梯度下降法)。在构建模型的过程中,如果特征的权重发生了变化得到了更好或更差的预测,就需要利用损失函数来判断模型中特征的权重是否需要改变,以及改变的方向。
损失函数有很多种,主要可以分为以下几类:
-
均方误差损失函数(Mean Squared Error, MSE):
- 应用场景:通常用于回归问题。
- 表达式:
- 其中
是真实值,
是预测值,
是样本数量。
-
交叉熵损失函数(Cross-Entropy Loss):
- 应用场景:常用于分类问题。
- 二分类交叉熵表达式:
- 多分类交叉熵表达式:
- 其中
是第
个样本属于类别
的真实标记,
是预测概率。
- 交叉熵损失函数(Cross-Entropy Loss Function)-CSDN博客
-
绝对误差损失函数(Mean Absolute Error, MAE):
- 应用场景:回归问题。
- 表达式:
-
Hinge损失函数:
- 应用场景:用于支持向量机(SVM)中的二分类问题。
- 表达式:
- 其中
是实际类标签(+1 或 -1),
是预测值。
-
对数损失函数(Log Loss):
- 应用场景:二分类和多分类问题的一种变体,与交叉熵类似。
3.不同的损失函数对神经网络的训练有不同的影响
为了更好地理解不同的损失函数如何影响神经网络的训练结果,以下通过图像生成领域的一个具体示例进行说明:图像超分辨率任务。
问题背景
图像超分辨率任务是指通过输入低分辨率图像生成对应的高分辨率图像。训练神经网络模型以生成高质量的高分辨率图像时,不同的损失函数将对最终结果产生不同的影响。
使用的损失函数类型
- 均方误差损失(MSE Loss)
- 感知损失(Perceptual Loss)
- 对抗损失(Adversarial Loss)
- 结构相似度损失(SSIM Loss)
示例任务:超分辨率任务中的不同损失函数影响
- 输入数据:一组低分辨率图像(如
- 目标输出:对应的高分辨率图像(如
)。
- 模型架构:简单的卷积神经网络(CNN)。
不同损失函数对训练的影响
-
均方误差损失(MSE Loss)
- 定义:计算输出图像和目标图像像素之间的均方误差。
- 公式:
优点:简单,易于计算。
缺点:忽略了人类视觉系统对图像纹理和细节的敏感性,生成的图像通常看起来模糊。 -
感知损失(Perceptual Loss)
- 定义:通过比较输出图像和目标图像在预训练的卷积神经网络中的某些中间层的特征来计算差异。
- 优点:生成的图像在视觉上更贴近目标图像。
- 缺点:计算复杂度相对较高。
-
对抗损失(Adversarial Loss)
- 定义:通过一个附加的判别器网络,鼓励生成的图像在视觉上无法与真实图像区分。
- 优点:生成的图像在细节上更加锐利和真实。
- 缺点:可能产生伪影(Artifacts),且训练不稳定。
-
结构相似度损失(SSIM Loss)
- 定义:基于亮度、对比度和结构等方面计算输出图像与目标图像之间的结构相似性。
- 优点:在视觉感知方面更符合人类认知,生成图像的对比度和纹理效果更佳。
- 缺点:可能无法精确捕获到非常细微的像素差异。
实验结果对比
实验设置:使用相同的数据集和模型架构,仅改变损失函数,比较不同损失函数对超分辨率任务生成效果的影响。
-
MSE Loss
- 结果:生成的高分辨率图像相对较模糊,但整体结构准确。
- PSNR(峰值信噪比):30.5 dB
-
Perceptual Loss
- 结果:生成的图像更加锐利且纹理更清晰。
- PSNR:29.1 dB
-
Adversarial Loss
- 结果:生成的图像在细节上更锐利,但可能存在伪影。
- PSNR:28.7 dB
-
SSIM Loss
- 结果:生成的图像在结构相似性上更符合目标图像,但在细节上不如感知损失和对抗损失。
- PSNR:29.8 dB
通过以上示例,可以看出不同的损失函数在图像生成任务中产生了不同的效果。具体而言:
- MSE Loss 适用于追求整体结构的准确性,但会导致图像模糊。
- Perceptual Loss 在视觉上更符合人类的感知,更加锐利,但PSNR较低。
- Adversarial Loss 在细节上更锐利,但需要额外的判别器网络,可能引入伪影。
- SSIM Loss 综合了结构相似性和细节效果,但可能不如其他高级损失函数。
因此,选择损失函数应基于具体应用的目标和需求来定。
4.如何设计损失函数:
设计损失函数时,应考虑以下关键因素:
损失函数的设计是机器学习和深度学习中的一个核心环节,它需要根据具体任务、数据特性和预期目标进行精细化设计。通过持续的实验和优化,可以显著提高模型的性能和适应性。
-
问题类型
- 回归问题:通常使用均方误差(MSE)、平均绝对误差(MAE)等连续值误差度量。
- 分类问题:使用交叉熵损失(Cross-Entropy Loss)等概率误差度量,如多分类交叉熵损失或二元交叉熵损失。
- 结构化输出问题:使用特定于任务的损失,例如在序列生成或图像分割中可能使用逐像素交叉熵损失或序列损失。
-
优化难易度
- 损失函数需要兼顾易于优化的性质,如避免过多的局部最小值或梯度消失问题。设计时,可以选择平滑且连续的函数形式。
-
任务特定需求
- 根据任务的特定需求设计损失函数。例如,在图像增强中可能会优先考虑结构相似性或感知相似性;在对抗性任务中,可能需要设计能够处理生成器和判别器间竞争的对抗性损失。
-
可解释性和合理性
- 设计的损失函数应当具备直观的解释性,使模型的行为与优化目标相符,且易于理解和解释。
-
实践中的设计技巧
- 损失函数的组合:通常将多个损失函数组合使用,如结合基本损失和正则化项(例如L1正则、L2正则)来提升模型的泛化能力。
- 感知驱动的设计:在图像处理和语音识别等领域,可以引入基于人类感知特征的损失函数,使模型输出更符合人类的感知习惯。
- 实验和调整:设计损失函数时,经常需要通过实验来调整和比较不同损失函数的表现,以找到最适合当前任务的函数形式。
4.1在回归问题中计损失函数
我们需要考虑到数据的特性、目标的特点以及模型的健壮性。以下是一个具体的例子,我们将设计一个损失函数来处理潜在的异常值问题,并确保模型能够对大部分数据进行良好的预测。
问题描述
假设我们有一个房价预测问题,其中目标是预测不同地区的房屋售价。房价数据经常会受到异常值的影响,比如极其昂贵或极其便宜的房产。这种情况下,传统的均方误差(MSE)损失函数可能会因为对异常值过于敏感而不是最佳选择。
损失函数设计
为了减少异常值的影响,我们可以设计一个损失函数,结合了均方误差(MSE)和平均绝对误差(MAE),这种组合可以平衡对异常值的敏感度和损失函数的稳定性。
损失函数表达式
我们可以定义一个混合损失函数,如下: 其中,
是一个介于0和1之间的参数,用于调控MSE和MAE的贡献比重。
-
MSE (均方误差):
-
MAE (平均绝对误差):
参数选择
可以开始作为一个基线,这样MSE和MAE各占一半权重。根据模型在验证数据上的表现,我们可以调整 (\alpha) 的值:
- 如果模型对异常值过于敏感,可以减小
,增加MAE的权重。
- 如果模型需要更精确地拟合数据(即使是一些异常值),可以增加
,增加MSE的权重。
- 如果模型对异常值过于敏感,可以减小
实验与调整
通过实验和调整,我们可以找到最适合当前数据和任务的 值。通常,这涉及到在交叉验证过程中观察不同 (\alpha) 值的效果,选择在验证集上表现最好的设置。
通过设计一个混合型损失函数,我们可以有效地处理含有异常值的回归问题,使模型在保持健壮性的同时也能准确预测大部分数据。这种方法提供了灵活性和适应性,适用于各种不同的回归任务和数据集。
4.2在分类问题中设计损失函数
因为它直接影响到模型的优化方向和最终性能。让我们通过一个多分类问题的例子来说明如何设计损失函数,这里我们考虑的是一个典型的图像分类问题,如识别不同类型的动物。
问题描述
假设我们有一个图像数据集,包含了多种动物,如猫、狗、鸟等。我们的任务是开发一个模型,能够正确分类每一张图片中的动物类型。
损失函数设计
对于多分类问题,常用的损失函数是交叉熵损失(Cross-Entropy Loss),它非常适合处理类别之间互斥的情况(即一张图片只能标记为一个类别)。
交叉熵损失函数
交叉熵损失函数度量的是实际输出概率分布和预测输出概率分布之间的差异。其数学表达式为: 其中:
是类别的数量,
是一个布尔值,表示类别
是否是正确的分类标签,
是模型预测图片属于类别
的概率。
选择和优化
-
权重: 在类别不平衡的情况下,例如某些类别的样本远多于其他类别,可以为交叉熵损失引入类别权重,使得模型更加关注少数类:
其中,
是类别
的权重,通常与类别频率成反比。
-
标签平滑:为了增强模型的泛化能力,防止模型过于自信,可以使用标签平滑技术(Label Smoothing)。这种方法将真实标签的一部分置信度分配给其他错误标签,从而软化真实标签:
其中
是一个小的常数(如0.1),这样每个类别都会得到一小部分置信度。
实验与调整
- 通过在验证集上评估模型性能,调整类别权重和标签平滑参数。
- 观察混淆矩阵,了解模型在哪些类别上表现不佳,可能需要调整特定类别的权重或收集更多数据。
在多分类问题中,交叉熵损失是一个强大的工具,特别是结合类别权重和标签平滑技术,可以显著提高模型对不平衡数据的分类精度和泛化能力。通过不断试验和优化,我们可以为具体问题找到最适合的损失函数配置。
5图像应用中常见的损失函数
5.1图像分割任务
图像分割的目标是将图像中的每个像素分配到一个特定的类别(如对象、背景等)。这一任务可以看作是逐像素的分类问题,因此常用的损失函数在本质上与分类任务相似,但也有专门针对分割特性的优化和变体。
常见的图像分割损失函数
-
交叉熵损失(Cross-Entropy Loss)
- 就像在普通的分类任务中一样,交叉熵损失也可以用于图像分割。它逐像素计算预测分类的概率和实际分类的匹配程度。
- 对于多类分割问题,通常使用多类交叉熵损失。
-
Dice Loss
- Dice Loss基于Dice系数,后者是一种衡量两个样本相似度的统计工具,特别适用于样本大小不平衡的情况。Dice Loss特别适合处理医学图像分割中的小结构或不平衡类别。
- 公式为:
其中TP, FP, FN分别代表真正例、假正例和假负例。
-
Jaccard Loss(IoU Loss)
- Jaccard Loss基于Jaccard指数,也称为交并比(IoU)。这是评估分割质量的一个常用指标,计算预测分割区域和真实分割区域的交集与并集的比例。
- 它与Dice Loss类似,但在某些场合,Jaccard指数对边界不匹配的惩罚更大。
-
Tversky Loss
- Tversky Loss是Dice Loss的一种变体,允许对假正例和假负例的权重进行不对称调整,这在处理极不平衡的数据集时尤为有用。
-
组合损失
- 在实际应用中,为了同时兼顾不同的评价指标和性能,研究者可能会结合多种损失函数,如交叉熵和Dice损失的组合,以便更有效地训练模型。
-
Focal Loss
- Focal Loss是对交叉熵损失的一种改进,主要解决类别不平衡问题,通过减少对易分类样本的关注来提高模型对难分类样本的关注度。
选择损失函数
选择哪种损失函数取决于特定的应用场景、类别平衡、预期的分割性能等因素。例如,医学图像分割中常常偏好使用Dice Loss因其对小区域和边缘的高敏感性。而在需要强调全局准确性的情况下,结合交叉熵和IoU损失可能更为合适。
5.2图形分类的损失函数
在图像分类任务中,常用的损失函数主要基于预测类别和实际类别之间的差异。以下是一些常见的图像分类损失函数:
-
交叉熵损失(Cross-Entropy Loss)
这是图像分类中最常用的损失函数之一。对于二分类问题,它通常被称为二元交叉熵损失(Binary Cross-Entropy Loss)。对于多分类问题,它通常被称为多类交叉熵损失(Categorical Cross-Entropy Loss),其中预测的是一个多维概率分布。 -
稀疏交叉熵损失(Sparse Categorical Cross-Entropy Loss)
与普通交叉熵损失类似,但适用于稀疏标签表示(即标签以整数形式给出,而不是独热编码)。 -
平方误差损失(Mean Squared Error Loss, MSE Loss)
主要用于回归任务,但在某些分类场景中也可用。它计算预测值与实际值之间的均方差,用于评估模型性能。 -
KL散度损失(KL Divergence Loss)
KL散度衡量两个概率分布之间的差异。对于分类问题,如果有两个概率分布(例如模型预测分布和目标分布),KL散度可以作为损失函数使用。 -
焦点损失(Focal Loss)
这是一种改进的交叉熵损失函数,旨在解决类别不平衡问题。它通过减小对易分类样本的关注,增强对难分类样本的学习,适用于类别分布不平衡的情况。 -
对比损失(Contrastive Loss)
通常用于度量学习和孪生网络,它使得来自同一类的样本距离更近,来自不同类别的样本距离更远。 -
标签平滑损失(Label Smoothing Loss)
这是交叉熵损失的一种改进版本,在计算损失时引入了标签平滑,以减轻模型的过拟合风险。
不同的损失函数在图像分类任务中有各自的优势和劣势,选择适当的损失函数取决于数据集的特性、模型的结构和任务的具体需求。
5.3目标检测的损失函数
目标检测是计算机视觉领域中的一项任务,它涉及到检测图像中的多个目标,并预测每个目标的类别和位置。目标检测模型通常使用复合损失函数,这些损失函数同时考虑类别预测的准确性和边界框(bounding box)的精度。以下是一些常见的目标检测损失函数:
-
交叉熵损失(Cross-Entropy Loss)
用于类别预测。对于目标检测中的每个预测框,模型需要确定是否包含对象,以及对象的类别是什么。 -
均方误差损失(Mean Squared Error, MSE)
用于边界框的回归。这种损失函数衡量预测的边界框和真实边界框之间的差异。 -
IOU(交并比,Intersection over Union)损失或GIoU、DIoU、CIoU损失
这些损失函数基于交并比,即预测框和真实框之间的交集与并集的比例。GIoUGeneralized IOU), DIoU(Distance IOU)和CIoU(Complete IOU)是IOU损失的改进版本,它们在某些情况下可以提供更稳定的梯度和更好的收敛性能。 -
锚框损失(Anchor Box Losses)
在使用基于锚框的目标检测模型(如Faster R-CNN)时,这类损失函数对每个锚框执行分类和回归。 -
Focal Loss
由于目标检测中经常出现大量的负样本(即不包含目标的预测框),Focal Loss 被设计来加重对难以分类样本的关注,减少对容易分类样本的关注,从而解决类别不平衡问题。 -
Smooth L1 Loss
这是一种在目标检测中常用的边界框回归损失函数,它是L1损失的平滑版本,可以减少离群点对损失函数的影响,通常在边界框坐标预测中使用。 -
组合损失
在实际应用中,目标检测模型通常使用以上多种损失函数的组合,例如,在YOLO和SSD这类模型中,会同时使用交叉熵损失和均方误差损失或Smooth L1损失。
选择哪种损失函数取决于具体的目标检测模型和任务需求。各种损失函数的组合能够同时优化分类和定位任务,提高目标检测的整体性能。
5.4图形增强的损失函数
图像增强是一种旨在改善或改变图像视觉质量的技术。它可以用于提高图像的可视性、可用性或感兴趣特征的突出度。图像增强在计算机视觉和机器学习任务中有着广泛的应用。在使用深度学习进行图像增强时,需要定义适当的损失函数以优化模型性能。以下是一些常见的图像增强损失函数:
-
均方误差(Mean Squared Error, MSE)
衡量生成或增强后的图像与目标图像之间的像素差异。MSE计算两个图像每个像素之间的误差平方和的平均值。 -
平均绝对误差(Mean Absolute Error, MAE)
与MSE相似,但它计算的是每个像素的绝对误差的平均值。相对于MSE,MAE对异常值的敏感度较低。 -
结构相似性(Structural Similarity, SSIM)
用于衡量两幅图像之间的结构相似性。SSIM综合考虑了亮度、对比度和结构三个方面,使其在视觉质量上与人类视觉感知更为接近。 -
感知损失(Perceptual Loss)
通过使用预先训练的神经网络(如VGG网络)计算特征之间的差异,将图像的高级特征作为视觉相似度的衡量标准,使得增强后的图像在感知上更接近目标图像。 -
对抗性损失(Adversarial Loss)
在生成对抗网络(GAN)结构中,判别器会学习将生成的图像与真实图像区分开来。生成器的目标是生成尽可能真实的图像以欺骗判别器。这种损失通常与其他损失函数结合使用,以增强生成图像的真实性。 -
特定应用的损失函数
例如在超分辨率(Super-Resolution)任务中,可能使用多尺度结构相似性损失、多尺度对抗性损失等,以适应不同的图像质量评价需求。
这些损失函数或其组合通常用于各种图像增强任务中,包括图像超分辨率、去噪、着色、风格迁移等。损失函数的选择取决于具体的图像增强任务及其目标要求。
相关文章:
损失函数详解
1.损失函数 是一种衡量模型与数据吻合程度的算法。损失函数测量实际测量值和预测值之间差距的一种方式。损失函数的值越高预测就越错误,损失函数值越低则预测越接近真实值。对每个单独的观测(数据点)计算损失函数。将所有损失函数(loss function…...

算法提高之树的中心
算法提高之树的中心 核心思想:树形dp 换根dp 每个点作为根节点 找其子树的最大距离和父节点的最大距离 dfs1:求子树对于当前根节点的最大距离和次大距离 求次大距离原因:如果当前节点是其父节点子树的最大路径上的点,最大距离不…...
【Java基础】面向对象是什么
面向对象和面向过程的对比 类和对象 class Car{} 是描述对象(车)的类,属于引用数据类型用来描述对象具有的属性(变量)和行为(函数),属于概念模型 Car baomanew Car(); 对象需要由类来创建对象具备了类中定义的属性和行为 对象…...

家用洗地机应该怎么选?哪个牌子好?市场上主流洗地机品牌推荐
洗地机的出现,让越来越多的家庭享受清洁的过程,给人们腾出来更多的时间陪伴家人和休息。但是在选购一台洗地机前,大家多多少少肯定有些疑问,洗地机到底实不实用?好不好用?能扫干净吗?还有哪些好…...

python Django REST framework允许你根据API的版本提供不同的行为或数据
在Django REST framework中,版本控制是一个重要的功能,它允许你根据API的版本提供不同的行为或数据。以下是如何在Django REST framework中设置API版本控制的几种方法: 1. 使用URL路径参数 你可以通过URL路径中的参数来指定API的版本。例如: python复制 # urls.py from …...

unity给物体添加可以包裹所有子物体的BoxCollider
代码如下可直接调用 MeshTool.SpawnCollider(mode);using UnityEngine;public class MeshTool {public static Bounds SpawnCollider(Transform target){Vector3 pMax Vector3.zero;Vector3 pMin Vector3.zero;Vector3 center Vector3.zero;Vector3 oldPos target.transfor…...
2024五一数学建模A题思路代码与论文分析
2024五一数学建模A题完整代码和成品论文获取↓↓↓↓↓ https://www.yuque.com/u42168770/qv6z0d/gyoz9ou5upvkv6nx?singleDoc# 2024五一数学建模A题钢板最优切割路径问题需要建立的模型和算法: 图论 最短路径算法(Dijkstra算法、Floyd算法等) 动态规划 网格化离散建模 …...
ICode国际青少年编程竞赛- Python-1级训练场-基础训练2
ICode国际青少年编程竞赛- Python-1级训练场-基础训练2 1、 a 4 # 变量a存储的数字是4 Dev.step(a) # 因为变量a的值是4,所以Dev.step(a)就相当于Dev.step(4)2、 a 1 # 变量a的值为1 for i in range(4):Dev.step(a)Dev.turnLeft()a a 1 # 变量a的值变为…...

科技控必看!让你轻松成为机器人领域达人
科技控们注意了!你是不是经常对机器人技术充满无限的好奇,却又因为缺乏合适的渠道而难以深入了解和亲身体验呢?别担心,BFT机器人,正是你探索机器人世界的绝佳之地! 在这里,你将发现一个充满惊喜…...

Linux进程——Linux下常见的进程状态
前言:在进程学习这一块,我们主要学习的就是PCB这个进程控制块,而PBC就是用来描述进程的结构体,而进程状态就是PCB结构体中的一个变量。 本篇主要内容: 操作系统中的进程状态Linux下的进程状态 在开始之前,我…...

TCP长连接短链接
1、短连接 短连接是指通讯双方有数据交互时,就建立一个连接,数据发送完成后,则断开此连接,即每次连接只完成一项业务的发送。 2、长连接 长连接是指在一个连接上可以连续发送多个数据包,在连接保持期间,…...

代码随想录35期Day33-Java
Day33题目 LeetCode1005:K 次取反后最大化的数组和 核心思想:每次取反都取反最小的。如果有负数,则一直取反最小的负数,如果没有就取反正数。取反次数只需要看是奇数还是偶数。偶数则正数序列不变,奇数则最小的变成负数 class …...
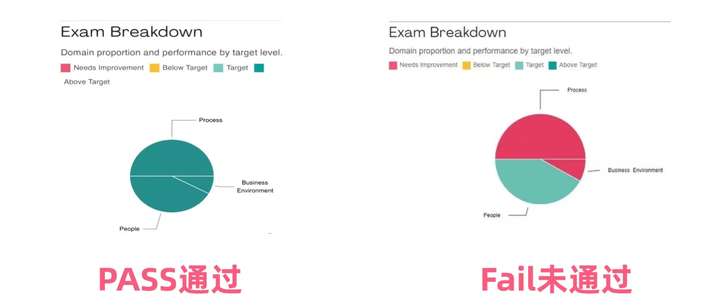
PMP考试没过怎么办?如何补考?(附复核流程)
最近刷小红书,看很多人都在晒PMP通过的成绩截图,一方面为大家开心,终于拿到了期盼已久的PMP,但同时也有宝子发挥失常没通过考试,所以这期针对没考过的宝子们,出一期复盘文章,无论结果如何&#…...
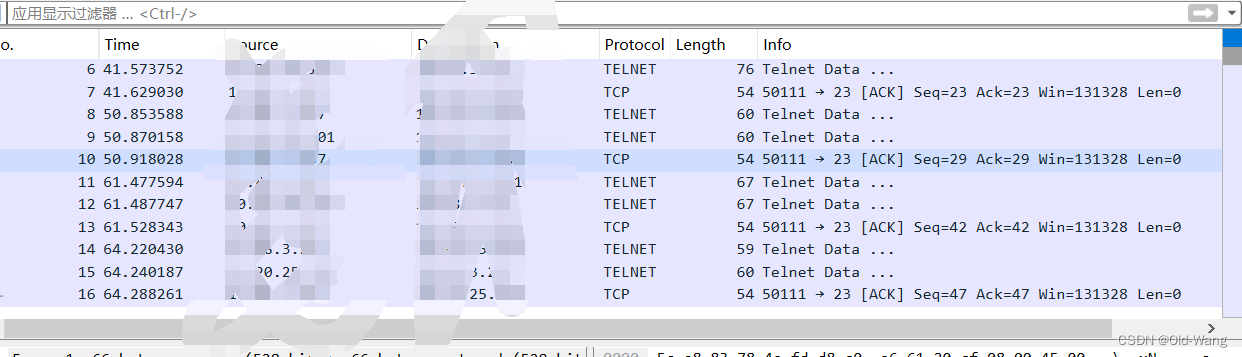
自主实现Telnet流量抓取
自主实现Telnet流量抓取 根据测试需求,需要抓取Telnet流量包,使用wireshark Python(socket、telnetlib库)实现 实现代码 主要此处有坑, 根据协议规则,wireshark 默认端口为23 的是Telnet协议࿰…...

以瓦片地图为底图添加图表,保留拖拽功能
1、问题1 在地图上覆盖一个容器层,容器层上的内容显示不出来如何解决? 原因:堆叠指数问题 解决方案:绝对定位后,提升其z-index值即可 2、问题2 在地图上覆盖一个容器层,影响了地图拖拽,如何…...

Windows cmd bat之特殊符号及变量
cmd 常用变量 bat批处理常用命令 %1~%9表示拖入文件(%0以外的输入文件),%0表示批处理文件本身 %0~%1字母意思基本相同,不区分大小写 ::打印当前窗口地址 echo “%cd%” %0 获取当前文件路径 %~d0 …...
用python写个控制MicroSIP自动拨号和定时呼叫功能(可用在小型酒店叫醒服务)
首先直接上结果吧,MicroSIP 助手,控制MicroSIP自动拨号,定时呼叫的非常实用小工具! 在使用MicroSIP 助手之前,我们需要了解MicroSIP是什么,MicroSIP是一个SIP拨号软件,支持注册任意SIP平台实现拨…...

axios 取消token 模糊搜索
import axios from ‘axios’; // 创建一个取消令牌源(cancel token source) const CancelToken axios.CancelToken; const source CancelToken.source(); // 下拉框搜索函数 function search() { // 获取输入值 const inputValue document.getElem…...

【OTS4WORD】“精简并行过程”——容易剪裁的“软件过程改进方法和规范”模板
附件资源是作者针对SPP采用模板重新格式化打包制作,原模板具有格式不受控的缺点,导致文档编制过程中引起不必要的排版麻烦。 附件资源适用于希望改进工作流程,适配CMMI质量管理体系的公司或个人使用,质量改进管理组织、项目管理组…...

22 | MySQL有哪些“饮鸩止渴”提高性能的方法?
短连接风暴 第一种方法:先处理掉那些占着连接但是不工作的线程。 kil id 第二种方法:减少连接过程的消耗。 让数据库跳过权限验证阶段,重启数据库,并使用–skip-grant-tables 参数启动。 慢查询性能问题 索引没有设计好 创建索引都支持 Online DDL 了,对于那种高峰期数…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...
