数据结构---时间复杂度+空间复杂度
算法(algorithm)简单说就是解决问题的方法。方法有好坏,同样算法也是,有效率高的算法,也有效率低的算法。衡量算法的好坏一般从时间和空间两个维度衡量,也就是本文要介绍的时间复杂度和空间复杂度。有些时候,时间与空间不可兼得,会出现以时间换空间或者以空间换时间
1.时间复杂度
I.时间复杂度概念
在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。一个算法所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?最简单的方法就是将算法运行一遍,但是运行时间容易受到环境、数据规模等的影响,所以才有了这个时间复杂度这个分析方式,一个算法所花费的时间与其中语句的执行次数成正比列,算法中的基本操作的执行次数,为算法的的时间复杂度。
找到某条基本语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度。
//请计算Fun1中++count语句总共执行了多少次
void Func1(int N)
{int count = 0;for (int i = 0; i < N; ++i){++count;}for (int k = 0; k< 2*N; ++k){++count;}int M = 0;while (M--){++count;}printf("%d\n",count);
}
Func1执行的基本操作次数:
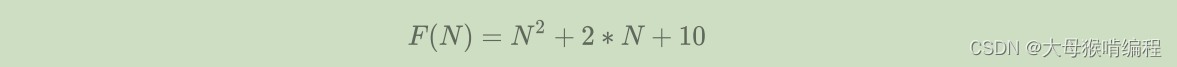
- N=10 F(N)=130
- N=100 F(N)=10210
- N=1000 F(N)=1002010
实际中计算时间复杂度时,其实并不一定要计算精确的执行次数,而只需要大概执行次数,因此在计算时使用大O渐近表示法。
II.大O渐近表示法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号
推导大O阶方法:
(1).用常数1取代运行时间中的所有加法常数
(2).在修改后的运行次数函数中,只保留最高阶项
(3).如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶
使用大O阶渐进表示法以后,Func1的时间复杂度是
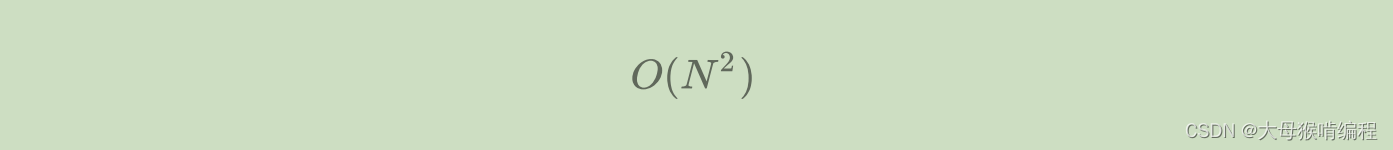
- N=10 F(N)=100
- N=100 F(N)=10000
- N=1000 F(N)=1000000
通过上面可以看出发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
另外有些算法的时间复杂度存在最好、平均和最坏情况:
- 最坏情况:任意输入规模的最大运行次数(上界)
- 平均情况:任意输入规模的期望运行次数
- 最好情况:任意输入规模的最小运行次数(下界)
比如说:在一个长度为N的数组中搜索一个数据x
最坏情况:N次找到
平均情况:N/2次找到
最好情况:1次找到
在实际中一般情况下关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
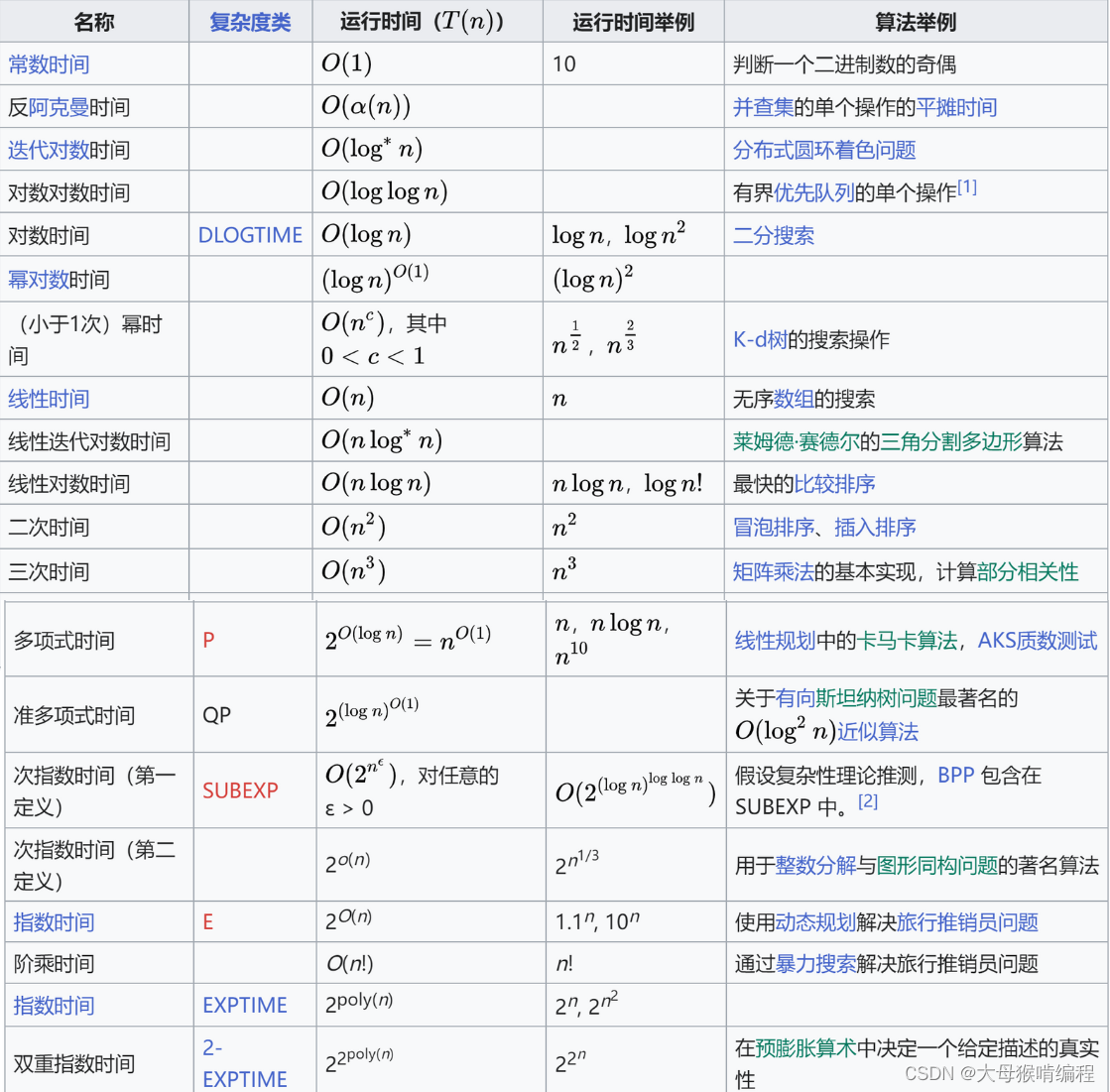
时间复杂度的计算是确定它的量级,通过确定不同的量级来比较算法的好坏,常见量级如下

完整的如下:
III.示例:
//计算Func2的时间复杂度
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}Func2中第一个循环循环2*N次,第二个while循环循环10次,用数学表达式写的结果就是F(N)=2*N+10 ,经过推导可得,2是系数和常数M对整体的影响较小,故最终的时间复杂度就是O(N)
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; M++){++count;}for (int k = 0; k < N; ++k){++count;}printf("%d\n", count);
}Func3中第一个循环循环M次,第二个循环循环M次,F(N)=M+N,对应的时间复杂度就是O(M+N)(Omax(M,N)),如果M远大于N,就是O(M),如果N远大于M,就是O(N)
void Func4(int N)
{int count = 0;for (int k = 0; k < N; ++k){++count;}printf("%d\n", count);
}Func4中只有一个循环,循环N次,时间复杂度就是O(N)
//计算strchr的时间复杂度
const char*strchr(const char *str,int charcter);最坏情况是O(N),最好的情况是O(1)
void Bubblesort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for(size_t i=1;i<end;++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
冒泡排序中,两层循环,外层循环控制每次遍历的范围,内层粗那混执行相邻的元素的比较和交换
- 外层循环的迭代次数为n,其中n是数组的长度
- 内层的迭代次数随外层循环的进行而减少,但是最坏情况下,内层迭代的次数也是n
因此,此方法的冒泡排序的时间复杂度为O(n^2)
long long Fac(size_t N)
{if (N == 0){return 1;}return Fac(N - 1) * N;
}
总共递归N次,数学表达式可写为F(N)=N+(N-1)+(N-2)+......+(1)+(0),时间复杂度就为O(N)
long long Fib(size_t N)
{if (N < 3){return 1;}return Fib(N - 1) + Fib(N - 2);
}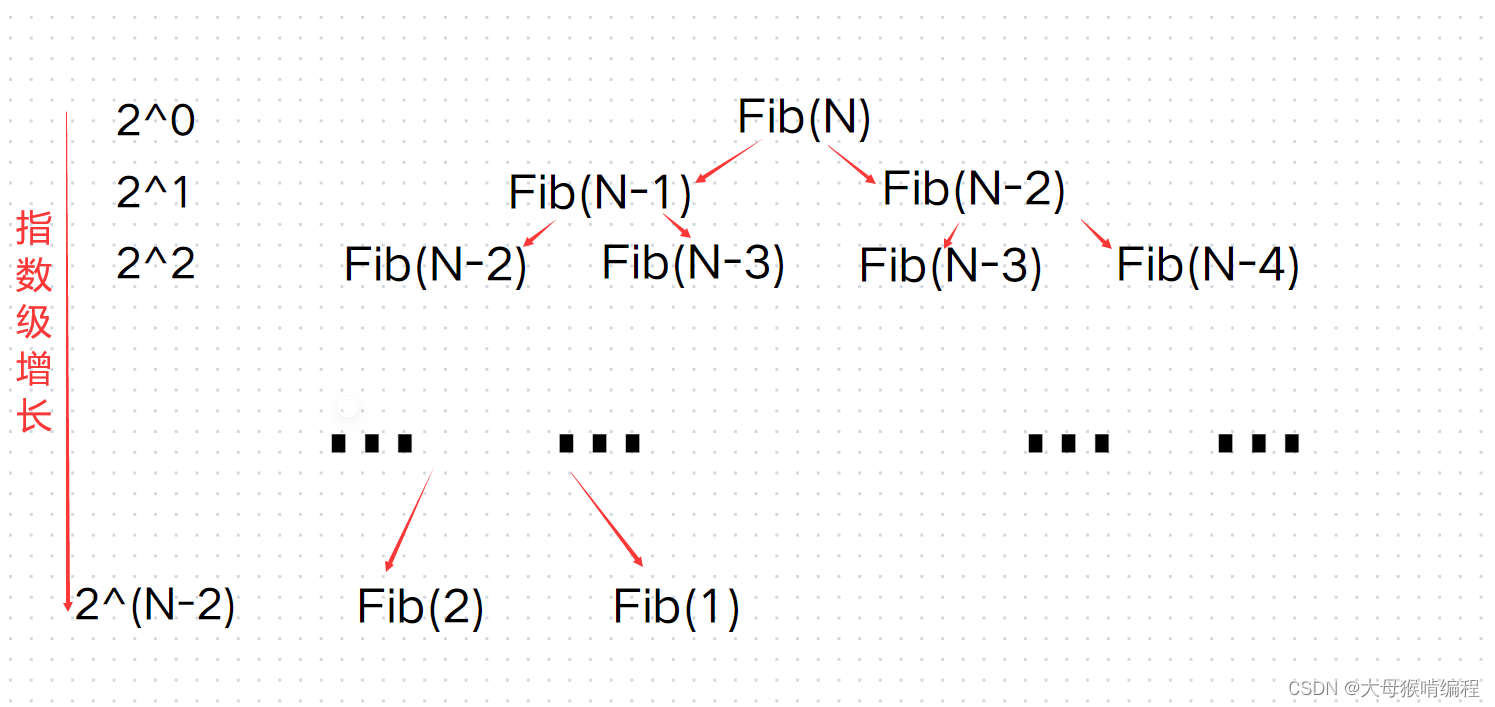
- 在每次的递归调用中,函数都会进行一次加法操作
- 递归的深度取决于输入参数N的大小
数学表达式可写作F(N)=2^(N-2),时间复杂度就为O(2^N)(关于斐波那契数列的时间复杂度,深入探讨见:http://递归求解斐波那契数列的时间复杂度——几种简洁证明 - SleepyBag的文章 - 知乎 https://zhuanlan.zhihu.com/p/257214075)
2.空间复杂度
I.空间复杂度概念
空间复杂度也是有个数学表达式,是对一个算法在运行过程中临时占用储存空间大小的量度。
空间复杂度不是程序占用了多少bytes的空间,因为这个没有实际意义,所以空间复杂度是变量的个数,空间复杂度计算规则基本跟时间复杂度类似,也是采用大O渐近表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显示申请的额外空间来确定。
就像时间复杂度的计算不考虑算法所使用的空间大小一样,空间复杂度也不考虑算法运行需要的时间长短,空间复杂度计算的是算法中额外的空间
II.示例:
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int tmp = 0;for (size_t i = 0; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);tmp = 1;}}if (tmp == 0)break;}
}在冒泡排序中,变量的个数只有end、tmp、i三个,是确定的,所以空间复杂度是O(1)(数组中的空间不计入,不属于算法中额外开辟的空间)
long long* Fibonacci(size_t n)
{if (n == 0){return NULL;}long long* fibArray = (long long)malloc((n + 1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i < n; ++i){fibArray[i] = fibArray[i - 1] + fibArray[i - 2];}return fibArray;
}上述代码中在求斐波那契额数列的过程中开辟了数列,这个数列属于额开辟的空间,此外,还有一个变量n,综上,空间复杂度为O(N)
long long Fac(size_t N)
{if (N == 0){return 1;}return Fac(N - 1) * N;
}上述代码并没有创建变量,但是每次函数的调用都需要创建函数栈帧,这个算法调用了N次(具体取决于递归深度),所以空间复杂度是O(N)
相关文章:

数据结构---时间复杂度+空间复杂度
算法(algorithm)简单说就是解决问题的方法。方法有好坏,同样算法也是,有效率高的算法,也有效率低的算法。衡量算法的好坏一般从时间和空间两个维度衡量,也就是本文要介绍的时间复杂度和空间复杂度。有些时候,时间与空间…...

Verilog 触发器状态机语言描述
触发器状态机语言描述 触发器状态机语言用于描述映射到 ILA 调试核的高级触发器逻辑的复杂触发条件。触发器状态机具有下列特性 : • 最多 16 种状态。 • 用于复杂状态转换的单向、双向和三向条件分支。 • 4 个内置 16 位计数器 , 用于对事件…...

等保保护测评试题中
二、多选题 1、防火墙提供的接入模式中包括(ABCD) A.网关模式 B.透明模式 C.混合模式 D.旁路接入模式 2、不同设VLAN之间要进行通信,可以通过 .(AB) A.交换机 B.路由器 C.网闸 D.入侵检测 E.入侵防御系统…...

SD-Turbo部署
stabilityai/sd-turbo 官网 2023 年 11 月 30 日 继推出 SDXL-Turbo 之后,我们又发布了SD-Turbo。 2023 年 11 月 28 日 我们正在发布 SDXL-Turbo,一种闪电般快速的文本到图像模型。除了模型之外,我们还发布了技术报告 用法࿱…...
(Java))
【ZZULIOJ】1095: 时间间隔(函数专题)(Java)
目录 题目描述 输入 输出 样例输入 Copy 样例输出 Copy 提示 code 题目描述 从键盘输入两个时间点(24小时制),输出两个时间点之间的时间间隔,时间间隔用“小时:分钟:秒”表示。要求程序定义如下两个函数,并在main()中调用…...

Rust:文件 launch.json 有什么用?
launch.json 是 Visual Studio Code(VSCode)中的一个配置文件,主要用于配置调试器。当你在 VSCode 中进行代码调试时,launch.json 文件告诉调试器如何启动和配置你的程序。 具体来说,launch.json 文件包含了以下信息&…...

vue3实现文字垂直滚动
在Vue 3中实现文字的垂直滚动,你可以使用CSS动画或者JavaScript来控制滚动行为。以下是一个简单的Vue 3组件示例,该组件使用CSS的keyframes动画来实现文字的垂直滚动效果: <template> <div class"vertical-scroll-text"&…...

Android4.4真机移植过程笔记(三)
如果文章字体看得不是很清楚,大家可以下载pdf文档查看,文档已上传~oo~ 7、安装加密APK 需要修改文件如下: 相对Android4.2改动还是蛮大的,有些文件连路径都变了: //Android4.2 1、frameworks/native/libs…...

PostgreSQL备份恢复与复制
前言 随着国家战略层面对信息安全关注度越来越高,数据库是基础软件国产化自主可控的重要方面之一。PG是世界上最流行的开源关系型数据库之一,并且他是类BSD开源许可,开源协议非常友好,可以随意分发、闭源和开源,可以用…...
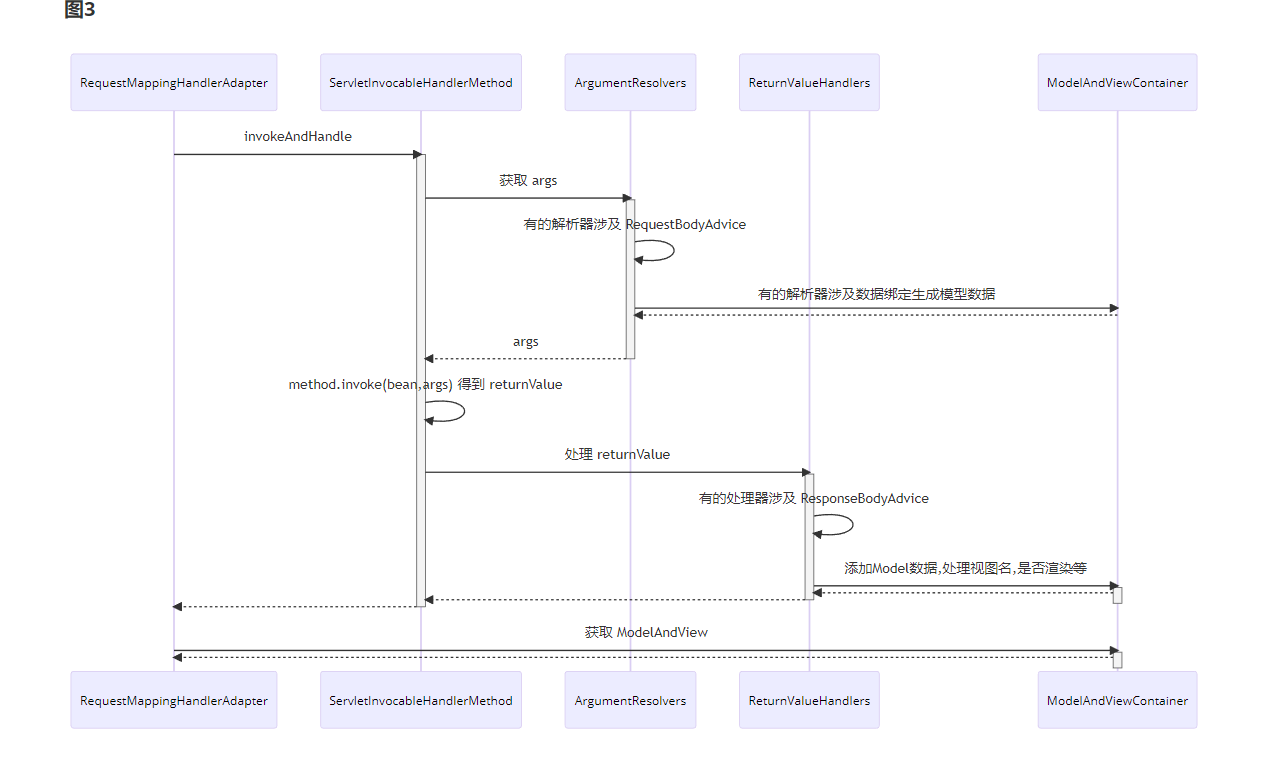
spring高级篇(八)
本篇对Spring MVC 的执行流程做一个简单总结 MVC执行流程总结 当浏览器发送一个请求,例如http://localhost:8080/hello,请求到达服务器后,一般会进行如下操作: 1、首先会经过DispatcherServlet,默认映射路径为 /&…...
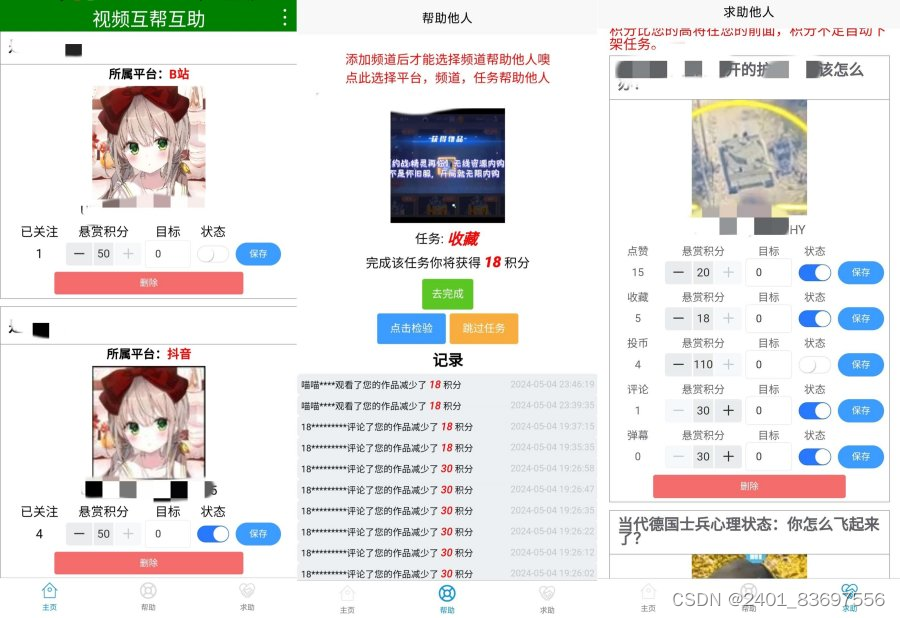
UP互助 帮助UP起号做视频 支持B站和抖音
【软件名字】:UP互助 【软件版本】:1.0 【软件大小】:17.5MB 【软件平台】:安卓 【测试机型】:小米9 1.随便登个邮箱,添加自己平台的频道,然后就可以帮助别人,添加频道后在添加…...
?)
*求问?:为何会超时(TLE)?
D - Grid and Magnet (atcoder.jp) 错误代码: //2024年5月5日14:53:43 #include <bits/stdc.h> #define move mmove //防止与头文件中重复 using namespace std; int h,w; string s[1000]; const int move[4][2]{{1,0},{-1,0},{0,1},{0,-1}}; bool used[100…...
维护问题)
cocosstudio工程文件(.ccs)维护问题
创建cocos工程.bat在多人合作的cocos项目中,大家公用一个ccs文件,存在的问题是如果大家都提交ccs文件比较容易出现冲突,解决冲突麻烦要耗费时间,不提交的话就拉不到其他人更新的csd文件。 方案一 解决冲突,更新提交c…...
Blender动画与云渲染:创造高质量作品的未来路径
Blender作为开源的3D图形软件,在多个领域广受欢迎。但随着项目复杂度提升,传统渲染方式受限。云渲染技术的兴起突破了这些限制,为创作者提供了更自由、高效的创作环境。 一、Blender动画项目的挑战 传统上,Blender动画渲染需要依…...

【MySQL】3.MySQL核心概念解析:数据完整性、事务处理、索引及聚簇索引与非聚簇索引
探索MySQL的内部机制,理解数据完整性、事务处理、索引策略以及聚簇索引与非聚簇索引的区别是至关重要的。这些概念构成了数据库设计和优化的基础,对于确保数据的准确性、提高查询效率、维护数据的一致性和实现复杂的数据库操作至关重要。本文将逐一剖析这…...
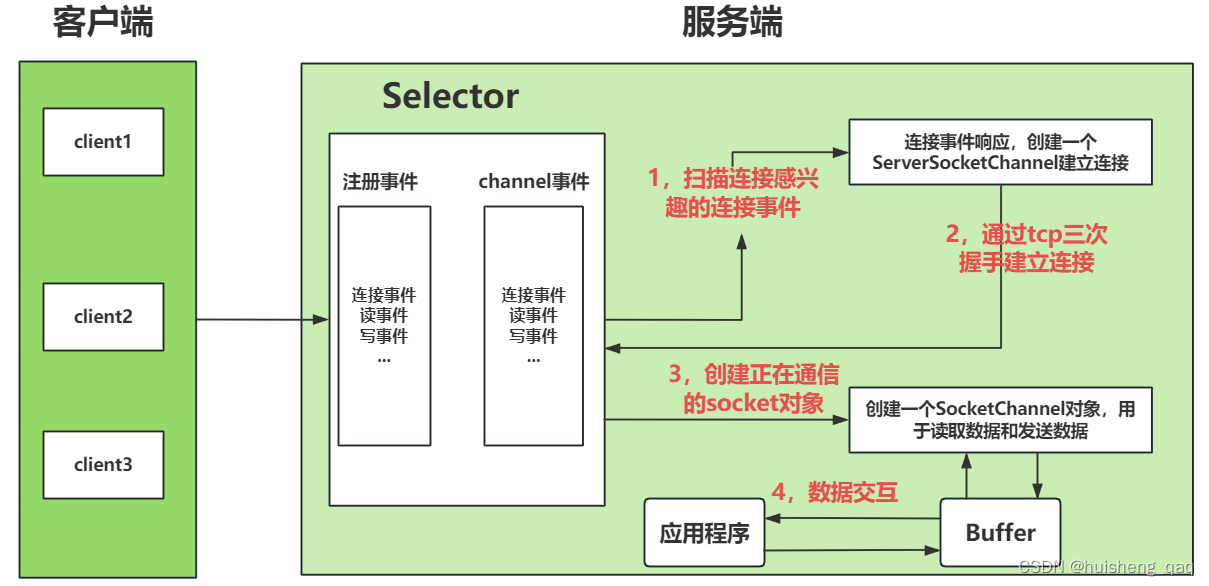
【netty系列-03】深入理解NIO的基本原理和底层实现(详解)
Netty系列整体栏目 内容链接地址【一】深入理解网络通信基本原理和tcp/ip协议https://zhenghuisheng.blog.csdn.net/article/details/136359640【二】深入理解Socket本质和BIOhttps://zhenghuisheng.blog.csdn.net/article/details/136549478【三】深入理解NIO的基本原理和底层…...

大数据Scala教程从入门到精通第二篇:Scala入门
一:Scala入门 1:为什么学习Scala Spark新一代内存级大数据计算框架,是大数据的重要内容 Spark就是使用Scala编写的。因此为了更好的学习Spark,需要掌握Scala这门语言 Spark的兴起,带动Scala语言的发展! 2:Scala的发展…...
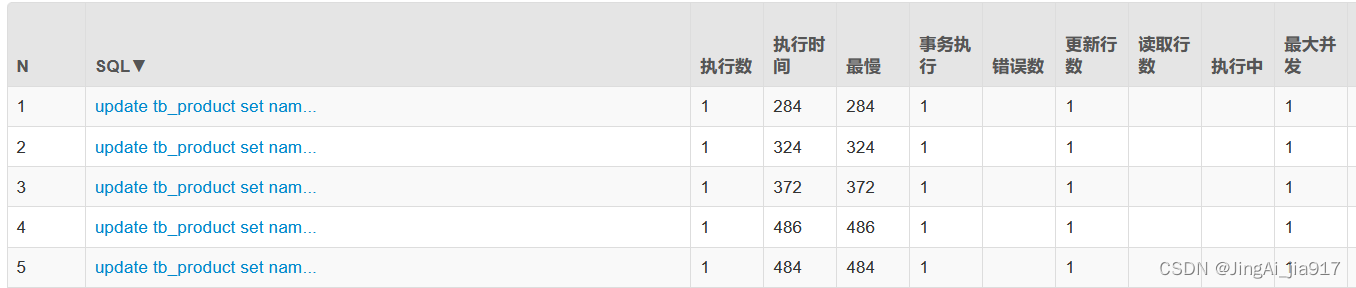
Spring Data JPA数据批量插入、批量更新真的用对了吗
Spring Data JPA系列 1、SpringBoot集成JPA及基本使用 2、Spring Data JPA Criteria查询、部分字段查询 3、Spring Data JPA数据批量插入、批量更新真的用对了吗 4、Spring Data JPA的一对一、LazyInitializationException异常、一对多、多对多操作 前言 在前两篇文章已经…...

数据结构-线性表-应用题-2.2-12
1)算法的基本设计思想:依次扫描数组的每一个元素,将第一个遇到的整数num保存到c中,count记为1,若遇到的下一个整数还是等于num,count,否则count--,当计数减到0时,将遇到的下一个整数保存到c中,计…...
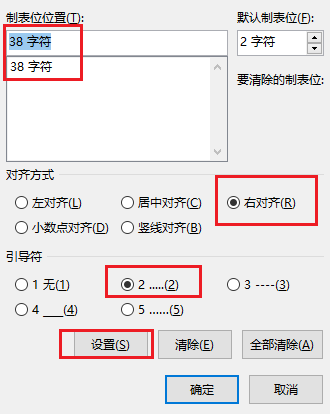
目录页码右对齐快速解决
选择目录–段落–制表符,按图中设置即可...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...
