力扣hot100:199. 二叉树的右视图/437. 路径总和 III(dfs/回溯/树上前缀和/哈希表)
文章目录
- 一、LeetCode:199. 二叉树的右视图
- 二、LeetCode:437. 路径总和 III
一、LeetCode:199. 二叉树的右视图
LeetCode:199. 二叉树的右视图

差点因为是个中等题打退堂鼓。其实比较简单。
右视图实际上只需要找到,每一层的最右边的那个结点即可。
dfs:
- 确保每次找到底层最右边的结点,时间复杂度 O ( n ) O(n) O(n)
class Solution {
public:vector<int> rightSideView(TreeNode* root) {cur_floor = 0;rightNode(root,0);return ans;}
private:void rightNode(TreeNode * root,int floor){//找到当前层最靠右的结点if(!root) return;if(floor == cur_floor){ans.emplace_back(root->val);cur_floor++;}rightNode(root->right,floor + 1);rightNode(root->left, floor + 1);return;}int cur_floor;vector<int> ans;
};
实际上使用层序遍历更好理解,每次选择一层的最后一个节点就行!
二、LeetCode:437. 路径总和 III
LeetCode:437. 路径总和 III
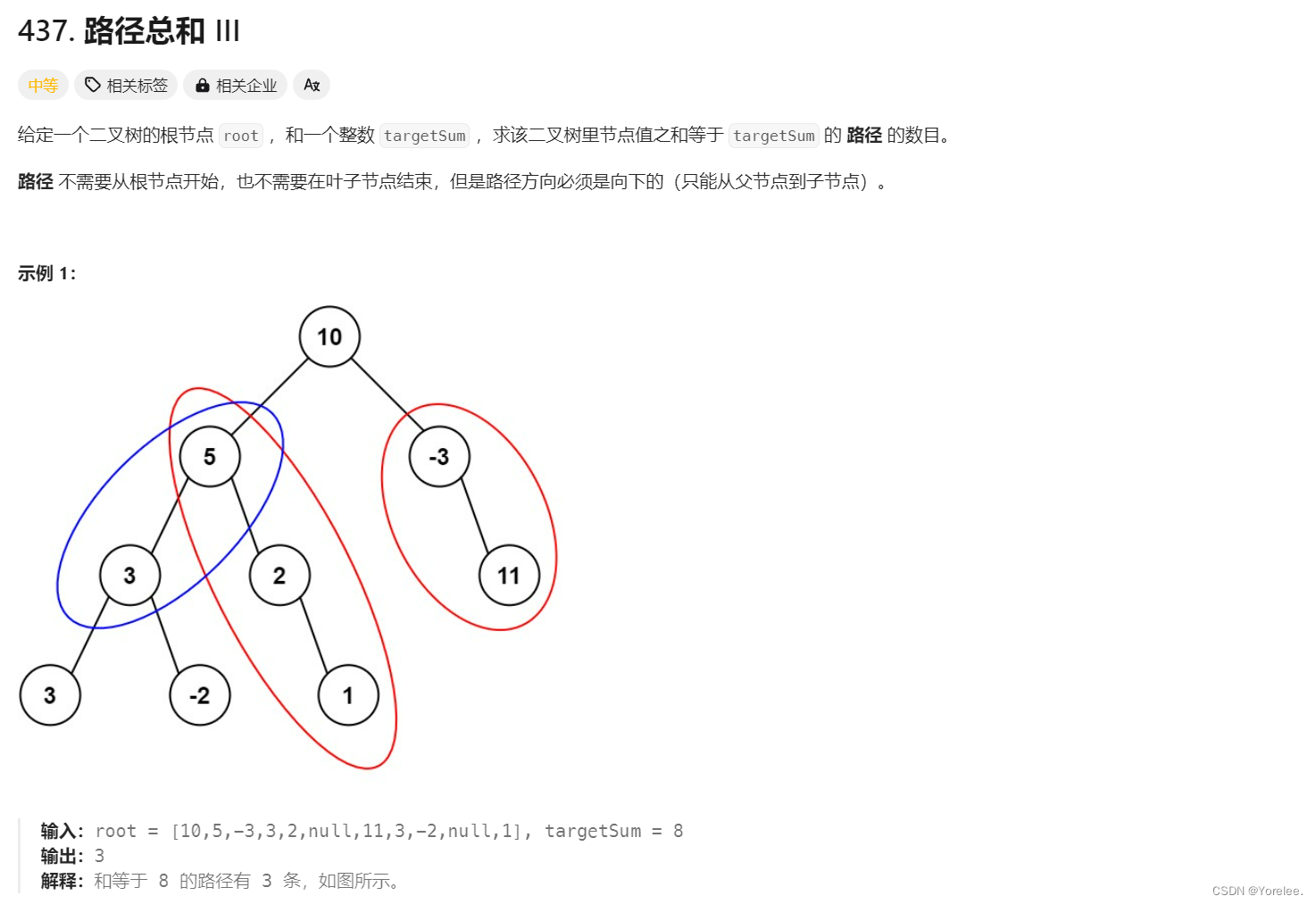
这个问题使用dfs可以解决,不过实现起来比较复杂,时间复杂度是 O ( n 2 ) O(n^2) O(n2)。我们先考虑其他方法。
发现使用树上前缀和很容易解决,最坏时间复杂度也是 O ( n 2 ) O(n^2) O(n2),所以我们先考虑使用前缀和。
未优化的前缀和+dfs回溯:
- 最坏时间复杂度是 O ( n 2 ) O(n^2) O(n2)
- 前缀和求和,需要考虑元素大小的问题,所以要使用
long long! - 对于每一个结点需要求其前缀和,以及以当前结点结尾的序列的值的总和是否存在等于
targetSum的 - 向下递归左右子节点,向上回溯。
class Solution {
public:int pathSum(TreeNode* root, int targetSum) {if(!root) return 0;vector<long long> presum;presum.emplace_back(0);//导入前导0getNum(root,targetSum,presum);return Num;}
private:void getNum(TreeNode * root,int targetSum,vector<long long> & presum){if(!root) return;//压入当前值的前缀和presum.emplace_back(root->val + presum.back());//判断以当前结点结尾的序列是否存在targetSum,由于存在负值,因此无法提前breakfor(int i = presum.size() - 2;i >= 0;--i){if(presum.back() - presum.at(i) == targetSum){++Num;}}//继续向下递归getNum(root->left,targetSum,presum);getNum(root->right,targetSum,presum);//弹出当前值回溯presum.pop_back();return;}int Num=0;
};
做过两数之和之后很容易想到使用哈希表直接查找使用存在所需要的值。
- p r e s u m 1 − p r e s u m 2 = t a r g e t S u m presum1 - presum2 = targetSum presum1−presum2=targetSum
- 则 p r e s u m 2 = p r e s u m 1 − t a r g e t S u m presum2 = presum1 - targetSum presum2=presum1−targetSum
我们真的是需要哈希表找到需要的值吗?在这里我们只需要之前有多少个这样的值就行了!
因此哈希的key = 目标前缀和,value = 目标前缀和的个数
使用哈希优化的前缀和+dfs回溯:
- 哈希查找,每个结点查找一次,平均时间复杂度 O ( 1 ) O(1) O(1),整个时间复杂度为 O ( n ) O(n) O(n)
- 使用
std::unordered_map的count方法,返回值是0或1表示存在或不存在。 - 必须先判断是否存在所需前缀和,再压入当前值。 原因是当前值和所需前缀和可能刚好相等,导致当前前缀和也变成了答案的一部分,但实际上它不能是答案的一部分相当于之前所说的是同一个前缀和了,这使得序列为空。
class Solution {
public:int pathSum(TreeNode* root, int target) {if(!root) return 0;targetSum = target;presum_num[0] = 1;//导入前导0getNum(root,0);return Num;}
private:void getNum(TreeNode * root,long long presum){if(!root) return;long long cur_presum = presum + root->val;//判断以当前结点结尾的序列是否存在targetSumif(presum_num.count(cur_presum - targetSum) != 0)Num += presum_num[cur_presum - targetSum];//压入当前值的前缀和presum_num[cur_presum]++;//继续向下递归getNum(root->left,cur_presum);getNum(root->right,cur_presum);//弹出当前值回溯if(presum_num[cur_presum] != 1) presum_num[cur_presum]--;else presum_num.erase(cur_presum);return;}int Num=0;int targetSum;unordered_map<long long,int> presum_num;
};
前缀和的方法如果之前接触过很容易想到,不过这里建议学习深度优先遍历的方法,更深入理解dfs。
dfs:
- 时间复杂度: O ( n 2 ) O(n^2) O(n2)
- 实现两个递归函数:
- 第一个函数
dfs:以根结点开始向下求和,得到targetSum则Num++ - 第二个函数
getNum:遍历所有树节点,每个结点调用dfs函数。
- 第一个函数
class Solution {
public:int pathSum(TreeNode* root, int target) {targetSum = target;getNum(root);return Num;}
private:void getNum(TreeNode * root){if(!root) return;dfs(root,0);//包含本结点向下递归getNum(root->left);getNum(root->right);return;}void dfs(TreeNode * root,long long sum){if(!root) return;if(root->val + sum == targetSum) Num++;dfs(root->left,sum + root->val);dfs(root->right,sum + root->val);return;}int Num = 0;int targetSum;
};
相关文章:

力扣hot100:199. 二叉树的右视图/437. 路径总和 III(dfs/回溯/树上前缀和/哈希表)
文章目录 一、LeetCode:199. 二叉树的右视图二、LeetCode:437. 路径总和 III 一、LeetCode:199. 二叉树的右视图 LeetCode:199. 二叉树的右视图 差点因为是个中等题打退堂鼓。其实比较简单。 右视图实际上只需要找到,…...

浅谈 HTTPS
文章目录 HTTPS 简介HTTPS 特点HTTPS 缺点与 HTTP 的区别HTTPS 工作流程1. 服务端生成密钥对2. 服务端申请数字证书3. 服务端发送数字证书4. 客户端验证数字证书5. 客户端解析证书内容6. 客户端传送加密信息7. 服务端解密信息8. 双方协商生成会话密钥并交换9. 使用会话密钥进行…...

js手动实现unshift
js 手动实现数组的unshift unshift是什么? unshift() 方法可向数组的开头添加一个或更多元素,并返回新的长度。 注意: 该方法将改变数组的数目。 语法: array.unshift(item1,item2, ..., itemX)代码实现 首先,在…...
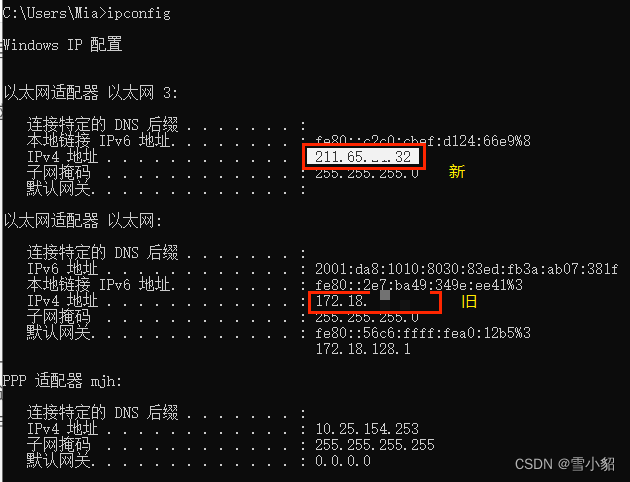
Failed to get DISPLAY: Error: All configured authentication methods failed 解决方法
Vscode一连接远程服务器就报错: 这个时候我们是无法使用Xming显示图像的。 尝试后发现,Windows电脑能够ping通服务器ip,但是服务器ping不通Windows电脑: 在网上查攻略,设置Windows电脑ip地址白名单,但…...
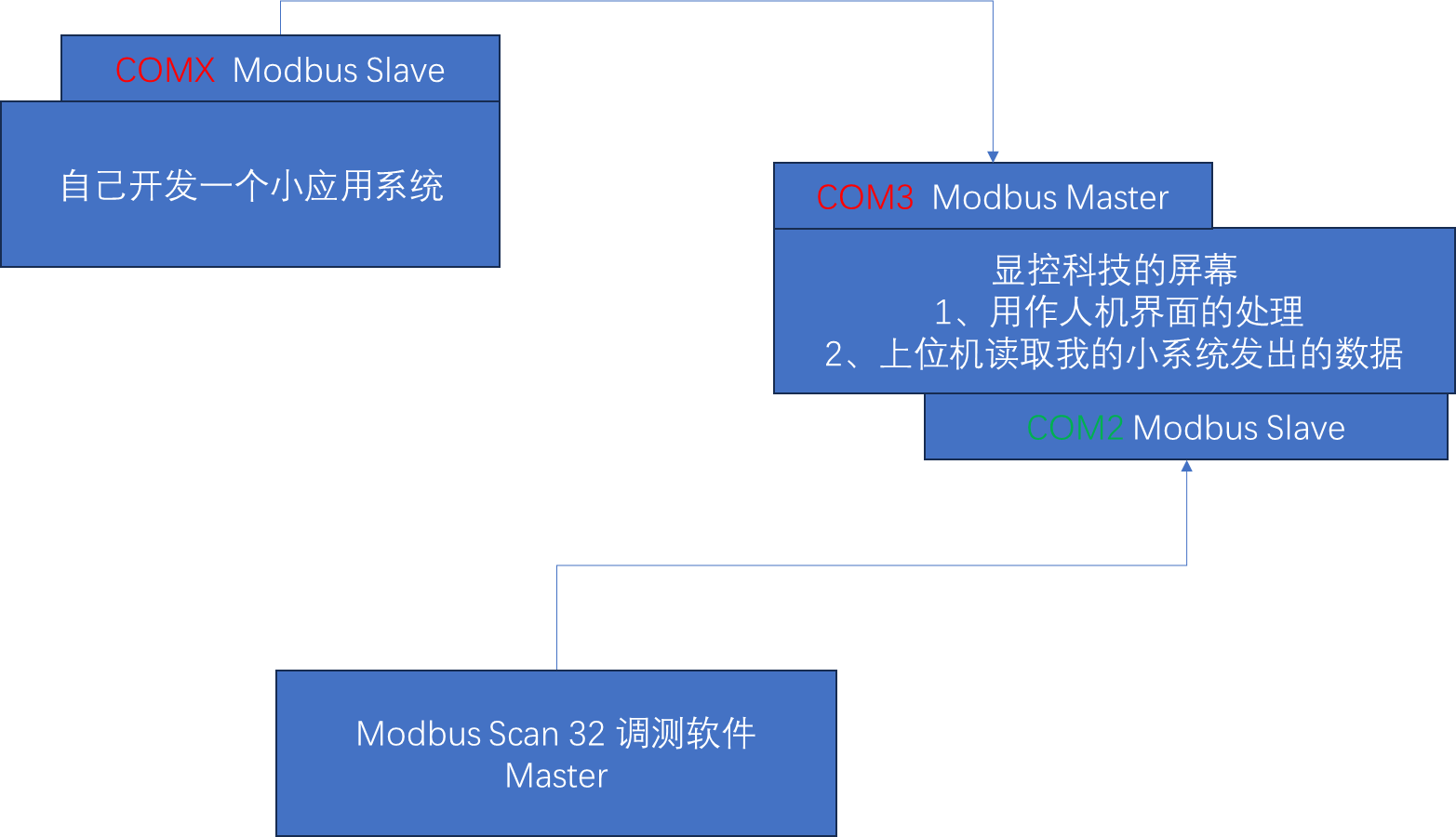
随便聊一下 显控科技 控制屏 通过 RS485 接口 上位机 通讯 说明
系统搭建: 1、自己研发的一个小系统(采集信号,将采集的信号数字化)通过COM口,连接显控屏 COM3 口采用 485 协议送到显控屏(显控科技)的显示屏展示出来)。 2、显控屏 将 展示的数据…...
)
C++学习笔记(多线程)
Multithreading 1、线程的基本操作1.1、创建线程1.2、等待线程和分离线程1.3、获取线程id 2、互斥锁3、条件变量4、例程 1、线程的基本操作 从C11开始推出关于多线程的库和函数,相比于Linux所配套的资源,C11提供的函数更加容易理解和操作,对…...
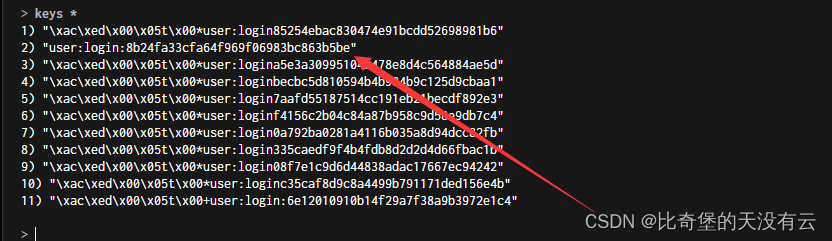
解决Redis的键值前出现类似\xAC\xED\x00\x05t\x00*这样的字符序列
文章目录 1.问题2.解决方法3.StringRedisTemplate和RedisTemplate的区别 1.问题 在使用RedisTemplate对Redis进行操作时,发现Reids键值对前有\xAC\xED\x00\x05t\x00*这样的字符序列 如图所示: 虽说不影响使用,但是听影响观感的 2.解决方法 查找了很多方法,可以指定RedisTem…...

分享 Kamailio 5.7.x 预处理一例
来自工单,很不错 不翻译了,认真看的话都能看懂 #!define IPADDR 127.0.0.1 #!defexp SIPURI "sip:" IPADDR ":5060" #!defexp QSIPURI "sip: IPADDR :5060" #!defexp V16 1<<4 Another possibility is using…...
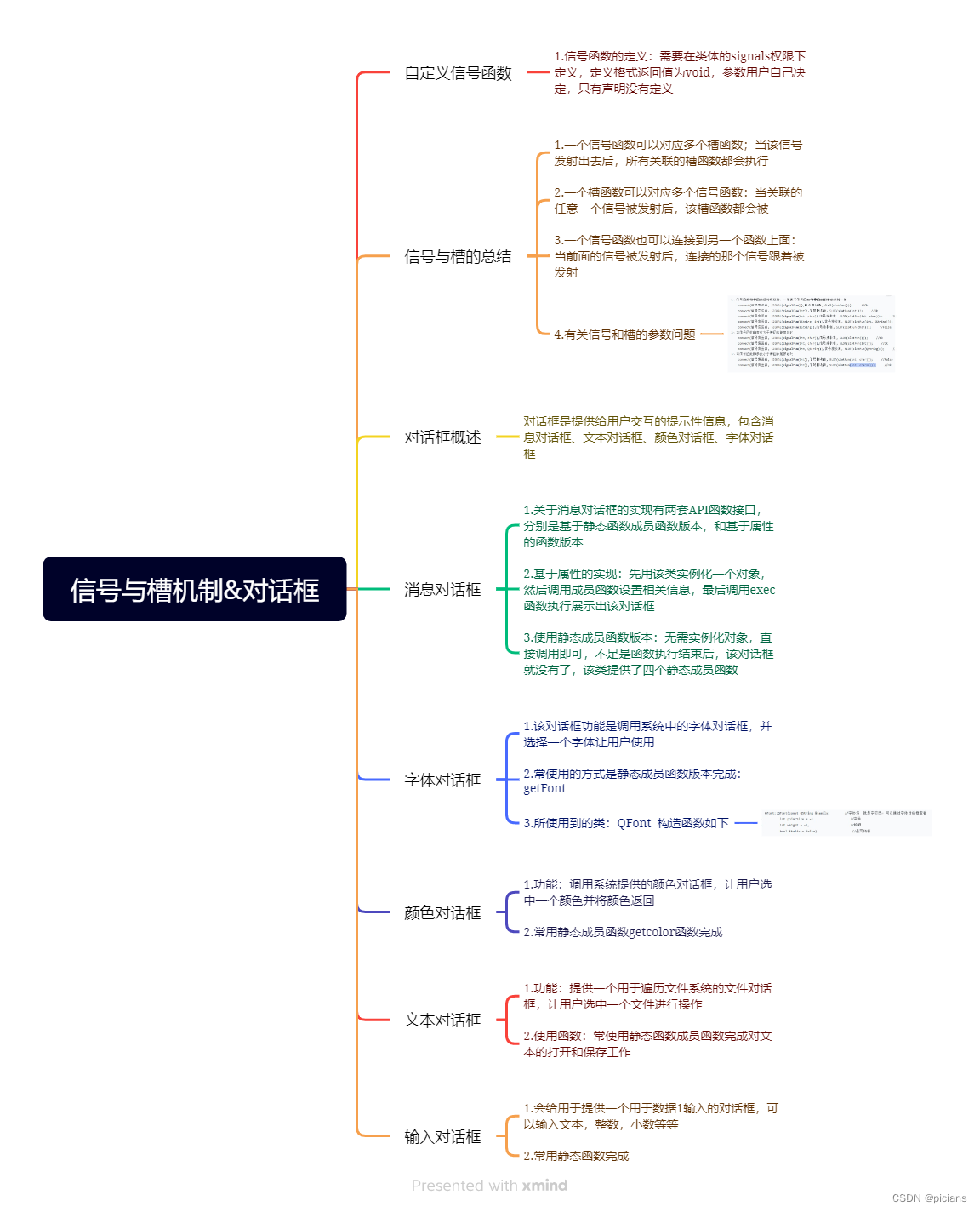
学QT的第三天~
ikun登录界面完善 #include "mywidget.h" void MyWidget::bth1() { if(edit3 ->text()"520cxk"&&edit4 ->text()"1314520") { //1.实例化一个QmessageBox类的对象 QMessageBox box(QMessageBox::Information, //图标 "恭喜…...
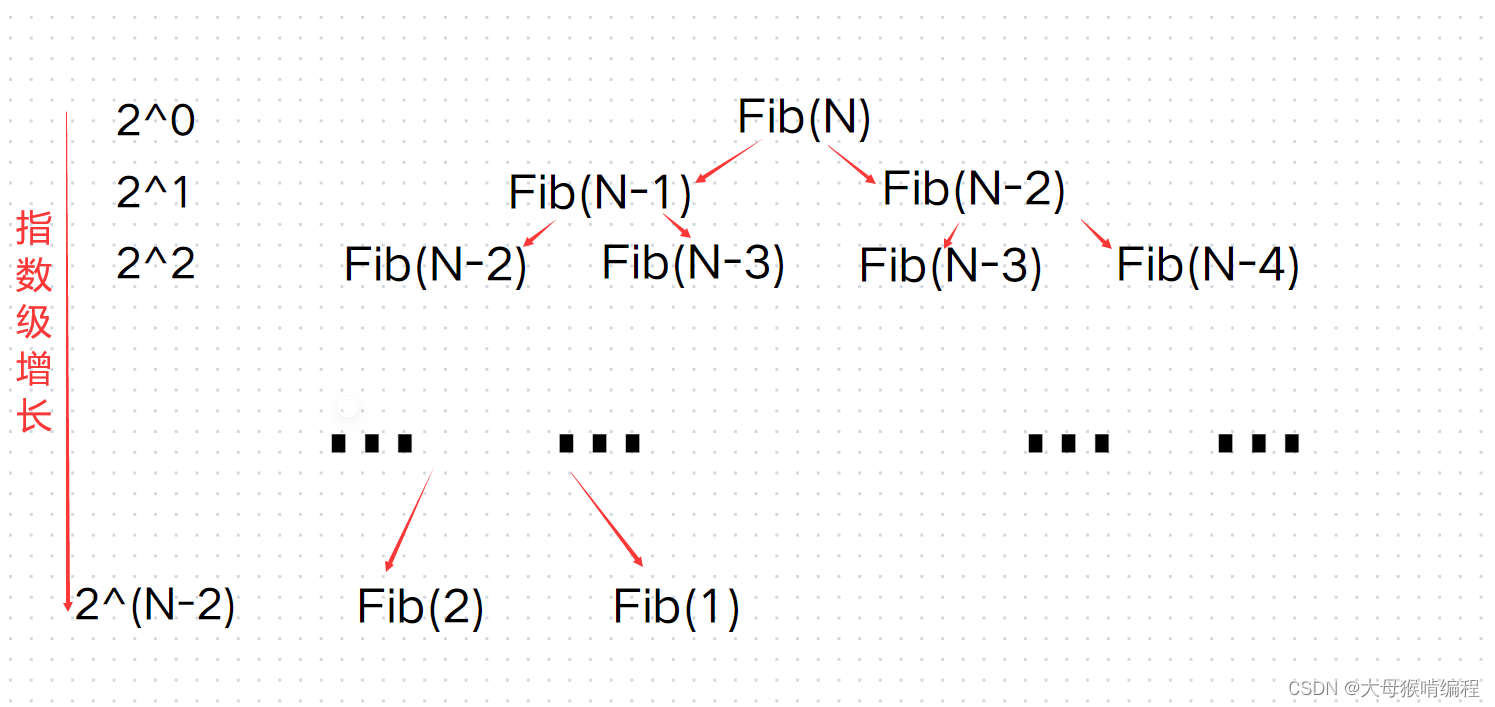
数据结构---时间复杂度+空间复杂度
算法(algorithm)简单说就是解决问题的方法。方法有好坏,同样算法也是,有效率高的算法,也有效率低的算法。衡量算法的好坏一般从时间和空间两个维度衡量,也就是本文要介绍的时间复杂度和空间复杂度。有些时候,时间与空间…...

Verilog 触发器状态机语言描述
触发器状态机语言描述 触发器状态机语言用于描述映射到 ILA 调试核的高级触发器逻辑的复杂触发条件。触发器状态机具有下列特性 : • 最多 16 种状态。 • 用于复杂状态转换的单向、双向和三向条件分支。 • 4 个内置 16 位计数器 , 用于对事件…...

等保保护测评试题中
二、多选题 1、防火墙提供的接入模式中包括(ABCD) A.网关模式 B.透明模式 C.混合模式 D.旁路接入模式 2、不同设VLAN之间要进行通信,可以通过 .(AB) A.交换机 B.路由器 C.网闸 D.入侵检测 E.入侵防御系统…...

SD-Turbo部署
stabilityai/sd-turbo 官网 2023 年 11 月 30 日 继推出 SDXL-Turbo 之后,我们又发布了SD-Turbo。 2023 年 11 月 28 日 我们正在发布 SDXL-Turbo,一种闪电般快速的文本到图像模型。除了模型之外,我们还发布了技术报告 用法࿱…...
(Java))
【ZZULIOJ】1095: 时间间隔(函数专题)(Java)
目录 题目描述 输入 输出 样例输入 Copy 样例输出 Copy 提示 code 题目描述 从键盘输入两个时间点(24小时制),输出两个时间点之间的时间间隔,时间间隔用“小时:分钟:秒”表示。要求程序定义如下两个函数,并在main()中调用…...

Rust:文件 launch.json 有什么用?
launch.json 是 Visual Studio Code(VSCode)中的一个配置文件,主要用于配置调试器。当你在 VSCode 中进行代码调试时,launch.json 文件告诉调试器如何启动和配置你的程序。 具体来说,launch.json 文件包含了以下信息&…...

vue3实现文字垂直滚动
在Vue 3中实现文字的垂直滚动,你可以使用CSS动画或者JavaScript来控制滚动行为。以下是一个简单的Vue 3组件示例,该组件使用CSS的keyframes动画来实现文字的垂直滚动效果: <template> <div class"vertical-scroll-text"&…...

Android4.4真机移植过程笔记(三)
如果文章字体看得不是很清楚,大家可以下载pdf文档查看,文档已上传~oo~ 7、安装加密APK 需要修改文件如下: 相对Android4.2改动还是蛮大的,有些文件连路径都变了: //Android4.2 1、frameworks/native/libs…...

PostgreSQL备份恢复与复制
前言 随着国家战略层面对信息安全关注度越来越高,数据库是基础软件国产化自主可控的重要方面之一。PG是世界上最流行的开源关系型数据库之一,并且他是类BSD开源许可,开源协议非常友好,可以随意分发、闭源和开源,可以用…...
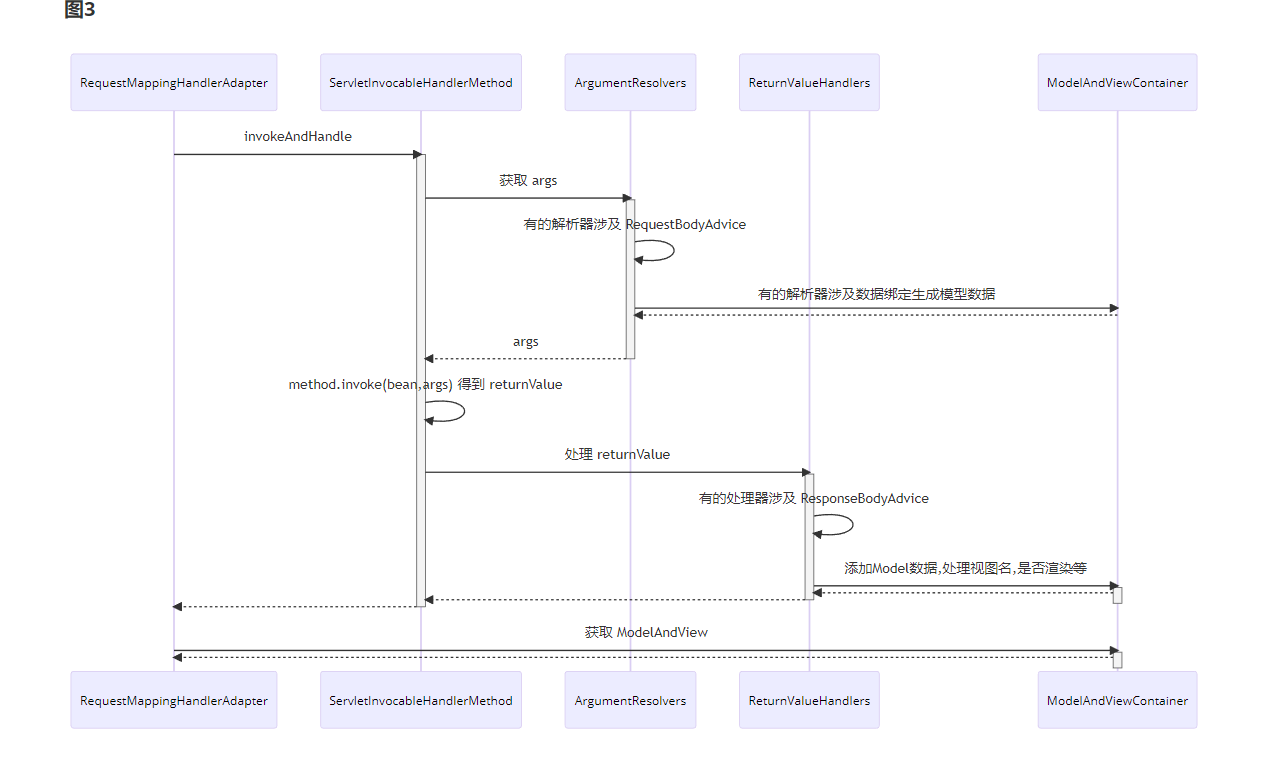
spring高级篇(八)
本篇对Spring MVC 的执行流程做一个简单总结 MVC执行流程总结 当浏览器发送一个请求,例如http://localhost:8080/hello,请求到达服务器后,一般会进行如下操作: 1、首先会经过DispatcherServlet,默认映射路径为 /&…...
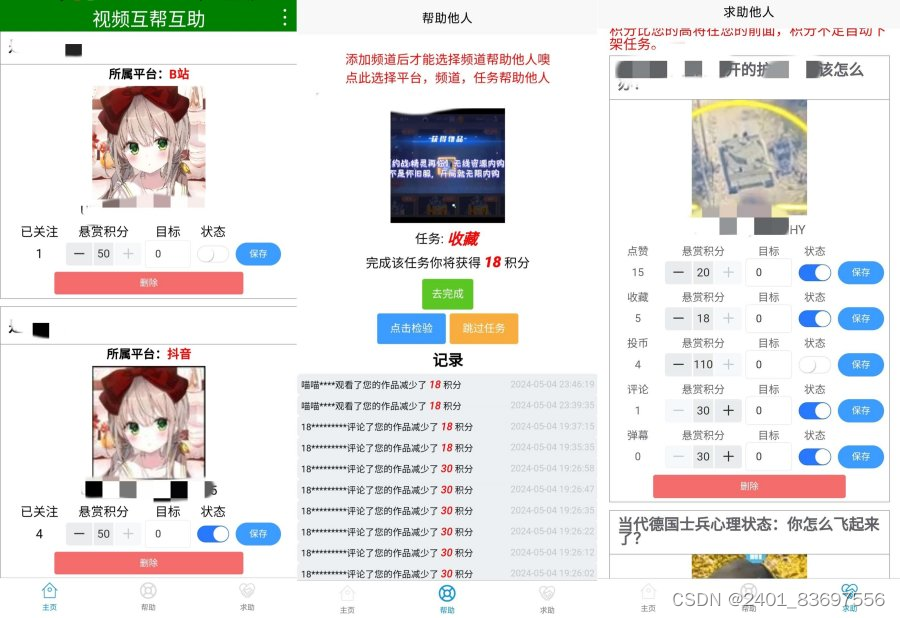
UP互助 帮助UP起号做视频 支持B站和抖音
【软件名字】:UP互助 【软件版本】:1.0 【软件大小】:17.5MB 【软件平台】:安卓 【测试机型】:小米9 1.随便登个邮箱,添加自己平台的频道,然后就可以帮助别人,添加频道后在添加…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...
