Eigen求解线性方程组
1、线性方程组的应用
线性方程组可以用来解决各种涉及线性关系的问题。以下是一些通常可以用线性方程组来解决的问题:
在实际工程和科学计算中,求解多项式方程的根有着广泛的应用。
在控制系统的设计中,我们经常需要求解特征方程的根来分析系统的稳定性;
在图像处理和模式识别中,多项式方程的根可以用来寻找图像的特征点;
在金融工程和风险管理中,多项式方程的根可以用来对数据进行拟合和预测。
-
工程问题:工程领域中存在大量的线性关系问题,例如:
- 结构力学:求解结构物体系的平衡状态。
- 电路分析:计算电路中的电流、电压等。
- 控制系统:建立控制系统的数学模型,进行分析和设计。
-
物理问题:物理学中很多问题都可以归结为线性方程组,例如:
- 运动学和动力学:描述物体在运动过程中的位移、速度、加速度等。
- 电磁学:描述电场、磁场的分布和相互作用。
- 热传导:描述热量在物体内部传递和分布的过程。
-
优化问题:很多优化问题可以转化为线性方程组求解的问题,例如:
- 线性规划:通过线性方程组求解目标函数的最优值。
- 最小二乘法:拟合数据点到一个线性函数或者多项式,使得残差平方和最小化。
-
数据分析:数据分析中经常需要拟合数据、估计参数等,这些问题通常可以转化为线性方程组的形式来求解。
-
金融领域:金融领域中的风险评估、资产定价等问题也可以用线性方程组来描述和求解。
-
机器学习和模式识别:很多机器学习算法和模式识别方法涉及到解决线性方程组,例如:
- 线性回归:建立线性模型来预测或拟合数据。
- 支持向量机:求解超平面来进行分类。
2、Eigen求解线性方程组
Eigen提供了多种方法来求解线性方程组,具体取决于方程组的特性、稀疏程度以及性能需求。以下是Eigen中常用的一些线性方程组求解方法:
-
直接解法:
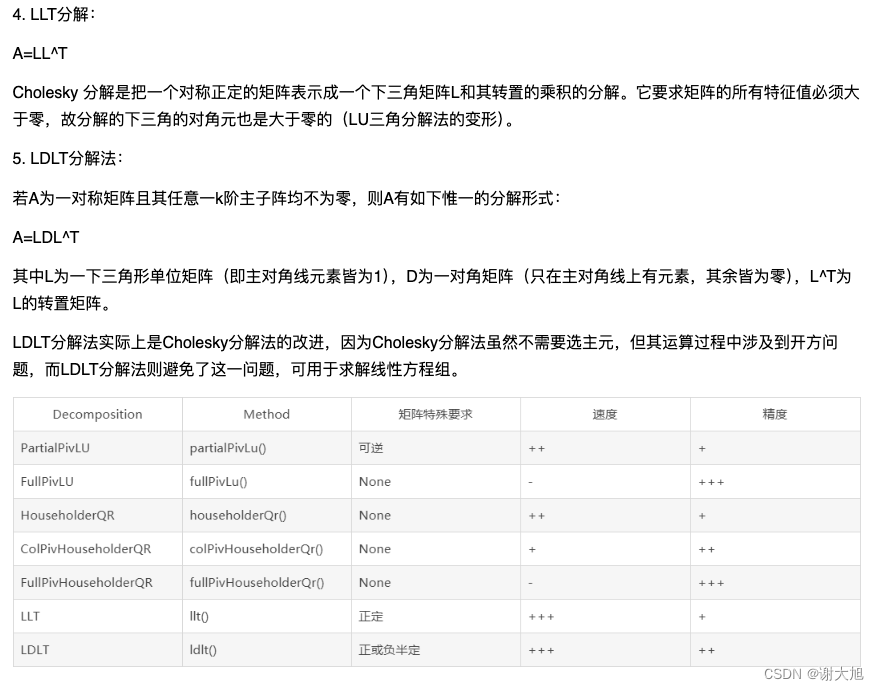
- LU分解:通过LU分解(或者部分选主元LU分解)来求解稠密矩阵的线性方程组。
- LLT分解:用于对称正定矩阵的Cholesky分解。
- LDLT分解:用于对称矩阵的LDLT分解。
-
迭代法:
- Jacobi迭代法
- Gauss-Seidel迭代法
- Successive Over-Relaxation (SOR)迭代法
- Conjugate Gradient (CG)方法:用于对称正定矩阵的迭代法。
- BiCGSTAB方法:用于一般非对称矩阵的迭代法。
- GMRES方法:广义最小残差法,用于非对称矩阵的迭代法。
-
QR分解:通过QR分解求解线性方程组,例如使用Householder QR分解或者ColPivHouseholderQR分解。
-
SVD分解:使用奇异值分解(Singular Value Decomposition)来求解最小二乘问题或者解决非方阵的线性方程组。
-
稀疏矩阵求解:对于稀疏矩阵,Eigen也提供了一些特定的求解器,如BiCGSTAB、SparseLU等。
每种方法都有其适用范围和性能特点,选择合适的方法取决于线性方程组的特性以及求解的需求(例如精度、速度、稀疏性等)。Eigen提供了丰富的线性方程组求解功能,可以根据具体情况选择最合适的方法。
2、线性方程组的构造
这个需要另外写一篇博客总结下什么问题可以用线性方程组来建模。下一篇就来学习下Eigen在orb-slam2中的应用。
3、参考文献

eigen稀疏矩阵求逆 - 百度文库 (baidu.com)
相关文章:

Eigen求解线性方程组
1、线性方程组的应用 线性方程组可以用来解决各种涉及线性关系的问题。以下是一些通常可以用线性方程组来解决的问题: 在实际工程和科学计算中,求解多项式方程的根有着广泛的应用。 在控制系统的设计中,我们经常需要求解特征方程的根来分析…...

7、Java基本数据类型的使用细节探讨(超详细版本)
Java基本数据类型的使用细节探讨 一、整数类型二、浮点数三、字符型四、布尔型 我觉得基本数据类型大家学计算机的应该都懂,但是韩顺平老师讲的基本类型的使用细节我觉得有必要记录一下,重新学的时候才发现有了新的感悟! 一、整数类型 使用细…...
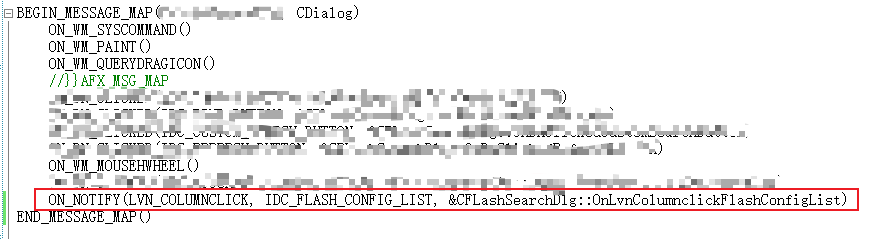
MFC实现点击列表头进行排序
MFC实现点击列表头排序 1、添加消息处理函数 在列表窗口右键,类向导。选择 IDC_LIST1(我的列表控件的ID),消息选择LVN_COLUMNCLICK。 2、消息映射如下 然后会在 cpp 文件中生成以下函数 void CFLashSearchDlg::OnLvnColumnclic…...
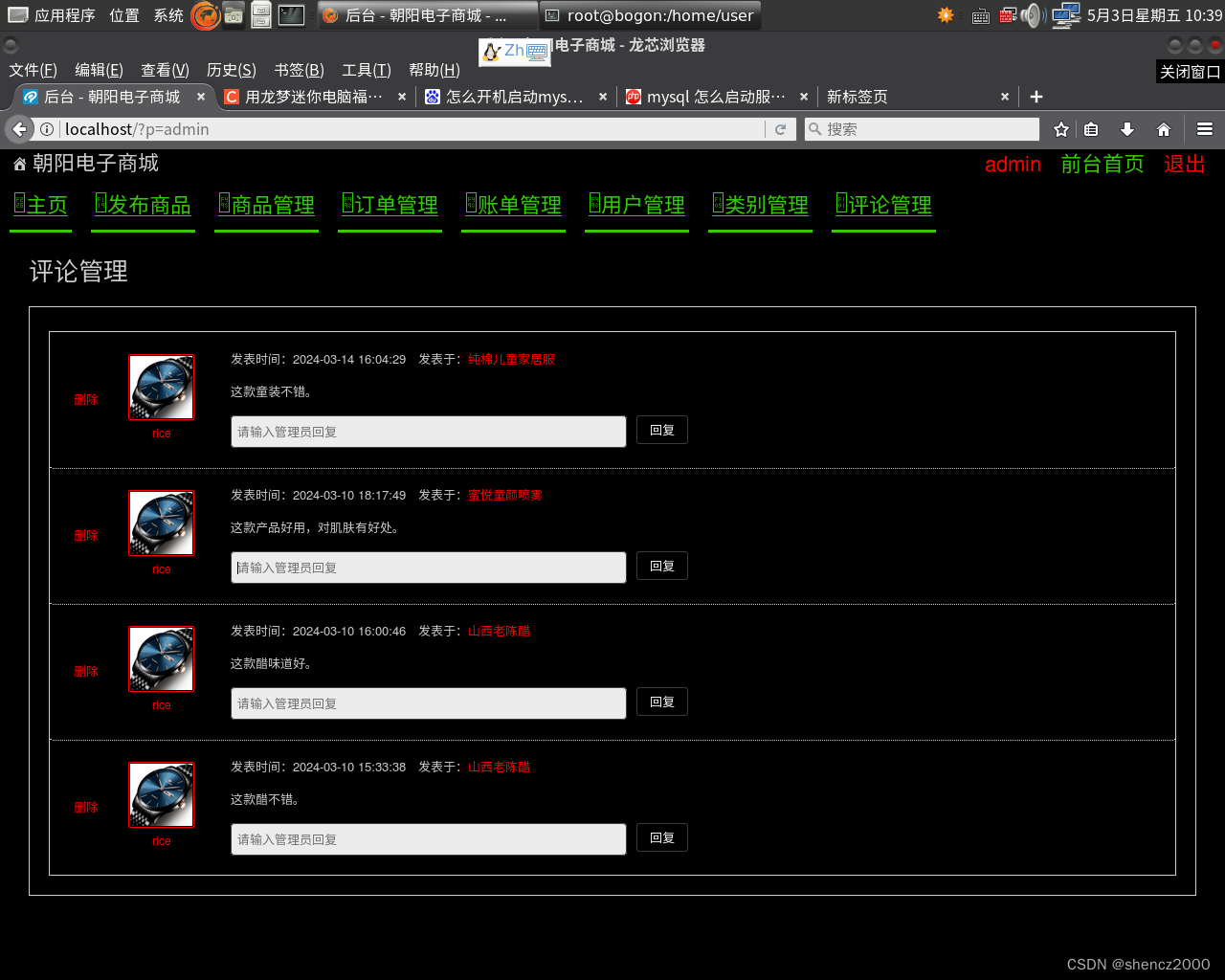
用龙梦迷你电脑福珑2.0做web服务器
用龙梦迷你电脑福珑2.0上做web服务器是可行的。已将一个网站源码放到该电脑,在局域网里可以访问网站网页。另外通过在同一局域网内的一台windows10电脑上安装花生壳软件,也可以在外网访问该内网服务器网站网页。该电脑的操作系统属于LAMP。在该电脑上安装…...

秋招后端开发面试题 - JVM类加载机制
目录 JVM类加载机制前言面试题能说一下类的生命周期吗?类加载的过程知道吗?类加载器有哪些?什么是双亲委派机制?为什么要用双亲委派机制?如何破坏双亲委派机制?如何判断一个类是无用的类? JVM类…...

OceanBase 分布式数据库【信创/国产化】- OceanBase 配置项和系统变量概述
本心、输入输出、结果 文章目录 OceanBase 分布式数据库【信创/国产化】- OceanBase 配置项和系统变量概述前言OceanBase 数据更新架构OceanBase 配置项和系统变量概述配置项配置项分类配置项查询系统变量系统变量分类系统变量查询配置项与系统变量的区分OceanBase 分布式数据库…...

单单单单单の刁队列
在数据结构的学习中,队列是一种常用的线性数据结构,它遵循先进先出(FIFO)的原则。而单调队列是队列的一种变体,它在特定条件下保证了队列中的元素具有某种单调性质,例如单调递增或单调递减。单调队列在处理…...
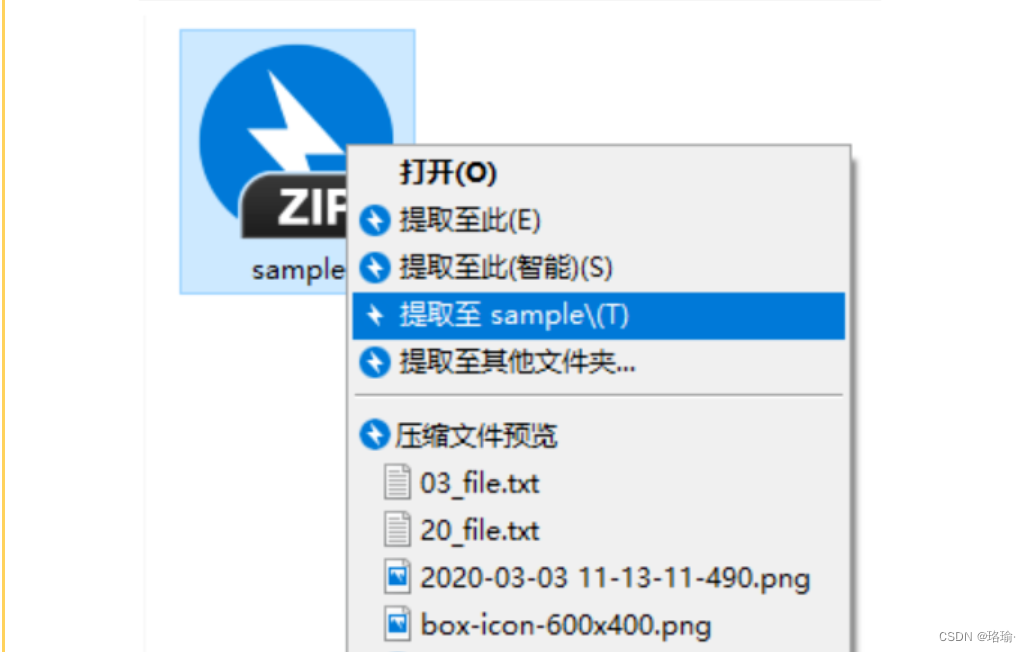
电脑windows系统压缩解压软件-Bandizip
一、软件功能 Bandizip是一款功能强大的压缩和解压缩软件,具有快速拖放、高速压缩、多核心支持以及广泛的文件格式支持等特点。 Bandizip软件的功能主要包括: 1. 支持多种文件格式 Bandizip可以处理多种压缩文件格式,包括ZIP, 7Z, RAR, A…...
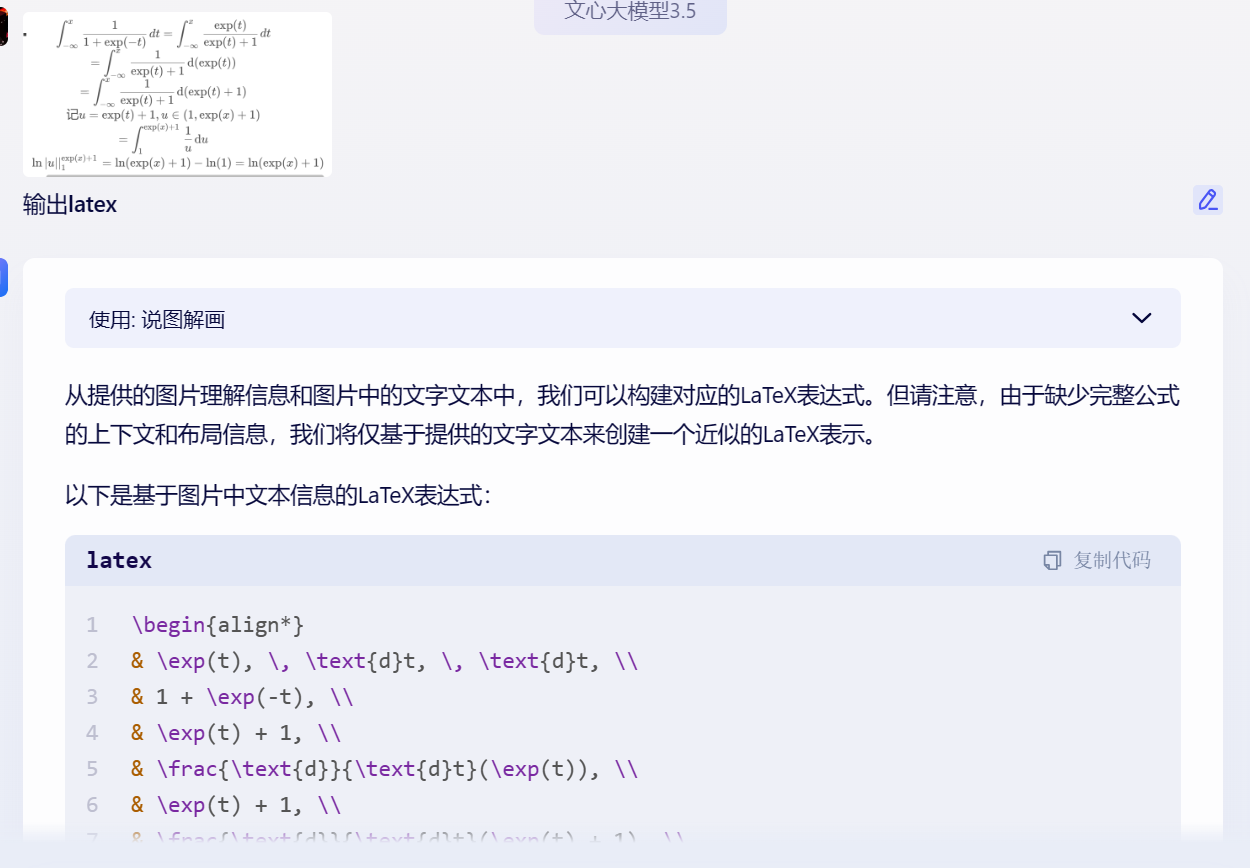
图片公式识别@文档公式识别@表格识别@在线和离线OCR工具
文章目录 abstract普通文字识别本地软件识别公式扩展插件下载小结 在线识别网站/API👺Quicker整合(推荐)可视化编辑和识别公式其他多模态大模型识别图片中的公式排版 开源模型 abstract 本文介绍免费图片文本识别(OCR)工具,包括普通文字识别,公式识别,甚至是手写公…...
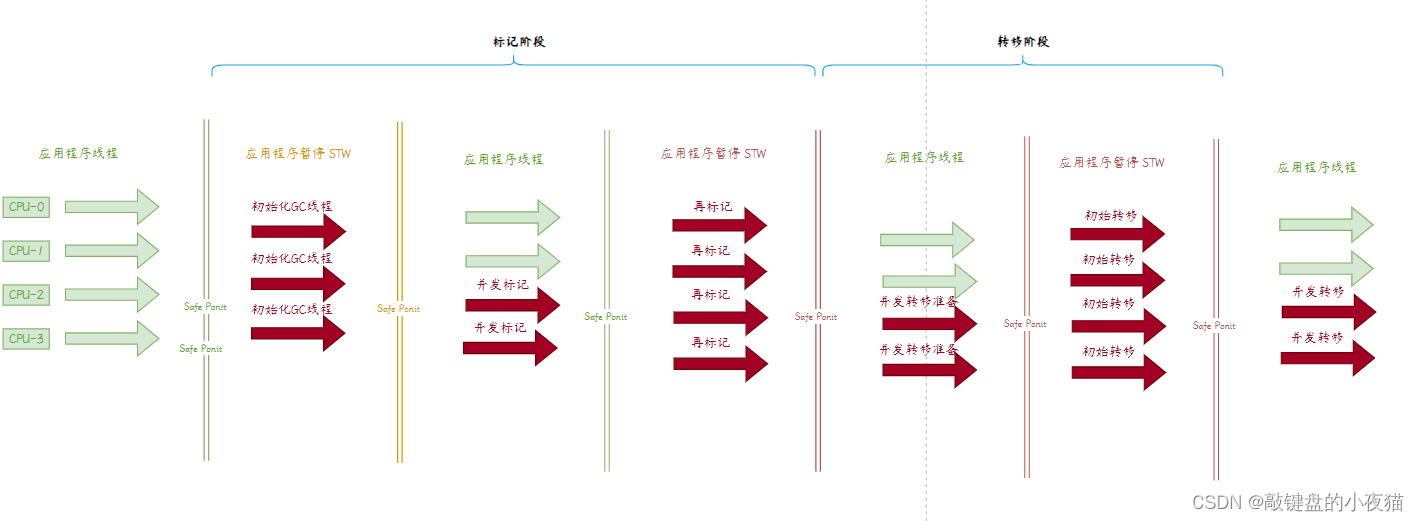
Java高阶私房菜:JVM分代收集算法介绍和各垃圾收集器原理分解
目录 什么是分代收集算法 GC的分类和专业术语 什么是垃圾收集器 垃圾收集器的分类及组合 编辑 应关注的核心指标 Serial和ParNew收集器原理 Serial收集器 ParNew收集器 Parallel和CMS收集器原理 Parallel 收集器 CMS收集器 新一代垃圾收集器G1和ZGC G1垃圾收集器…...

为什么IB损失要在100epochs后再用?
在给定的代码中,参数start_ib_epoch用于控制从第几轮开始使用IB(Instance-Balanced)损失函数进行训练。具体来说,如果start_ib_epoch的值大于等于100,那么在训练的前100轮中将使用普通的交叉熵损失函数(CE&…...
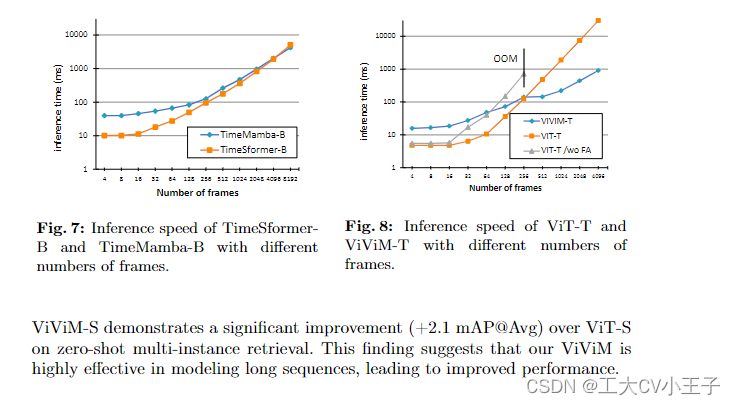
《Video Mamba Suite》论文笔记(4)Mamba在时空建模中的作用
原文翻译 4.4 Mamba for Spatial-Temporal Modeling Tasks and datasets.最后,我们评估了 Mamba 的时空建模能力。与之前的小节类似,我们在 Epic-Kitchens-100 数据集 [13] 上评估模型在zero-shot多实例检索中的性能。 Baseline and competitor.ViViT…...
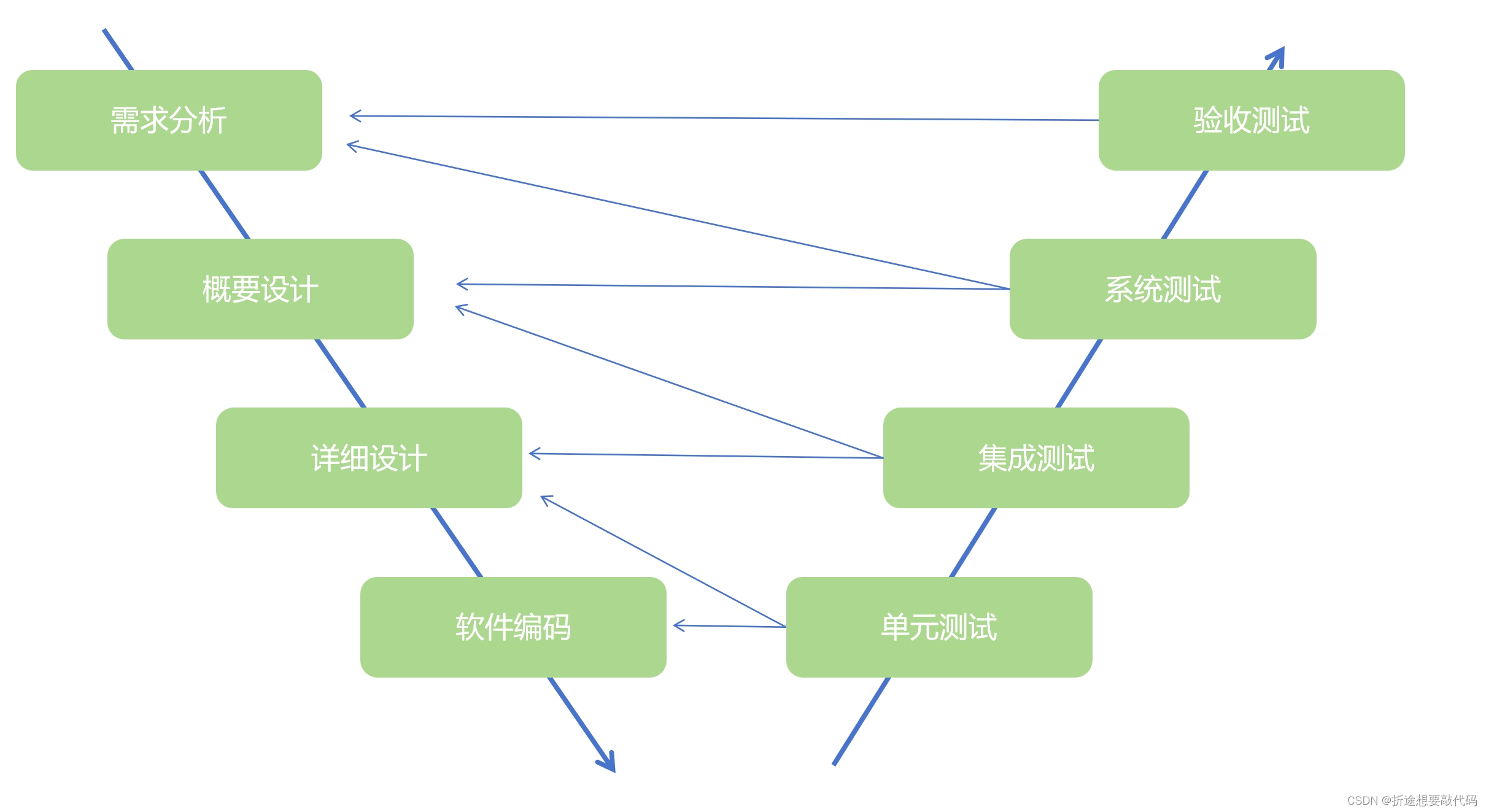
【备战软考(嵌入式系统设计师)】10 - 软件工程基础
这一部分的内容是概念比较多,不要理解,去感受。 涉及的知识点是嵌入式系统开发和维护的部分,也就是和管理相关的,而不是具体如何进行嵌入式系统开发的细节。 系统开发生命周期 按照顺序有下面几个阶段,我们主要要记…...

随手笔记-GNN(朴素图神经网络)
自己看代码随手写的一点备忘录,自己看的,不喜勿喷 GNN (《------ 代码) 刚开始我还在怀疑为什么没有加weigth bias,已经为什么权重才两个,原来是对node_feats进行的network的传播,而且自己内部直接进行了。 下面是一…...

C 语言指针怎么理解?
在今天的学习中,我注意到有位学员似乎对 C 语言指针的理解有些困惑。为了帮助大家更好地理解,我来举个例子。 C 语言指针就好比 Windows 桌面上常见的快捷方式。快捷方式可以指向某个游戏,这就是普通指针;它也可以指向另一个快捷…...

HTTP协议:通信机制、特点及实践应用
目录 前言 1. 运行机制 2. 通信方式 3. 主要特点 4. 统一资源标识符(URL) 5. HTTP报文 6. HTTP请求 7. HTTP响应 8. 实体 9. 持续连接 结语 前言 HTTP(Hypertext Transfer Protocol)是互联网上应用最广泛的一种协议&a…...

Leetcode—289. 生命游戏【中等】
2024每日刷题(126) Leetcode—289. 生命游戏 算法思想 实现代码 class Solution { public:void gameOfLife(vector<vector<int>>& board) {int rows board.size();int cols board[0].size();int neighbors[3] {0, 1, -1};vector<…...
系统运维(虚拟化)
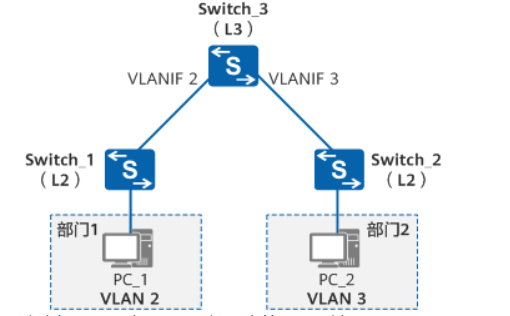
1.VLAN VLAN(Virtual Local Area Network)即虚拟局域网,是将一个物理的LAN在逻辑上划分成多个广播域的通信技术。 每个VLAN是一个广播域,VLAN内的主机间可以直接通信,而VLAN间则不能直接互通。这样,广播报…...
Linux域名解析
1.hosts:windows c盘下面 Linux: /etc/hosts 作用:实现名字解析,主要为本地主机名、集群节点提供快速解析。平面式结构,集中式数据库。 缺点:不便于查询更新 2.DNS:域名系统 作用:实现名字解析(分层性,层次性) FQDN:完全合格域名/全称域…...

树形结构和列表的区别
树形结构和列表在数据组织、表示方式以及应用场景等方面存在明显的区别。 首先,树形结构是一种非线性的数据结构,表现为层次的嵌套结构。每个节点可以有多个子节点,这些子节点又可以有自己的子节点,形成一个层次分明的结构。这种一…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...
