2024.5.2 —— LeetCode 高频题复盘
目录
- 151. 反转字符串中的单词
- 129. 求根节点到叶节点数字之和
- 104. 二叉树的最大深度
- 101. 对称二叉树
- 110. 平衡二叉树
- 144. 二叉树的前序遍历
- 543. 二叉树的直径
- 48. 旋转图像
- 98. 验证二叉搜索树
- 39. 组合总和
151. 反转字符串中的单词
题目链接
class Solution:def reverseWords(self, s: str) -> str:ls=s.strip().split()ls.reverse()res=" ".join(ls)return res
129. 求根节点到叶节点数字之和
题目链接
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def helper(self,root,i):if not root:return 0temp=i*10+root.valif not root.left and not root.right:return tempreturn self.helper(root.left,temp)+self.helper(root.right,temp)def sumNumbers(self, root: Optional[TreeNode]) -> int:return self.helper(root,0)
104. 二叉树的最大深度
题目链接
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def maxDepth(self, root: Optional[TreeNode]) -> int:if not root:return 0leftHight=self.maxDepth(root.left)rightHigh=self.maxDepth(root.right)return max(leftHight,rightHigh)+1
101. 对称二叉树
题目链接
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def isSymmetric(self, root: Optional[TreeNode]) -> bool:def judge(left,right):if not left and not right:return Trueelif not left or not right:return Falseelif left.val!=right.val:return Falseelse:return judge(left.left,right.right) and judge(left.right,right.left)if not root:return Truereturn judge(root.left,root.right)
110. 平衡二叉树
题目链接
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def isBalanced(self, root: Optional[TreeNode]) -> bool:# 二叉树的最大深度def height(root):if not root:return 0return max(height(root.left),height(root.right))+1if not root:return Truereturn abs(height(root.left)-height(root.right))<=1 and self.isBalanced(root.left) and self.isBalanced(root.right)
144. 二叉树的前序遍历
题目链接
递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:lis=[]def traversal(root):if not root:returnlis.append(root.val)traversal(root.left)traversal(root.right)traversal(root)return lis
非递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:white,gray=0,1stack=[(white,root)]res=[]while stack:color,node=stack.pop()if node is None:continueif color==white:stack.append((white,node.right))stack.append((white,node.left))stack.append((gray,node))else:res.append(node.val)return res
543. 二叉树的直径
题目链接
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:# 一条路径的长度为该路径经过的节点数减一,# 所以求直径(即求路径长度的最大值)等效于求路径经过节点数的最大值减一self.max=0def depth(root):if not root:return 0left=depth(root.left)right=depth(root.right)self.max=max(self.max,left+right+1)return max(left,right)+1depth(root)return self.max-1
48. 旋转图像
题目链接
class Solution:def rotate(self, matrix: List[List[int]]) -> None:"""Do not return anything, modify matrix in-place instead."""# 用翻转代替旋转# 先水平翻转再主对角线翻转即可得到将图像顺时针旋转90度的图像n=len(matrix)# 水平翻转for i in range(n//2):for j in range(n):matrix[i][j],matrix[n-1-i][j]=matrix[n-1-i][j],matrix[i][j]# 主对角线翻转for i in range(n):for j in range(i):matrix[i][j],matrix[j][i]=matrix[j][i],matrix[i][j]
98. 验证二叉搜索树
题目链接
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def isValidBST(self, root: Optional[TreeNode]) -> bool:# 中序遍历:左中右self.pre=Nonedef dfs(root):if not root:return Trueleft=dfs(root.left)if self.pre and self.pre.val>=root.val:return Falseself.pre=rootright=dfs(root.right)return left and rightreturn dfs(root)
39. 组合总和
题目链接
class Solution:def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:path=[]res=[]def backtracking(candidates,s,target,startIndex):if s>target: # 要剪枝必须排序returnif s==target:res.append(path[:])returnfor i in range(startIndex,len(candidates)):s+=candidates[i]path.append(candidates[i])backtracking(candidates,s,target,i) # 下一层i依然可以取到s-=candidates[i]path.pop()candidates.sort()backtracking(candidates,0,target,0)return res
相关文章:

2024.5.2 —— LeetCode 高频题复盘
目录 151. 反转字符串中的单词129. 求根节点到叶节点数字之和104. 二叉树的最大深度101. 对称二叉树110. 平衡二叉树144. 二叉树的前序遍历543. 二叉树的直径48. 旋转图像98. 验证二叉搜索树39. 组合总和 151. 反转字符串中的单词 题目链接 class Solution:def reverseWords(s…...

ThreeJS:光线投射与3D场景交互
光线投射Raycaster 光线投射详细介绍可参考:https://en.wikipedia.org/wiki/Ray_casting, ThreeJS中,提供了Raycaster类,用于进行鼠标拾取,即:当三维场景中鼠标移动时,利用光线投射,…...
docker挂载数据卷-以nginx为例
目录 一、什么是数据卷 二、数据卷的作用 三、如何挂载数据卷 1、创建nginx容器挂载数据卷 2、查看数据卷 3、查看数据卷详情 4、尝试在宿主机修改数据卷 5、查看容器内对应的数据卷目录 6、 访问nginx查看效果 一、什么是数据卷 挂载数据卷本质上就是实…...

Docker-compose部署Fastapi项目
Docker-compose部署Fastapi、postgres、Redis、Nginx) 之前有写过使用容器部署的方式,这次尝试使用Docker-compose试一次大胆的尝试 使用容器的方式部署只是掌握这项技能的基础,在使用Docker-compose的过程中会有些稍许的不同。毕竟踩过的坑才算是跨过去…...
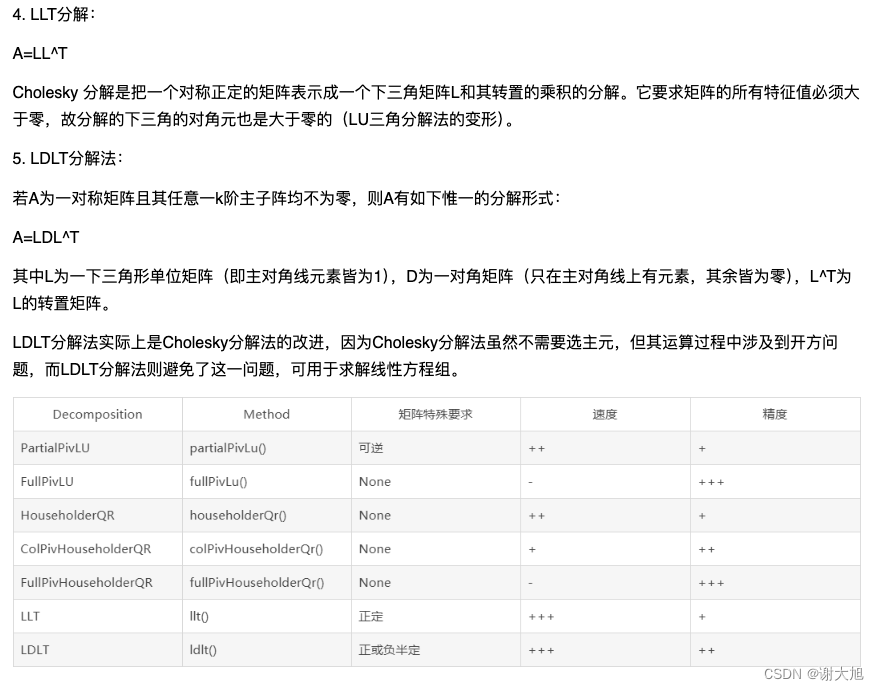
Eigen求解线性方程组
1、线性方程组的应用 线性方程组可以用来解决各种涉及线性关系的问题。以下是一些通常可以用线性方程组来解决的问题: 在实际工程和科学计算中,求解多项式方程的根有着广泛的应用。 在控制系统的设计中,我们经常需要求解特征方程的根来分析…...

7、Java基本数据类型的使用细节探讨(超详细版本)
Java基本数据类型的使用细节探讨 一、整数类型二、浮点数三、字符型四、布尔型 我觉得基本数据类型大家学计算机的应该都懂,但是韩顺平老师讲的基本类型的使用细节我觉得有必要记录一下,重新学的时候才发现有了新的感悟! 一、整数类型 使用细…...
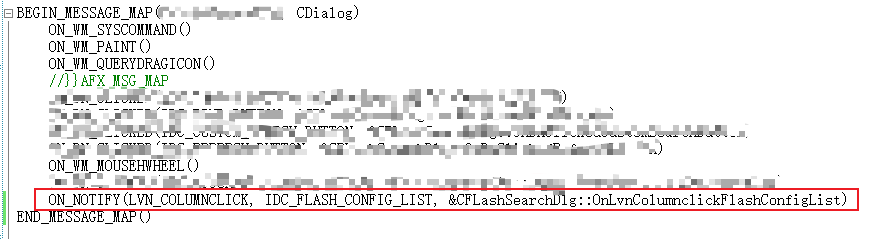
MFC实现点击列表头进行排序
MFC实现点击列表头排序 1、添加消息处理函数 在列表窗口右键,类向导。选择 IDC_LIST1(我的列表控件的ID),消息选择LVN_COLUMNCLICK。 2、消息映射如下 然后会在 cpp 文件中生成以下函数 void CFLashSearchDlg::OnLvnColumnclic…...
用龙梦迷你电脑福珑2.0做web服务器
用龙梦迷你电脑福珑2.0上做web服务器是可行的。已将一个网站源码放到该电脑,在局域网里可以访问网站网页。另外通过在同一局域网内的一台windows10电脑上安装花生壳软件,也可以在外网访问该内网服务器网站网页。该电脑的操作系统属于LAMP。在该电脑上安装…...

秋招后端开发面试题 - JVM类加载机制
目录 JVM类加载机制前言面试题能说一下类的生命周期吗?类加载的过程知道吗?类加载器有哪些?什么是双亲委派机制?为什么要用双亲委派机制?如何破坏双亲委派机制?如何判断一个类是无用的类? JVM类…...

OceanBase 分布式数据库【信创/国产化】- OceanBase 配置项和系统变量概述
本心、输入输出、结果 文章目录 OceanBase 分布式数据库【信创/国产化】- OceanBase 配置项和系统变量概述前言OceanBase 数据更新架构OceanBase 配置项和系统变量概述配置项配置项分类配置项查询系统变量系统变量分类系统变量查询配置项与系统变量的区分OceanBase 分布式数据库…...

单单单单单の刁队列
在数据结构的学习中,队列是一种常用的线性数据结构,它遵循先进先出(FIFO)的原则。而单调队列是队列的一种变体,它在特定条件下保证了队列中的元素具有某种单调性质,例如单调递增或单调递减。单调队列在处理…...
电脑windows系统压缩解压软件-Bandizip
一、软件功能 Bandizip是一款功能强大的压缩和解压缩软件,具有快速拖放、高速压缩、多核心支持以及广泛的文件格式支持等特点。 Bandizip软件的功能主要包括: 1. 支持多种文件格式 Bandizip可以处理多种压缩文件格式,包括ZIP, 7Z, RAR, A…...
图片公式识别@文档公式识别@表格识别@在线和离线OCR工具
文章目录 abstract普通文字识别本地软件识别公式扩展插件下载小结 在线识别网站/API👺Quicker整合(推荐)可视化编辑和识别公式其他多模态大模型识别图片中的公式排版 开源模型 abstract 本文介绍免费图片文本识别(OCR)工具,包括普通文字识别,公式识别,甚至是手写公…...
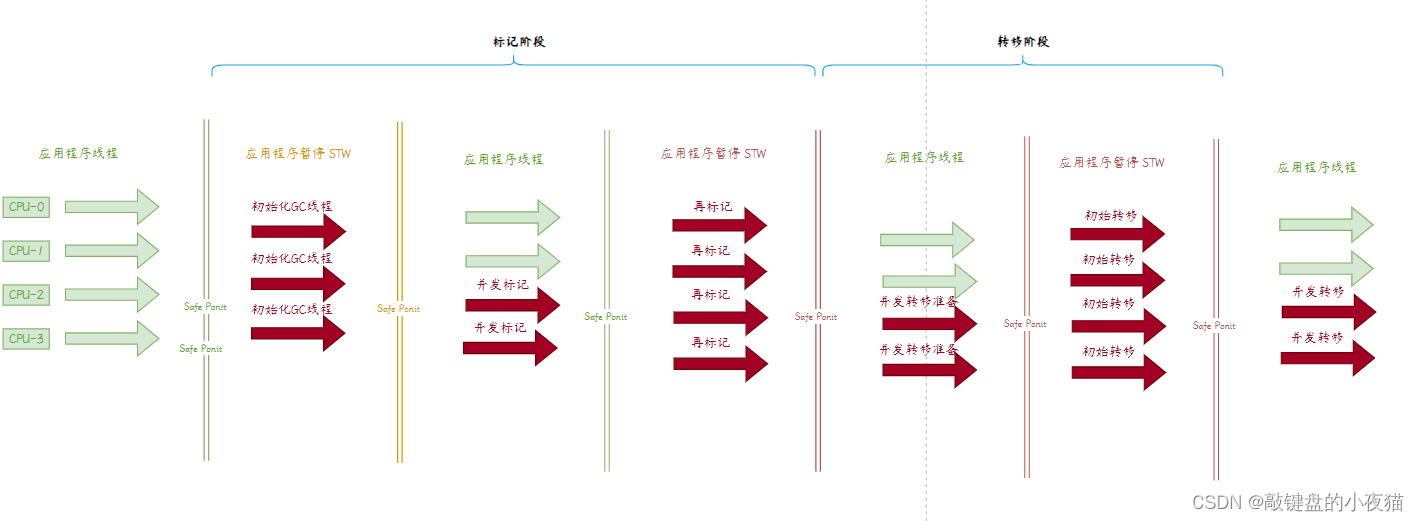
Java高阶私房菜:JVM分代收集算法介绍和各垃圾收集器原理分解
目录 什么是分代收集算法 GC的分类和专业术语 什么是垃圾收集器 垃圾收集器的分类及组合 编辑 应关注的核心指标 Serial和ParNew收集器原理 Serial收集器 ParNew收集器 Parallel和CMS收集器原理 Parallel 收集器 CMS收集器 新一代垃圾收集器G1和ZGC G1垃圾收集器…...

为什么IB损失要在100epochs后再用?
在给定的代码中,参数start_ib_epoch用于控制从第几轮开始使用IB(Instance-Balanced)损失函数进行训练。具体来说,如果start_ib_epoch的值大于等于100,那么在训练的前100轮中将使用普通的交叉熵损失函数(CE&…...
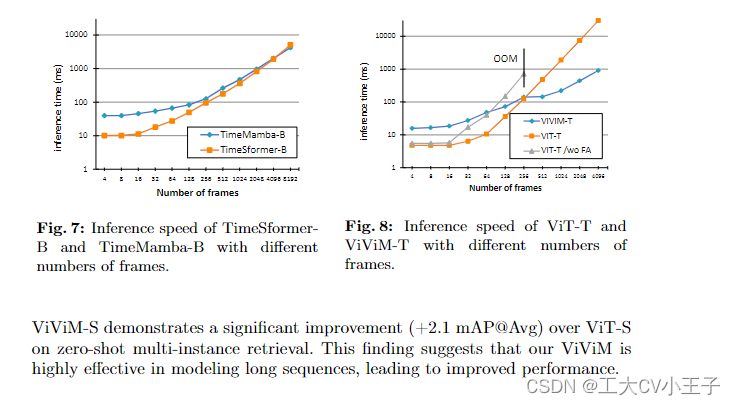
《Video Mamba Suite》论文笔记(4)Mamba在时空建模中的作用
原文翻译 4.4 Mamba for Spatial-Temporal Modeling Tasks and datasets.最后,我们评估了 Mamba 的时空建模能力。与之前的小节类似,我们在 Epic-Kitchens-100 数据集 [13] 上评估模型在zero-shot多实例检索中的性能。 Baseline and competitor.ViViT…...
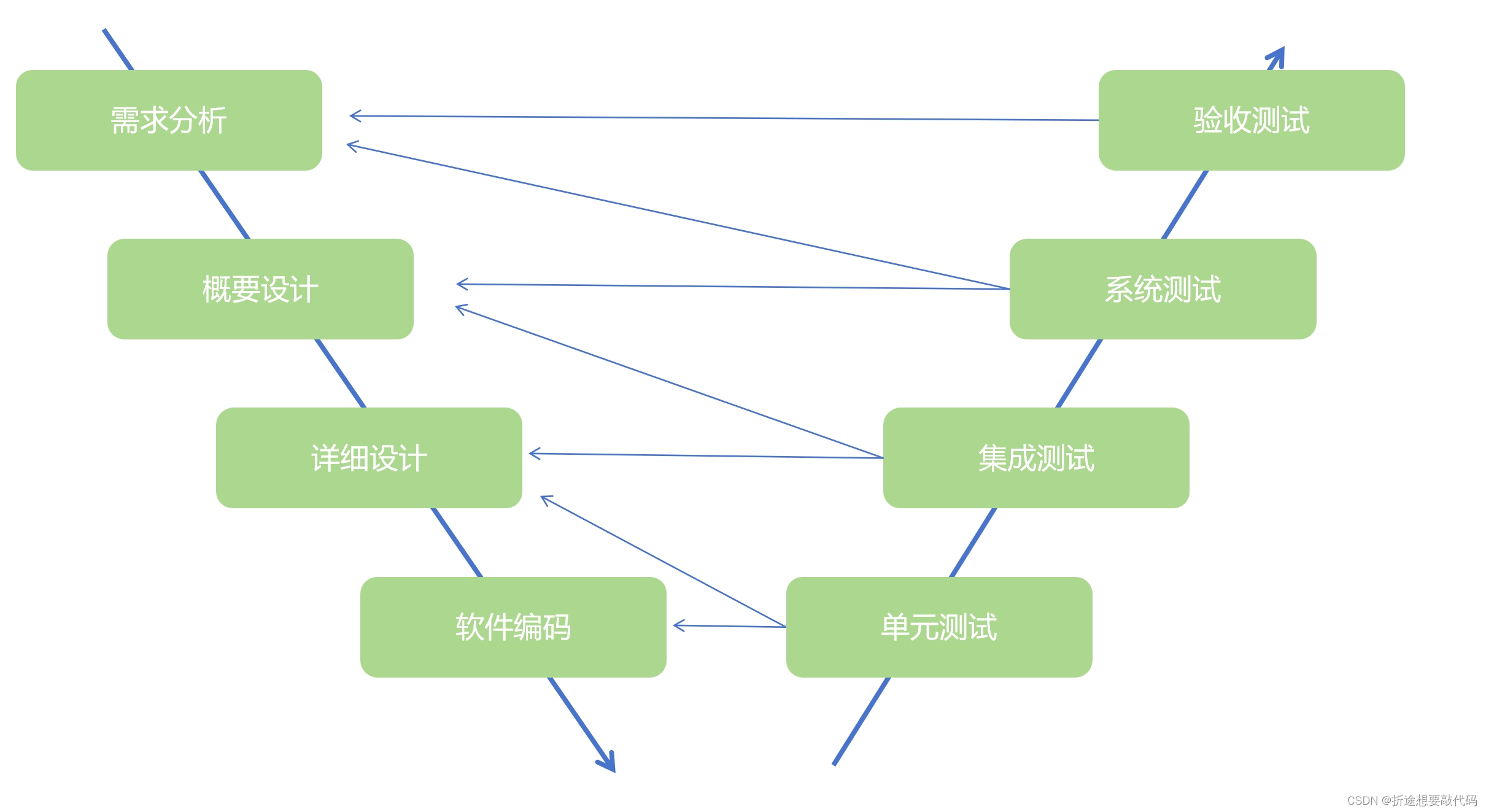
【备战软考(嵌入式系统设计师)】10 - 软件工程基础
这一部分的内容是概念比较多,不要理解,去感受。 涉及的知识点是嵌入式系统开发和维护的部分,也就是和管理相关的,而不是具体如何进行嵌入式系统开发的细节。 系统开发生命周期 按照顺序有下面几个阶段,我们主要要记…...

随手笔记-GNN(朴素图神经网络)
自己看代码随手写的一点备忘录,自己看的,不喜勿喷 GNN (《------ 代码) 刚开始我还在怀疑为什么没有加weigth bias,已经为什么权重才两个,原来是对node_feats进行的network的传播,而且自己内部直接进行了。 下面是一…...

C 语言指针怎么理解?
在今天的学习中,我注意到有位学员似乎对 C 语言指针的理解有些困惑。为了帮助大家更好地理解,我来举个例子。 C 语言指针就好比 Windows 桌面上常见的快捷方式。快捷方式可以指向某个游戏,这就是普通指针;它也可以指向另一个快捷…...

HTTP协议:通信机制、特点及实践应用
目录 前言 1. 运行机制 2. 通信方式 3. 主要特点 4. 统一资源标识符(URL) 5. HTTP报文 6. HTTP请求 7. HTTP响应 8. 实体 9. 持续连接 结语 前言 HTTP(Hypertext Transfer Protocol)是互联网上应用最广泛的一种协议&a…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...
