95、动态规划-编辑距离
递归暴力解法
递归方法的基本思想是考虑最后一个字符的操作,然后根据这些操作递归处理子问题。
递归函数定义:定义一个递归函数 minDistance(i, j),表示将 word1 的前 i 个字符转换成 word2 的前 j 个字符所需的最小操作数。
递归终止条件:
- 如果
i == 0,意味着word1为空,此时将word1转换成word2的前j个字符就需要j次插入操作。 - 如果
j == 0,意味着word2为空,此时将word1的前i个字符转换成空字符串需要i次删除操作。
递归转移方程:
- 如果
word1[i-1] == word2[j-1],则当前两个字符相等,不需要操作,所以minDistance(i, j) = minDistance(i-1, j-1)。 - 如果不相等,则可以进行插入、删除或替换操作,转移方程为:
- 插入:
minDistance(i, j) = minDistance(i, j-1) + 1 - 删除:
minDistance(i, j) = minDistance(i-1, j) + 1 - 替换:
minDistance(i, j) = minDistance(i-1, j-1) + 1
- 插入:
- 取三者的最小值。
代码如下:
public class Solution {// 主方法,用于外部调用,传入两个字符串public int minDistance(String word1, String word2) {// 调用递归助手函数,初始化i和j为字符串的长度,从字符串尾部开始比较return minDistanceHelper(word1, word2, word1.length(), word2.length());}// 递归助手函数,用于计算两个字符串的最小编辑距离private int minDistanceHelper(String word1, String word2, int m, int n) {// 如果第一个字符串为空,则转换的代价是第二个字符串的长度(即插入n次)if (m == 0) return n;// 如果第二个字符串为空,则转换的代价是第一个字符串的长度(即删除m次)if (n == 0) return m;// 如果两个字符串的当前字符相等,则不需要操作,递归考虑前一个字符if (word1.charAt(m - 1) == word2.charAt(n - 1)) {return minDistanceHelper(word1, word2, m - 1, n - 1);}// 计算插入操作的代价:将word2的第n个字符插入到word1的末尾,然后继续处理剩余的字符串int insert = minDistanceHelper(word1, word2, m, n - 1) + 1;// 计算删除操作的代价:删除word1的第m个字符,然后继续处理剩余的字符串int delete = minDistanceHelper(word1, word2, m - 1, n) + 1;// 计算替换操作的代价:将word1的第m个字符替换为word2的第n个字符,然后继续处理剩余的字符串int replace = minDistanceHelper(word1, word2, m - 1, n - 1) + 1;// 返回三种操作中的最小值,即为到当前位置为止的最小编辑距离return Math.min(Math.min(insert, delete), replace);}
}
但是重复计算效率很慢,改成动态规划:
动态规划方法
动态规划方法的核心思想是使用一个二维数组 dp 来存储中间结果,其中 dp[i][j] 表示将 word1 的前 i 个字符转换成 word2 的前 j 个字符所需的最小操作数。通过填充这个数组,我们可以逐步构建出从一个空字符串到完整 word2,再从完整 word1 到 word2 的转换路径。
初始化:
dp[0][j]:将空字符串转换为word2的前j个字符,需要j次插入操作。dp[i][0]:将word1的前i个字符转换为空字符串,需要i次删除操作。
状态转移方程:
- 如果
word1[i-1] == word2[j-1],则dp[i][j] = dp[i-1][j-1],因为最后一个字符已经匹配,不需要额外操作。 - 如果
word1[i-1] != word2[j-1],则可以从以下三个可能的操作中选择最小成本的:- 插入:
dp[i][j] = dp[i][j-1] + 1 - 删除:
dp[i][j] = dp[i-1][j] + 1 - 替换:
dp[i][j] = dp[i-1][j-1] + 1
- 插入:
代码如下:
public class Solution {public int minDistance(String word1, String word2) {int m = word1.length();int n = word2.length();int[][] dp = new int[m + 1][n + 1];// 初始化dp数组for (int i = 0; i <= m; i++) {dp[i][0] = i; // 从word1的i字符变为空字符串}for (int j = 0; j <= n; j++) {dp[0][j] = j; // 从空字符串变为word2的j字符}// 填充dp数组for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {if (word1.charAt(i - 1) == word2.charAt(j - 1)) {dp[i][j] = dp[i-1][j-1];} else {dp[i][j] = Math.min(Math.min(dp[i-1][j] + 1, dp[i][j-1] + 1), dp[i-1][j-1] + 1);}}}return dp[m][n];}
}
相关文章:

95、动态规划-编辑距离
递归暴力解法 递归方法的基本思想是考虑最后一个字符的操作,然后根据这些操作递归处理子问题。 递归函数定义:定义一个递归函数 minDistance(i, j),表示将 word1 的前 i 个字符转换成 word2 的前 j 个字符所需的最小操作数。 递归终止条件…...

linux调试
文章目录 1. 使用打印来调试1.1 重定向1.2 标准预定义宏1.3 日志代码 2. 内核异常2.1 内核打印2.1.1 打印级别2.1.2 跟踪异常2.1.3 动态打印2.1.4 RAM console 2.2 OOPS2.2.1 有源代码的情况2.2.2 没有源代码的情况 3 查看日志4 工具调试 1. 使用打印来调试 1.1 重定向 2>…...
【C++】string类的使用②(容量接口Capacity || 元素获取Element access)
🔥个人主页: Forcible Bug Maker 🔥专栏: STL || C 目录 前言🔥容量接口(Capacity)size和lengthcapacitymax_sizereserveresizeclearemptyshrink_to_fit 🔥元素获取(Ele…...
【漏洞复现】某小日子太阳能系统DataCube3审计
漏洞描述 某小日子太阳能系统DataCube3终端测量系统 多个漏洞利用方式 免责声明 技术文章仅供参考,任何个人和组织使用网络应当遵守宪法法律,遵守公共秩序,尊重社会公德,不得利用网络从事危害国家安全、荣誉和利益,未经授权请勿利用文章中的技术资料对任何计算机系统进…...

探索Java的未来
目录 一、云计算与大数据 二、人工智能与机器学习 三、物联网与边缘计算 四、安全性与性能优化 五、社区与生态 Java,作为一种广泛使用的编程语言,自其诞生以来就以其跨平台性、面向对象特性和丰富的库资源赢得了开发者的青睐。然而,随着…...
Web3 ETF软件开发
开发Web3 ETF软件涉及到金融、法律和技术等多个领域的专业知识,因此存在以下技术难点,开发Web3 ETF软件是一项复杂的技术挑战,需要综合考虑各种因素。开发人员需要具备较强的技术能力和跨学科知识才能成功开发Web3 ETF软件。北京木奇移动技术…...

初始MySQL
初始化MySQL数据库通常涉及以下步骤: 下载并安装MySQL: 你可以从MySQL官方网站下载适合你的操作系统的MySQL安装包。安装时,遵循安装向导的步骤,通常包括选择安装位置、选择组件(例如MySQL服务器、MySQL Workbench等&a…...
)
STM32项目下载清单(不定时更新)
收集的一些资料,分享下载 电赛一等奖作品,老人健康监测智能手表(STM32F4主控) STM32数字示波器源码数字信号处理教程、配套实例基于stm32 nucleo_L476的智能灯(操作说明源码)基于STM32 NUCLEO板设计彩色LE…...

thinkphp5 配合阿里直播实现直播功能流程
要为你提供一个更详细的教程来结合ThinkPHP 5和阿里直播SDK实现直播功能,需要涵盖的内容相对较多。不过,我可以为你提供一个大致的、更详细的步骤指南,供你参考和扩展: 1. 准备工作 a. 注册阿里云账号 前往阿里云官网注册账号&…...

安卓手机APP开发__媒体3格式转换器__常见问题解答
安卓手机APP开发__媒体3格式转换器__常见问题解答 目录 1 为什么在示例的APP中我不能读取到本地的文件? 2 在一个特定的设备为什么导出失败? 3 媒体3格式转换器支持转码(或者是录制)远程的媒体吗? 4 媒体3格式转换…...
leetcode-有重复数字的全排列-98
题目要求 思路 1.同【没有重复项的全排列-97】这个题一样,都是递归的题,区别在于这个可能会包含重复的数字,因此,不能只是简单的通过两个值是否相等然后用标志位标记,而是新增了一个数组,这个数组专门用于…...
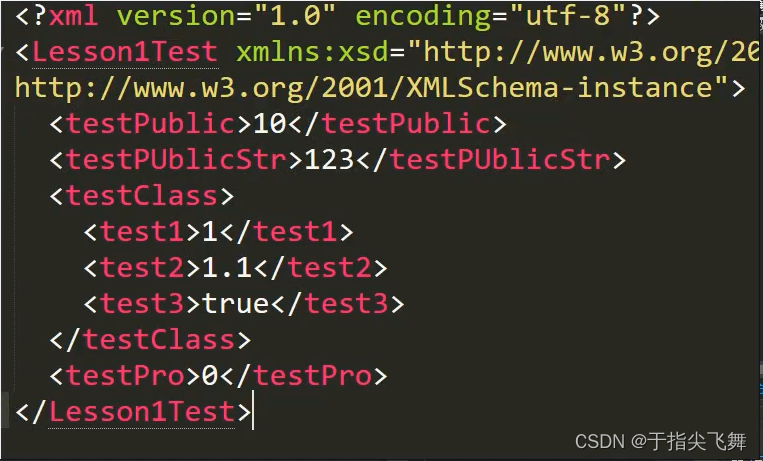
Unity数据持久化之XML
目录 数据持久化XML概述XML文件格式XML基本语法XML属性 C#读取存储XMLXML文件存放位置C#读取XML文件C#存储XML文件 实践小项目必备知识点XML序列化(不支持字典)XML反序列化IXmlSerializable接口让Dictionary支持序列化反序列化 数据持久化XML概述 什么是…...

Leetcode 226:翻转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。 思路:使用递归 //使用前序遍历翻转树public static TreeNode invertTree(TreeNode root){if(rootnull) return root;swap(root);invertTree(root.left);invertTree(root.rig…...

柯里化与无参装饰器
柯里化 柯里化的概念:柯里化(Currying)在Python中是一种编程技术,它将原本接受多个参数的函数转换为一系列接受单个参数的函数。这种方法以逻辑学家Haskell Curry的名字命名。 简而言之就是将一次函数调用变成先放入一个参数得到…...

Spring事务失效的场景
1. 事务方法执行期间出现了异常,但是并未指定rollbackFor: Spring默认只会在遇到error和RunTimeException时才会回滚。 public boolean rollbackon ( Throwable ex){return (ex instanceof RuntimeException || ex instanceof Error); } 2. 事务方法执行期间出现了…...

Python基础学习之datetime模块
在Python编程中,处理日期和时间是一个常见的需求。Python的datetime模块提供了丰富的类和方法,用于表示和操作日期、时间、时间间隔等。本文将详细介绍Python的datetime模块,并给出一些实用的示例。 1. datetime模块概览 datetime模块是Pyt…...

在AI大模型中全精度和半精度参数是什么意思?
环境: 大模型中 问题描述: 在AI大模型中全精度和半精度参数是什么意思? 解决方案: 在深度学习和高性能计算领域,"全精度"和"半精度"通常指的是模型中使用的数值表示的精度,具体涉…...

刷题记录2
文章目录 刷题记录21047.删除字符串中的所有相邻重复项150.逆波兰表达式求值239.滑动窗口最大值347.前k个高频元素144.二叉树前序遍历(145、94后序、中序)102.二叉树的层序遍历226.翻转二叉树101.对称二叉树104.二叉树的最大深度111.二叉树的最小深度222.完全二叉树的节点个数 …...

【配置】Docker搭建JSON在线解析网站
一个python朋友需要,顺便做一下笔记 正常用菜鸟的就够了,点下面 JSON在线解析 云服务器打开端口8787 连接上docker运行 docker run -id --name jsonhero -p 8787:8787 -e SESSION_SECRETabc123 henryclw/jsonhero-webhttp://ip:8787访问 Github&…...

2024.5.2 —— LeetCode 高频题复盘
目录 151. 反转字符串中的单词129. 求根节点到叶节点数字之和104. 二叉树的最大深度101. 对称二叉树110. 平衡二叉树144. 二叉树的前序遍历543. 二叉树的直径48. 旋转图像98. 验证二叉搜索树39. 组合总和 151. 反转字符串中的单词 题目链接 class Solution:def reverseWords(s…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...
