柯里化与无参装饰器
柯里化
柯里化的概念:柯里化(Currying)在Python中是一种编程技术,它将原本接受多个参数的函数转换为一系列接受单个参数的函数。这种方法以逻辑学家Haskell Curry的名字命名。
简而言之就是将一次函数调用变成先放入一个参数得到的中间函数对象,然后再对中间函数对象进行传参,这样可以将多参数函数变成多个单参数函数。
def add(x):def inner(y,z):return x+y+zreturn innerprint(add(1)(2,3))在第一个例子中,我们先将x传入得到一个带有x参数的函数对象,然后再对这个函数对象继续传入y,z两个参数,柯里化的程度是取决于我们的需要的,我们当然也可以将其分成三个函数,如下图
def add(x):def innner(y):def inner_1(z):return x+y+zreturn inner_1return innnerprint(add(1)(2)(3))现在,我们对柯里化有了一定了解,但我们该怎么把柯里化和装饰器关联在一起呢?
装饰器
你可以顾名思义,装饰器就是装饰函数用的,函数太单调?我们可以给它加一些功能让它尽可能丰满一些,为了丰富函数,有必要引入柯里化吗,我直接在函数里写不就行了?这就要考虑到代码侵入性问题了,我们将非业务代码(装饰代码)写在函数里,这就产生了业务与非业务代码的纠缠,这不利于后期代码的修改,何况,如果我想为多个函数进行装饰,难道我要一个一个copy过去?这显然不切实际,所以我们运用了函数的思想,把装饰代码封装到一个函数中,然后再将其应用在目标函数上,这实际上是将函数当作参数传入一个函数(高阶函数),而柯里化在其中的作用就是分割,它将装饰函数应用在目标函数然后返回一个装饰过的目标函数,但这个过程不会影响原目标函数,这可能有一些抽象,接下来我们应用实例来说明。
def add(x,y):return x+ydef logger(fn):def wrapper(*args,**kwargs):print("{} function is called. {},{}".format(fn.__name__,args,kwargs))ret = fn(*args,**kwargs)return retreturn wrapperadd = logger(add)我们定义了一个日志修饰函数,这个修饰器的作用就是说明一下目标函数的使用情况,我们使用柯里化将参数分离,这样我们就能不用传入目标函数的参数了,比如说这个add (x,y),如果不使用柯里化,那我们就要传入x,y的值了,但这不是我们注重的部分,我们的目的是将修饰器应用在目标函数上,至于参数是什么,这不是我们考虑的范畴。所以柯里化其实就是把目标函数的参数与目标函数本身分割开,让我们可以更加关注修饰情况。
add = logger(add)我们看到这行代码,其实柯里化的意图已经明显了,我们始终需要的就是这行代码,至于其他参数我们暂时不考虑,而这行代码在python中也作为语法糖(修饰器的语法)变换了存在形式。
在python中,我们用@来表示修饰函数。
装饰器语法
@标识符
标识符指向一个函数,用一个函数来装饰它下面的函数,logger称为装饰器函数,add称为被装饰或被包装函数
本质上来看,无参数装饰器logger实际上等效为一个参数的函数
无参数装饰器 logger
@logger 会把它下面紧挨着的函数的标识符提上来作为它的实参
如此,我们可以写成:
def logger(fn):def wrapper(*args,**kwargs):print("调用前增强功能")print("{} function is called. {},{}".format(fn.__name__,args,kwargs))ret = fn(*args,**kwargs)print("调用后增强功能")return retreturn wrapper@logger
def add(x,y):return x+y
print(add(1,2))以上,就是无参装饰器的基本内容,下一篇我们将讨论有参装饰器的使用。
相关文章:

柯里化与无参装饰器
柯里化 柯里化的概念:柯里化(Currying)在Python中是一种编程技术,它将原本接受多个参数的函数转换为一系列接受单个参数的函数。这种方法以逻辑学家Haskell Curry的名字命名。 简而言之就是将一次函数调用变成先放入一个参数得到…...

Spring事务失效的场景
1. 事务方法执行期间出现了异常,但是并未指定rollbackFor: Spring默认只会在遇到error和RunTimeException时才会回滚。 public boolean rollbackon ( Throwable ex){return (ex instanceof RuntimeException || ex instanceof Error); } 2. 事务方法执行期间出现了…...

Python基础学习之datetime模块
在Python编程中,处理日期和时间是一个常见的需求。Python的datetime模块提供了丰富的类和方法,用于表示和操作日期、时间、时间间隔等。本文将详细介绍Python的datetime模块,并给出一些实用的示例。 1. datetime模块概览 datetime模块是Pyt…...

在AI大模型中全精度和半精度参数是什么意思?
环境: 大模型中 问题描述: 在AI大模型中全精度和半精度参数是什么意思? 解决方案: 在深度学习和高性能计算领域,"全精度"和"半精度"通常指的是模型中使用的数值表示的精度,具体涉…...

刷题记录2
文章目录 刷题记录21047.删除字符串中的所有相邻重复项150.逆波兰表达式求值239.滑动窗口最大值347.前k个高频元素144.二叉树前序遍历(145、94后序、中序)102.二叉树的层序遍历226.翻转二叉树101.对称二叉树104.二叉树的最大深度111.二叉树的最小深度222.完全二叉树的节点个数 …...

【配置】Docker搭建JSON在线解析网站
一个python朋友需要,顺便做一下笔记 正常用菜鸟的就够了,点下面 JSON在线解析 云服务器打开端口8787 连接上docker运行 docker run -id --name jsonhero -p 8787:8787 -e SESSION_SECRETabc123 henryclw/jsonhero-webhttp://ip:8787访问 Github&…...

2024.5.2 —— LeetCode 高频题复盘
目录 151. 反转字符串中的单词129. 求根节点到叶节点数字之和104. 二叉树的最大深度101. 对称二叉树110. 平衡二叉树144. 二叉树的前序遍历543. 二叉树的直径48. 旋转图像98. 验证二叉搜索树39. 组合总和 151. 反转字符串中的单词 题目链接 class Solution:def reverseWords(s…...

ThreeJS:光线投射与3D场景交互
光线投射Raycaster 光线投射详细介绍可参考:https://en.wikipedia.org/wiki/Ray_casting, ThreeJS中,提供了Raycaster类,用于进行鼠标拾取,即:当三维场景中鼠标移动时,利用光线投射,…...
docker挂载数据卷-以nginx为例
目录 一、什么是数据卷 二、数据卷的作用 三、如何挂载数据卷 1、创建nginx容器挂载数据卷 2、查看数据卷 3、查看数据卷详情 4、尝试在宿主机修改数据卷 5、查看容器内对应的数据卷目录 6、 访问nginx查看效果 一、什么是数据卷 挂载数据卷本质上就是实…...

Docker-compose部署Fastapi项目
Docker-compose部署Fastapi、postgres、Redis、Nginx) 之前有写过使用容器部署的方式,这次尝试使用Docker-compose试一次大胆的尝试 使用容器的方式部署只是掌握这项技能的基础,在使用Docker-compose的过程中会有些稍许的不同。毕竟踩过的坑才算是跨过去…...
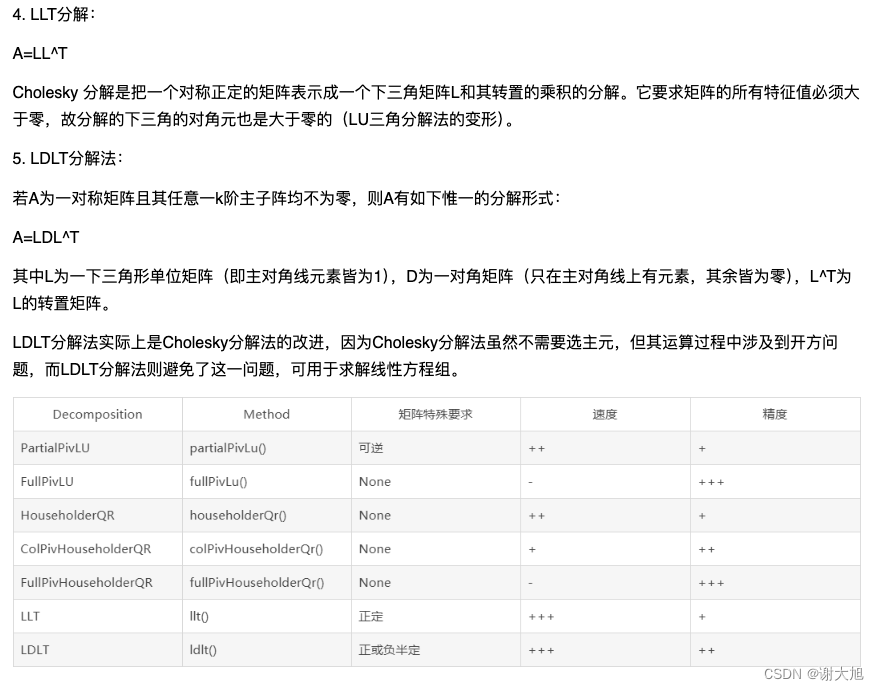
Eigen求解线性方程组
1、线性方程组的应用 线性方程组可以用来解决各种涉及线性关系的问题。以下是一些通常可以用线性方程组来解决的问题: 在实际工程和科学计算中,求解多项式方程的根有着广泛的应用。 在控制系统的设计中,我们经常需要求解特征方程的根来分析…...

7、Java基本数据类型的使用细节探讨(超详细版本)
Java基本数据类型的使用细节探讨 一、整数类型二、浮点数三、字符型四、布尔型 我觉得基本数据类型大家学计算机的应该都懂,但是韩顺平老师讲的基本类型的使用细节我觉得有必要记录一下,重新学的时候才发现有了新的感悟! 一、整数类型 使用细…...
MFC实现点击列表头进行排序
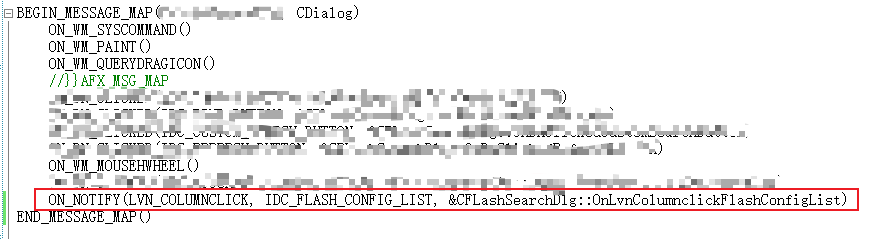
MFC实现点击列表头排序 1、添加消息处理函数 在列表窗口右键,类向导。选择 IDC_LIST1(我的列表控件的ID),消息选择LVN_COLUMNCLICK。 2、消息映射如下 然后会在 cpp 文件中生成以下函数 void CFLashSearchDlg::OnLvnColumnclic…...
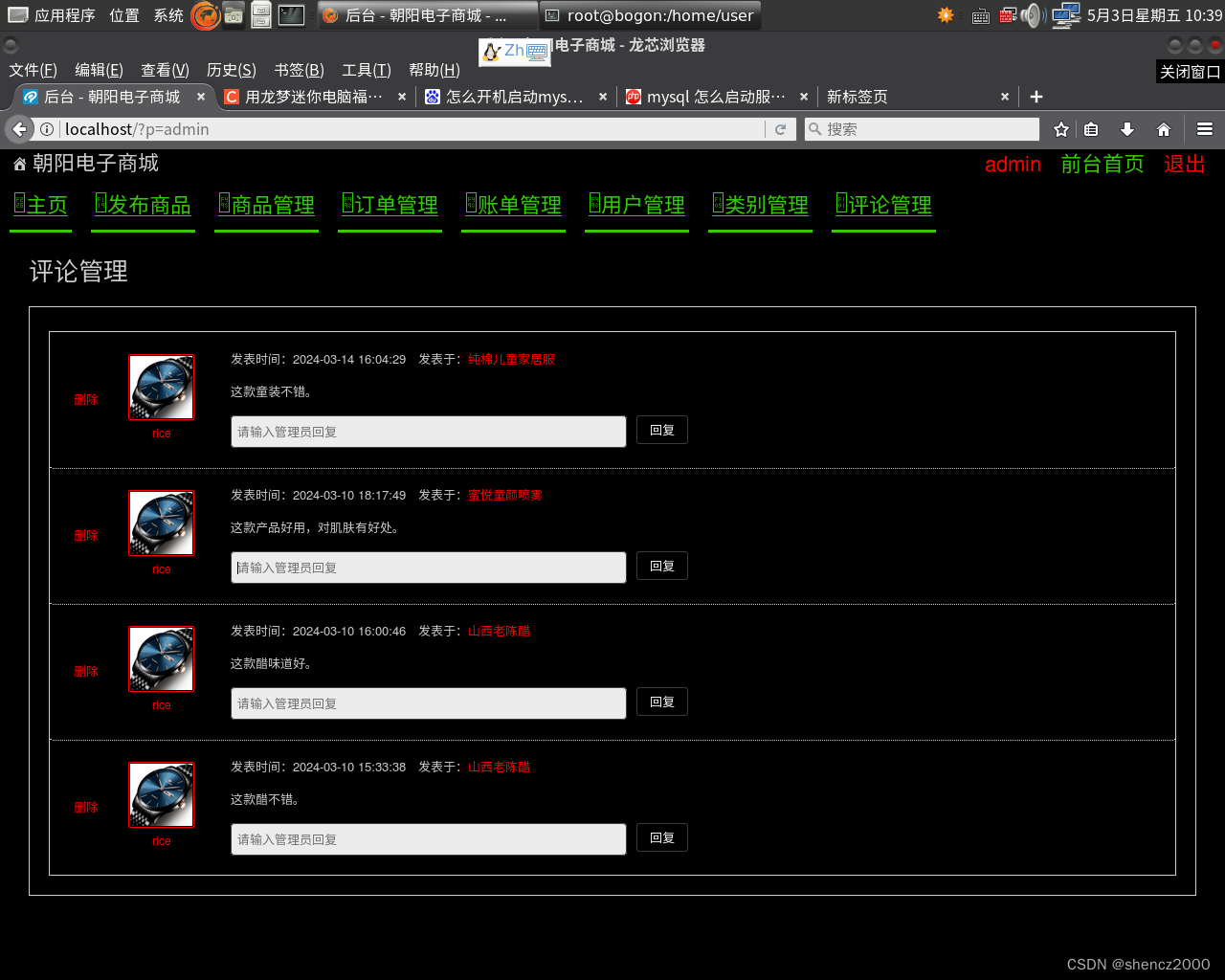
用龙梦迷你电脑福珑2.0做web服务器
用龙梦迷你电脑福珑2.0上做web服务器是可行的。已将一个网站源码放到该电脑,在局域网里可以访问网站网页。另外通过在同一局域网内的一台windows10电脑上安装花生壳软件,也可以在外网访问该内网服务器网站网页。该电脑的操作系统属于LAMP。在该电脑上安装…...

秋招后端开发面试题 - JVM类加载机制
目录 JVM类加载机制前言面试题能说一下类的生命周期吗?类加载的过程知道吗?类加载器有哪些?什么是双亲委派机制?为什么要用双亲委派机制?如何破坏双亲委派机制?如何判断一个类是无用的类? JVM类…...

OceanBase 分布式数据库【信创/国产化】- OceanBase 配置项和系统变量概述
本心、输入输出、结果 文章目录 OceanBase 分布式数据库【信创/国产化】- OceanBase 配置项和系统变量概述前言OceanBase 数据更新架构OceanBase 配置项和系统变量概述配置项配置项分类配置项查询系统变量系统变量分类系统变量查询配置项与系统变量的区分OceanBase 分布式数据库…...

单单单单单の刁队列
在数据结构的学习中,队列是一种常用的线性数据结构,它遵循先进先出(FIFO)的原则。而单调队列是队列的一种变体,它在特定条件下保证了队列中的元素具有某种单调性质,例如单调递增或单调递减。单调队列在处理…...
电脑windows系统压缩解压软件-Bandizip
一、软件功能 Bandizip是一款功能强大的压缩和解压缩软件,具有快速拖放、高速压缩、多核心支持以及广泛的文件格式支持等特点。 Bandizip软件的功能主要包括: 1. 支持多种文件格式 Bandizip可以处理多种压缩文件格式,包括ZIP, 7Z, RAR, A…...
图片公式识别@文档公式识别@表格识别@在线和离线OCR工具
文章目录 abstract普通文字识别本地软件识别公式扩展插件下载小结 在线识别网站/API👺Quicker整合(推荐)可视化编辑和识别公式其他多模态大模型识别图片中的公式排版 开源模型 abstract 本文介绍免费图片文本识别(OCR)工具,包括普通文字识别,公式识别,甚至是手写公…...
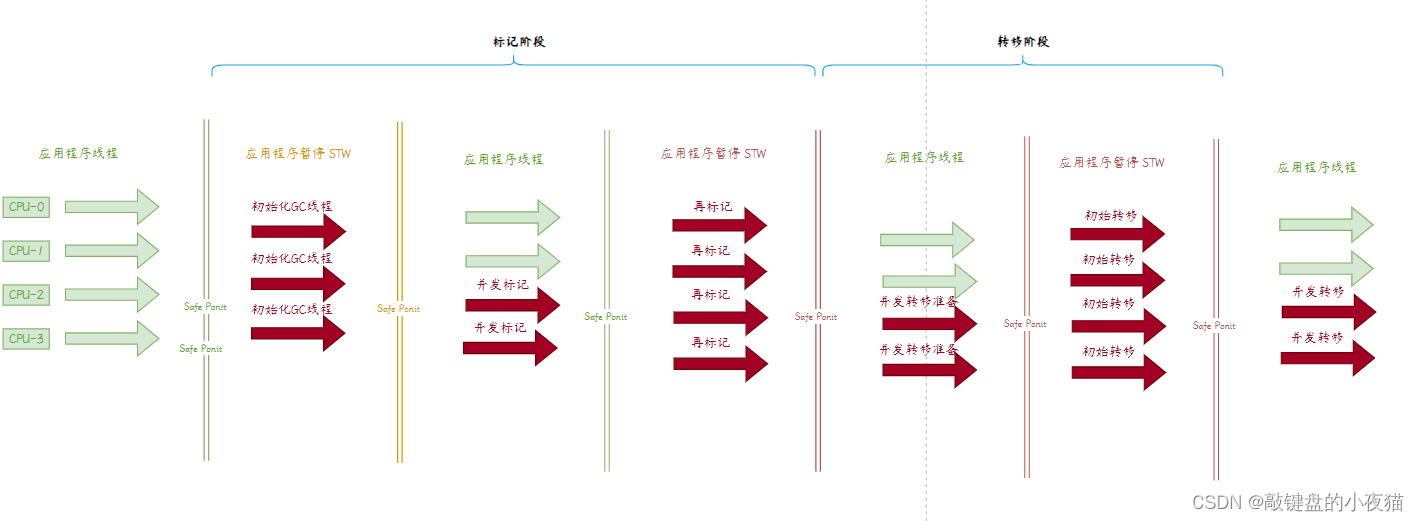
Java高阶私房菜:JVM分代收集算法介绍和各垃圾收集器原理分解
目录 什么是分代收集算法 GC的分类和专业术语 什么是垃圾收集器 垃圾收集器的分类及组合 编辑 应关注的核心指标 Serial和ParNew收集器原理 Serial收集器 ParNew收集器 Parallel和CMS收集器原理 Parallel 收集器 CMS收集器 新一代垃圾收集器G1和ZGC G1垃圾收集器…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...
