代码随想录算法训练营第四十二天| 01背包问题(二维、一维)、416.分割等和子集
系列文章目录
目录
- 系列文章目录
- 动态规划:01背包理论基础
- ①二维数组
- ②一维数组(滚动数组)
- 416. 分割等和子集
- ①回溯法(超时)
- ②动态规划(01背包)
- 未剪枝版
- 剪枝版
动态规划:01背包理论基础
(1)输入读取方法:
-
Scanner sc = new Scanner(System.in);String str = sc.nextLine();int m = Integer.parseInt(str.split(" ")[0]);int n = Integer.parseInt(str.split(" ")[1]);//将String[]数组通过stream流转换成int[]数组int[] weights = Arrays.stream(sc.nextLine().split(" ")).mapToInt(/*s->Integer.parseInt(s)*/Integer::parseInt).toArray();int[] values =Arrays.stream(sc.nextLine().split(" ")).mapToInt(new ToIntFunction<String>() {@Overridepublic int applyAsInt(String value) {return Integer.parseInt(value);}}).toArray(); -
Scanner sc = new Scanner(System.in);// 读取背包容量和物品数量int m = sc.nextInt();int n = sc.nextInt();sc.nextLine(); // 消耗掉输入缓冲区的换行符// 读取物品重量和价值int[] weights = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();int[] values = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray(); -
// 获取输入数据Scanner sc = new Scanner(System.in);int m = sc.nextInt();int n = sc.nextInt();int[] weights = new int[m];for (int i = 0; i < m; i++){weights[i] = sc.nextInt();}int[] values = new int[m];for (int i = 0; i < m; i++){values[i] = sc.nextInt();}
①二维数组
(1)确定dp数组及其含义:
表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
(2)确定递推关系
- 容量不够:一定放不下,直接返回不放
i的最大价值。 - 容量够:根据两种方案的价值做选择,选价值大的。
- 不放
i:相当于在0 ~ (i-1)件物品中选择,容量不变; - 放
i:在确定放i的前提下(腾出空间给i),获取背包能产生的最大价值,再加上i的价值。
- 不放
(3)考虑初始化
初始化第一行:对应物品0,如果背包容量不够,则设置为0,如果够,则设置为values[0];
初始化第一列:对应背包容量0,则无论是什么物品都放不下,不能产生任何价值,直接为默认值0即可。
代码如下:
import java.util.Arrays;
import java.util.Scanner;
import java.util.function.ToIntFunction;public class BagProblem {public static void main(String[] args) {Scanner sc = new Scanner(System.in);String str = sc.nextLine();int m = Integer.parseInt(str.split(" ")[0]);int n = Integer.parseInt(str.split(" ")[1]);//将String[]数组通过stream流转换成int[]数组int[] weights = Arrays.stream(sc.nextLine().split(" ")).mapToInt(/*s->Integer.parseInt(s)*/Integer::parseInt).toArray();int[] values =Arrays.stream(sc.nextLine().split(" ")).mapToInt(new ToIntFunction<String>() {@Overridepublic int applyAsInt(String value) {return Integer.parseInt(value);}}).toArray();//确定dp数组下标及含义:dp[i][j] 表示从下标为0-i的物品里任取,放到容量为j的背包中,价值总和最大为多少int[][] dp = new int[m][n+1];//需要考虑容量和物品数量为0的情况//dp数组初始化for (int i = 0; i < m; i++) {//列初始化dp[i][0] = 0;}for (int j = weights[0]; j <= n; j++) {//行初始化dp[0][j] = values[0];}//确定遍历顺序(先遍历物品再遍历容量或者先遍历容量再遍历背包都行)//①先遍历物品再遍历容量for (int i = 1; i < m; i++) {for (int j = 1; j <= n; j++) {/*** 当前背包的容量都没有当前物品i大的时候,是不放物品i的* 那么前i-1个物品能放下的最大价值就是当前情况的最大价值*/if(j<weights[i]){dp[i][j] = dp[i - 1][j];}else {/*** 当前背包的容量可以放下物品i* 那么此时分两种情况:* 1、不放物品i* 2、放物品i* 比较这两种情况下,哪种背包中物品的最大价值最大*/dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weights[i]] + values[i]);}}}System.out.println(dp[m-1][n]);}
}
②一维数组(滚动数组)
(1)确定dp数组及其含义:
在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。
(2)确定递推关系
- 容量不够:
dp[j],不放物品i。 - 容量够:根据两种方案的价值做选择,选价值大的。
- 不放
i:dp[j],相当于在0 ~ (i-1)件物品中选择,容量不变; - 放
i:dp[j - weight[i]] + value[i],在确定放i的前提下(腾出空间给i),获取背包能产生的最大价值,再加上i的价值。
- 不放
(3)考虑初始化
dp[0]=0,因为背包容量为0所背的物品的最大价值就是0。那么dp数组除了下标0的位置,初始为0,其他下标应该初始化多少呢?看一下递归公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); dp数组在推导的时候一定是取价值最大的数,如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。
import java.util.Arrays;
import java.util.Scanner;
public class BagProblem {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int m = sc.nextInt();int n = sc.nextInt();sc.nextLine();//接收换行符int[] weights = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();int[] values = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();//确定dp数组及含义(背包容量为j的背包所能装的最大价值int[] dp = new int[n + 1];//dp数组初始化dp[0] = 0;//当背包容量为0时,最大价值也为0for (int i = 0; i < m; i++) {//遍历物品for (int j = n; j >= 0; j--) {//遍历容量(倒序遍历)if (j < weights[i]) {dp[j] = dp[j];} else {dp[j] = Math.max(dp[j], dp[j - weights[i]] + values[i]);}}}System.out.println(dp[n]);}
}
416. 分割等和子集
①回溯法(超时)
import java.util.Arrays;public class SplitEqualSumSubsets {public static void main(String[] args) {int[] nums = {3,3,3,4,5};Solution solution = new Solution();boolean answer = solution.canPartition(nums);System.out.println(answer);}
}class Solution {int sum = 0;int tempSum = 0;public boolean canPartition(int[] nums) {for (int i = 0; i < nums.length; i++) {sum += nums[i];}if (sum % 2 != 0) return false;//如果总和为奇数,则无法分割为两个等和子集//对数组从小到大排序Arrays.sort(nums);return backTracking(nums, 0);}public boolean backTracking(int[] nums, int startIndex) {//确定回溯函数的参数及返回值//确定回溯函数终止条件if (tempSum == sum / 2) return true;if (tempSum > sum / 2) {return false;}//确定单层递归逻辑boolean answer1 = false;for (int i = startIndex; i < nums.length; i++) {tempSum += nums[i];answer1 = backTracking(nums, i + 1);if(answer1)return true;// 如果找到一个可行解,立即返回,不再往下遍历tempSum -= nums[i];//回溯}return answer1;}
}
②动态规划(01背包)
未剪枝版
class Solution {public boolean canPartition(int[] nums) {int sum = 0;for (int i = 0; i < nums.length; i++) {sum += nums[i];}//总和为奇数,不能平分if (sum % 2 != 0) return false;//确定dp数组含义(容量为j的背包,放进0~i任意物品后,背的最大重量。int target = sum / 2;int[] dp = new int[target + 1];//dp数组初始化dp[0] = 0;for (int i = 0; i < nums.length; i++) {//先遍历物品for (int j = target; j >= 0; j--) {//倒序遍历背包容量if (j < nums[i]) {dp[j] = dp[j];} else {dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);}//System.out.print(dp[j]);}//System.out.println();}return dp[target] == target;//如果背包装满了,即能找到等和子集}
}
剪枝版
class Solution {public boolean canPartition(int[] nums) {int sum = 0;for (int i = 0; i < nums.length; i++) {sum += nums[i];}//总和为奇数,不能平分if (sum % 2 != 0) return false;//确定dp数组含义(容量为j的背包,放进0~i任意物品后,背的最大重量。int target = sum / 2;int[] dp = new int[target + 1];//dp数组初始化dp[0] = 0;for (int i = 0; i < nums.length; i++) {//先遍历物品for (int j = target; j >= 0; j--) {//倒序遍历背包容量if (j < nums[i]) {dp[j] = dp[j];} else {dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);}//System.out.print(dp[j]);}//System.out.println();//剪枝一下,每一次完成内层的for-loop,立即检查是否dp[target] == target,优化时间复杂度if (dp[target] == target) return true;}return dp[target] == target;//如果背包装满了,即能找到等和子集}
}

相关文章:

代码随想录算法训练营第四十二天| 01背包问题(二维、一维)、416.分割等和子集
系列文章目录 目录 系列文章目录动态规划:01背包理论基础①二维数组②一维数组(滚动数组) 416. 分割等和子集①回溯法(超时)②动态规划(01背包)未剪枝版剪枝版 动态规划:01背包理论基…...

故障——蓝桥杯十三届2022国赛大学B组真题
问题分析 这道题纯数学,考察贝叶斯公式 AC_Code #include <bits/stdc.h> using namespace std; typedef pair<int,double> PI; bool cmp(PI a,PI b){if(a.second!b.second)return a.second>b.second;return a.first<b.first; } int main() {i…...

SSD存储基本知识
存储技术随着时间的推移经历了显著变化,新兴的存储介质正逐步挑战已经成为行业标准的硬盘驱动器(HDD)。在众多竞争者中,固态硬盘(SSD)是最广泛采用且最有潜力占据主导地位的——它们速度快、运行安静&#…...
buuctf-misc题目练习二
ningen 打开题目后是一张图片,放进winhex里面 发现PK,PK是压缩包ZIP 文件的文件头,下一步是想办法进行分离 Foremost可以依据文件内的文件头和文件尾对一个文件进行分离,或者识别当前的文件是什么文件。比如拓展名被删除、被附加…...
Nginx rewrite项目练习
Nginx rewrite练习 1、访问ip/xcz,返回400状态码,要求用rewrite匹配/xcz a、访问/xcz返回400 b、访问/hello时正常访问xcz.html页面server {listen 192.168.99.137:80;server_name 192.168.99.137;charset utf-8;root /var/www/html;location / {root …...

2024,AI手机“元年”? | 最新快讯
文 | 伯虎财经,作者 | 铁观音 2024年,小米、荣耀、vivo、一加、努比亚等品牌的AI手机新品如雨后春笋般涌现。因此,这一年也被业界广泛视为AI手机的“元年” 试想,当你轻触屏幕,你的手机不仅响应你的指令,更…...

5月9(信息差)
🌍 可再生能源发电量首次占全球电力供应的三成 🎄马斯克脑机接口公司 Neuralink 计划将 Link 功能扩展至现实世界,实现控制机械臂、轮椅等 马斯克脑机接口公司 Neuralink 计划将 Link 功能扩展至现实世界,实现控制机械臂、轮椅等…...

leetcode203-Remove Linked List Elements
题目 给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val val 的节点,并返回 新的头节点 。 示例 1: 输入:head [1,2,6,3,4,5,6], val 6 输出:[1,2,3,4,5] 示例 2: 输入&…...

2024付费进群系统,源码及搭建变现视频课程(教程+源码)
自从我做资源站项目盈利稳定后,我越来越对网站类项目感兴趣了,毕竟很多网站类项目还是需要一定技术门槛的,可以过滤掉一些人,很多新人做项目就只盯着短视频,所以网站类项目也就没那么的卷。 这个付费进群系统…...

深入理解Django:中间件与信号处理的艺术
title: 深入理解Django:中间件与信号处理的艺术 date: 2024/5/9 18:41:21 updated: 2024/5/9 18:41:21 categories: 后端开发 tags: Django中间件信号异步性能缓存多语言 引言 在当今的Web开发领域,Django以其强大的功能、简洁的代码结构和高度的可扩…...

rk3588局域网推流
最近无意间看见在网上有使用MediaMtx插件配合ffmpeg在Windows来进行推流,然后在使用其他软件进行拉流显示数据图像的,既然windows都可以使用 ,我想linux应该也可以,正好手上也有一块RK3588的开发板,就测试了一下&#…...

Android虚拟机机制
目录 一、Android 虚拟机 dalvik/art(6版本后)二、Android dex、odex、oat、vdex、art区别 一、Android 虚拟机 dalvik/art(6版本后) 每个应用都在其自己的进程中运行,都有自己的虚拟机实例。ART通过执行DEX文件可在设…...

【触摸案例-手势解锁案例-按钮高亮 Objective-C语言】
一、我们来说这个self.btns,这个问题啊,为什么不用_btns, 1.我们说,在懒加载里边儿,经常是写下划线啊,_btns,为什么不写,首先啊,这个layoutSubviews:我们第一次,肯定会去执行这个layoutSubviews: 然后呢,去懒加载这个数组, 然后呢,接下来啊,走这一句话, 第一次…...
ChatPPT开启高效办公新时代,AI赋能PPT创作
目录 一、前言二、ChatPPT的几种用法1、通过在线生成2、通过插件生成演讲者模式最终成品遇到问题改进建议 三、ChatPPT其他功能 一、前言 想想以前啊,为了做个PPT,我得去网上找各种模板,有时候还得在某宝上花钱买。结果一做PPT,经…...

【C语言项目】贪吃蛇(上)
个人主页 ~ gitee仓库~ 欢迎大家来到C语言系列的最后一个篇章–贪吃蛇游戏的实现,当我们实现了贪吃蛇之后,我们的C语言就算是登堂入室了,基本会使用了,当然,想要更加熟练地使用还需要多多练习 贪吃蛇 一、目标二、需要…...
LeNet-5上手敲代码
LeNet-5 LeNet-5由Yann LeCun在1998年提出,旨在解决手写数字识别问题,被认为是卷积神经网络的开创性工作之一。该网络是第一个被广泛应用于数字图像识别的神经网络之一,也是深度学习领域的里程碑之一。 LeNet-5的整体架构: 总体…...
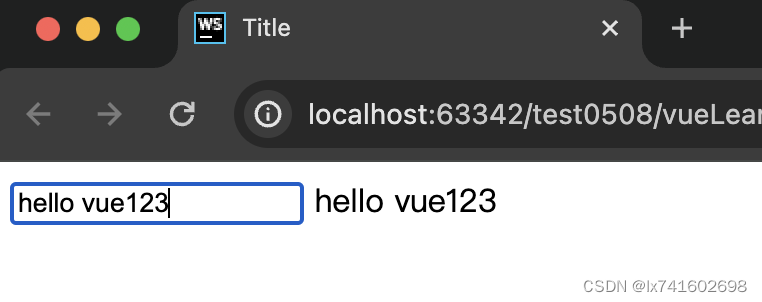
javaWeb入门(自用)
1. vue学习 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>Title</title><script src"https://unpkg.com/vue2"></script> </head> <body><div id"…...

web3风格的网页怎么设计?分享几个,找找感觉。
web3风格的网站是指基于区块链技术和去中心化理念的网站设计风格。这种设计风格强调开放性、透明性和用户自治,体现了Web3的核心价值观。 以下是一些常见的Web3风格网站设计元素: 去中心化标志:在网站的设计中使用去中心化的标志࿰…...

ASP.NET MVC(-)表单的提交、获取表单数据
FromCollection 方式...

[AIGC] 《MyBatis-Plus 结合 Spring Boot 的动态数据源介绍及 Demo 演示》
在现代的 Web 应用开发中,Spring Boot 已经成为了一种流行的框架选择。而 MyBatis-Plus 则为 MyBatis 框架提供了更强大的功能和便利。当它们结合使用时,动态数据源的运用变得更加简单和高效。 动态数据源的概念允许我们在运行时根据不同的条件或需求选…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...
