当前位置： 首页 > news >正文

EtherCAT总线速度轴控制功能块(COSESYS ST源代码)

news 2026/2/11 0:37:45

测试环境为汇川PLC,型号 AM402-CPU1608TP、伺服驱动器为禾川X3E，具体通信配置可以参考下面文章链接：

1、使能和点动控制

汇川AM400PLC通过EtherCAT总线控制禾川X3E伺服使能和点动控制-CSDN博客文章浏览阅读31次。进行通信之前需要安装禾川X3E的XML文件，具体方法如下：1、汇川AM400PLC和X3E通信配置汇川AM400PLC和禾川X3E伺服EtherCAT通信-CSDN博客文章浏览阅读29次。1、汇川H5UPLC和X3E伺服EtherCAT总线控制汇川H5U PLC通过EtherCAT总线控制SV660N和X3E伺服_伺服驱动器 ethercat csdn 汇川-CSDN博客。https://rxxw-control.blog.csdn.net/article/details/1384202752、EtherCAT通信配置

相关文章：

EtherCAT总线速度轴控制功能块(COSESYS ST源代码)

测试环境为汇川PLC,型号 AM402-CPU1608TP、伺服驱动器为禾川X3E，具体通信配置可以参考下面文章链接： 1、使能和点动控制 汇川AM400PLC通过EtherCAT总线控制禾川X3E伺服使能和点动控制-CSDN博客文章浏览阅读31次。进行通信之前需要安装禾川X3E的XML文件，具体方法如下：1、汇…...

编程日记 2024/5/10 3:08:35

【码银送书第十九期】《图算法：行业应用与实践》

作者：嬴图团队 01 前言 在当今工业领域，图思维方式与图数据技术的应用日益广泛，成为图数据探索、挖掘与应用的坚实基础。本文旨在分享嬴图团队在算法实践应用中的宝贵经验与深刻思考，不仅促进业界爱好者之间的交流，…...

编程日记 2024/5/10 3:05:31

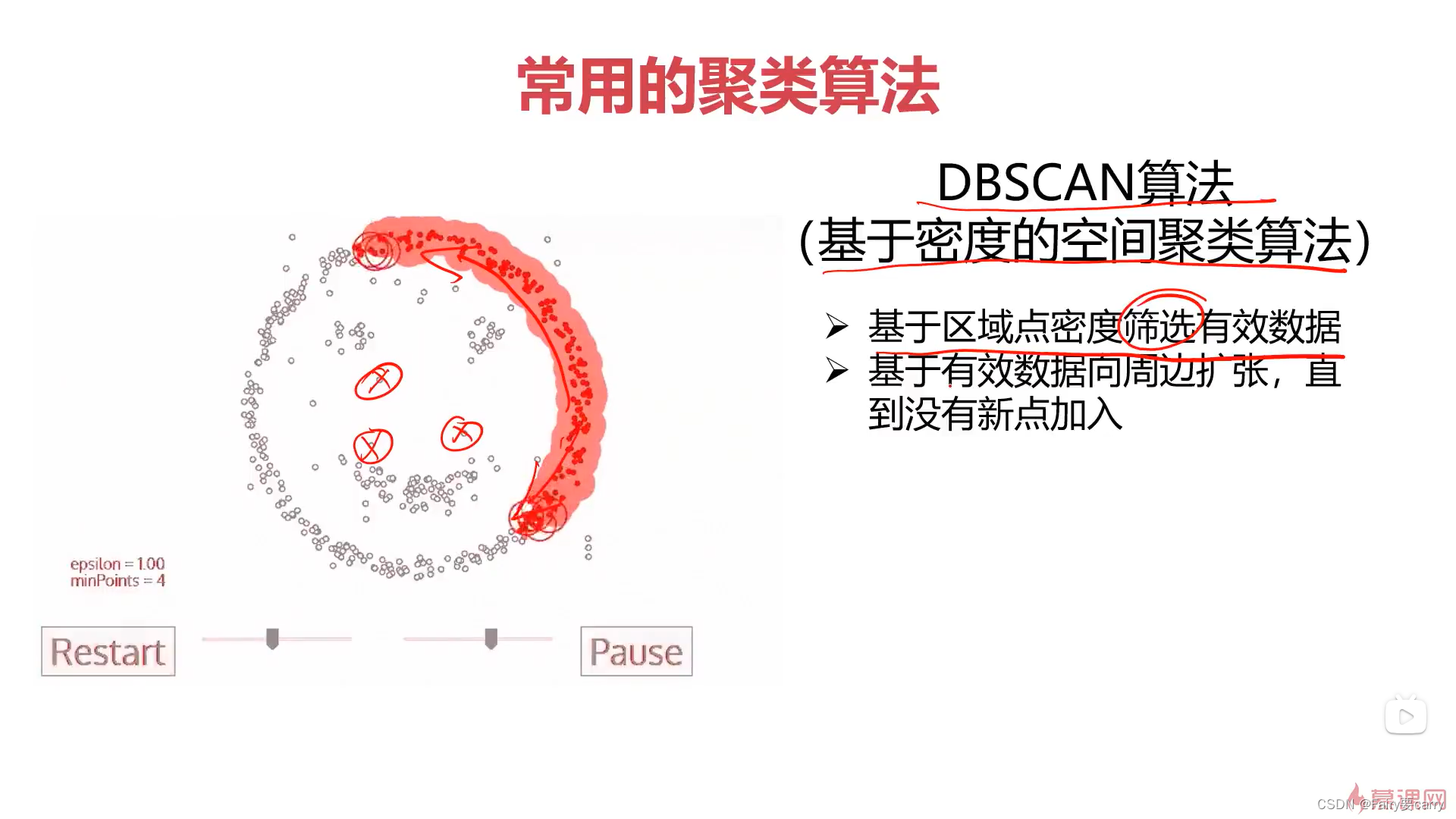
无监督式学习

1.是什么？ 无监督式学习与监督式学习**最大的区别就是：**没有事先给定的训练实例，它是自动对输入的示例进行分类或者分群； 优点：不需要标签数据，极大程度上扩大了我们的数据样本，其次不受监督信…...

编程日记 2024/5/10 3:04:30

docker 安装镜像及使用命令

目录 1. Mysql2. Redis3. Nginx4. Elasticsearch官网指导 docker pull 容器名:版本号 拉取容器, 不指定版本号默认最新的 run 运行 -d 后台运行 -p 3306:3306 -p是port 对外端口:对内端口 –name xyy_mysql 容器名称 -e MYSQL_ROOT_PASSWORD123456 环境变量 -v 系统地址:docker…...

编程日记 2024/5/10 3:03:29

Python运维之多进程！！

本节的快速导航目录如下喔！！！ 一、创建进程的类Process 二、进程并发控制之Semaphore 三、进程同步之Lock 四、进程同步之Event 五、进程优先队列Queue 六、多进程之进程池Pool 七、多进程之数据交换Pipe 一、创建进程的类Process mu…...

编程日记 2024/5/10 3:02:28

Redis（无中心化集群搭建）

文章目录 1.无中心化集群1.基本介绍2.集群说明 2.基本环境搭建1.部署规划（6台服务器）2.首先删除上次的rdb和aof文件（对之前的三台服务器都操作）1.首先分别登录命令行，关闭redis2.清除/root/下的rdb和aof文件3.把上次的…...

编程日记 2024/5/10 3:01:27

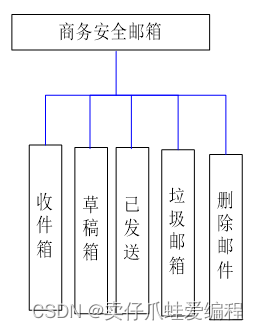
基于springboot+jsp+Mysql的商务安全邮箱邮件收发

开发语言：Java框架：springbootJDK版本：JDK1.8服务器：tomcat7数据库：mysql 5.7（一定要5.7版本）数据库工具：Navicat11开发软件：eclipse/myeclipse/ideaMaven包：…...

编程日记 2024/5/10 3:00:25

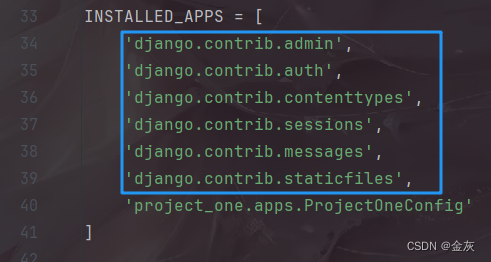
三.Django--ORM(操作数据库)

目录 1 什么是ORM 1.1 ORM优势 1.2ORM 劣势 1.3 ORM与数据库的关系 2 ORM 2.1 作用 2.2 连接数据库 2.3 表操作--设置字段 2.4 数据库的迁移 写路由增删改查操作 项目里的urls.py: app里的views.py: 注意点: 1 什么是ORM ORM中文---对象-关系映射 在MTV,MVC设计…...

编程日记 2024/5/10 2:59:24

【华为】AC直连二层组网隧道转发实验配置

【华为】AC直连二层组网隧道转发实验配置 实验需求拓扑配置AC数据规划表 AC的配置顺序AC1基本配置(二层通信)AP上线VAP组关联--WLAN业务流量 LSW1AR1STA获取AP的业务流量 配置文档 实验需求 AC组网方式：直连二层组网。 业务数据转发方式：隧道转发。 DHC…...

编程日记 2024/5/10 2:58:23

第 129 场 LeetCode 双周赛题解

A 构造相同颜色的正方形 枚举&#xff1a;枚举每个 3 3 3\times 3 33的矩阵&#xff0c;判断是否满足条件 class Solution {public:bool canMakeSquare(vector<vector<char>>& grid) {for (int i 0; i < 2; i)for (int j 0; j < 2; j) {int c1 0, c…...

编程日记 2024/5/10 2:55:20

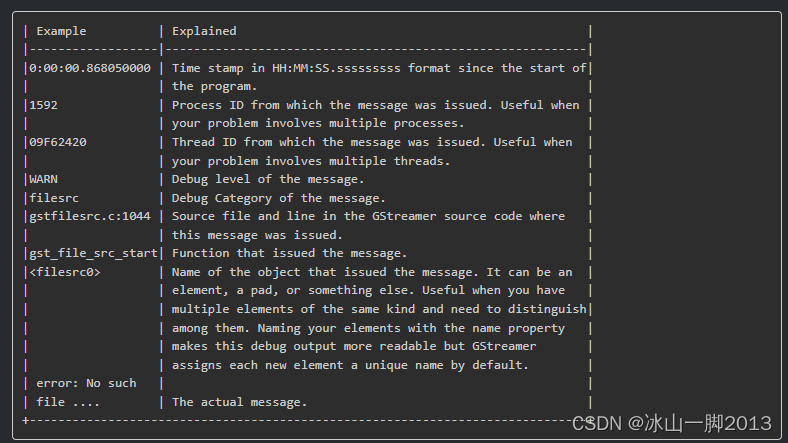
GStreamer日志调试笔记

1、查询所有分类 #gst-launch-1.0 --gst-debug-help 2、查询videotestsrc的日志 #gst-launch-1.0 --gst-debug-help | findstr videotestsrc 结果&#xff1a; 3、使用--gst-debug设置相应日志类型的相应等级&#xff0c;越大显示日志越多&#xff0c;排查内存泄露可以设置为9 …...

编程日记 2024/5/10 2:53:17

【api接口开通教程】YouTube Data API v3申请流程

一、背景调查 1.1 API接口介绍 采集youtube数据&#xff0c;大体分为两种方案&#xff1a;一种是基于爬虫&#xff0c;一种是基于API接口。 说人话就是&#xff1a;爬虫相当于走后门、爬窗户&#xff08;利用技术手段窃取&#xff0c;人家没说给&#xff0c;但我硬拿&#x…...

编程日记 2024/5/10 2:52:15

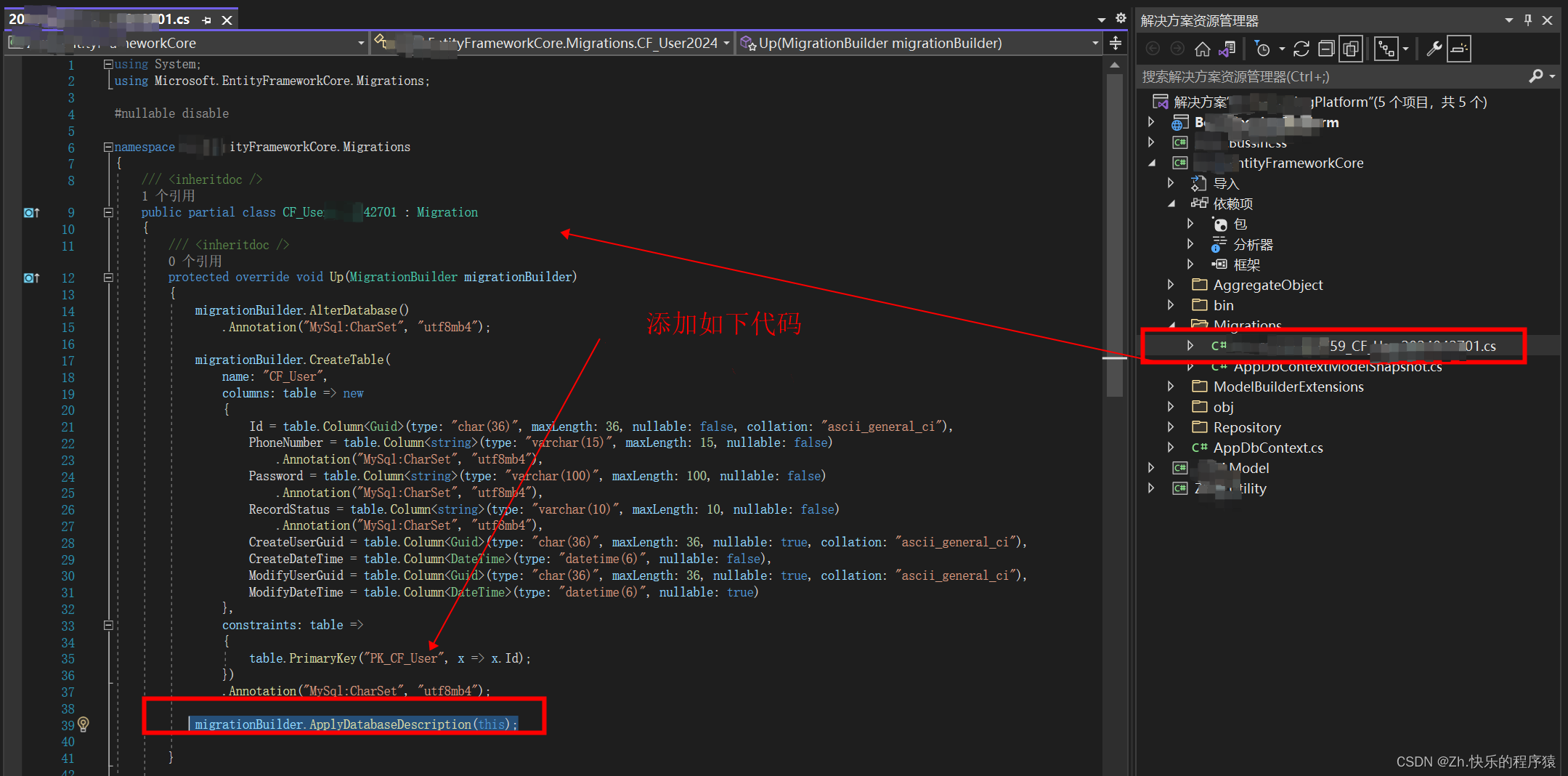
.net 6.0 框架集成ef实战，步骤详解

一、代码框架搭建 搭建如下代码架构&#xff1a; 重点含EntityFrameworkCore工程&#xff0c;该工程中包含AppDbContext.cs和数据表实体AggregateObject 1、AppDbContext 代码案例 //AppDbContext 代码案例using Microsoft.EntityFrameworkCore;namespace EntityFrameworkCo…...

编程日记 2024/5/10 2:50:14

[C/C++] -- 观察者模式

观察者模式是一种行为型设计模式&#xff0c;用于定义对象间的一种一对多的依赖关系&#xff0c;使得当一个对象的状态发生改变时&#xff0c;所有依赖于它的对象都会得到通知并自动更新。 观察者模式涉及以下几个角色&#xff1a; 主题&#xff08;Subject&#xff09;&…...

编程日记 2024/5/10 2:48:12

秋招算法刷题8

20240422 2.两数相加 时间复杂度O&#xff08;max(m,n))&#xff0c;空间复杂度O&#xff08;1&#xff09; public ListNode addTwoNumbers(ListNode l1, ListNode l2) {ListNode headnull,tailnull;int carry0;while(l1!null||l2!null){int n1l1!null?l1.val:0;int n2l2!…...

编程日记 2024/5/10 2:47:10

Docker使用方法

Docker是一种容器化平台&#xff0c;它可以帮助开发人员将应用程序和其依赖项打包成一个独立的、可移植的容器&#xff0c;以便在不同的环境中运行。 以下是使用Docker的基本步骤&#xff1a; 安装Docker&#xff1a;首先&#xff0c;您需要在您的机器上安装Docker。您可以从D…...

编程日记 2024/5/10 2:45:08

HTML学习|网页基本信息、网页基本标签、图像标签、超链接标签、列表标签、表格标签、媒体元素、页面结构分析、iframe内联框架

网页基本信息 DOCTYPE是设置使用什么规范&#xff0c;网页整个信息都在html标签中&#xff0c;head标签里包含字符集设置&#xff0c;网页介绍等信息&#xff0c;title标签是网页的名称&#xff0c;网页的主干都在body标签中 网页基本标签 标题标签 h1~h6都是标题标签&#x…...

编程日记 2024/5/10 2:44:07

001 websocket(评论功能demo)(消息推送)

文章目录 ReviewController.javaWebSocketConfig.javaWebSocketProcess.javaServletInitializer.javaWebsocketApplication.javareadmeindex.htmlapplication.yamlpom.xml ReviewController.java package com.example.controller;import com.example.websocket.WebSocketProces…...

编程日记 2024/5/10 2:41:03

二分查找向下取整导致的死循环69. x 的平方根

二分查找向下取整导致的死循环 考虑伪题目&#xff1a;从数组arr中查找出目标元素target对应的下标&#xff0c;如果数组中不存在目标元素&#xff0c;找 到第一个元素值小于target的元素的下标。 编写二分查找算法如下&#xff1a; Testvoid testBinarySearch(){int[] arr n…...

编程日记 2024/5/10 2:39:00

Kivy 异步任务

如果要进行一些非常耗时的操作(例如&#xff1a;爬虫等)&#xff0c;那么页面就会在这里卡住&#xff0c;而系统就会以为这个软件无响应&#xff0c;并提示关闭&#xff0c;可以说明用户体验极差&#xff0c;因此我们在此处引入异步操作。 在py中引入事件调节器&#xff0c;并在…...

编程日记 2024/5/10 2:35:56

XML Group端口详解

在XML数据映射过程中&#xff0c;经常需要对数据进行分组聚合操作。例如&#xff0c;当处理包含多个物料明细的XML文件时&#xff0c;可能需要将相同物料号的明细归为一组&#xff0c;或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码&#xff0c;增加了开…...

编程新知 2026/2/9 13:51:46

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析

一、变量声明设计&#xff1a;let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性&#xff0c;这种设计体现了语言的核心哲学。以下是深度解析&#xff1a; 1.1 设计理念剖析 安全优先原则&#xff1a;默认不可变强制开发者明确声明意图 let x 5; …...

编程新知 2025/9/28 20:12:12

Linux 文件类型，目录与路径，文件与目录管理

文件类型 后面的字符表示文件类型标志 普通文件&#xff1a;-&#xff08;纯文本文件&#xff0c;二进制文件&#xff0c;数据格式文件&#xff09; 如文本文件、图片、程序文件等。 目录文件&#xff1a;d&#xff08;directory&#xff09; 用来存放其他文件或子目录。 设备…...

编程新知 2026/2/8 20:42:46

Ascend NPU上适配Step-Audio模型

1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统&#xff0c;支持多语言对话&#xff08;如 中文&#xff0c;英文&#xff0c;日语&#xff09;&#xff0c;语音情感&#xff08;如 开心&#xff0c;悲伤&#xff09;&#x…...

编程新知 2026/1/31 4:37:39

CMake 从 GitHub 下载第三方库并使用

有时我们希望直接使用 GitHub 上的开源库，而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例，演示如何： 使用 FetchContent 从 GitH…...

编程新知 2026/2/1 3:19:54

LLMs 系列实操科普（1）

写在前面&#xff1a; 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容&#xff0c;原视频时长 ~130 分钟&#xff0c;以实操演示主流的一些 LLMs 的使用&#xff0c;由于涉及到实操&#xff0c;实际上并不适合以文字整理&#xff0c;但还是决定尽量整理一份笔…...

编程新知 2026/1/31 11:35:24

RSS 2025｜从说明书学习复杂机器人操作任务：NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill

视觉语言模型&#xff08;Vision-Language Models, VLMs&#xff09;&#xff0c;为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展&#xff0c;机器人仍难以胜任复杂的长时程任务&#xff08;如家具装配&#xff09;&#xff0c;主要受限于人…...

编程新知 2026/1/31 5:30:51

怎么让Comfyui导出的图像不包含工作流信息，

为了数据安全&#xff0c;让Comfyui导出的图像不包含工作流信息&#xff0c;导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo&#xff08;推荐&#xff09;​​ 在 save_images 方法中&#xff0c;​​删除或注释掉所有与 metadata …...

编程新知 2025/8/13 15:12:54

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型

在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重&#xff0c;适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解&#xff0c;并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

编程新知 2025/8/8 13:20:37

深入浅出WebGL：在浏览器中解锁3D世界的魔法钥匙

WebGL&#xff1a;在浏览器中解锁3D世界的魔法钥匙 引言&#xff1a;网页的边界正在消失 在数字化浪潮的推动下&#xff0c;网页早已不再是静态信息的展示窗口。如今&#xff0c;我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室&#xff0c;甚至沉浸式的V…...

编程新知 2025/10/31 9:08:31