第 129 场 LeetCode 双周赛题解
A 构造相同颜色的正方形
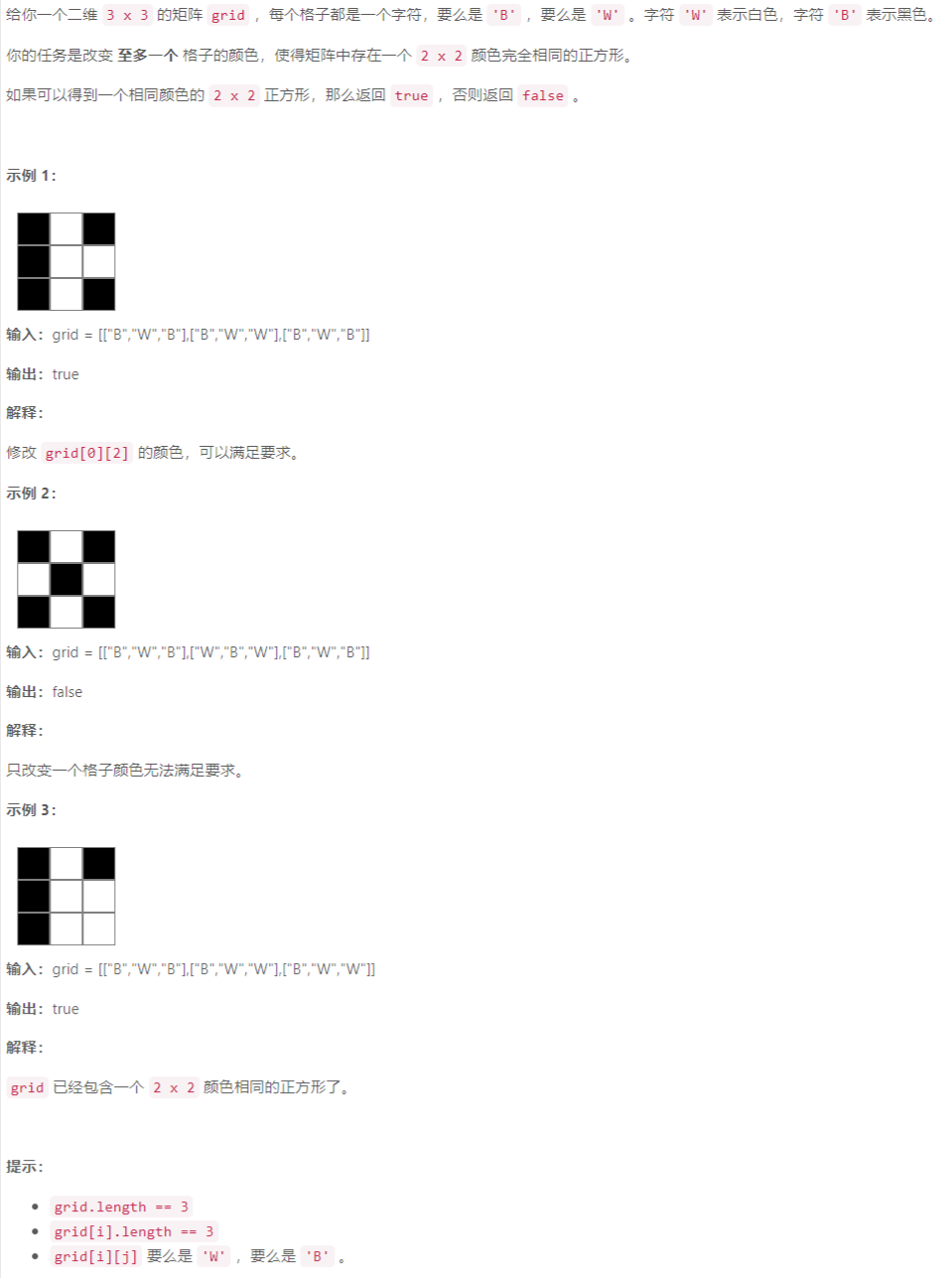
枚举:枚举每个 3 × 3 3\times 3 3×3的矩阵,判断是否满足条件
class Solution {public:bool canMakeSquare(vector<vector<char>>& grid) {for (int i = 0; i < 2; i++)for (int j = 0; j < 2; j++) {int c1 = 0, c2 = 0;for (int r = 0; r < 2; r++)for (int c = 0; c < 2; c++)if (grid[i + r][j + c] == 'B')c1++;elsec2++;if (max(c1, c2) >= 3)return true;}return false;}
};
B 直角三角形
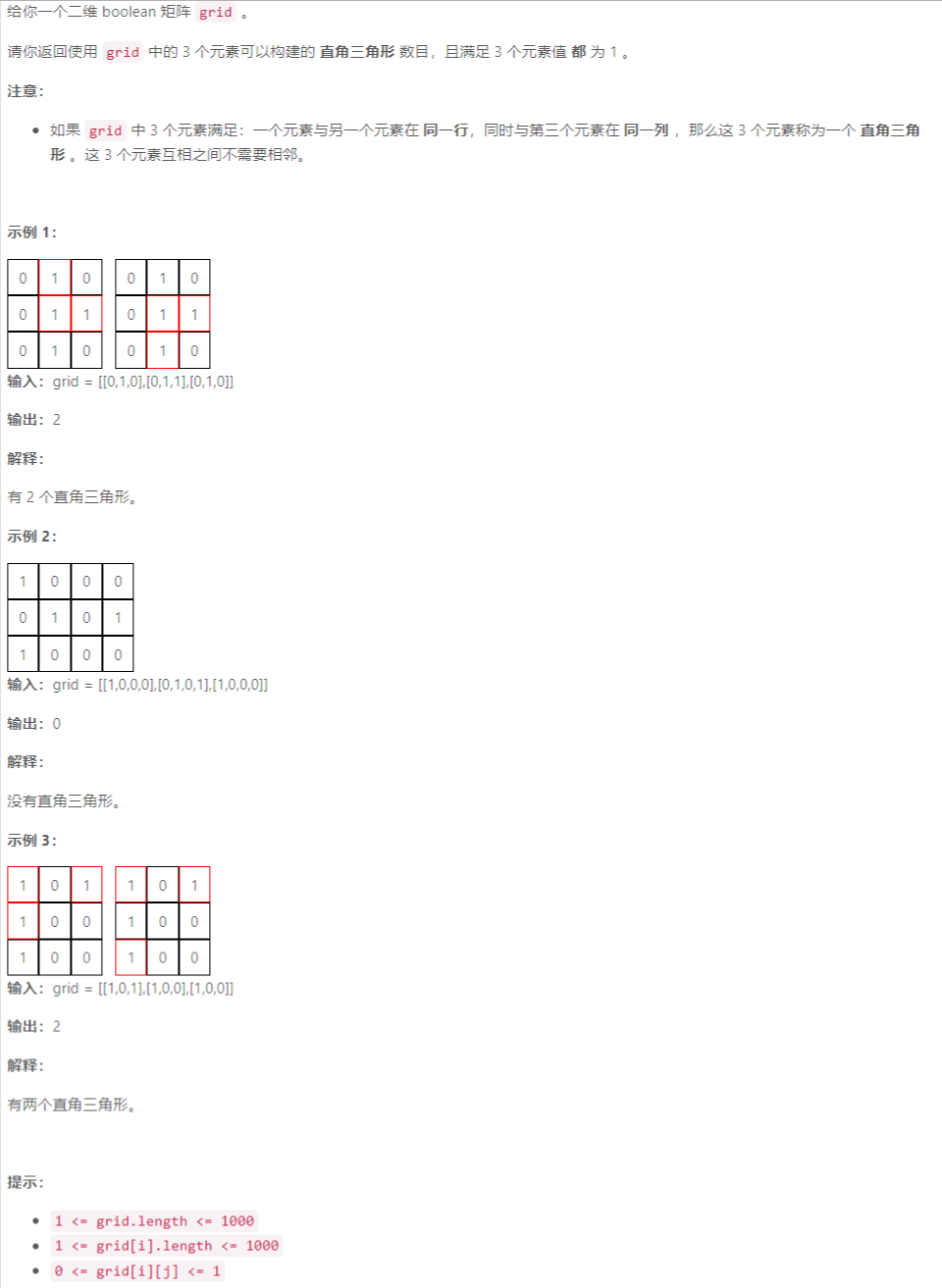
枚举:记录各行各列的 1 1 1 的数目,然后枚举每个直接三角形的直角所在的位置 g r i d [ i ] [ j ] grid[i][j] grid[i][j]
class Solution {public:long long numberOfRightTriangles(vector<vector<int>>& grid) {int m = grid.size(), n = grid[0].size();vector<int> row(m), col(n);for (int i = 0; i < m; i++)for (int j = 0; j < n; j++) {row[i] += grid[i][j];col[j] += grid[i][j];}long long res = 0;for (int i = 0; i < m; i++)for (int j = 0; j < n; j++)if (grid[i][j])res += 1LL * (row[i] - 1) * (col[j] - 1);return res;}
};
C 找出所有稳定的二进制数组 I

动态规划:设 p [ i ] [ j ] [ t a i l ] p[i][j][tail] p[i][j][tail] 为含有 i i i 个 0 0 0 和 j j j 个 1 1 1 且以 t a i l tail tail 为结尾的稳定二进制数组的个数,可以枚举其全为 t a i l tail tail 的后缀数组的可能长度来进行状态转移
class Solution {public:using ll = long long;ll mod = 1e9 + 7;int numberOfStableArrays(int zero, int one, int limit) {ll p[zero + 1][one + 1][2]; memset(p, 0, sizeof(p));for (int cz = 1; cz <= zero && cz <= limit; ++cz)p[cz][0][0] = 1;for (int co = 1; co <= one && co <= limit; ++co)p[0][co][1] = 1;for (int i = 0; i <= zero; i++) {for (int j = 0; j <= one; j++) {for (int last = 1; last <= limit; last++) {//全为tail的后缀数组的长度为lastif (i - last >= 0)p[i][j][0] = (p[i][j][0] + p[i - last][j][1]) % mod;if (j - last >= 0)p[i][j][1] = (p[i][j][1] + p[i][j - last][0]) % mod;}}}return ((p[zero][one][0] + p[zero][one][1]) % mod + mod) % mod;}
};
D 找出所有稳定的二进制数组 II

动态规划:设 p [ i ] [ j ] [ t a i l ] p[i][j][tail] p[i][j][tail] 为含有 i i i 个 0 0 0 和 j j j 个 1 1 1 且以 t a i l tail tail 为结尾的稳定二进制数组的个数,枚举其全为 t a i l tail tail 的后缀数组的可能长度来进行状态转移,可以通过维护两个前缀和来优化状态转移的时间复杂度
class Solution {public:using ll = long long;ll mod = 1e9 + 7;int numberOfStableArrays(int zero, int one, int limit) {ll p[zero + 1][one + 1][2]; ll ps0[zero + 1][one + 1];ll ps1[zero + 1][one + 1];memset(p, 0, sizeof(p));memset(ps0, 0, sizeof(ps0));memset(ps1, 0, sizeof(ps1));for (int i = 1; i <= zero && i <= limit; ++i) {p[i][0][0] = 1;ps0[i][0] = 1;}for (int j = 1; j <= one && j <= limit; ++j) {p[0][j][1] = 1;ps1[0][j] = 1;}for (int i = 0; i <= zero; i++) {for (int j = 0; j <= one; j++) {// [max(0,i-limit),i-1]if (int l = max(0, i - limit), r = i - 1; l <= r)p[i][j][0] += l != 0 ? (ps1[r][j] - ps1[l - 1][j]) % mod : ps1[r][j];if (int l = max(0, j - limit), r = j - 1; l <= r)p[i][j][1] += l != 0 ? (ps0[i][r] - ps0[i][l - 1]) % mod : ps0[i][r];if (j)ps0[i][j] = (ps0[i][j - 1] + p[i][j][0]) % mod;if (i)ps1[i][j] = (ps1[i - 1][j] + p[i][j][1]) % mod;}}return ((p[zero][one][0] + p[zero][one][1]) % mod + mod) % mod;}
};
相关文章:

第 129 场 LeetCode 双周赛题解
A 构造相同颜色的正方形 枚举:枚举每个 3 3 3\times 3 33的矩阵,判断是否满足条件 class Solution {public:bool canMakeSquare(vector<vector<char>>& grid) {for (int i 0; i < 2; i)for (int j 0; j < 2; j) {int c1 0, c…...
GStreamer日志调试笔记
1、查询所有分类 #gst-launch-1.0 --gst-debug-help 2、查询videotestsrc的日志 #gst-launch-1.0 --gst-debug-help | findstr videotestsrc 结果: 3、使用--gst-debug设置相应日志类型的相应等级,越大显示日志越多,排查内存泄露可以设置为9 …...

【api接口开通教程】YouTube Data API v3申请流程
一、背景调查 1.1 API接口介绍 采集youtube数据,大体分为两种方案:一种是基于爬虫,一种是基于API接口。 说人话就是:爬虫相当于走后门、爬窗户(利用技术手段窃取,人家没说给,但我硬拿&#x…...
.net 6.0 框架集成ef实战,步骤详解
一、代码框架搭建 搭建如下代码架构: 重点含EntityFrameworkCore工程,该工程中包含AppDbContext.cs和数据表实体AggregateObject 1、AppDbContext 代码案例 //AppDbContext 代码案例using Microsoft.EntityFrameworkCore;namespace EntityFrameworkCo…...

[C/C++] -- 观察者模式
观察者模式是一种行为型设计模式,用于定义对象间的一种一对多的依赖关系,使得当一个对象的状态发生改变时,所有依赖于它的对象都会得到通知并自动更新。 观察者模式涉及以下几个角色: 主题(Subject)&…...

秋招算法刷题8
20240422 2.两数相加 时间复杂度O(max(m,n)),空间复杂度O(1) public ListNode addTwoNumbers(ListNode l1, ListNode l2) {ListNode headnull,tailnull;int carry0;while(l1!null||l2!null){int n1l1!null?l1.val:0;int n2l2!…...

Docker使用方法
Docker是一种容器化平台,它可以帮助开发人员将应用程序和其依赖项打包成一个独立的、可移植的容器,以便在不同的环境中运行。 以下是使用Docker的基本步骤: 安装Docker:首先,您需要在您的机器上安装Docker。您可以从D…...

HTML学习|网页基本信息、网页基本标签、图像标签、超链接标签、列表标签、表格标签、媒体元素、页面结构分析、iframe内联框架
网页基本信息 DOCTYPE是设置使用什么规范,网页整个信息都在html标签中,head标签里包含字符集设置,网页介绍等信息,title标签是网页的名称,网页的主干都在body标签中 网页基本标签 标题标签 h1~h6都是标题标签&#x…...
(消息推送))
001 websocket(评论功能demo)(消息推送)
文章目录 ReviewController.javaWebSocketConfig.javaWebSocketProcess.javaServletInitializer.javaWebsocketApplication.javareadmeindex.htmlapplication.yamlpom.xml ReviewController.java package com.example.controller;import com.example.websocket.WebSocketProces…...
二分查找向下取整导致的死循环69. x 的平方根
二分查找向下取整导致的死循环 考虑伪题目:从数组arr中查找出目标元素target对应的下标,如果数组中不存在目标元素,找 到第一个元素值小于target的元素的下标。 编写二分查找算法如下: Testvoid testBinarySearch(){int[] arr n…...

Kivy 异步任务
如果要进行一些非常耗时的操作(例如:爬虫等),那么页面就会在这里卡住,而系统就会以为这个软件无响应,并提示关闭,可以说明用户体验极差,因此我们在此处引入异步操作。 在py中引入事件调节器,并在…...
))
DEV--C++小游戏(吃星星(0.1))
目录 吃星星(0.1) 简介 头文件 命名空间变量 副函数 清屏函数 打印地图函数 移动函数 主函数 0.1版完整代码 吃星星(0.1) 注:版本<1为未实现或只实现部分 简介 用wasd去吃‘*’ 头文件 #include<bi…...

LINUX 入门 4
LINUX 入门 4 day6 7 20240429 20240504 耗时:240min 课程链接地址 第4章 LINUX环境编程——实现线程池 C基础 第3节 #define里面的行不能乱空行,要换行就打\ typedef 是 C 和 C 中的一个关键字,用于为已有的数据类型定义一个新的名字。…...
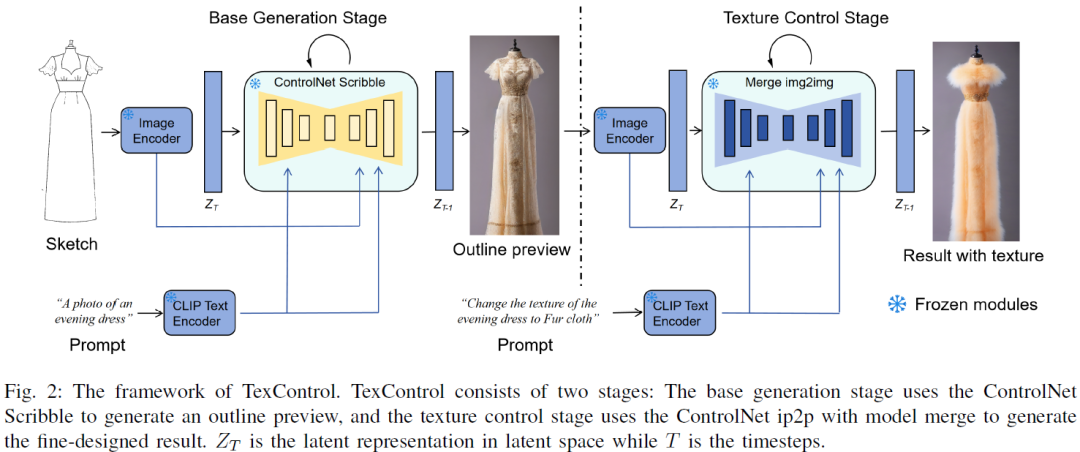
Imagine Flash、StyleMamba 、FlexControl、Multi-Scene T2V、TexControl
本文首发于公众号:机器感知 Imagine Flash、StyleMamba 、FlexControl、Multi-Scene T2V、TexControl You Only Cache Once: Decoder-Decoder Architectures for Language Models We introduce a decoder-decoder architecture, YOCO, for large language models, …...
 方法详解)
Java Collections.emptyList() 方法详解
前言 在Java开发的日常中,我们常常需要处理集合数据结构,而这其中就免不了要面对“空集合”的场景。传统的做法可能是直接返回 null,但这往往会引入空指针异常的风险,降低了代码的健壮性。幸运的是,Java为我们提供了一…...
Vue前端环境准备
vue-cli Vue-cli是Vue官方提供的脚手架,用于快速生成一个Vue项目模板 提供功能: 统一的目录结构 本地调试 热部署 单元测试 集成打包上线 依赖环境:NodeJs 安装NodeJs与Vue-Cli 1、安装nodejs(已经安装就不用了) node-…...

代码随想录算法训练营第四十二天| 01背包问题(二维、一维)、416.分割等和子集
系列文章目录 目录 系列文章目录动态规划:01背包理论基础①二维数组②一维数组(滚动数组) 416. 分割等和子集①回溯法(超时)②动态规划(01背包)未剪枝版剪枝版 动态规划:01背包理论基…...

故障——蓝桥杯十三届2022国赛大学B组真题
问题分析 这道题纯数学,考察贝叶斯公式 AC_Code #include <bits/stdc.h> using namespace std; typedef pair<int,double> PI; bool cmp(PI a,PI b){if(a.second!b.second)return a.second>b.second;return a.first<b.first; } int main() {i…...

SSD存储基本知识
存储技术随着时间的推移经历了显著变化,新兴的存储介质正逐步挑战已经成为行业标准的硬盘驱动器(HDD)。在众多竞争者中,固态硬盘(SSD)是最广泛采用且最有潜力占据主导地位的——它们速度快、运行安静&#…...
buuctf-misc题目练习二
ningen 打开题目后是一张图片,放进winhex里面 发现PK,PK是压缩包ZIP 文件的文件头,下一步是想办法进行分离 Foremost可以依据文件内的文件头和文件尾对一个文件进行分离,或者识别当前的文件是什么文件。比如拓展名被删除、被附加…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...
