代码随想录算法训练营DAY45|C++动态规划Part7|70.爬楼梯(进阶版)、322. 零钱兑换、279.完全平方数
文章目录
- 70.爬楼梯(进阶版)
- ⭐️322. 零钱兑换
- 思路
- CPP代码
- 总结
- 279.完全平方数
- 思路
- CPP代码
70.爬楼梯(进阶版)
卡码网:57. 爬楼梯
文章讲解:70.爬楼梯(进阶版)
本题就是典型了完全背包排列问题,也没有什么绕弯,比较简单
#include <bits/stdc++.h>
using namespace std;int main () {int m, n;cin >> n >> m;std::vector<int> dp(n + 1, 0);dp[0] = 1;for (int j = 1; j <= n; j++) {for (int i = 0; i <= m; i++) {if (j >= i)dp[j] += dp[j - i]; }}cout << dp[n] << endl;return 0;
}
⭐️322. 零钱兑换
力扣题目链接
文章讲解:322. 零钱兑换
视频讲解:装满背包最少的物品件数是多少?| LeetCode:322.零钱兑换
在这里,我先总结一下之前写过的题目
在518.零钱兑换II中,我们求的是装满这个背包有多少种办法,求的是不强调元素顺序的组合数,递推公式是dp[j]+=dp[j-coins[i]]
在377. 组合总和 Ⅳ中,我们也求的是装满这个背包有多少种方法,但是求的是强调元素顺序的排列数,递推公式也是dp[j]+=dp[j-coins[i]],但是我们的遍历顺序是外层for遍历背包,内层for循环遍历物品
本题中,我们求的是装满这个背包最少用多少件物品
思路
- 确定dp数组的含义
本题中要装满容量为account的背包,最少的物品。那么很直观我们的dp数组的含义就是装满容量为j的背包,所需要的最少物品数量为dp[j]
- 递推公式
首先我们放物品应该如何表达?
如果我们要装满一个j-coins(i)容量大背包,所需要的最少物品为dp[j-coins(i)],那我现在要装一个j容量的背包,dp[j]可以有一种取值是dp[j] = dp[j-coins(i)]+1(因为我们在遍历coins[i]),那现在我要求一个装满j容量的最小值,那肯定就是
d p [ j ] = m i n ( d p [ j − c o i n s ( i ) ] + 1 , d p [ j ] ) dp[j] = min(dp[j-coins(i)]+1, dp[j]) dp[j]=min(dp[j−coins(i)]+1,dp[j])
- 初始化
聊到初始化,我们首先就要像dp[0]等于多少,很明显,根据题目含义,account=0的话,我们什么都不放就可以凑成这个account了。
之前我们把非0下标的值初始成0是为了防止我们在递推公式求的值被初始值覆盖,因为我们之前都是dp=max(...),但是在本题中,我们的递推公式出现的是dp[j]=min(...),所以我们应该把非零下标初始成INT_MAX。这样我们在推导赋值的时候才不会被初始值给覆盖掉
- 遍历顺序
还记得377. 组合总和 Ⅳ这篇文章遍历顺序部分,我们做了一个小总结,先遍历物品在遍历背包求的是组合数;先遍历背包再遍历物品求的就是排列数。
在本题中,我们求的是最少物品是多少,所以本题和组合排列没什么关系,不影响我们最终要求的最少的元素数量,故本题什么样的遍历顺序都可以。
- 打印
以输入:coins = [1, 2, 5], amount = 5为例 dp[amount]为最终结果。

CPP代码
// 版本一 先物品,再背包
class Solution {
public:int coinChange(vector<int>& coins, int amount) {vector<int> dp(amount + 1, INT_MAX);dp[0] = 0;for (int i = 0; i < coins.size(); i++) { // 遍历物品for (int j = coins[i]; j <= amount; j++) { // 遍历背包if (dp[j - coins[i]] != INT_MAX) { // 如果dp[j - coins[i]]是初始值则跳过dp[j] = min(dp[j - coins[i]] + 1, dp[j]);}}}if (dp[amount] == INT_MAX) return -1;return dp[amount];}
};// 版本二 先背包,再物品
class Solution {
public:int coinChange(vector<int>& coins, int amount) {vector<int> dp(amount + 1, INT_MAX);dp[0] = 0;for (int i = 1; i <= amount; i++) { // 遍历背包for (int j = 0; j < coins.size(); j++) { // 遍历物品if (i - coins[j] >= 0 && dp[i - coins[j]] != INT_MAX ) {dp[i] = min(dp[i - coins[j]] + 1, dp[i]);}}}if (dp[amount] == INT_MAX) return -1;return dp[amount];}
};
- 时间复杂度: O(n * amount),其中 n 为 coins 的长度
- 空间复杂度: O(amount)
总结
装满背包最少要多少物品 的递推公式要重点关注,再一个就是关于初始值的设定也很有讲究。
279.完全平方数
力扣题目链接
视频讲解:换汤不换药!| LeetCode:279.完全平方数
文章讲解:279.完全平方数
状态:典型的背包问题!真的就是换汤不换药
很明显,我们这里的n就是我们的背包容量,然后物品的重量和价值就是各个完全平方数,题目中要求的是用完全平方数拼凑出n的最小个数,这不就是妥妥的上一题
322.零钱兑换的思路?也就是说求的是装满这个背包所需要的最少物品的数量
思路
- dp数组的含义
看完上面对题目的论述,本题直接j表示背包容量,dp[j]表示能装满背包所需要的最少物品。
- 递归函数
跟上一题一样,直接是dp[j] = min(dp[j - i * i] + 1, dp[j])
- 初始化
dp[0]表示 和为0的完全平方数的最小数量,那么dp[0]一定是0。
同理,从递归公式dp[j] = min(dp[j - i * i] + 1, dp[j])中可以看出每次dp[j]都要选最小的,所以非0下标的dp[j]一定要初始为最大值INT_MAX,这样dp[j]在递推的时候才不会被初始值覆盖。
- 遍历顺序
与上一题一样,本题外层for遍历背包,内层for遍历物品,还是外层for遍历物品,内层for遍历背包,都是可以的!
- 打印
略
CPP代码
// 版本一
class Solution {
public:int numSquares(int n) {vector<int> dp(n + 1, INT_MAX);dp[0] = 0;for (int i = 0; i <= n; i++) { // 遍历背包for (int j = 1; j * j <= i; j++) { // 遍历物品dp[i] = min(dp[i - j * j] + 1, dp[i]);}}return dp[n];}
};// 版本二
class Solution {
public:int numSquares(int n) {vector<int> dp(n + 1, INT_MAX);dp[0] = 0;for (int i = 1; i * i <= n; i++) { // 遍历物品for (int j = i * i; j <= n; j++) { // 遍历背包dp[j] = min(dp[j - i * i] + 1, dp[j]);}}return dp[n];}
};
- 时间复杂度: O(n * √n)
- 空间复杂度: O(n)
相关文章:

代码随想录算法训练营DAY45|C++动态规划Part7|70.爬楼梯(进阶版)、322. 零钱兑换、279.完全平方数
文章目录 70.爬楼梯(进阶版)⭐️322. 零钱兑换思路CPP代码总结 279.完全平方数思路CPP代码 70.爬楼梯(进阶版) 卡码网:57. 爬楼梯 文章讲解:70.爬楼梯(进阶版) 本题就是典型了完全背包排列问题,…...

Linux(openEuler、CentOS8)企业内网DHCP服务器搭建(固定Mac获取指定IP)
----本实验环境为openEuler系统<以server方式安装>(CentOS8基本一致,可参考本文)---- 目录 一、知识点二、实验(一)为服务器配置网卡和IP(二)为服务器安装DHCP服务软件(三&a…...

c#读取hex文件方法,相对来说比较清楚
Hex文件解读_c#读取hex文件-CSDN博客 https://wenku.csdn.net/answer/d67f30cf834c435ca37c3d1ef5e78a62?ops_request_misc%257B%2522request%255Fid%2522%253A%2522171498156816800227423661%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&…...
【ytb数据采集器】按关键词批量爬取视频数据,界面软件更适合文科生!
一、背景介绍 1.1 爬取目标 用Python独立开发的爬虫工具,作用是:通过搜索关键词采集油管的搜索结果,包含14个关键字段:关键词,页码,视频标题,视频id,视频链接,发布时间,视频时长,频道名称,频道id,频道链接,播放数,点赞数,评论数…...

三条命令快速配置Hugging Face
大家好啊,我是董董灿。 本文给出一个配置Hugging Face的方法,让你在国内可快速从Hugging Face上下在模型和各种文件。 1. 什么是 Hugging Face Hugging Face 本身是一家科技公司,专注于自然语言处理(NLP)和机器学习…...

Python网络编程 03 实验:FTP详解
文章目录 一、小实验FTP程序需求二、项目文件架构三、服务端1、conf/settings.py2、conf/accounts.cgf3、conf/STATUS_CODE.py4、启动文件 bin/ftp_server.py5、core/main.py6、core/server.py 四、客户端1、conf/STATUS_CODE.py2、bin/ftp_client.py 五、在终端操作示例 一、小…...
)
个人银行账户管理程序(2)
在(1)的基础上进行改进 1:增加一个静态成员函数total,记录账户总金额和静态成员函数getTotal 2对不需要改变的对象进行const修饰 3多文件实现 account。h文件 #ifndef _ACCOUNT_ #define _ACCOUNT_ class SavingAccount {pri…...

2024.04.19校招 实习 内推 面经
绿*泡*泡VX: neituijunsir 交流*裙 ,内推/实习/校招汇总表格 1、校招&转正实习 | 美团无人机业务部招聘(内推) 校招&转正实习 | 美团无人机业务部招聘(内推) 2、校招&实习 | 快手 这些岗位…...

Python并发编程 04 进程与线程基础
文章目录 一、操作系统简介二、进程三、线程四、线程的调用1、示例2、join方法3、setDaemon方法4、继承式调用(不推荐)5、其他方法 一、操作系统简介 ①操作系统是一个用来协调、管理和控制计算机硬件和软件资源的系统程序,它位于硬件和应用…...
模板引擎Freemarker
什么是模板引擎 根据前边的数据模型分析,课程预览就是把课程的相关信息进行整合,在课程预览界面进行展示,课程预览界面与课程发布的课程详情界面一致。 项目采用模板引擎技术实现课程预览界面。什么是模板引擎? 早期我们采用的…...

刷题训练之模拟
> 作者:დ旧言~ > 座右铭:松树千年终是朽,槿花一日自为荣。 > 目标:熟练掌握模拟算法。 > 毒鸡汤:学习,学习,再学习 ! 学,然后知不足。 > 专栏选自:刷题训…...

视频监控平台:交通运输标准JTT808设备SDK接入源代码函数分享
目录 一、JT/T 808标准简介 (一)概述 (二)协议特点 1、通信方式 2、鉴权机制 3、消息分类 (三)协议主要内容 1、位置信息 2、报警信息 3、车辆控制 4、数据转发 二、代码和解释 (一…...
)
【C++】多态 — 多态的细节补充(下篇)
前言: 我们学习了多态的形式和如何使用多态,这一章我们将来讲一讲多态的原理… 目录 动态绑定与静态绑定: 动态绑定与静态绑定: 静态绑定又称为前期绑定(早绑定),在程序编译期间确定了程序的行为,也称为静态多态,比如…...
系统安全与应用【2】
1.开关机安全控制 1.1 GRUB限制 限制更改GRUB引导参数 通常情况下在系统开机进入GRUB菜单时,按e键可以查看并修改GRUB引导参数,这对服务器是一个极大的威胁。可以为GRUB 菜单设置一个密码,只有提供正确的密码才被允许修改引导参数。 实例&…...
EtherCAT总线速度轴控制功能块(COSESYS ST源代码)
测试环境为汇川PLC,型号 AM402-CPU1608TP、伺服驱动器为禾川X3E,具体通信配置可以参考下面文章链接: 1、使能和点动控制 汇川AM400PLC通过EtherCAT总线控制禾川X3E伺服使能和点动控制-CSDN博客文章浏览阅读31次。进行通信之前需要安装禾川X3E的XML文件,具体方法如下:1、汇…...

【码银送书第十九期】《图算法:行业应用与实践》
作者:嬴图团队 01 前言 在当今工业领域,图思维方式与图数据技术的应用日益广泛,成为图数据探索、挖掘与应用的坚实基础。本文旨在分享嬴图团队在算法实践应用中的宝贵经验与深刻思考,不仅促进业界爱好者之间的交流,…...
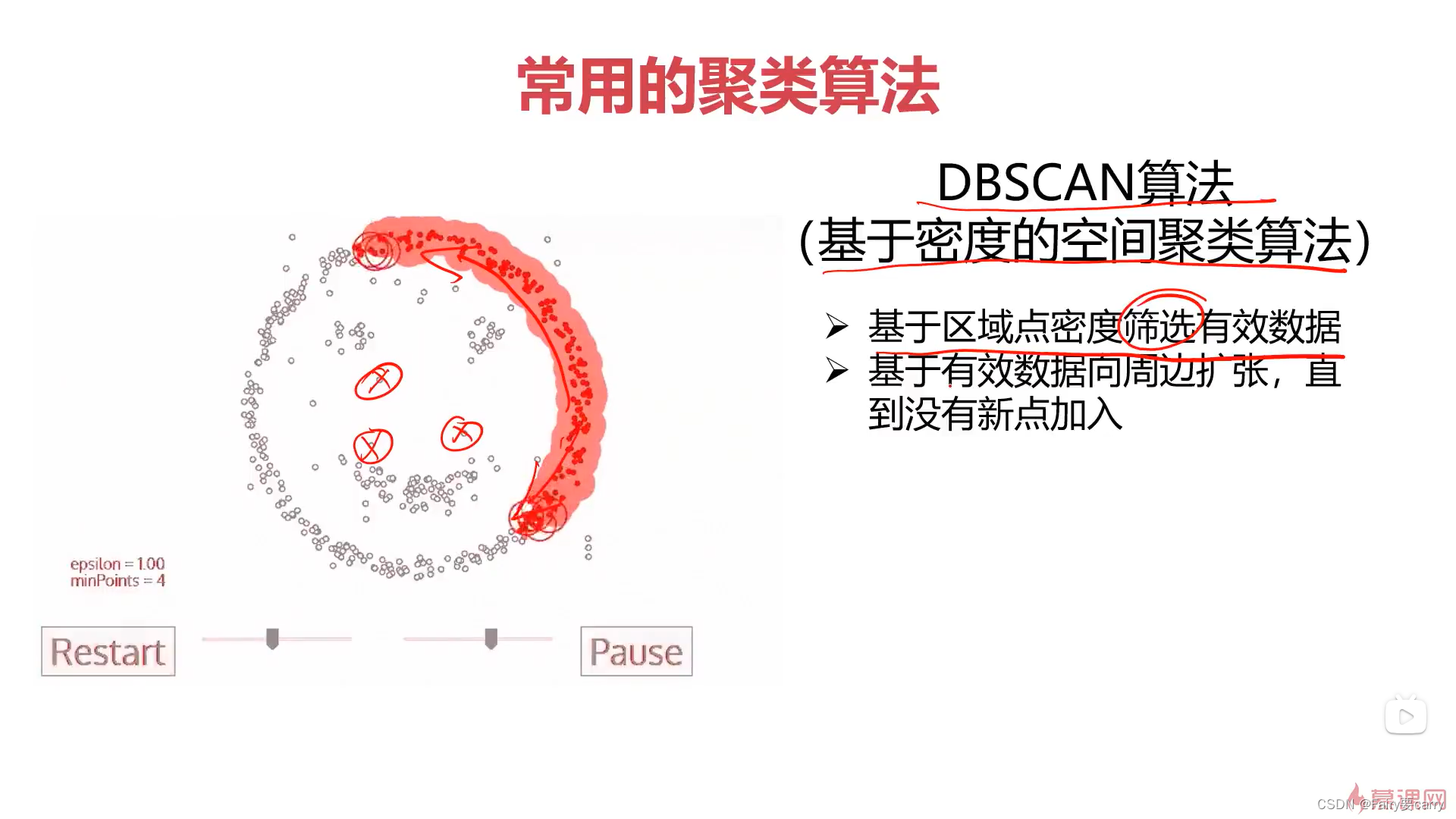
无监督式学习
1.是什么? 无监督式学习与监督式学习**最大的区别就是:**没有事先给定的训练实例,它是自动对输入的示例进行分类或者分群; 优点:不需要标签数据,极大程度上扩大了我们的数据样本,其次不受监督信…...

docker 安装镜像及使用命令
目录 1. Mysql2. Redis3. Nginx4. Elasticsearch官网指导 docker pull 容器名:版本号 拉取容器, 不指定版本号默认最新的 run 运行 -d 后台运行 -p 3306:3306 -p是port 对外端口:对内端口 –name xyy_mysql 容器名称 -e MYSQL_ROOT_PASSWORD123456 环境变量 -v 系统地址:docker…...

Python运维之多进程!!
本节的快速导航目录如下喔!!! 一、创建进程的类Process 二、进程并发控制之Semaphore 三、进程同步之Lock 四、进程同步之Event 五、进程优先队列Queue 六、多进程之进程池Pool 七、多进程之数据交换Pipe 一、创建进程的类Process mu…...

Redis(无中心化集群搭建)
文章目录 1.无中心化集群1.基本介绍2.集群说明 2.基本环境搭建1.部署规划(6台服务器)2.首先删除上次的rdb和aof文件(对之前的三台服务器都操作)1.首先分别登录命令行,关闭redis2.清除/root/下的rdb和aof文件3.把上次的…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...
