关于实体类注解@Data、@EqualsAndHashCode(callSuper = true)、@Accessors(chain = true)的作用
笔记：都是lombook插件的注解，作用是简化优化代码等，比如getter、setter，一般三者连用能避免一些如继承类的导致的一些坑，比如equal()方法的错误，具体用法可查阅每个注解及属性的作用。
@Accessors(chain = true)一般用于配置getter和setter方法的生成结果，跟@Data套用，@Data也可用@getter@setter替代，这种方式来避免继承类的错误，也可以用@EqualsAndHashCode(callSuper = true)来重写equal()方法来避免
相关文章：
、@Accessors(chain = true)的作用)
关于实体类注解@Data、@EqualsAndHashCode(callSuper = true)、@Accessors(chain = true)的作用
笔记：都是lombook插件的注解，作用是简化优化代码等，比如getter、setter，一般三者连用能避免一些如继承类的导致的一些坑，比如equal()方法的错误，具体用法可查阅每个注解及属性的作用。 Accessors(chain tr…...
5.9号模拟前端面试10问
5.9号模拟前端面试10问 1.html语义化的理解 HTML语义化是指使用具有明确含义的HTML标签来描述内容，而不仅仅是使用<div>和<span>等通用容器标签。语义化的HTML代码更易于阅读和维护，同时也有助于搜索引擎优化（SEO）。…...
vue3 JSX的使用与警告【JSX 元素隐式具有类型 “any“，因为不存在接口 “JSX.IntrinsicElements“】解决办法
一、安装 pnpm i vitejs/plugin-vue-jsx -D 二、配置 1、tsconfig.json "compilerOptions":{"jsx":"preserve" } 2、vite.config.ts import VueJsx from "vitejs/plugin-vue-jsx"...plugin:[vue(),VueJsx() ] 三、简单使用案例…...
一、计算机基础(Java零基础一)
🌻🌻目录 一、🌻🌻剖析学习Java前的疑问🌻🌻1.1 零基础学习编程1.2 英语不好能学吗？1.3 理解慢能学好吗？1.4 现在学Java晚吗？1.5 Java 和 Python 还有 Go 的选择1.6 Java…...
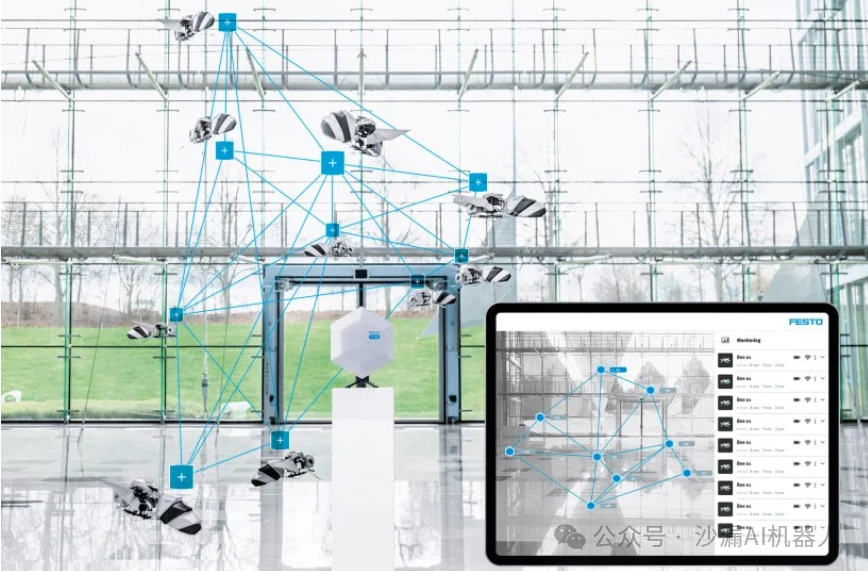
德国著名自动化公司Festo设计了一款仿生蜜蜂，仅重34g，支持多只蜜蜂编队飞行！...
德国著名的气动元件研发及自动化解决方案供应商Festo公司近日展示了一款仿生蜜蜂（BionicBee），重量只有34g，却完全可以实现自主飞行，还支持多只相同的蜜蜂机器人编队飞行。 BionicBee 重约 34 克，长 22 厘米…...
折腾记：C++用开源库Snap7通过S7协议连接西门子PLC
初级代码游戏的专栏介绍与文章目录-CSDN博客 我的github：codetoys，所有代码都将会位于ctfc库中。已经放入库中我会指出在库中的位置。 这些代码大部分以Linux为目标但部分代码是纯C的，可以在任何平台上使用。 不是教程，是避坑指…...
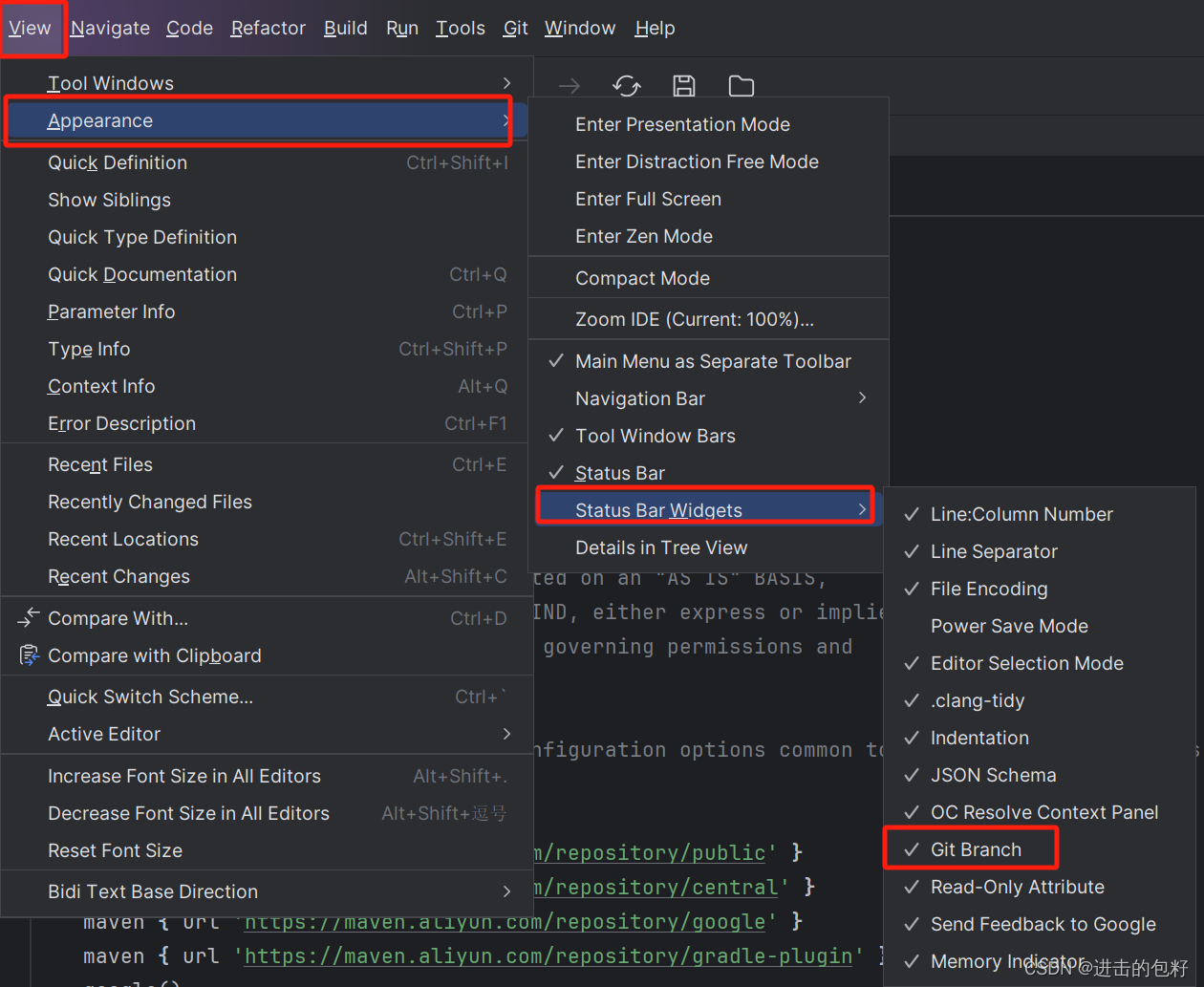
Android studio 新版本 NewUI toolbar显示快捷按钮
新版本的Android studio 启用新的界面，以前许多快捷按键位置有变化 文章目录 设置始终显示主菜单设置ToolBar快捷按钮显示设置右下角显示分支 设置始终显示主菜单 原本要点击左上角几个横向才显示的菜单 设置始终显示，View -> Appearance -> Mai…...
辛普森公式求函数的近似积分【通用计算】
利用辛普森公式可以近似求出复杂函数的积分值，公式如下： ∫ a b f ( x ) d x ≈ h 3 [ y 0 y 2 n − 1 4 ( ∑ i 1 n − 1 y 2 i − 1 ) ∑ i 1 n − 1 y 2 i ] \int_{a}^{b} f(x) dx \approx \frac{h}{3}\left[ y_0 y_{2n-1} 4(\sum\limits_{i1…...
即插即用 | YOLOv8热力图可视化方法详解，揭秘AI如何「看」世界！【附完整源码】
《博主简介》 小伙伴们好，我是阿旭。专注于人工智能、AIGC、python、计算机视觉相关分享研究。 ✌更多学习资源，可关注公-仲-hao:【阿旭算法与机器学习】，共同学习交流~ 👍感谢小伙伴们点赞、关注！ 《------往期经典推…...
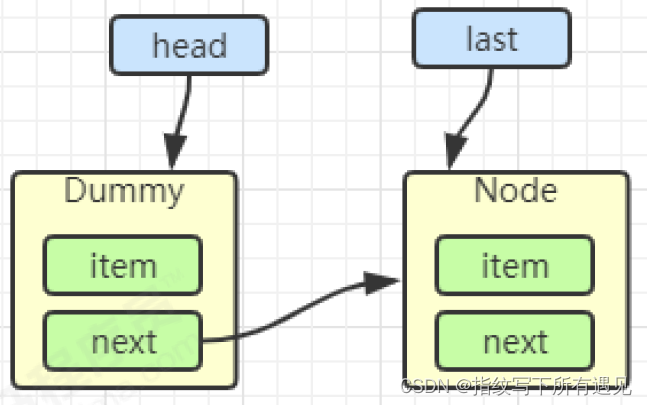
多线程学习D10 收尾了应该
线程安全集合类概述 重点介绍java.util.concurrent.* 下的线程安全集合类，可以发现它们有规律，里面包含三类关键词：Blocking、CopyOnWrite、Concurrent Blocking 大部分实现基于锁，并提供用来阻塞的方法 CopyOnWrite 之类容器修改…...
ai可以做思维导图吗？当然是可以的！
ai可以做思维导图吗？在快节奏的现代生活中，思维导图作为一种高效的信息组织和表达工具，越来越受到人们的青睐。随着人工智能（AI）技术的不断发展，AI思维导图软件也应运而生，它们不仅能够帮助用户…...
景源畅信数字：抖音小店的入住门槛大不大？
近年来，随着短视频平台的崛起，抖音小店逐渐成为了众多商家和创业者关注的焦点。那么，抖音小店的入住门槛究竟大不大呢?本文将从四个方面对这一问题进行详细阐述。 一、注册流程 抖音小店的注册流程相对简单，只需按照官方指引完成…...
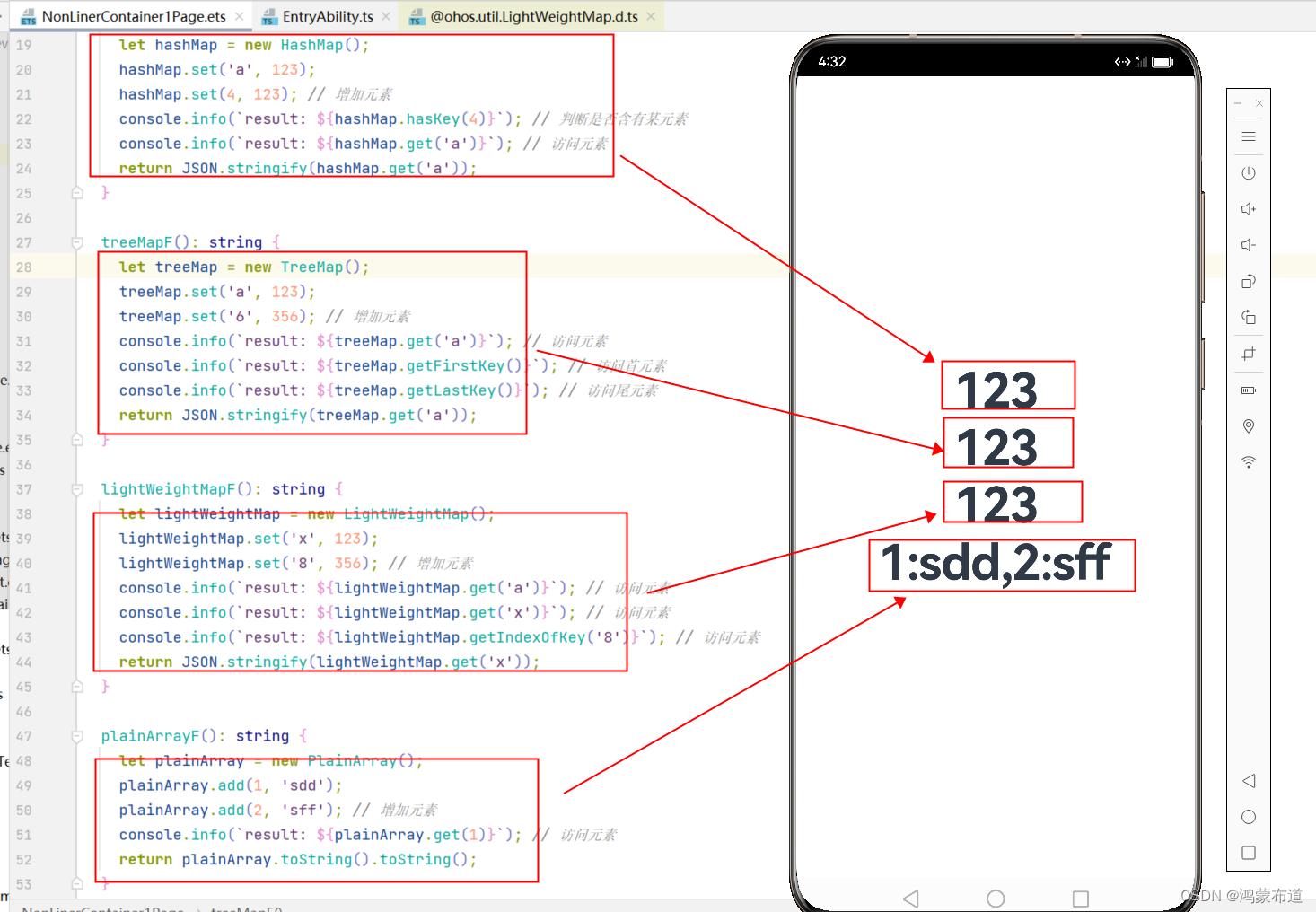
鸿蒙开发-ArkTS语言-容器-非线性容器
鸿蒙开发-UI-web 鸿蒙开发-UI-web-页面 鸿蒙开发-ArkTS语言-基础类库 鸿蒙开发-ArkTS语言-并发 鸿蒙开发-ArkTS语言-并发-案例 鸿蒙开发-ArkTS语言-容器 文章目录 前言 一、非线性容器 1.HashMap 2.HashSet 3.TreeMap 4.TreeSet 5.LightWeightMap 6.LightWeightSet 7.P…...
【C语言】指针篇- 深度解析Sizeof和Strlen：热门面试题探究（5/5)
🌈个人主页：是店小二呀 🌈C语言笔记专栏：C语言笔记 🌈C笔记专栏： C笔记 🌈喜欢的诗句:无人扶我青云志 我自踏雪至山巅 文章目录 一、简单介绍Sizeof和Strlen1.1 Sizeof1.2 Strlen函数1.3 Sie…...
【设计模式】单例模式的前世今生
文章目录 引言简介起航！向“确保某个类在系统中只有一个实例”进发 ⛵️Lazy SingletonDouble-checked locking（DCL） SingletonVolatile SingletonAtomic SingletonMeyers Singleton 附：C静态对象的初始化 引言 说起单例模式&…...
厦门网上在线教育系统,线下老师怎么转型到线上网上授课？
现在很多 线下老师都想转到线上做网课，但是在转线上过程中会出现很多问题，很多人都不知道怎么开始，今天小编和大家说一下要注意的。 一、你要有一套适合线上的教学视频 首先你要准备做的课程内容是什么，怎么讲，讲什么&…...
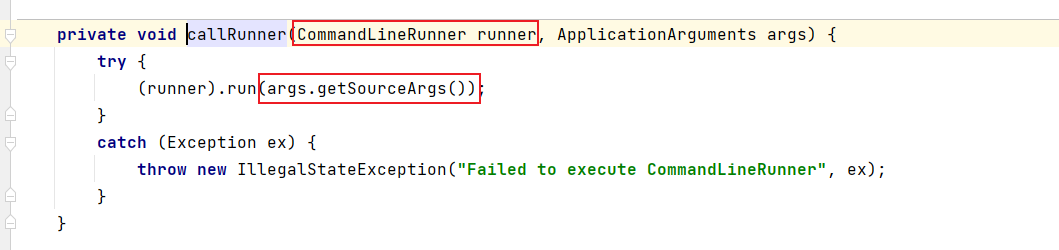
Spring底层入门（九）
boot的执行流程分为构造SpringApplication对象、调用run方法两部分 1、Spring Boot 执行流程-构造 通常我们会在SpringBoot的主启动类中写以下的代码： 参数一是当前类的字节码，参数二是main的args参数。 public class StartApplication {public static…...
掌握Android Fragment开发之魂：Fragment的深度解析（下）
在上一篇文章中，我们深入探讨了Fragment 通信，包含Fragment 向 Activity 传递数据、Activity 向 Fragment 传递数据、Fragment 之间的通信方式。感兴趣的朋友，请前往查阅： 掌握Android Fragment开发之魂：Fragment的深度…...
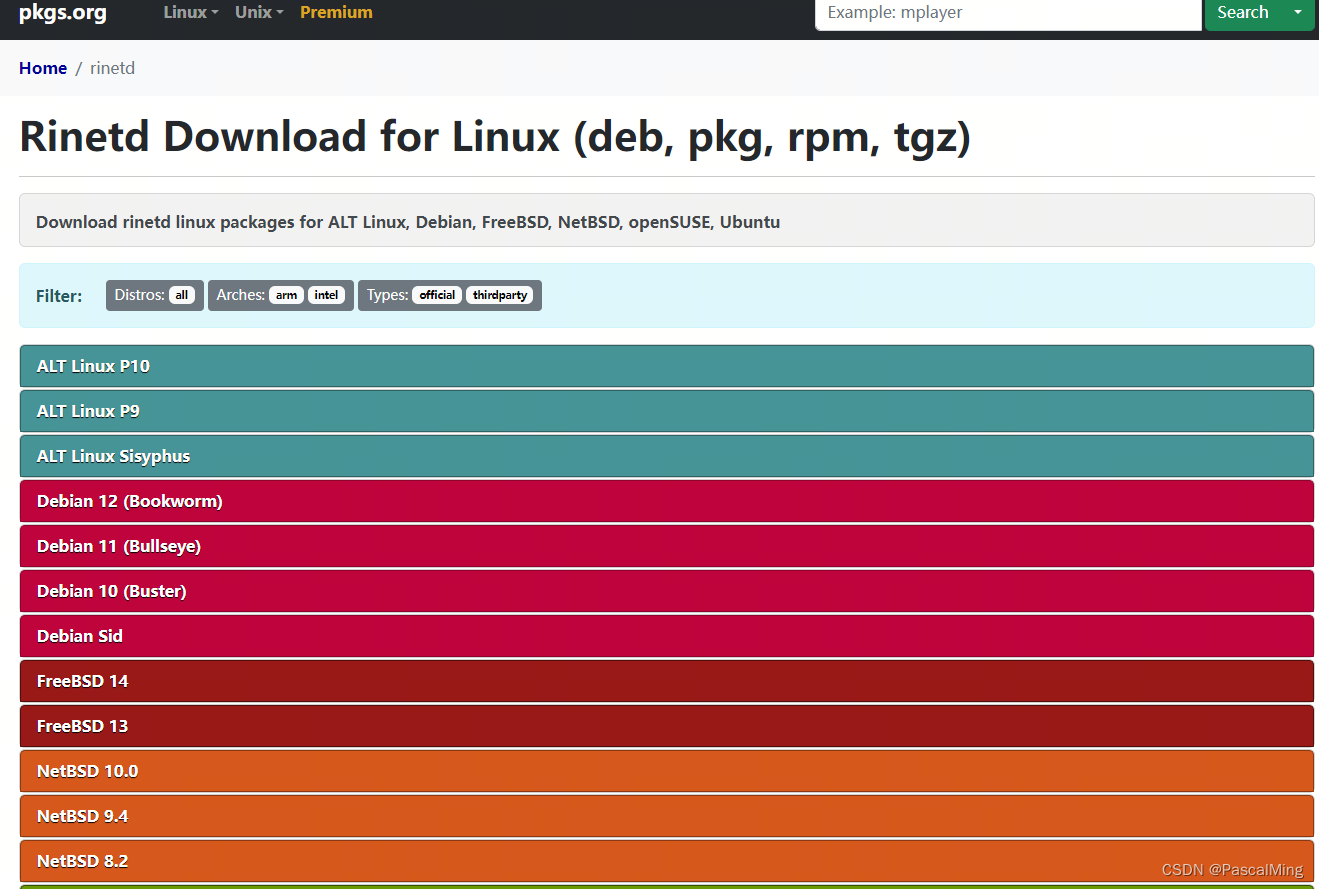
小巧简单实用的Linux端口转发工具Rinetd
Linux下实现端口转发有很多种方法，尤其是在可以联网的情况下，更是容易。最近在资源受限的定制系统中，找到一个方便离线安装和使用的端口转发工具Rinetd，安装包仅几十K，而且有很多版本的Linux发行系统的支持。 1、安装…...
HackBar 新手使用教程(入门)
啥是Hackbar？ Hackbar是一个Firefox 的插件,它的功能类似于地址栏,但是它里面的数据不受服务器的相应触发的重定向等其它变化的影响。 有网址的载入于访问,联合查询,各种编码,数据加密功能。 这个Hackbar可以帮助你在测试SQL注入,XSS漏洞和网站的安全性,主要是帮助…...
Lombok 的 @Data 注解失效，未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误，它们的含义、原因和解决方法都有显著区别。以下是详细对比： 1. HTTP 406 (Not Acceptable) 含义： 客户端请求的内容类型与服务器支持的内容类型不匹…...
K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作： 1）、切换集群 2）、切换节点 3）、切换到 apparmor 的目录 4）、执行 apparmor 策略模块 5）、修改 pod 文件 6）、…...
【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成：MAC头部frame bodyFCS，其中MAC是固定格式的，frame body是可变长度。 MAC头部有frame control，duration，address1，address2，addre…...
以下是对华为 HarmonyOS NETX 5属性动画（ArkTS）文档的结构化整理，通过层级标题、表格和代码块提升可读性：
一、属性动画概述NETX 作用：实现组件通用属性的渐变过渡效果，提升用户体验。支持属性：width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项： 布局类属性（如宽高）变化时&#…...
mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程，并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令，把数据流转换成Message，状态转变流程是：State::Created 》 St…...
OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成，核心是利用 HTTP 协议的 Range 请求头指定下载范围： 实现原理 Range 请求头：向服务器请求文件的特定字节范围（如 Range: bytes1024-） 本地文件记录：保存已…...
第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用，通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试，通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...
DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API，查询的是单条数据，比如根据主键ID查询用户信息，sql如下： select id, name, age from user where id #{id}API默认返回的数据格式是多条的，如下： {&qu…...
HTML前端开发：JavaScript 常用事件详解
作为前端开发的核心，JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例： 1. onclick - 点击事件 当元素被单击时触发（左键点击） button.onclick function() {alert("按钮被点击了！&…...
基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码，实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...